FIR 전송 함수

전달함수 필터는 전달함수와 Convolution 정리를 이용하여 필터를 생성한다.본 기사에서는 유한 임펄스 응답을 이용한 필터의 예를 설명하고 실제 데이터로의 필터 적용을 제시한다.

FIR(Finite Impulse Response) 선형 필터

디지털 처리에서 FIR 필터는 시간에 따라 변하지 않는 시간 연속 필터입니다.즉, 필터는 특정 시점에 따라 달라지는 것이 아니라 시간에 따라 달라집니다.이 필터의 사양은 입력의 원하는 주파수만 통과하는 주파수 응답을 갖는 전송 함수를 사용합니다.이 유형의 필터는 비재귀적입니다.즉, 출력의 재귀 값 없이 입력 조합에서 출력을 완전히 도출할 수 있습니다.즉, 이전 출력의 값을 새 출력에 공급하는 피드백 루프가 없습니다.이는 위상 ^[1]왜곡 없이 입력을 통과하기 때문에 선형 위상 응답을 필요로 하는 응용 프로그램에서 IIR 필터(Infinite Impulse Response)와 같은 재귀 필터보다 유리합니다.

수학적 모형

출력 함수를 $y(t)$ ) { $displaystyle$ y $(t)},$ 입력을 $y(t)$ $x(t)$ $)$ { $displaystyle$ x $(t$ 로 합니다.전송 $h(t)$ h ( $h(t)$ ) { $displaystyle$ h $(t)}$ 를 $h(t)$ 사용한 입력의 회전은 필터링된 출력을 제공합니다.이 필터 유형의 수학적 모델은 다음과 같습니다.

y(t)=\int _{0}^{T}x(t-\tau),h(\display),d\display

$(\displaystyle\displaystyle$ 는 입력에 대한 임펄스 응답 전송 함수입니다.컨볼루션에서는 입력이 동일한 시간 값으로 신호를 기록한 경우에만 필터를 활성화할 수 있습니다.이 필터는 k가 함수 h의 지원 영역에 속할 경우 입력 값(x(t))을 반환합니다.이것이 이 필터를 유한 응답이라고 하는 이유입니다.k가 지원 영역 밖에 있는 경우 임펄스 응답은 0이 되어 출력이 0이 됩니다. $\tau$ h $(\displaystyle\tau$ 함수의 중심 개념은 두 ^[2]함수의 몫으로 생각할 수 있습니다.

Huang(1981)^[3]에 따르면 이 수학적 모델을 사용하여 다양한 동시 필터 설계를 사용하여 비재귀 선형 필터를 설계하는 방법은 네 가지가 있습니다.

창호 설계 방법
주파수 샘플링 방법
기존 선형 프로그래밍
반복 선형 프로그래밍

단면 선형 필터

입력 함수

입력 신호를 정의합니다.

({displaystyle y(t)=\sin(t)+randword{bmatrix}1&200\end{bmatrix}})

$rand({\begin{bmatrix}1&200\end{bmatrix}})$ $rand({\begin{bmatrix}1&200\end{bmatrix}})$ $rand({\begin{bmatrix}1&200\end{bmatrix}})$ d ( $rand({\begin{bmatrix}1&200\end{bmatrix}})$ [ $]$ ){ $display style$ rand \ \ display { $bmatrix }$ 1 $rand({\begin{bmatrix}1&200\end{bmatrix}})$ & $200 \ end$ { $bmatrix$ }} $rand({\begin{bmatrix}1&200\end{bmatrix}})$ 、 데이터를 왜곡하는 사인파 함수에 1 ~200의 난수를 추가합니다.

단측 필터

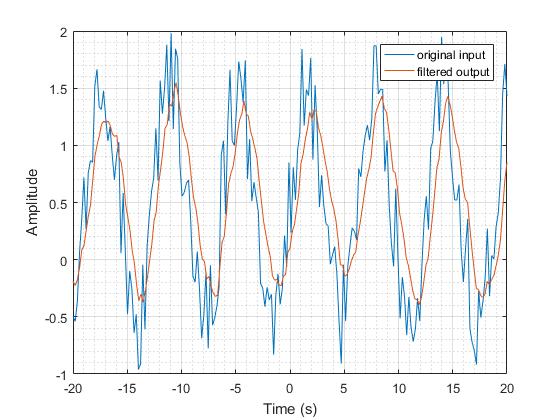
양수 값의 지지 영역에 대한 임펄스 응답으로 지수 함수를 사용합니다.

h(t)=cases}0,\forall &-infty &\leq 0\e^{-t},\forall &\leq &\leq +\infty \end{cases}

이 필터의 주파수 응답은 저주파수 필터와 유사합니다.

양면 필터

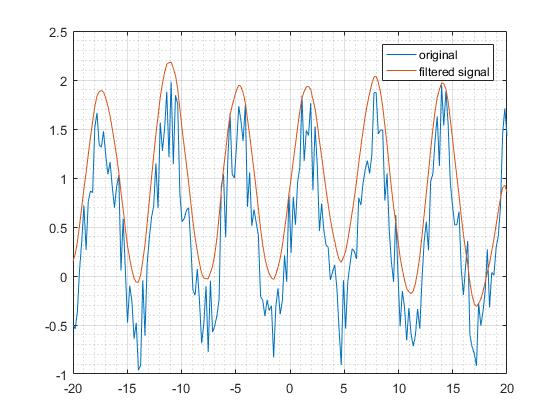
입력 신호를 단측 함수와 동일하게 합니다.이전과 같이 양수 값의 지지 영역에 대한 임펄스 응답으로 지수 함수를 사용합니다.이 양면 필터에서는 다른 지수함수도 구현합니다.지수의 거듭제곱의 신호에서 그 반대는 지수함수를 계산할 때 무한하지 않은 결과를 유지하는 것입니다.

$h(t)=cases}e^{t},\forall &\leq &\leq 0\e^{-t},\forall &\leq &\leq +\infty \end{cases}}$

주파수 영역에서 이 필터를 조사하면 매그니튜드 응답은 싱글사이드 필터와 같은 경향을 보입니다.단, 통과할 수 있는 주파수는 단측 필터의 주파수보다 작습니다.이것에 의해, 출력이 부드러워졌습니다.이 결과의 중요한 점은 선형 필터의 양면 필터 유형이 필터가 되는 것이 더 좋다는 것입니다.