무한 임펄스 응답

이 기사는 어떠한 출처도 인용하지 않는다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : '무한 임펄스 응답'– 뉴스 · 신문 · 서적 · 학자 · JSTOR (2015년 4월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인)

무한 임펄스 응답(IIR)은 임펄스 $응답h{\displaystyle }$(${\displaystyle }$t $)\displaystyle$ h$(t)$를 가지는 것으로 구별되는 많은 선형 시간 불변 시스템에 적용되는 속성입니다.이 응답은 특정 포인트를 지나도 정확히0이 되지 않고 무한히 계속됩니다.이는 유한 임펄스 응답(FIR) 시스템과는 대조적으로 임펄스 응답은 일부 $유한{\displaystyle }$T(\$displaystyle$ T$)$에 대해 $>$ T(\$displaystyle T>$T)의 시간에 정확히0이 되어, 그 기간이 유한합니다.선형 시간 불변 시스템의 일반적인 예는 대부분의 전자 및 디지털 필터입니다.이 속성을 가진 시스템을 IIR 시스템 또는 IIR 필터라고 합니다.

실제로, IIR 시스템의 임펄스 응답은, 통상, 0에 가까워져, 특정의 포인트를 지나 방치될 가능성이 있습니다.그러나 IIR 또는 FIR의 반응을 일으키는 물리적 시스템은 서로 다르므로 그 구별의 중요성이 존재한다.예를 들어 저항기, 캐패시터 및/또는 인덕터(및 아마 선형 증폭기)로 구성된 아날로그 전자 필터는 일반적으로 IIR 필터입니다.한편, 피드백이 없는 탭 지연 회선에 근거하는 이산 시간 필터(통상은 디지털 필터)는 필연적으로 FIR 필터입니다.아날로그 필터의 캐패시터(또는 인덕터)는 "메모리"를 가지며, 그 내부 상태는 임펄스(양자 효과가 무시되는 캐패시터 및 인덕터의 고전적 모델)에 따라 완전히 완화되지 않습니다.단, 후자의 경우, 임펄스가 탭된 지연선의 끝에 도달한 후, 시스템은 그 임펄스에 대한 메모리를 더 이상 가지고 있지 않고 초기 상태로 돌아갑니다.그 포인트 이후의 임펄스 응답은 정확히0 입니다

구현 및 설계

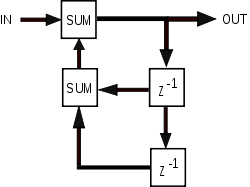
거의 모든 아날로그 전자 필터가 IIR이지만 디지털 필터는 IIR 또는 FIR일 수 있습니다.일반적으로 이산 시간 필터의 토폴로지에 피드백이 있으면(아래 블록 다이어그램 등) IIR 응답이 생성됩니다.IIR 필터의 z 도메인 전송 함수에는 이러한 피드백 용어를 설명하는 사소한 요소가 포함되어 있습니다.한편, FIR 필터의 전송 함수는, 다음에 나타내는 일반적인 형식과 같이, 분자만을 가지고 있습니다.i> { displaystyle i > $0$} (피드백 항)의 $i{\displaystyle {}_{}}${ $displaystyle$ $a_{i}$ 계수는$$ 모두 0이며 필터에는 유한 극이 없습니다.

IIR 아날로그 전자 필터와 관련된 전송 함수는 그 진폭과 위상 특성을 위해 광범위하게 연구되고 최적화되었습니다.이러한 연속 시간 필터 함수는 Laplace 도메인에 설명되어 있습니다.쌍선형 변환, 임펄스 불변성 또는 극 제로 매칭 방법과 같은 특정 수학적 기법을 사용하여 전달 함수가 z 영역에서 표현되는 이산 시간 필터의 경우에 원하는 솔루션을 전송할 수 있다.따라서 디지털 IIR 필터는 체비셰프 필터, 버터워스 필터 및 타원 필터와 같은 아날로그 필터에 대한 잘 알려진 솔루션을 기반으로 할 수 있으며 이러한 솔루션의 특성을 계승할 수 있습니다.

전달 함수 도출

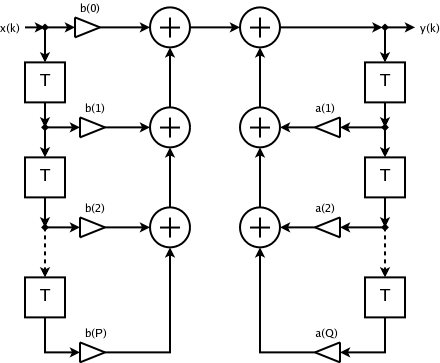
디지털 필터는 출력 신호가 입력 신호와 어떻게 관련되어 있는지를 정의하는 차분 방정식의 관점에서 설명 및 구현되는 경우가 많습니다.

${\displaystyle {n}y[n]={1}{a_{0}}(b_{0}x[n]+b_{1}x[n-1]+\cdots +b_{P}x[n-P]\&}-a_{1}y[2-2]$

여기서:

• $\displaystyle\P는$$$피드포워드 필터 순서입니다.
• ${\displaystyle b_{}}$ i$(\displaystyle\b_{$i$$})는 피드포워드 필터 계수입니다.
• $(\displaystyle\Q)$는 피드백 필터 순서입니다.
• $\$는 피드백 필터 계수입니다.
• ${\displaystyle x}$[ $]$ \ $displaystyle \x$[$n$]는$$ 입력 신호입니다.
• ${\displaystyle y}$[ $]$ \ $displaystyle \ y$ [ $n$]는$$ 출력 신호입니다.

차분 방정식의 보다 축약된 형식은 다음과 같습니다.

${\displaystyle \ y[n]= flac {1}{a_{0}}\left(\sum _ {i=0}^{P}b_{i}x[n-i]-\sum _ {j=1}^{Q}a_{j}y[n-j]\right)}$

재배열하면 다음과 같이 됩니다.

$\displaystyle \\sum _{j=0}^{Q}a_{j}y[n-j]=\sum _{i=0}^{P}b_{i}x[n-i]}$

필터의 전달 함수를 찾으려면 먼저 위 방정식의 각 변의 Z 변환을 취합니다. 여기서 시간 이동 특성을 사용하여 다음을 얻습니다.

${\displaystyle \\sum _{j=0}^{Q}a_{j}z^{-j}Y(z)=\sum _{i=0}^{P}b_{i}z^{-i}X(z)}$

전송 함수는 다음과 같이 정의됩니다.

$({displaystyle {begin{aligned}H(z)&=begin{i=0}^{P}b_{i}z^{-i}}{\sum_Q}a_{j}z^{-j}}{end}}}) 정렬됨$

대부분의 IIR 필터 설계에서 0$(\$의 ${\displaystyle 계수}$가 1임을 고려하면 IIR 필터 전송 함수는 보다 전통적인 형식을 취합니다.

${\displaystyle H(z)=brac {sum _{i=0}^{P}b_{i}z^{-i}}{1+\sum_{j=1}^{Q}a_{j}z^{-j}}$

안정성.

전송 함수를 사용하면 시스템이 bounded-input, bounded-output(BIBO; 경계입력, 경계출력) 안정 여부를 판단할 수 있습니다.구체적으로 말하면, BIBO 안정성 기준은 시스템의 ROC에 단위 원이 포함되도록 요구한다.예를 들어 원인 시스템의 경우 전달 함수의 모든 극은 1보다 작은 절대값을 가져야 합니다.즉, 모든 극은 $\displaystyle$z 평면의$$ 단위 원 안에 위치해야 합니다.

극은 H$)$의 분모를 0으로 만드는 z$(\$$displaystyle z) 값$으로 정의됩니다.

${\displaystyle\0=\sum_{j=0}^{Q}a_{j}z^{-j}$

${\displaystyle j_{}}$ ${\displaystyle 0}$0인 $경우$(\$style a_{$j}\$neq$ 0$$$)$ 극은 $(\displaystyle$ z$)$ 평면의$$ 원점에 위치하지 않습니다.이는 모든 극이 원점에 위치하는 FIR 필터와 대조적이며, 따라서 항상 안정적입니다.

IIR 필터는 같은 순서의 FIR 필터보다 훨씬 선명한 전이 영역의 롤오프를 실현할 수 있기 때문에 FIR 필터보다 IIR 필터가 우선되는 경우가 있습니다.

예

이산 시간 필터의 전달 $함수{\displaystyle }$H (${\displaystyle z}$) {$displaystyle$ H$(z)}$를 다음과 같이 설정합니다.

${\displaystyle H(z)=marchfrac {B(z)}{A(z)}}=marchfrac {1}{1-az^{-1}}}$

$파라미터{\displaystyle }$ a$(\displaystyle$ a$)$에 의해 제어됩니다.실수는 0< <\$displaystyle$0 <$a$ 1.H${\displaystyle }$$)\displaystyle$ H($z)\$$displaystyle$ a$\}$에서 안정적이고 인과관계가 있습니다.시간 도메인 임펄스 응답은 다음과 같이 표시됩니다.

${\displaystyle h(n)=a^{n}u(n)}$

$여기$서${\displaystyle }$u (${\displaystyle n}$ )$${$displaystyle$u($n)}$는 유닛 스텝 함수입니다.$h{\displaystyle }$(${\displaystyle n}$ )$${ $displaystyle$ h$(n)}$는 모든 n${\displaystyle }$≤$$0 { $displaystyle$ n$\geq$ 0$\}$에 대해 0이 아니므로 임펄스 응답은 무한히 계속됩니다.

장점과 단점

FIR 필터에 비해 디지털 IIR 필터의 주된 장점은 패스밴드, 스톱밴드, 리플 및/또는 롤오프에 관한 사양을 충족하기 위한 구현 효율입니다.이러한 사양의 세트는, 같은 요건을 만족시키는 FIR 필터에 필요한 것보다 낮은 순서(위의 공식에서는 Q)의 IIR 필터로 실현할 수 있습니다.신호 프로세서에 실장되어 있는 경우, 이것은 시간 스텝당 계산의 수가 그만큼 적다는 것을 의미합니다.대부분의 경우, 계산의 절약은 큰 요인이 됩니다.

한편, FIR 필터는, 예를 들면, 특정의 주파수 응답 요건에 맞추어 설계하기 쉬워집니다.아날로그 필터에 대해 연구 및 최적화되어 있는 일반적인 케이스(하이패스, 로우패스, 노치 등) 중 하나가 아닌 경우 특히 그렇습니다.또한 FIR 필터는 쉽게 선형 위상(그룹 지연과 주파수의 일정)으로 만들 수 있습니다.이것은 IIR 필터를 사용하면 쉽게 충족되지 않는 속성이며, 그 후에 근사치(베셀 필터 등)로서만 충족됩니다.디지털 IIR 필터에 관한 또 다른 문제는 양자화와 연계된 피드백 시스템 때문에 유휴 상태에서의 한계 주기 동작의 가능성입니다.

설계 방법

임펄스 불변성

임펄스 불변성은 연속시간 시스템의 임펄스 응답을 샘플링하여 이산시간 시스템의 임펄스 응답을 생성하는 연속시간 필터에서 이산시간 무한 임펄스 응답(IIR) 필터를 설계하는 기술입니다.임펄스 불변성은 s 평면에서 z 평면으로 매핑하는 두 가지 기본 요구 사항을 충족하기 위해 일반적으로 사용되는 방법 중 하나입니다.이는 아날로그 필터와 동일한 샘플링 시간에 동일한 출력 값을 갖는 T(z)를 해결함으로써 얻을 수 있으며 입력이 펄스 내에 있을 때만 적용됩니다.
이 방법으로 생성되는 디지털 필터의 모든 입력은 매우 정확한 펄스 입력을 제외하고 대략적인 값입니다.이것은 가장 간단한 IIR 필터 설계 방식입니다.저주파수에서 가장 정확하기 때문에 보통 저역 통과 필터에 사용됩니다.

Laplace 변환 또는 z 변환의 경우 변환 후의 출력은 입력에 해당하는 변환 함수 T(s) 또는 T(z)를 곱한 값일 뿐입니다.Y(s) 및 Y(z)는 각각 입력 X(s) 및 입력 X(z)의 변환 출력입니다.

${\displaystyle Y(s)=T(s)X(s)}$

${\displaystyle Y(z)=T(z)X(z)}$

단위 임펄스에 라플라스 변환 또는 z 변환을 적용하면 결과는 1입니다.따라서 변환 후의 출력 결과는 다음과 같습니다.

${\displaystyle Y(s)=T(s)}$

${\displaystyle Y(z)=T(z)}$

아날로그 필터의 출력은 시간 영역의 역라플라스 변환에 불과합니다.

${\displaystyle y(t)=L^{-1}[Y(s)]= L^{-1}[T(s)]}$

t 대신 nT를 사용하면 샘플링 시 펄스로부터 파생된 출력 y(nT)를 얻을 수 있습니다.그것은 또한 y(n)로써 표현할 수 있다

${\displaystyle y(n)=y(nT)=y(t)_{t=sT}}$

이 이산 시간 신호 T(z)을 얻기 위해 z-transform 적용될 수 있다.

${Tᆩ=Yᆪ=Z[y(nx]\displaystyle}$

${Tᆪ=Z[y(nx]=Z[y(nT)]\displaystyle}$

${\displaystyle T(z)=Z\left\{L^{)}[T(s)]_{t=nT}\right\}}$

마지막 방정식 수학적으로는 디지털 imaging필터고 T(s)로 라플라스, 이는 보통화되는 문제에 의해 부분 이용되고 있는 아날로그 신호에 z-transform을 하는 것이다에 대해 설명합니다.

${\displaystyle Tᆩ=Z[T(s)]*T}$

사실 승산기 T는 공식으로 출연하고 있다에 유의하십시오.하더라도 단위 펄스의 라플라스 변환과 z-transform 1호이다. 왜냐하면, 그 펄스가 반드시 똑같다.아날로그 신호의 경우, 펄스지만 지역이 1t=0에, 그러나 그것은 1discrete-time 펄스 t=0에서 승수 T의 존재 필요하다 그래서 무한 가치를 가지고 있습니다.

스텝 불변성

충격 invariant보다 단계 불변성은 좋은 설계 방법이다.그 디지털 필터 다른 상수를 입력의 여러 부분들을 가지고 있는 불연속 단계로 구성되어 있을 때 채취.이번 조치로 고정 imaging필터 덜 ADC에 동일한 입력 step신호보다 정확하다.단, 임펄스 불변량보다 입력에 더 적합합니다.
스텝 불변성은 T(z)와 T(s)가 모두 스텝 입력일 때 동일한 샘플 값의 문제를 해결합니다.디지털 필터에 대한 입력은 u(n)이고 아날로그 필터에 대한 입력은 u(t)입니다.이 두 입력에 z-변환 및 Laplace 변환을 적용하여 변환된 출력 신호를 얻습니다.
${\displaystyle \mathrm{스텝}}$ $입력{\displaystyle }$ Z${\displaystyle }$[${\displaystyle u}$(${\displaystyle }$n ) ${\displaystyle ={\displaystyle \frac{z}{}}}$- ${\displaystyle {\displaystyle \frac{1}{}}}$ { $displaystyle Z [$u$$( n ) ] =$specdfrac {z}$ {$z-1}$ 을 실행합니다.
$z-timeout{\displaystyle }$ Y (${\displaystyle z}$ )${\displaystyle =T}$ (${\displaystyle z}$ )${\displaystyle U}$ (${\displaystyle z}$ ) $=$ (${\displaystyle z}$ ) ${\displaystyle {\displaystyle \frac{z}{}}}$z -$$ { $display$Y ( z ) =$T$( $z$) { \$dfrac$ { z } }$$z z z z z 。
${\displaystyle \mathrm{스텝}}$ $입력{\displaystyle }$L [${\displaystyle u}$( t )${\displaystyle }$]$=$ ${\displaystyle 1{\displaystyle \frac{\mathrm{}}{}}}$ { $displaystyle$L [$u$ ( t) ]= laplace $dfrac${1} {$s}}$ 에 대해 Laplace 변환을 수행합니다.
Laplace $변환{\displaystyle }$후 변환된 출력 Y (${\displaystyle s}$ ) ${\displaystyle =T}$ (${\displaystyle s}$ )${\displaystyle ={\displaystyle \frac{}{}}T{\displaystyle \frac{}{}}}$ (${\displaystyle {\displaystyle \frac{s}{}}}$ )$$ ( \ $displaystyle$Y ( s ) =$T$( s )$U$ ( s ) = scs $dfrac { T$ ( s )$$}
아날로그 필터의 출력은 Y(t)의 역라플라스 변환입니다.T초마다 샘플링되는 경우 Y(n)가 됩니다.Y(z)의 역변환입니다.이러한 신호는 디지털 필터와 아날로그 필터를 해결하는 데 사용되며 샘플링 시 동일한 출력을 가집니다.
다음 방정식은 아날로그 필터의 근사 공식인 T(z)의 해를 나타냅니다.

${\displaystyle T(z)=syslogdfrac {z-1}{z}}Y(z)}$

${\displaystyle T(z)=syslogdfrac {z-1}{z}Z[y(n)]}$

${\displaystyle T(z)=blockdfrac {z-1}{z}Z[Y(s)]$

${\displaystyle T(z)=syslogdfrac {z-1}{z}}Z[{\dfrac {T(s)}{s}}}}$

쌍선형 변환

쌍선형 변환은 컨포멀 매핑의 특수한 경우로, 연속 시간 영역(아날로그 필터라고도 함)에 있는 선형 시간 불변(LTI) 필터의 전송 $함수{\displaystyle {}_{}}$ H${\displaystyle {}_{}{a}_{}}$${\displaystyle {}_{}}$(${\displaystyle s}$ )$${ $display style$ H_${a$$}$ ($s$)를 선형 변환하는$$ 데 자주 사용됩니다$.$리앙트 필터가 사용됩니다.이중 선형 변환은 z 평면을 s 평면에 정확하게 매핑하는 자연 로그 함수의 1차 근사치입니다.라플라스 변환이 이산 시간 신호(해당 지연 단위 임펄스에 연결된 이산 시간 시퀀스의 각 요소를 포함)에 대해 수행될 때, 결과는 정확히 다음 치환과 함께 이산 시간 시퀀스의 Z 변환입니다.

$(\displaystyle\displaystyle\aligned\z&=e^s)T}\\&=sfrac {e^{sT/2}}{e^{-sT/2}\&\about {1+sT/2}{1-sT/2}\end{aligned}}$

$여기$서 T$${\$displaystyle$ T$}$는 쌍선형 변환 도출에 사용되는 사다리꼴 규칙의 수치 적분 단계 크기, 즉 샘플링 주기입니다.위의 쌍선형 근사치는 s$${\$displaystyle$ s$}$에 대해 해결할 수 있으며 s$=$( ${\displaystyle 1}$/ ${\displaystyle T}$ ) ${\displaystyle \ln }$( ($$z ) {$displaystyle$ s=(1$/T)\ln(z)}$에 $대해서도{\displaystyle }$ 유사한 근사치를 수행할 수 있습니다.

이 매핑의 역수(및 1차 쌍선형 근사치)는 다음과 같다.

${\displaystyle {\displaystyle}s&=svsfrac {1}{displaystyle}T}}\ln(z)\\ & = specfrac {2} {T}}\left[{\frac {z-1}{z+1}}+{\frac {1}{3}\left({\frac {z+1}}\right)^3}+{\frac {1}{5}\left({\frac {z-1}{z+1}}\right)^{5}+{frac}{frac}{7}{frac}{frac}}}{frac} {1}\frac} {frac} {frac} {frac}\&\약 {frac}{T}}{\frac {z-1}{z+1}}\&=frac {2}{T}}{\frac {1-z^{-1}}{1+z^{-1}}\end {aligned}}}$

이 관계는 아날로그 필터 또는 아날로그 필터의 디지털 무한 임펄스 응답(IIR) 필터 T(z)의 라플라스 전송 함수에서 사용됩니다.
쌍선형 변환은 기본적으로 이 1차 근사치를 사용하며 연속 시간 전달 $함수$인 ${\displaystyle H_{}}$ a${\displaystyle {}_{}}$(${\displaystyle }$s $)\displaystyle$H_${a$}($s)$로 대체합니다.

${\displaystyle s\왼쪽 화살표}{frac {2}{T}}{\frac {z-1}{z+1}}.}$

그것은

${\displaystyle H_{d}(z)=H_{a}(s){\bigg }_{s=blac{2}{T}}{\frac {z-1}{z+1}}=H_{a}\left({\frac {2}{T}}{\frac {z-1}{z+1}}\right.\ }$

IIR 디지털필터를 계산하는 데 사용되며 아날로그 필터의 라플라스 전송 함수에서 시작합니다.

「 」를 참조해 주세요.

• 자기 회귀 모형
• 전자 필터
• 유한 임펄스 응답
• 반복 관계, 수학적 공식화
• 시스템 분석

외부 링크

• Wayback Machine에서의 BOES 신호처리 DSP 코스 - DSP 입문]의 다섯 번째 모듈(2016년 7월 2일 아카이브 완료)
• IIR Digital Filter Design 애플릿 at the Wayback Machine (2010년 2월 13일 아카이브 완료)
• IIR 디지털 필터 설계 도구 - 계수, 그래프, 극, 0 및 C 코드를 생성합니다.
• 엔지니어JS Online IIR 설계 도구 - Java 필요