흐름도

Flow map
1812년 프랑스의 러시아 침공 찰스 조셉 미나드 지도

플로우 맵은 움직임을 나타내기 위해 선형 기호를 사용하는 테마 맵의 일종이다. 따라서 지도와 흐름도의 혼합으로 간주될 수 있다. 지도화 되고 있는 운동은 사람, 고속도로 교통, 무역 상품, 물, 아이디어 또는 심지어 통신 데이터를 포함한 모든 것들의 그것일 수 있다.[1] 움직이는 재료의 다양성, 그리고 그것들이 움직이는 것을 통한 지리적 네트워크의 다양성은 많은 다른 설계 전략으로 이어졌다. 일부 지도 제작자들은 이 용어를 선형 네트워크의 어떤 주제 지도까지 확장한 반면, 다른 사람들은 어떤 종류의 움직임을 구체적으로 보여주는 지도에 그것의 사용을 제한한다.

많은 플로우 맵은 흐름의 양에 비례하는 선폭을 사용하므로, 카토그램(지역변경), 비례점 기호 등 비례 크기를 사용하는 다른 맵과 유사하다.

역사

1838년 아일랜드의 철도 전 화물 교통 지도는 비례 상징을 사용한 최초의 주제 지도 중 하나이다.

흐름의 양을 시각적으로 나타내기 위해 가장 일찍 알려진 지도는 엔지니어 헨리 드루리 하네스(Henry Druri Hasnes)가 1838년에 아일랜드의 철도 건설 잠재력에 관한 보고서의 일부로 발행한 두 개의 지도로, 도로와 운하별 화물 수송량을 보여준다.[2][3] 그 후 몇 년 동안, 다른 사람들은 찰스 조셉 미너드에 의해 숙달될 때까지 유럽에서 이 기술을 실험했다.[4]

1850년대와 1860년대 동안, 미나드는 그의 수레 조각상들 사이에서 매우 다양한 주제에 대한 42개의 흐름 지도를 출판했다. 이 중에는 1812~1813년 그가 그린 1869년도의 프랑스 러시아 침공 지도도 있는데, 이 지도는 "역대 그린 통계그래픽 중 최고"라고 불리고 있다.[5][6] Minard의 많은 지도들은 컴퓨터 그래픽 시대에도 아직 개선되지 않은 디자인 기법을 사용한다.

1980년대에 월도 토블러는 컴퓨터로 플로우 맵을 만드는 실험을 했다.[7][8] 초기 컴퓨터 생성 맵은 마이너드 표준에 미치지 못했으나, 지오그래픽 정보 시스템(GIS)과 그래픽 소프트웨어는 플로우 맵 설계 능력이 향상되었다.

흐름 현상

1830년대 이후 다양한 흐름 지도가 만들어지면서 여러 형태로 움직임을 보여주고 있다. Eduard Imhof에 따르면, 흐름 지도는 움직이는 현상과 그것들이 움직이는 네트워크의 몇 가지 다른 측면을 나타낼 수 있다; 그는 다음을 열거했다.[9]: 94–95

  • 출발지와 목적지 : "어디서, 어디서부터 어디로 무엇인가 움직이는가?"
  • 경로: "어느 선으로 이동하십니까?" 이것은 정밀하게, 일반화하거나 직선의[10] 도식적인 형태로만 나타낼 수 있다.
  • 이동 유형: "무엇이 이동되었는가?" 이 명목 범주는 한 지점에서 다른 지점으로 제품이 운송되는 것, 운송 수단 또는 해류의 수온과 같은 변수를 포함할 수 있다.
  • 이동량: "얼마나 이동했는가? 운송되는 물품의 수량이 (단계적으로) 꾸준히 변화하고 있는가, 단계별로 변화하고 있는가?" 이는 하루 차량, 총 이주민 수, 초당 입방피트(입방피트)의 물 흐름과 같이 음이 아닌 비율 변수가 될 것이다. 일부 플로우 맵은 통신 대역폭과 같이 실제 이동량보다는 흐름 용량을 나타낸다.
  • 이동 방향: "어느 방향으로, 또는 양방향으로, 무엇인가 움직였는가?" 이것은 종종 화살표로[11] 보여진다.
  • 유속: "어떤 속도로 또는 얼마나 많은 시간 동안 무언가가 움직입니까?" 이것은 움직임의 양과 비슷하지만 구별되는 비율 변수다. 예를 들면 평균 차량 속도 또는 풍속을 이용하여 고속도로 교통 수준을 나타내는 것이다.

이것들은 별개의 유형의 지도가 아니다; 흐름 지도는 이러한 모든 측면을 동시에 나타낼 수 있다.

그동안 플로우 맵의 주제가 된 현상의 종류는 다양하다. 인간 지리와 관련된 주제로는 이주, 여행, 국제 무역, 물류, 공익 사업(수도, 하수, 전기, 통신), 교통 등이 있다. 다른 것들은 물리적 지리와 관련이 있다: 흐름, 바람, 야생동물 이주 등.

플로우 맵 유형

2014년 현재 모든 상용 여객 항공사 노선의 출발지-목적지 흐름도. 밝은 노란색은 높은 항공 경로 밀도를 나타낸다.

주제에서의 흐름 지도의 분산, 그리고 임호프의 흐름 측면의 상대적 중요성은 여러 가지 설계 전략으로 이어졌다. 1987년 논문에서 메리 팍스는 그녀의 리스트가 포괄적이지 않고 여기에 더 많은 것들이 포함되었음에도 불구하고 널리 인용되어 온 몇 가지 뚜렷한 유형의 흐름 지도를 확인했다.[12] 이 종류들은 원형이다; 실제 지도는 몇 가지 유형의 몇몇 측면을 결합할 수 있다.

원산지 지도

이 유형에서 주요 목적은 두 장소 간의 연결의 존재를 보여주는 것이며, 흐름 및/또는 방향의 표현을 동반하는 경우가 많다.[11] 경로는 일반적으로 관객에게 중요하지 않기 때문에 연결선이 직선적이거나 약간 구부러지는 경우가 많다. 이 양식의 일반적인 예는 항공사 노선도를 들 수 있다. 파크는 (단일 출발지 또는 목적지로부터) 네트워크 맵과 구별되지만, 이는 지리적 패턴의 차이점이며, 디자인은 두 유형 모두에서 매우 유사하다.

원산지 지도는 연결선의 도식적 형태에 독특한 설계 초점이 맞춰져 있다. 직선은 그리기 쉽지만, 특히 긴 선과 짧은 선이 서로 겹쳐져 서로와 목적지를 가릴 때 문제를 일으킬 수 있다. 그들은 또한 허황된 표정을 지을 수 있다. 이러한 이유로, 일반적으로 원형 호인 곡선은 미적으로 더 보기 좋게 선호된다. 그들은 또한 선과 점의 간섭을 피하기 위해 조정될 수 있는 능력을 가지고 있다.[13] 초기 자동화된 라인 생성 알고리즘은 일반적으로 직선이었지만,[8] 최근의 알고리즘은 곡선 생성에 성공했다.[14]

유통지도

찰스 조셉 미너드의 프랑스 와인 수출 지도는 유통 흐름도의 초기 사례인 1864년도의 프랑스 와인 수출도.

이러한 유형은 원점 목적지 노드, 그 노드들 사이의 이동 경로(일반적으로 매우 일반화됨), 흐름의 볼륨에 균형 잡힌 초점을 두고 예시된다. 미네르트로 거슬러 올라가는 가장 일반적인 예는, 일련의 노드 지역이나 항구 도시들, 그리고 공통의 바닷길을 따라 항해하는 것을 보여주는 지도다. 분포도에서 경로는 출발지로부터 몇 개의 목적지 총계에 비례하는 폭을 남겨두고, 각 목적지를 향해 "분산"하는 경로로 나뉜다.

유통 지도를 설계하려면 적절한 폭과 부드러운 곡선 각도로 나누도록 흐름 선 초안을 작성할 때 주의와 수완이 필요하다. 연산 실험은 이러한 것들을 자동으로 발생시킬 수 있는 가능성을 보여주었지만,[1] 오늘날에는 대부분 GIS와 그래픽 소프트웨어를 사용하여 반수동으로 그린다.[11]

네트워크 경로 맵

전형적인 개략적인 운송 지도는 네트워크 경로 맵의 단순한 형태로서, 고도로 일반화된 운송 경로에 초점을 맞추고 있다.

이러한 유형의 흐름 지도는 원래 아일랜드의 하니스 지도에서 유래한다.[3] 그것은 그것의 출발지/목적지 노드보다 네트워크의 경로에 더 초점을 맞춘다. 노선은 정밀하거나 고도로 일반화될 수 있으며(많은 통과 지도에서와 같이), 흐름의 양이나 속도를 나타낼 수도 있고 아닐 수도 있다. 일반적인 예가 고속도로 교통 지도다.

연속/질량 흐름도

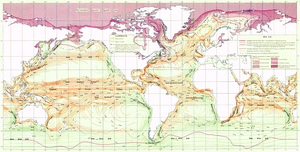
능률화 기법을 사용한 1943년 해류 지도. 색상을 사용하여 고온 및 한랭 전류를 구별하십시오.

모든 흐름이 선형 네트워크를 따라 발생하는 것은 아니다; 2차원 및 3차원 질량도 흐를 수 있는데, 특히 물(예: 해류)과 공기(바람)가 그렇다. 그들의 움직임은 벡터장으로 모델링될 수 있는데, 그 안에서 움직임의 크기와 방향을 공간의 어느 지점에서나 측정할 수 있다.[9]: 149 위의 임호프 목록에서는 이것을 시각화하는 지도, 흔히 질량 흐름도 또는 연속 흐름도라고 [15]하는 지도는 흐름의 방향과 속도에 초점을 맞추고 있는 반면, 출발지/목적지, 이동경로 등의 다른 측면은 대체로 의미가 없다.

1688년 에드먼드 핼리는 공기 흐름의 방향을 지향하는 일련의 단선 세그먼트를 사용하여 무역풍을 지도화했다.[4]: 69 20세기 초 기상 지도에서 이 기술은 풍속과 방향을 나타내는 복잡한 상징인 바람막이로 정교하게 표현되었다. 단위 벡터와 스트림렛은 점 기반 흐름 기호에 대한 일반 용어로 제안되었지만 둘 다 널리 사용되지 않는다.[16] 특히 래스터 GIS 데이터 또는 샘플 포인트 데이터(예: 기상 관측소)를 사용하여 컴퓨터 알고리즘에 의해 쉽게 생성될 수 있다.[17] 이 접근방식은 일반적인 흐름도보다는 비례점 기호와 더 유사하다.

벡터장을 위한 또 다른 시각화 옵션은 서로 유입될 수 있는 점들을 연결하는 유선형을 그리는 것이다; 이것은 19세기 초부터 해류를 나타내기 위해 일반적으로 사용되어 왔다.[4]: 82 토블러의 1981년 컴퓨터 알고리즘 중에는 "스트레클라인"을 생성하기 위한 벡터 필드의 모델이 있었고, 그 후의 작업은 성과가 향상되었다.[7][16]

중량 스케일링

흐름의 양이나 속도를 시각화하는 가장 일반적인 기법은 크기의 시각적 변수, 특히 선 두께(보통 점이나 밀리미터로 측정)를 통해서이다. 즉, 크기는 총량에서 훨씬 직관적이기 때문에 다른 시각적 변수(색깔 색 또는 색상 값 등)도 속도에 대해 고려될 수 있다. 선 두께를 결정하는 다음의 방법은 비례 기호 맵의 스케일링 방법과 매우 유사하다.[11]

가장 일반적인 방법은 선택된 기본 값 v에0 대해 임의로 선택한 가중치 w에0 기초하여 주어진 선 w의 가중치를 값 v에 직접 비례하여 계산하는 것이다(흔히 그렇지만 반드시 최소값은 아님).

이것은 독자들이 상대적 가중치에 기반한 상대적 가치 비율에 대한 직관적인 판단을 하는데 도움을 준다; 다른 선보다 두 배 더 두꺼운 선은 두 배의 가치를 나타낸다. 그러나 최고값과 최저값 사이에 매우 높은 수준의 변동이 있을 때(일반적으로 흐름망과 설계의 지형에 따라 달라지지만 25:1 이상), 결과적 지도가 문제가 될 수 있으며, 압도적으로 굵은 선과 거의 보이지 않는 얇은 선이 있을 수 있다. 비록 그런 능력을 직관적으로의 무게 비율을 판단하는 이 사건 다른 대안은(wmax과 wmin)고 그들 사이의 선형 보간법을 수행하는 최소 및 최대 중량을 설정하기:w− wm나의 아니 지금 그녀를 x− wm나의)'v'− vm나의 'v'지금 그녀를 x− vm나의{\displaystyle{\frac{w-w_{분}}.{w_{m

세 번째 대안은 단순히 서수 가중치(두께, 중간, 얇음 등)를 사용하여 분류된 서수 변수 또는 양적 변수(흔히 이 맥락에서 범위 등급이라고 함)를 나타내는 것이다. 이로 인해 독자는 가치 차이를 직관적으로 판단할 수 있는 능력도 상실되지만 전체적인 단순성의 장점이 있다.

이러한 모든 유형의 스케일링에서 범례는 일반적으로 비례 기호 맵의 범례와 유사한 방식으로 각 값과 함께 선 두께의 샘플 세트를 보여준다.

기타 유형의 흐름도

주요 기사: 흐름도
주요 기관 시스템에 전달된 심장 출력의 상대적 비율을 보여주는 비카토그래픽 흐름도

지도 기록의 흐름 맵 외에도 비지질 흐름을 시각화하는 몇 가지 다른 방법이 있다.

참고 항목

참조

  1. ^ a b Phan, Doantam; Xiao, Ling; Yeh, Ron; Hanrahan, Pat; Winograd, Terry (2005). "Flow Map Layout". Proceedings of the 2005 IEEE Symposium on Information Visualization (InfoVis '05): 219–224. doi:10.1109/INFVIS.2005.1532150. ISBN 0-7803-9464-X.
  2. ^ Robinson, Arthur H. (Dec 1955). "The 1837 Maps of Henry Drury Harness". The Geographical Journal. 121 (4): 440–450. doi:10.2307/1791753. JSTOR 1791753.
  3. ^ a b Griffith, Richard John; Harness, Henry Drury (1838). Atlas to Accompany 2nd Report of the Railway Commissioners. Ireland.
  4. ^ a b c Robinson, Arthur H. (1982). Early Thematic Mapping in the History of Cartography. University of Chicago Press. pp. 147–154.
  5. ^ Tufte, Edward (2006). Beautiful Evidence. Graphics Press.
  6. ^ Jacobs, Frank. "The Minard Map - "The best statistical graphic ever drawn"". Big Think. Retrieved 13 November 2020.
  7. ^ a b Tobler, Waldo R. (January 1981). "A Model of Geographic Movement". Geographical Analysis. 13 (1): 1–20. doi:10.1111/j.1538-4632.1981.tb00711.x.
  8. ^ a b Tobler, Waldo R. (1987). "Experiments in Migration Mapping by Computer". The American Cartographer. 14 (2): 155–163. doi:10.1559/152304087783875273.
  9. ^ a b Imhof, Eduard (1972). Thematische Kartographie. Berlin: De Gruyter.
  10. ^ 로빈슨, 아서 H, 카토그래피 원소, 제2판, 뉴욕: 와일리, 1960.
  11. ^ a b c d Dent, Borden D.; Torguson, Jeffrey S.; Hodler, Thomas W. (2009). Cartography: Thematic Map Design (6th ed.). McGraw-Hill. pp. 188–201.
  12. ^ Parks, Mary J. (1987). American flow mapping: A survey of the flow maps found in twentieth century geography textbooks, including a classification of the various flow map designs. Georgia State University: Unpublished M.A. thesis.
  13. ^ Jenny, Bernhard; Stephen, Daniel M.; Muehlenhaus, Ian; Marston, Brook E.; Sharma, Ritesh; Zhang, Eugene; Jenny, Helen (2018). "Design principles for origin-destination flow maps". Cartography and Geographic Information Science. 45 (1): 62–75. doi:10.1080/15230406.2016.1262280.
  14. ^ Jenny, Bernhard; Stephen, Daniel M.; Muehlenhaus, Ian; Marston, Brooke E.; Sharma, Ritesh; Zhang, Eugene; Jenny, Helen (2017). "Force-directed layout of origin-destination flow maps". International Journal of Geographical Information Science. 31 (8): 1521–1540. doi:10.1080/13658816.2017.1307378.
  15. ^ T. Slocum, R. McMaster, F. Kessler, H. Howard(2009). 주제 지도학 및 지리학, 제3의 Edn, 252페이지. Pearson 프렌티스 홀: Upper Saddle River, NJ, 페이지.360-369.
  16. ^ a b Turk, G.; Banks, D. (August 1996). "Image-guided streamline placement". SIGGRAPH '96: Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques: 453–460. doi:10.1145/237170.237285. ISBN 0897917464.
  17. ^ Lavin, S.J.; Cerveny, R.S. (1987). "Unit-vector density mapping". The Cartographic Journal. 24 (2): 131–141. doi:10.1179/caj.1987.24.2.131.


외부 링크