자석 사이의 힘

자석은 전자석의 법칙으로 인해 서로에게 힘과 토크를 발휘한다.자석의 끌어당김 영역의 힘은 핵 궤도를 선회하는 전자의 미세한 전류와 물질을 구성하는 기본 입자(전자 등)의 내적인 자력에 기인한다.이 두 가지 모두 자기장을 생성하며 외부 자기장의 영향을 받는 자기 쌍극이라고 불리는 아주 작은 전류의 루프처럼 잘 모델링되어 있다.자석 사이의 가장 기본적인 힘은 자석 쌍극자-디폴자 상호작용이다.만약 두 개의 자석을 구성하는 자석 쌍극자석이 모두 알려져 있다면, 첫 번째 자석의 쌍극자와 두 번째 자석의 쌍극자 사이의 모든 상호작용을 합산하여 두 자석의 순력을 결정할 수 있다.

두 자석 사이의 힘을 자기 전하가 자석 위에 퍼져 있는 자석 사이의 힘 때문에 두 자석 사이의 힘을 모형화하는 것이 종종 더 편리하다.양극과 음극 자기 전하가 항상 자화된 물질의 끈에 의해 연결된다. 분리된 자기 전하가 존재하지 않는다.이 모델은 자기 전하가 분배되는 방법에 대한 좋은 모델이 있는 단순 자석 사이의 힘을 예측하는 데 효과적이다.

자기극 vs 원자전류

자석의 장은 원자 수준의 작은 자석 쌍극으로 구성된 모든 자화된 체적 원소의 장의 합이다.이 모든 쌍극자장의 직접적인 합계는 단지 하나의 자석의 장을 얻기 위해 3차원 통합이 필요할 것이며, 이것은 복잡할 수 있다.

동질 자기화의 경우 스톡스의 정리를 이용하여 적어도 두 가지 다른 방법으로 문제를 단순화할 수 있다.자석화 방향을 따라 통합하면 자석의 끝 표면을 제외하고 통합선을 따라 있는 모든 쌍극이 서로를 취소한다.그러면 장(場)은 자석의 끝 면에 퍼져 있는 (수학적) 자기 전하를 통해서만 나타난다.반대로 자석화 방향에 직교하는 자석화 영역 위에 통합할 때, 이 영역 내의 쌍극점은 자석의 외부 표면을 제외하고 서로를 취소한다. 단, 이 영역 내의 쌍극은 (수분적으로) 링 전류에 합친다.이것을 앰페르 모델이라고 한다.두 모델 모두 자석 표면에 걸친 2차원 분포만 고려해야 하는데, 이는 원래 3차원 문제보다 간단하다.

자기 충전 모델:자기장전하 모델에서 영구 자석의 극 표면은 자기장 선의 근원인 소위 자기장전하, 북극의 북극 입자, 남극의 남극 입자로 덮인다고 상상한다.자기 전하에 의한 장은 전기 전하가 아닌 자석으로 쿨롱의 법칙을 통해 얻는다.자기장 분포가 알려진 경우, 극 모델은 자기장 강도 H의 정확한 분포를 자석 내부와 외부에 제공한다.표면 전하 분포는 자석이 균일하게 자화되고 평평한 끝 면(원통이나 프리즘 등)을 가진 경우 균일하다.

암페어 모델:암페어 모델에서 모든 자기화는 물질 전체에 걸쳐 암페리아 전류라고도 불리는 미세한, 또는 원자적인 원형의 결합 전류의 영향 때문이다.이러한 미세한 결합 전류의 순효과는 자석이 자석의 루프 안에서 루프를 타고 흐르는 거시적인 전류가 있는 것처럼 작용하게 하고 자기장은 루프에 정상으로 작용하게 하는 것이다.그런 흐름으로 인한 밭은 그 후 바이오트-사바트 법칙을 통해 얻는다.암페어 모델은 자석의 내부와 외부에 모두 정확한 자속 밀도 B를 제공한다.자석의 표면에서 암페리아 전류를 계산하는 것은 때때로 어렵다.

자기 쌍극자 모멘트

자석에서 멀리 떨어져 있는 그것의 자기장은 그것의 총 자기 쌍극자 모멘트로 특징지어지는 쌍극자장에 의해 거의 항상 (좋은 근사치로) 설명된다.자석 모멘트가 0이 아닌 한 자석의 형태에 상관없이 이것은 사실이다.쌍극장의 한 가지 특징은 자기장의 강도가 자석의 중심에서 거리의 입방체와 반비례하여 떨어진다는 것이다.

그러므로 자석의 자기 모멘트는 강도와 방향을 측정하는 척도다.전류의 순환, 막대 자석, 전자, 분자, 그리고 행성은 모두 자기 모멘트를 가지고 있다.더 정확히 말하면, 자기 모멘트라는 용어는 일반적으로 시스템의 자기 쌍극자 모멘트를 가리키는데, 이것은 일반 자기장의 다중극자 팽창에서^{[note 1]} 첫 번째 용어를 생산한다.

외부 자기장에 의해 자석에 가해지는 토크와 힘은 모두 자석의 자기 모멘트에 비례한다.자기 모멘트는 벡터다: 그것은 크기와 방향을 모두 가지고 있다.자석의 방향은 자석의 남극에서 북극(자석 내부)까지 가리킨다.예를 들어 나침반 안에 있는 것과 같은 막대 자석의 자기 모멘트 방향은 북극이 가리키는 방향이다.

물리적으로 정확한 앰페르 모델에서 자기 이중극 모멘트는 극소량의 전류 루프에 기인한다.충분히 작은 전류 루프, I 및 영역 A의 경우 자기 쌍극자 모멘트는 다음과 같다.

여기서 m의 방향은 전류와 우측 규칙을 사용하여 결정된 방향의 영역에 대해 정상이다.이와 같이 자기 쌍극자 모멘트의 SI 단위는 암페어 미터다².더 정확히 말하면, 회전이 많은 솔레노이드를 설명하기 위해 자기 쌍극자 모멘트의 단위는 암페어 회전 미터다².

자기 충전 모델에서, 자기 쌍극자 모멘트는 거리 d로 분리된 두 개의 동일하고 반대되는 자기 전하에 기인한다.이 모델에서 m은 전하에 의한 전기 쌍극자 모멘트 p와 유사하다.

여기서 q는_m '충전 요금'이다.자석 쌍극 모멘트의 방향은 음극 남극에서 이 작은 자석의 양극으로 가리킨다.

불균일 자기장으로 인한 자기력

자석은 자기장 구배를 따라 그려진다.이것의 가장 간단한 예는 두 자석의 반대편 극의 끌어당김이다.모든 자석은 극점 근처에서 더 강한 자기장을 생성한다.만약 두 개의 분리된 자석의 반대편 극이 서로 마주보고 있다면, 각각의 자석은 다른 자석의 극 근처의 더 강한 자기장으로 빨려들어간다.그러나 만약 극이 서로 마주보고 있다면, 그들은 더 큰 자기장에서 물러난다.

자기충전 모델은 이 힘에 대한 정확한 수학적 형태를 예측하고 질적으로 이해하기 쉽다.만약 자석이 균일한 자기장에 놓여진다면, 두 극은 서로 반대되는 자기 전하를 가지고 있기 때문에 동일한 자기력을 느낄 것이다.그러나 다른 자석으로 인해 자석이 균일하지 않은 장에 놓이면 큰 자장을 경험하는 극이 큰 힘을 경험하게 되고 자석에 그물 힘이 생기게 된다.만약 자석이 자기장과 일직선이 되어, 극점 근처에서 같은 방향으로 향하게 되는 두 개의 자석에 대응한다면, 그것은 더 큰 자기장으로 빨려 들어갈 것이다.만약 두 개의 자석이 서로 마주보고 있는 것과 같이 반대로 정렬되어 있다면, 자석은 더 높은 자기장의 영역에서 밀어낼 것이다.

앰페르 모델에서는 균일하지 않은 자기장으로 인해 자기 이중극에 작용하는 힘도 있지만, 이는 자기 이중극을 구성하는 현재 루프에 작용하는 로렌츠 힘 때문이다.전류 루프 모델의 경우 얻어진 힘은

여기서 gradient∇은 단위 거리당 m · B의 수량의 변화이며, 방향은 m · B의 최대 증가량이다.이 방정식을 이해하려면 도트 productm · B = mB cos(cos)에 유의하십시오. 여기서 m과 B는 m과 B 벡터의 크기를 나타내고 θ은 이들 사이의 각도임을 알 수 있다.m이 B와 같은 방향일 경우 도트 제품은 양성이며, 그라데이션 포인트는 자석을 B-필드(더 엄격하게 더 큰 m · B)의 영역으로 끌어당기는 '업힐(uphill)은 자석을 B-필드(m · B)가 더 높은 영역으로 끌어당긴다.B는 자기장의 강도와 방향을 나타낸다.이 방정식은 0 크기의 자석에만 엄격히 유효하지만, 너무 큰 자석은 아닌 경우 좋은 근사치가 되는 경우가 많다.더 큰 자석에 대한 자력은 자석들을 그들 자신의 m을 가진 더 작은 영역으로 나눈 다음 이들 각각의 영역에 대한 힘을 합쳐서 결정된다.

자기 충전 모델

자석 충전 모델은 자석 사이의 자력이 극 부근의 자기 전하에 기인한다고 가정한다.이 모델은 자기장이 복잡해질 때 자석에 가깝게 작용하기도 하고, 자석의 세밀한 모양과 자성에만 의존하는 것이 자석 쌍극자 기여에 그치지 않는다.공식적으로 필드는 다중 홀 확장으로 표현될 수 있다.암페어 모델에서는 쌍극장, 쿼드폴장, 문어장 등이 더해져 있지만 수학적으로는 매우 번거로울 수 있다.

자기력 계산

두 자석 사이의 매력적이거나 반발력을 계산하는 것은 일반적으로 자석의 모양, 자화, 방향, 분리에 따라 달라지기 때문에 매우 복잡한 연산이다.자기충전 모델은 '자기충전'이 어떻게 자기 극에 분산되는지에 대한 일부 지식에 의존한다.그것은 그때까지도 간단한 구성에만 정말로 유용하다.다행히도, 이 제한은 많은 유용한 사례들을 포함한다.

두 자성극 사이의 힘

만약 두 극이 단일 점으로 표현될 만큼 충분히 작다면, 그것들은 점 자기 전하로 간주될 수 있다.고전적으로 두 자극 사이의 힘은 다음과 같이 주어진다.^[1]

어디에

• F는 힘(SI 단위: 뉴턴)
• q와_m1 q는_m2 자기 폴에 대한 자기 전하의 크기(SI 단위: 암페어 미터)
• μ는 간섭 매체의 투과성(SI 단위: 암페어당 테슬라 미터, 미터당 헨리 또는 암페어 제곱당 뉴턴)
• r은 분리(SI 단위: 미터)이다.

극의 묘사는 실제의 자석을 설계하는 자석들의 연습에 유용하지만, 실제 자석은 하나의 남북보다 더 복잡한 극의 분포를 가지고 있다.그러므로 극구 사상의 구현은 간단하지 않다.어떤 경우에는 아래에 제시된 보다 복잡한 공식 중 하나가 더 유용할 것이다.

영역 A의 두 근처 자화 표면 사이의 힘

가까운 두 자화면 사이의 기계적 힘은 다음과 같은 방정식으로 계산할 수 있다.이 방정식은 프링 효과가 미미하고 공극 부피가 자화된 물질의 부피보다 훨씬 작은 경우에만 유효하며, 각 자화 표면의 힘은 다음과 같다.^[2][3][4]

여기서:

• A는 각 표면의 면적(m²)이다.
• H는 A/m에 있는 그들의 자기장이다.
• μ는₀ 공간의 투과성으로, 4××10⁻⁷ T·m/A와 같다.
• B는 플럭스 밀도(T)이다.

이 방정식의 도출은 근처의 두 전기 충전 표면 사이의 힘과 유사하며,^[5] 이는 판 사이의 장이 균일하다고 가정한다.

두 막대 자석 사이의 힘

${\displaystyle 두}$ 개의 동일한 원통형 막대 자석 사이에 큰 거리 $x{\displaystyle }$ ${\displaystyle \gg }$ R ${\displaystyle x\gg R}$에 있는 힘은 대략 다음과 같다$$.^[2]

어디에

• B는₀ 각 극에 매우 가까운 플럭스 밀도(T)이다.
• A는 각 극의 면적(m²)이다.
• L은 각 자석의 길이(m)이다.
• R은 각 자석의 반지름(m)이며,
• x는 두 자석 사이의 분리(m)이다.

극의 플럭스 밀도와 자석의 자성을 연관시킨다.

이러한 공식은 끝 면에 걸쳐 균일한 분포가 아닌 점 같은 자기 전하 분포를 가정하며, 이는 비교적 먼 거리에서만 좋은 근사치라는 점에 유의한다.중간 거리의 경우 숫자 방법을 사용해야 한다.

두 원통형 자석 사이의 힘

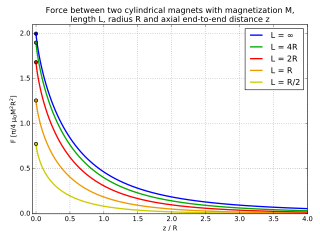
반지름 $R{\displaystyle }$ ${\displaystyle R}$과(와$)$ 자석 이중극이 정렬된 $길이{\displaystyle }$ L ${\displaystyle L$이 있는 두 개의 원통형 자석에 대해서는 타원형 통합을 사용하여 힘을 분석적으로 계산할 수 있다.^[6]한계 $x{\displaystyle }$ ${\displaystyle \gg }$ ${\displaystyle R}$ ${\displaystyle x\gg R}$에서 힘은 다음과 같이 근사할 수 있다$.$^[7]

여기서 $M{\displaystyle }$ ${\displaystyle M}$은 자석의 자화, $x{\displaystyle }$ ${\displaystyle x}$은 자석 사이의 거리.$x{\displaystyle }$ ${\displaystyle x$의 작은 값의 경우 0에 가까운 거리에 대한 힘이 커짐에 따라 결과가 잘못되었다.

자석이 긴 경우(${\displaystyle }$ ${\displaystyle \gg }$ ${\displaystyle R}$ ${\displaystyle L\gg$ R$}),$ 자석 ${\displaystyle {B\mathrm{}}_{}}$ $0{\displaystyle {}_{}}$ ${\$에 매우 가까운 자속 밀도의 측정은 $다음{\displaystyle }$ 공식에 의해$$ M ${\displaystyle M}$과 대략 관련이 있다$$.

유효 자기 쌍극자 모멘트는 다음과 같이 기록할 수 있다.

여기서 $V{\displaystyle }$ ${\displaystyle V}$은(는) 자석의 볼륨이다.실린더의 경우 이 $값$은 V${\displaystyle }$= ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ 2 L ${\displaystyle$V=\$pi R^{$2}$L$이고,$$M {\$displaystyle$ M$}$은 쌍극자의 자기화 필드임.

$L{\displaystyle }$ ${\displaystyle \ll }$ ${\displaystyle x}$ ${\displaystyle L\ll x}$ 포인트$$ 쌍극점 근사치를 구하면,

두 자석 쌍극자 사이의 힘의 표현과 일치한다.

암페어 모델

프랑스의 과학자 안드레 마리 암페르는 영구 자석에 의해 생성되는 자력과 전자석들에 의해 생성되는 자력이 같은 종류의 자기라는 것을 발견했다.

그 때문에 영구 자석의 강도는 전자석의 강도와 같은 용어로 표현할 수 있다.

전류가 흐르는 전선의 평평한 루프인 전자석의 자력 강도는 루프 크기에 비해 큰 거리에서 측정된 전류가 흐르는 전선에 비례하며, 이 루프의 표면적에 비례한다.

영구 자석의 강도를 전자석과 같은 용어로 표현하기 위해 영구 자석은 부피 전체에 작은 전류 루프를 포함하는 것처럼 생각되며, 그 다음 자석의 자력은 각 루프(암페어)의 전류에 비례하고 ea의 표면에 비례하는 것으로 확인된다.ch 루프(제곱미터 단위), 재료 내 전류 루프의 밀도(제곱미터당 단위)에 비례하므로 영구 자석의 자기 강도의 치수는 제곱미터당 암페어 곱제곱미터로 미터당 암페어이다.

그렇기 때문에 이러한 작은 전류 루프는 실제로 영구 자석에 존재하지 않더라도 미터당 암페어가 정확한 자력 단위인 것이다.

암페어 모델의 유효성은 자성물질을 마치 전류루프(current-loups)로 구성된 것처럼 생각하는 것이 허용된다는 것을 의미하며, 총효과는 각 전류루프(current-loop)의 효과의 합이므로, 실제 자석의 자성효과는 거리에 있는 작은 자성물질의 자력효과 합으로 계산할 수 있다.각 조각의 크기에 비해 훌륭하다.

이것은 실제 자석의 자기장 계산에 매우 유용하다; 그것은 많은 양의 작은 힘을 포함하며, 손으로 하지 말고, 당신의 컴퓨터가 그렇게 하도록 하라; 컴퓨터 프로그램이 알아야 할 모든 것은 서로 매우 멀리 떨어져 있는 작은 자석 사이의 힘이다.

그러한 계산에서, 종종 각각의 (같은 크기의) 작은 자석 물질들이 똑같이 강한 자력을 가지고 있다고 가정하지만, 이것은 항상 사실이 아니다: 다른 자석 근처에 있는 자석은 다른 자석의 자성을 바꿀 수 있다.영구 자석의 경우 이것은 보통 작은 변화일 뿐이지만, 철심 주위에 감긴 와이어로 구성된 전자석이 있고, 그 코어 근처에 영구 자석을 가져온다면, 그 코어의 자기화는 급격하게 변할 수 있다(예를 들어, 와이어에 전류가 없으면 전자석은 자석이 아니라 w).영구 자석이 가까이 오면 전자석의 중심은 자석이 된다).

따라서 암페어 모델은 영구 자석의 자기장 계산에 적합하지만 전자석의 경우 자기 회로 접근법을 사용하는 것이 더 나을 수 있다.

자기 쌍극-디폴 상호작용

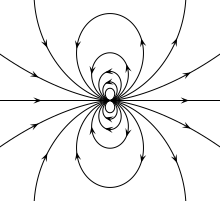
두 개 이상의 자석이 모양과 크기가 중요하지 않을 정도로 작거나 충분히 먼 경우, 두 자석은 모두₂ 자기 모멘트를 가진₁ 자석 쌍극으로 모델링할 수 있다.균일하게 자화된 구형 자석의 경우, 이러한 자석의 외부 장은 정확히 쌍극자장이기 때문에 이 모델은 유한한 크기와 거리에서도 정밀하다.^[8]

벡터 표기법에서 자기 쌍극자의 자기장은 다음과 같다.

어디에

• B는 밭이다.
• r은 쌍극자 위치에서 필드가 측정되는 위치까지의 벡터다.
• r은 r의 절대값: 쌍극자로부터의 거리
• ${\displaystyle \stackrel{}{\mathbf{r}}}$ ${\displaystyle \stackrel{}{}}$= ${\displaystyle r}$ ${\displaystyle$ {\hat {\$mathbf {r}}}}}}}}은(는$$)$ r에 평행한 단위 벡터;
• m은 쌍극자 모멘트다.
• μ는₀ 자유 공간의 투과성이다.
• Δ는³ 3차원 델타 함수다.^{[note 2]}

이것은 정확히 점 쌍극자의 필드, 정확히 임의 필드의 다중극 확장에서의 쌍극자 용어, 그리고 대략 먼 거리의 쌍극자 같은 구성의 필드다.

좌표계가 m의₁ 중심에 위치하도록 이동하고 z축이₁ m의 방향을 가리키도록 회전하는 경우 이전 방정식은 다음과^[9] 같이 단순화된다.

여기서 변수 r과 θ은 m의₁ 원점을 가진 기준 프레임에서 측정되며 m이₁ z 방향을 가리키는 원점에 있도록 방향을 정한다.이 프레임을 Local 좌표라고 하며 오른쪽 그림에서 볼 수 있다.

한 자석 쌍극자가 다른 자석 쌍극자에 가해지는 힘은 위에서 주어진 첫 번째 쌍극자의 자기장을 사용하고 위에서 주어진 힘 방정식을 이용하여 두 번째 쌍극자의 자기장으로 인한 힘을 결정함으로써 결정된다.벡터 표기법을 사용하여 자기 쌍극자 m에₂ 대한 자기 쌍극자 m의₁ 힘은 다음과 같다.

여기서 r은 쌍극자 모멘트 m에서₁ 쌍극자 모멘트 m까지의₂ 거리-벡터로서, r = r. m에₁ 작용하는 힘은 반대 방향에 있다.예를 들어 z 방향을 가리키고 z 축에 정렬되고 거리 z로 구분되는 두 자석에 대한 자기력은 다음과 같다.

${\displaystyle \mathbf{F}(z,}$ m ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}}$m ${\displaystyle {2\mathrm{}}_{}}$)${\displaystyle }$=${\displaystyle }$- ${\displaystyle 3\frac{\mathrm{}}{}}$ ${\displaystyle \frac{{}_{}{}_{}}{}}$ ${\displaystyle \frac{{0\mathrm{}}_{}}{}}$ 1 m 1 ${\displaystyle \frac{{}_{}{}_{}}{}}$ 2 ${\displaystyle \frac{{}_{}}{\mathrm{}}}$ ${\displaystyle \frac{\pi }{}}$ ${\displaystyle \frac{{z\mathrm{}}^{}}{}}$ ${\displaystyle \frac{{}^{}}{}}$ ${\$ z$^4$ z-방향

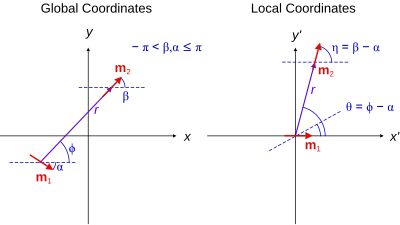
최종 공식은 다음에 표시된다.그것들은 전지구 좌표계로 표현된다.

메모들

참조

참고 항목

• 마그네틱 모터