사극

4극 또는 4극은 이상적인 형태로 존재할 수 있는 전하나 전류, 중력 질량의 배열 중 하나이지만, 그것은 보통 다양한 복잡성의 순서를 반영하는 더 복잡한 구조의 다극 확장의 일부일 뿐이다.

수학적 정의

4극 모멘트 텐서 Q는 2등급 텐서이다. 3×3 행렬이다.몇 가지 정의가 있지만 일반적으로 트레이스리스 형식으로 기술됩니다( $Q_{xx}+Q_{yy}+Q_{zz}=0$ : Q $Q_{xx}+Q_{yy}+Q_{zz}=0$ + $Q_{xx}+Q_{yy}+Q_{zz}=0$ y $Q_{xx}+Q_{yy}+Q_{zz}=0$ + $Q_{xx}+Q_{yy}+Q_{zz}=0$ $Q_{xx}+Q_{yy}+Q_{zz}=0$ $Q_{xx}+Q_{yy}+Q_{zz}=0$ { $displaystyle Q_{x}+).$ $Q_{y}+Q_{zz}=0}).$ 4극 모멘트 텐서는 따라서 9개의 성분이 있지만, 전위 대칭과 제로 트레이스 특성 때문에 이 형태에서는 5개 요소만 독립적입니다.

중력 4극의 경우 점 전하 또는 질량의 이산 시스템의 경우, 각각 $q_{\ell }$ $q_{\ell }$ ${\$ {\ $displaystyle q_{\ell$ 또는 $m_{\ell }$ $m_{\ell }$ ${\$ {\ $displaystyle m_$ ${\ell$ $m_{\ell }$ ${\vec {r}}_{\ell }=\left(r_{x\ell },r_{y\ell },r_{z\ell }\right)$ r $=$ ( ${\vec {r}}_{\ell }=\left(r_{x\ell },r_{y\ell },r_{z\ell }\right)$ ${\vec {r}}_{\ell }=\left(r_{x\ell },r_{y\ell },r_{z\ell }\right)$ , , ${\vec {r}}_{\ell }=\left(r_{x\ell },r_{y\ell },r_{z\ell }\right)$ y ${\vec {r}}_{\ell }=\left(r_{x\ell },r_{y\ell },r_{z\ell }\right)$ , ${\vec {r}}_{\ell }=\left(r_{x\ell },r_{y\ell },r_{z\ell }\right)$ z $ℓ$ ) ${\vec {r}}_{\ell }=\left(r_{x\ell },r_{y\ell },r_{z\ell }\right)$ { $styleft$ } { style {\ $styleft }$ $ll }\right)}$ 좌표계 ${\vec {r}}_{\ell }=\left(r_{x\ell },r_{y\ell },r_{z\ell }\right)$ 원점에 대해 Q 행렬의 구성요소는 다음과 같이 정의됩니다.

\displaystyle Q_{ij}=\sum _{\ell}q_{\ell}\left(3r_{i\ell}r_{j\ell}-\left\{vec {r}_{\ell}\right\^{2}\sum _{ij}\light}\left.}

x $,$ $y, z$ ( $displaystyle$ x $,y,z)$ 및 $x,y,z$ $\delta _{ij}$ $($ _ ${ij})$ 의 $\delta _{ij}$ 데카르트 $좌표$ 위에 있는 인덱스 $i$ , $(displaystyle$ i $,j)$ 는 $i,j$ 크로네커 델타입니다. $즉$ , x $,$ $y,$ $(표시 스타일$ x $,y,z)$ 가 $x,y,z$ 점으로부터 서로 $수직$ 인 n $($ 표시 $n$ $스타일$ n)까지의 거리에 대해 부호까지 같아야 합니다.

비추적 형태에서 4극 모멘트는 다음과 같이 표현된다.

Q_{ij}=\sum _{\ell}q_{\ell}r_{i\ell}r_{j\ell}

이 형식을 통해 빠른 다중극 방법에 관한 문헌에서 몇 가지 용도를 확인할 수 있습니다.이러한 두 형태 간의 변환은 유해한 ^[1]연산자를 사용하여 쉽게 이루어질 수 있습니다.

전하 밀도 또는 질량 밀도를 갖는 연속 시스템의 경우 $\rho (x,y,z)$ , y $\rho (x,y,z)$ ) { $displaystyle \rho (x,y,z$ Q의 구성요소는 데카르트 공간 ^[2]r 위의 적분에 의해 정의됩니다.

\displaystyle Q_{ij}=\int,\rho(\mathbf {r})\left(3r_i}r_{j}-\left\{vec {r}\right\^{2}\fright),d^{3}\mathbf {r}

다른 다극 모멘트와 마찬가지로, 이 경우 단극 또는 쌍극자 모멘트가 0이 아닌 경우, 4극 모멘트의 값은 좌표 원점의 선택에 따라 달라집니다.예를 들어 모노폴 모멘트가 없는 2개의 반대 부호 동일 강도점 전하의 다이폴은 원점이 두 전하 사이의 구성 중심에서 정확히 어긋나면 0이 아닌 4극 모멘트를 가질 수 있고, 원점을 중심으로 4극 모멘트를 0으로 낮출 수 있다.반대로 단극과 쌍극 모멘트는 사라지지만 4극 모멘트는 사라지지 않는 경우(예를 들어 사각형에 배치된 4개의 동일한 강도 전하), 4극 모멘트는 좌표에 의존하지 않는다.

각 전하가 전기장이나 중력장과 같은 " $1/r$ $1/r$ \ $displaystyle$ 1/ $r$ 전위의 소스인 경우, 4극 모멘트에서 전위의 기여는 다음과 같습니다.

\displaystyle V_{\text{q}(\mathbf {R})=sum frac {k}{i,j}{\frac {1}{2}Q_{\hat {R}{j},{\hat {R}}{j},

여기서 R은 전하계에서 원점을 갖는 벡터이고 Rθ는 R 방향의 단위 벡터이다. $즉$ , i $i=x,y,z$ $i=x,y,z$ $i=x,y,z$ (\ $displaystyle$ i $=x, y,$ z)의 $i=x,y,z$ R ${\hat {R}}_{i}$ ^ ${\hat {R}}_{i}$ ${\displaystyle$ { $R}_{i}}$ 는 ${\hat {R}}_{i}$ 원점에서 필드 지점을 가리키는 단위 벡터의 데카르트 성분입니다.여기서 k $(\displaystyle$ k $)$ 는 $k$ 필드의 유형과 사용되는 단위에 따라 달라지는 상수입니다.

전기 사중극

전기 4극장의 등전위 표면 등고선도

전기 4중극의 가장 간단한 예는 정사각형의 모서리에 배치된 양전하와 음전하를 번갈아 배치하는 것이다.이 배열의 모노폴 모멘트(전체 전하)는 0입니다.마찬가지로 쌍극자 모멘트는 선택된 좌표 원점에 관계없이 0입니다.그러나 좌표 원점을 어디에 배치하든 다이어그램에서 배열의 4극 모멘트를 0으로 줄일 수 없습니다.전하 4극의 전위는 다음과 같이 주어진다^[3].

{\displaystyle V_{\text{q}(\mathbf {R})=blac {1}{4\pi \varepsilon _{0}}{\frac {R}^{3}}\sum _{i,j}{\frac {1}{1}{{\frac {1}{1}{{{{1}{{{{{{{2}}}{ij}{ij}{i}}}{i}{i}}{i}{i}{i}}}{i}}{i}{i}}}}{{{

$\varepsilon _{0}$ 서 0 $(\$ 은 $\varepsilon _{0}$ $Q_{ij}$ 유전율이고 $Q_{ij}$ j(\ $displaystyle Q_{ij})$ 는 $Q_{ij}$ 위의 정의에 따릅니다.

다른^[4] 선원은 $Q_{ij}$ ({ $displaystyle Q_{$ }) 텐서 자체의 1/2 계수를 포함하며, 다음과 같다.

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

j

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

(

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

) (

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

-

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

2

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

r

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

2

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

i

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

)

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|{\vec {r}}\right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r}

( \

displaystyle Q

_ {

ij

} = \

int

, \

rho

( \

mathbf { r

} \

left

\

frac

{

3

} { } { } r

_ r

_ r _ r _ {

j

} \

frac

}

V_{\text{q}(\mathbf {R})=blac {1}{\pi \varepsilon _{0}}{\frac {1}{\mathbf {R}^{3}}\sum _{i,j}Q_{ij},{\hat {R}}}{\hat}{{{\}}}

이는 다중극 확장에 의해 발생하는 Legendre 다항식, 즉 $P_{2}(x)={\frac {3}{2}}x^{2}-{\frac {1}{2}}.$ 서 $P_{2}(x)={\frac {3}{2}}x^{2}-{\frac {1}{2}}.$ ) $P_{2}(x)={\frac {3}{2}}x^{2}-{\frac {1}{2}}.$ $P_{2}(x)={\frac {3}{2}}x^{2}-{\frac {1}{2}}.$ 2 $P_{2}(x)={\frac {3}{2}}x^{2}-{\frac {1}{2}}.$ $P_{2}(x)={\frac {3}{2}}x^{2}-{\frac {1}{2}}.$ - $P_{2}(x)={\frac {3}{2}}x^{2}-{\frac {1}{2}}.$ 2 $P_{2}(x)={\frac {3}{2}}x^{2}-{\frac {1}{2}}.$ . { $displaystyle P_{$ 2}(x) = $specfrac {3}{2}-{\frac {1}{$ }에 대한 연결을 보다 명확하게 한다. $}$

일반화: 멀티폴이 높음

극단적 일반화("점 옥토폴")는 다음과 같습니다. 예를 들어 모서리 길이가 a인 입방체의 8개 모서리에 있는 8개의 교대 점 전하입니다.이 배열의 "옥토폴 모멘트"는 "옥토폴 한계"에서 a $\lim _{a\to 0}{a^{3}\cdot Q}\to {\text{const. }}$ $\lim _{a\to 0}{a^{3}\cdot Q}\to {\text{const. }}$ $\lim _{a\to 0}{a^{3}\cdot Q}\to {\text{const. }}$ 3 $\lim _{a\to 0}{a^{3}\cdot Q}\to {\text{const. }}$ Q $\lim _{a\to 0}{a^{3}\cdot Q}\to {\text{const. }}$ 에 해당한다. ${\displaystyle_{a\to0}{a^{3}\cdotQ}에서 {\text{const.$ $\lim _{a\to 0}{a^{3}\cdot Q}\to {\text{const. }}$ 0이 아닌 $\lim _{a\to 0}{a^{3}\cdot Q}\to {\text{const. }}$ 3차 대각 텐서까지 $\lim _{a\to 0}{a^{3}\cdot Q}\to {\text{const. }}$ }}.더 높은^l 다중극(예: 2차)은 낮은 차수의 포인트 단극이 아닌 포인트 쌍극(예: 2차^l−1 단극, 8극, ...)의 쌍극자(사중극, 8극 등) 배열로 얻을 수 있다.

자기 사극

사극장을 생성하는 코일

도식 4극 자석('4극'

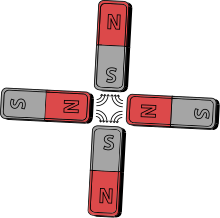
알려진 모든 자기 소스는 쌍극자장을 제공합니다.단, 동일한 막대 자석 4개를 서로 직각으로 배치하여 하나의 북극이 다른 극의 남쪽에 위치하도록 함으로써 자성 4극으로 할 수 있다.이러한 구성은 쌍극자 모멘트를 취소하고 4극자 모멘트를 제공하며, 그 장은 쌍극자 모멘트에 비해 먼 거리에서 더 빨리 감소합니다.

오른쪽에는 영구 자석이 포함된 자석 4극의 예가 나와 있습니다.유사한 개념 설계의 전자석(사극 자석이라고 함)은 일반적으로 입자 가속기와 빔 전송 라인에 하전된 입자의 빔을 집중시키는 데 사용됩니다. 이 방법은 강한 포커싱으로 알려져 있습니다.4개의 강철 극 팁이 있으며, 두 개의 반대되는 자기 북극과 두 개의 반대되는 자기 남극이 있습니다.강철은 극에 감긴 튜브의 코일에 흐르는 큰 전류에 의해 자화됩니다.또, 4극-다이폴 교차는, 비쌍핵자의 스핀에 그 부모 원자를 곱하는 것으로 얻을 수 있다.

변화하는 자기 4극 모멘트는 전자 복사를 발생시킨다.

중력 사극

질량 4극은 전하 밀도가 질량 밀도로 대체되고 질량이 항상 양이고 힘이 끌리기 때문에 음의 부호가 추가되는 전하 4극과 유사합니다.중력 전위는 다음과 같이 표현된다.

\displaystyle V_{\text{q}(\mathbf {R})=-{\frac {G}{2 \mathbf {R}^{3}}\sum _{i,j}Q_{i},{\hat {R}{j}.

예를 들어, 지구는 자전하고 있기 때문에 타원형이다.이것은 0이 아닌 4극 모멘트를 줍니다.지구에 가까운 인공위성에 있어서 이 4극에서 지구 중력장에 대한 기여는 매우 중요하지만, 1 ${\frac {1}{|\mathbf {R} |^{3}}}$ 3 $(\$ ${\frac {1}{|\mathbf {R} |^{3}}}$ 은 $\frac{1}{|\mathbf{R}|^3}$ 빠르게 떨어지기 때문에 달에게는 덜 중요하다.

질량의 4극 모멘트는 또한 일반 상대성 이론에서 중요하다. 왜냐하면, 시간이 바뀌면, 전기 또는 자기 쌍극자 및 더 높은 다중극에 의해 발생하는 전자기 방사선과 유사한 중력 방사선을 발생시킬 수 있기 때문이다.그러나 4극 이상의 모멘트만이 중력을 방출할 수 있다.질량 단극은 보존된 시스템의 총 질량 에너지를 나타내므로 방사선을 방출하지 않는다.마찬가지로 질량 쌍극자는 시스템의 질량 중심에 해당하며, 그 첫 번째 도함수는 운동량을 나타내며, 운동량은 보존량이기 때문에 질량 쌍극자도 방사선을 방출하지 않는다.그러나 질량 4극은 시간에 따라 변할 수 있으며, 중력 ^[5]복사에 가장 낮은 차수의 기여를 한다.

복사 시스템의 가장 단순하고 중요한 예는 원형 궤도에서 서로 공전하는 동일한 질량을 가진 한 쌍의 질량점으로, 예를 들어 이진 블랙홀의 특수한 경우에 근접한 것이다.쌍극자 모멘트가 일정하기 때문에 두 점 사이에 좌표 원점을 배치할 수 있습니다.그러면 쌍극자 모멘트는 0이 될 것이고, 만약 우리가 점들이 중앙으로부터 반대 방향으로 단위 거리에 있도록 좌표들을 스케일링한다면, 시스템의 4극 모멘트는 단순하게 될 것입니다.

({displaystyle Q_{i}=M\left(3x_i}x_{j}-\mathbf {x}^{2}\display_{ij}\right)}

여기서 M은 각 점의 $x_{i}$ 이고 $(\$ })는 $x_{i}$ 점 중 하나의 (단위) 위치 벡터의 구성요소입니다.이들이 궤도를 돌면서 이 x 벡터는 회전합니다. 즉, 0이 아닌 첫 번째 시간 도함수를 가지며 두 번째 시간 도함수를 갖습니다(이것은 물론 좌표계의 선택에 관계없이 해당됩니다).그러므로 이 시스템은 중력파를 방출할 것이다.이러한 방식으로 손실된 에너지는 비슷한 질량의 다른 중성자별이 있는 궤도상의 펄서인 헐스-테일러 쌍성의 변화 주기에서 처음 추론되었다.

전하와 전류 다중극이 전자기장에 기여하는 것처럼, 질량과 질량 전류 다중극은 일반 상대성 이론에서 중력장에 기여하며, 소위 중력 자기 효과를 유발합니다.질량 전류 다중극의 변화도 중력 복사를 방출할 수 있다.그러나 현재 다중극의 기여는 일반적으로 질량 4극의 기여보다 훨씬 작을 것이다.

「」를 참조해 주세요.

레퍼런스

^ Applequist, J. (1989). "Traceless cartesian tensor forms for spherical harmonic functions: New theorems and applications to electrostatics of dielectric media". Journal of Physics A: Mathematical and General. 22 (20): 4303–4330. Bibcode:1989JPhA...22.4303A. doi:10.1088/0305-4470/22/20/011.
^ Weisstein, Eric. "Electric Quadrupole Moment". Eric Weisstein's World of Physics. Wolfram Research. Retrieved May 8, 2012.
^ Jackson, John David (1975). Classical Electrodynamics. John Wiley & Sons. ISBN 0-471-43132-X.
^ Griffiths, David J. (2013). Introduction to Electrodynamics, 4th ed. Pearson. p. 153,165.
^ Thorne, Kip S. (April 1980). "Multipole Expansions of Gravitational Radiation" (PDF). Reviews of Modern Physics. 52 (2): 299–339. Bibcode:1980RvMP...52..299T. doi:10.1103/RevModPhys.52.299.

외부 링크

다극 확장

[1] Applequist, J. (1989). "Traceless cartesian tensor forms for spherical harmonic functions: New theorems and applications to electrostatics of dielectric media". Journal of Physics A: Mathematical and General. 22 (20): 4303–4330. Bibcode:1989JPhA...22.4303A. doi:10.1088/0305-4470/22/20/011.

[wolf_eqm-2] Weisstein, Eric. "Electric Quadrupole Moment". Eric Weisstein's World of Physics. Wolfram Research. Retrieved May 8, 2012.

[3] Jackson, John David (1975). Classical Electrodynamics. John Wiley & Sons. ISBN 0-471-43132-X.

[4] Griffiths, David J. (2013). Introduction to Electrodynamics, 4th ed. Pearson. p. 153,165.

[5] Thorne, Kip S. (April 1980). "Multipole Expansions of Gravitational Radiation" (PDF). Reviews of Modern Physics. 52 (2): 299–339. Bibcode:1980RvMP...52..299T. doi:10.1103/RevModPhys.52.299.

[1]

[2]

[3]

[4]

[5]

Search

사극

네임스페이스

더

목차

수학적 정의

전기 사중극

일반화: 멀티폴이 높음

자기 사극

중력 사극

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

사극

수학적 정의

전기 사중극

일반화: 멀티폴이 높음

자기 사극

중력 사극

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.