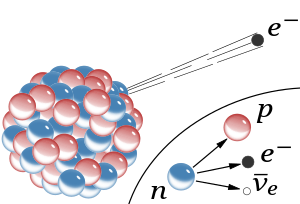
자유 중성자 붕괴

원자핵에 내장되어 있을 때 중성자는 (보통) 안정된 입자다. 핵 외부에서는 자유 중성자가 불안정하며 평균 수명은 879.6±0.8초(약 14분, 39.6초)이다.^[1] 따라서 이 프로세스의 반감기(ln(2) ≈ 0.693의 인수로 평균 수명과는 다름)는 611±1초(약 10분, 11초)이다.^[2][3] (2021년 10월에 발표된^[4] 기사는 평균 수명 동안 877.75+0.50-0
.44s에 도달한다.)

이 글에서 설명한 중성자의 베타 붕괴는 아래 섹션의 파인만 다이어그램의 4개 층에서 볼 수 있듯이 약간 다른 4개의 세부 수준에서 설명될 수 있다.

n^0
+
→ p + e + ν
⁻

_e

관찰하기 어려운 W는
⁻
전자와 일치하는 안티뉴트리노로 빠르게 분해된다. 바로 위에 나타난 아원자 반응은 20세기 전반기에 처음 이해되었던 과정을 묘사한다. 보손(W⁻
)은 너무 빨리 사라져서 훨씬 뒤에야 감지되었다. 후에 베타 붕괴는 때로는 충전된 약한 전류라고 불리는 약한 보손(W^±
)의 방출에 의해 발생하는 것으로 이해되었다. 베타 붕괴는 특히 중성자 안에 숨겨진 다운 쿼크 중 하나에서 W
⁻
보슨이 방출되어 다운 쿼크를 업 쿼크로 변환하고 결과적으로 중성자를 양성자로 변환시키는 것을 포함한다. 다음 도표는 현재 이해 수준에 따른 베타 붕괴 프로세스의 요약 스케치를 제공한다.

3 쿼크 복합 중성자(n0 )		3 쿼크 복합 양성자(p+ )
︷		︷
( u d d )	→	( 우두 )	+	W−
				⤷	e−		+ ν e
				︸
				그 후의 W− 썩다

굵은
(d
)로 표시된 다운 쿼크는 명목상 보손(W⁻
)을 방출하여 업 쿼크(
u
)로 변화하며, 또한 볼드체로도 나타난다. 볼드체로 표시되지 않은 ud


쿼크 쌍은 전체 이벤트에 대한 불활성 방관자.

몇 가지 세부 수준의 다이어그램에 대한 내용은 아래 § 붕괴 프로세스를 참조하십시오.

에너지예산

자유 중성자의 경우 이 공정(중성자, 양성자 및 전자의 나머지 질량 기준)에 대한 붕괴 에너지는 0.782343 MeV이다. 그것이 중성자의 나머지 질량과 생산물의 나머지 질량의 합계의 차이다. 그 차이는 운동 에너지로 옮겨져야 한다. 베타 붕괴 전자( 중성미자가 소멸할 정도로 적은 양의 운동에너지를 받는 과정에서)의 최대 에너지는 0.782±0.013 MeV로 측정되었다.^[5] 후자의 숫자는 중성미자의 비교적 작은 휴식 질량(이론적으로 최대 전자 운동 에너지에서 빼야 함)을 결정하기 위해 잘 측정되지 않는다. 더욱이 중성미자 질량은 많은 다른 방법에 의해 제한된다.

소분수(약 1/1/1000)의 자유 중성자가 동일한 산물로 부패하지만, 방출 감마선 형태의 추가 입자를 추가하는 경우:

n⁰
→ p⁺
+ e⁻
+ ν
_e + γ + γ

이 감마선은 방출된 베타 입자(전자)가 전자파 방식으로 양성자의 전하와 상호작용하면서 발생하는 일종의 "내부 브렘스트라룽"으로 생각할 수 있다. 이 과정에서 일부 붕괴 에너지는 광자 에너지로 운반된다. 이러한 방식으로 생성된 감마선은 결합 중성자, 즉 핵 내의 베타 디케이드의 작은 특징이기도 하다.

중성자 디케이의 극소수(약 4백만 개)는 이른바 '두 몸(중성자) 디케이즈'로 양성자, 전자, 안티뉴트리노가 평상시처럼 생산되지만 전자가 양성자(수소의 이온화 에너지)를 탈출하는 데 필요한 13.6 eV의 에너지를 얻지 못하여 중성자 디케이트로서 간단히 그것에 묶여 있다.이드로겐 원자("두 개의 몸" 중 하나) 이러한 유형의 자유 중성자 붕괴에서 본질적으로 모든 중성자 붕괴 에너지는 안티뉴트리노(다른 "몸")에 의해 이동된다.

자유 중성자가 자유 양성자보다 질량이 크기 때문에 자유 양성자의 중성자(양전자, 중성자 포함)로의 변환은 정력적으로 불가능하다.^{[citation needed]} 그러나 양성자의 부패를 보라.

여러 수준에서 본 붕괴 프로세스

엔리코 페르미와 동료들에 대한 초기 이해는 아래 다이어그램의 "초상적인" 첫 번째 수준에서 시작되면서, 베타 붕괴 과정에 대한 이해는 몇 년 동안 발전했다. 약한 공정에 대한 현재의 이해는 차트의 하단에서 핵(중성자와 그 후속 양성자)이 대부분 무시되고, 주의는 두 쿼크와 충전된 보손 사이의 상호작용에만 초점을 맞추고, 보손의 붕괴는 거의 사후사고로 취급된다. 충전된 약한 보손(
W⁻
)은 그렇게 빨리 사라지기 때문에, 20세기 전반에는 실제로 관찰되지 않았기 때문에, 레벨 1의 도표는 그것을 생략하고, 현재까지도 그것의 후유증으로 유추되는 대부분의 부분이다.

1 피상 BARYON 레벨
n0	→	p+	+		e−		+ ν e		중성자( n0 )는 전자( e− )와 그 안티뉴트리노( ν e)를 방출하여 양성자( p+ )가 된다.
2 더 깊은 BOSON 레벨
n0	→	p+		+ − W					중성자( n0 )는 W보손을− 방출하여 양성자(p)가+ 된다.
				⤷	e−		+ ν e		W− 보슨은 전자( e− )와 그 안티뉴트리노( ntineutrino e)로 분해된다.
3 더 깊은 NucleON 수준
( u d d )	→	( 우두 )	+	W−					중성자의 다운 쿼크 중 하나가 W 보슨을 − 방출하여 업 쿼크가 된다.
				⤷	e−		+ ν e		W− 보슨은 전자( e− )와 그 안티뉴트리노( ntineutrino e)로 분해된다.
4 깊은 QUARK 레벨
d	→	u	+	W−					다운 쿼크( d )는 W− 보슨을 방출하고 업 쿼크(u )가 된다.
				⤷	e−		+ ν e		W− 보슨은 전자( e− )와 그 안티뉴트리노( ntineutrino e)로 분해된다.

중성자 수명 퍼즐

중성자 수명은 수십 년 동안 연구되어 왔지만, 현재 두 가지 실험 방법("보틀" 대 "빔")과의 다른 결과 때문에 정확한 값에 대한 합의성이 부족하다.^[6][a] "중성자 수명 이상"은 초경량 중성자를 사용한 실험이 정교해진 후에 발견되었다.^[7] 오류 마진이 한때 겹치기도 했지만, 문제를 해결했어야 할 기술 개선의 증가는 단일 가치로 수렴하는 것을 보여주지 못했다.^{[8][9][10][11]} 2014년 현재 얻은 평균 수명 값의 차이는 약 9초였다.^[9] 또한 2018년 현재 양자 색역학을 기반으로 한 값의 예측은 여전히 한 가지를 서로 지지하기에 충분히 정확하지 않다.^[12][b] 월초버(2018년)가 설명한 것처럼 양성자를 생성하지 않는 붕괴 모드가 있다면 빔 테스트는 부정확할 수 있다.^[6]

1310월 2021년에는 병법에서 평생 nτ)877.75 s{\displaystyle \tau_{n}=877.75s}887.7 s{\displaystyle \tau_{n}=887.7s}[14][15] 소설 세번째 메서드는 지난 나 후보로부터 데이터를 사용하 τ n의 탐상 법 값 10초 탭 아래의, 또한 같은 날짜에 관한 차이가 증가되고 있[13][4]업데이트되었습니다.sa의 달 pros벡터 미션은 ${\displaystyle {missionn}_{}}$= ${\displaystyle \mathrm{887s}}$ ${\displaystyle \tau _{n}=887s}$의^[16][17] 값을 보고했지만 매우 불확실했다.

그러나 일본프로톤가속기 연구단지(J-PARC)와 빔 방식과 유사한 또 다른 접근방식이 모색되었지만, 이 차이를 분석하는데 있어 현재로선 너무 부정확하다.^[18][19]

참고 항목

• "bottle" 방법에 사용되는 Halbach 배열

각주

참조

참고 문헌 목록

• Ерозолимский, Б.Г. [Yerozolimskiy, B.G.] (1975). "Бета-распад нейтрона" [Neutron beta decay]. Успехи физических наук [Advances in Physics]. 116 (1): 145–164.{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크)