퍼지 제어 시스템

이 글은 일반적인 참고문헌 목록을 포함하고 있지만, 그에 상응하는 인라인 인용구가 충분하지 않기 때문에 대체로 검증되지 않은 상태로 남아 있다. 좀 더 정밀한 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오. (2011년 5월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

이 글은 교과서처럼 읽힌다. 이 글을 개선하여 어조가 중립적이고 위키백과의 품질 기준을 충족시키십시오. (2010년 2월)

퍼지 제어 시스템은 퍼지 논리 기반의 제어 시스템 - 고전적 또는 디지털 논리(각각 참 또는 거짓)와 대조적으로 0과 1 사이의 연속적인 값을 갖는 논리적 변수의 관점에서 아날로그 입력 값을 분석하는 수학 시스템이다.^[1][2]

개요

퍼지 논리는 기계 제어에 널리 사용된다. '퍼지(fuzzy)'라는 용어는 관련 논리가 '진실'이나 '거짓'으로 표현될 수 없고 오히려 '부분적으로 진실'이라고 표현될 수 있는 개념을 다룰 수 있다는 사실을 가리킨다. 유전 알고리즘이나 신경망과 같은 대안적 접근방식이 많은 경우 퍼지 논리만큼 잘 수행될 수 있지만 퍼지 논리는 인간 운영자가 이해할 수 있는 용어로 문제에 대한 해결책을 던져 그들의 경험이 제어기의 설계에 이용될 수 있다는 장점이 있다. 이로써 이미 인간이 성공적으로 수행하고 있는 작업을 기계화하기가 쉬워진다.^[1]

기록 및 응용 프로그램

퍼지 논리는 1965년 논문에서 버클리 캘리포니아 대학의 로피 A. 자데에 의해 제안되었다.^[3] 그는 1973년 논문에서 "언어적 변수"라는 개념을 도입한 자신의 생각을 상세히 설명했는데, 이 논문에서는 퍼지 집합으로 정의된 변수를 동일시한다. 다른 연구가 뒤따랐는데, 덴마크에 건설된 최초의 산업용 가마가 1975년에 출시되었다.

퍼지 시스템은 처음에 일본에서 시행되었다.

• 퍼지 시스템에 대한 관심은 1985년 센다이 지하철의 퍼지 제어 시스템의 실현 가능성을 입증하는 시뮬레이션을 제공했던 히타치의 야스노부 세이지와 미야모토 소지에 의해 촉발되었다. 그들의 사상은 채택되었고 1987년 남보쿠선이 개통되었을 때 가속, 제동, 정지 등을 제어하기 위해 퍼지 시스템이 사용되었다.
• 1987년 야마카와 다케시는 "반전 진자" 실험에서 단순한 전용 퍼지 논리 칩 세트를 통해 퍼지 제어의 사용을 시연했다. 차량이 앞뒤로 움직여 경첩에 의해 상부에 장착된 폴을 그대로 유지하려 하는 고전적인 제어장치 문제다. 야마카와 교수는 이어 물이 담긴 와인잔과 심지어 생쥐까지 진자의 꼭대기에 장착함으로써 시연을 더욱 정교하게 만들었다. 즉, 시스템은 두 경우 모두에서 안정성을 유지했다. 야마카와 씨는 결국 자신의 특허를 이 분야에서 활용하도록 돕기 위해 퍼지 시스템 연구소를 조직했다.
• 일본 엔지니어들은 그 후 산업용과 소비자용 애플리케이션 모두를 위한 광범위한 퍼지 시스템을 개발했다. 1988년, 일본은 퍼지 연구를 추진하기 위해 48개 회사들 간의 협력적인 협정인 국제 퍼지 엔지니어링 연구소를 설립했다. 자동차 회사인 폭스바겐은 3년 동안 연구원을 파견해 유일하게 LIFE의 외국 법인회원으로 활동했다.
• 일본 소비재는 종종 퍼지 시스템을 포함한다. 마츠시타 진공청소기는 퍼지 알고리즘을 실행하는 마이크로컨트롤러를 사용하여 먼지 센서를 조사하고 그에 따라 흡입력을 조절한다. 히타치 세탁기는 퍼지 컨트롤러를 사용하여 무게, 패브릭믹스, 먼지 센서를 적재하고 전력, 물, 세제를 최적으로 사용할 수 있도록 세탁 주기를 자동으로 설정한다.
• 캐논은 CCD(Charge Coupled Device)를 이용해 시야의 6개 영역에서 이미지 선명도를 측정하고 제공된 정보를 활용해 이미지가 초점인지 판단하는 자동집중 카메라를 개발했다. 초점중 렌즈 이동 변화율도 추적하고, 오버슈트 방지를 위해 속도를 조절한다. 카메라의 퍼지 제어 시스템은 CCD가 제공하는 현재 명료성 데이터를 얻기 위해 6개, 렌즈 이동의 변화 속도를 측정하기 위해 6개 등 12개의 입력을 사용한다. 출력은 렌즈의 위치다. 퍼지 제어 시스템은 13개의 규칙을 사용하며 1.1킬로바이트의 메모리를 요구한다.
• 미쓰비시가 설계한 산업용 에어컨은 난방법 25개와 냉방법 25개를 사용한다. 온도 센서는 인버터, 컴프레서 밸브 및 팬 모터로 공급되는 제어 출력과 함께 입력을 제공한다. 기존 설계에 비해 퍼지 컨트롤러는 가열 및 냉각 속도가 5배 빨라지고, 전력 소비량이 24% 감소하며, 온도 안정성이 2배 증가하며, 센서 사용량이 적다.
• 조사 또는 구현된 다른 애플리케이션으로는 문자 및 필적 인식, 광학적 퍼지 시스템, 일본 꽃꽂이를 위한 로봇, 음성 제어 로봇 헬리콥터(호빙은 역진자와 유사한 "균형법"), 환자에 특정한 기능을 제공하기 위한 재활 로봇 등이 있다.올리브(예: 심박수 및 혈압 조절), 필름 제조 시 분말 흐름 제어, 엘리베이터 시스템 등

퍼지 시스템에 대한 작업은 일본보다 덜 광범위한 규모지만 북미와 유럽에서도 진행되고 있다.

• 미국 환경보호국은 에너지 효율이 높은 모터에 대한 퍼지 제어를 조사했고 NASA는 자동화된 우주 도킹에 대한 퍼지 제어를 연구했다: 퍼지 제어 시스템이 연료 소비를 크게 줄일 수 있다는 것을 알 수 있다.
• 보잉, 제너럴 모터스, 앨런-브래들리, 크라이슬러, 이튼, 월풀과 같은 회사들은 저전력 냉장고, 개선된 자동차 변속기, 그리고 에너지 효율적인 전기 모터에 사용하기 위한 퍼지 논리 작업을 해왔다.
• 1995년 메이태그는 퍼지 제어기를 기반으로 한 '지능형' 식기세척기와 온도측정을 위해 서미스터를 결합한 '원스톱 센싱 모듈', 세탁물에 존재하는 이온에서 나오는 세제 수준을 측정하기 위한 전도도 센서, 산란되고 전송된 빛을 측정하여 오염도를 측정하는 탁도 센서 등을 도입하였다. 세차; 그리고 회전 속도를 판독하기 위한 자기 자극 센서. 시스템은 최소한의 에너지, 세제 및 물로 최상의 결과를 얻기 위해 모든 하중에 대한 최적의 세척 주기를 결정한다. 심지어 마지막으로 문을 연 시간을 추적해 건조식품에 맞춰 조절하고, 문을 연 횟수로 접시 수를 추정한다.
• 2017년에 Xiera Technologies Inc.는 edeX로 알려진 퍼지 논리 제어기의 지식 기반을 위한 최초의 오토 튜너를 개발했다. 이 기술은 모호크 칼리지가 시험한 것으로 비선형 2x2와 3x3 멀티입력 멀티출력 문제를 해결할 수 있었다.^[5]

또한 "자기 학습" 퍼지 제어 시스템 구축이라는 궁극적인 목표를 가지고, 퍼지 전문가 시스템과 신경망 및 소위 적응형 "유전자적" 소프트웨어 시스템과의 퍼지 로직 통합 및 퍼지 로직의 통합을 포함하여, 펌웨어와 반대로, 설계와 달리 소프트웨어의 퍼지 애플리케이션에 대해서도 연구와 개발이 계속되고 있다.^[6] 이러한 시스템은 예를 들어 인체처럼 복잡하고 비선형적인 동적 식물을 제어하기 위해 사용될 수 있다.^[7][4][6][8]

퍼지 집합

퍼지 제어 시스템의 입력 변수는 일반적으로 "퍼지 집합"이라고 알려진 이와 유사한 구성원 자격 함수의 집합에 의해 매핑된다. 아삭아삭한 입력값을 퍼지 값으로 변환하는 과정을 "퍼지화"라고 한다. 퍼지 논리 기반 접근방식은 두 개의 퍼지 시스템(오류 머리글 각도와 속도 제어용)을 설계함으로써 고려되었다.^[9]

제어 시스템은 아날로그 입력과 함께 다양한 유형의 스위치 또는 "ON-OFF" 입력을 가질 수 있으며, 그러한 스위치 입력은 물론 항상 1 또는 0과 동일한 진실 값을 가질 수 있지만, 체계는 한 가지 값 또는 다른 값인 단순 퍼지 함수로 처리할 수 있다.

마이크로컨트롤러는 입력 변수의 "매핑"을 멤버십 함수와 진리 값으로 지정하면, 각 형식에 기초하여 "규칙"의 집합에 기초하여 어떤 조치를 취해야 할지에 대한 결정을 내린다.

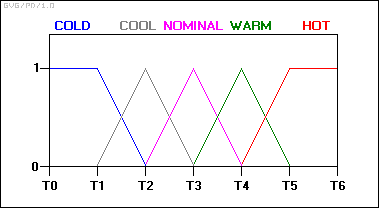
  브레이크 온도가 따뜻하고 속도가 그리 빠르지 않으면 브레이크 압력이 약간 감소한다.  

이 예에서 두 입력 변수는 퍼지 집합으로 정의된 값을 갖는 "브레이크 온도"와 "속도"이다. 출력 변수인 "브레이크 압력"은 "정적" 또는 "약간 증가" 또는 "약간 감소" 등과 같은 값을 가질 수 있는 퍼지 집합에 의해서도 정의된다.

퍼지 제어 세부 정보

퍼지 컨트롤러는 개념적으로 매우 단순하다. 입력 단계, 처리 단계, 출력 단계로 구성된다. 입력 스테이지 센서 또는 스위치, 섬휠 등과 같은 기타 입력을 적절한 멤버십 기능과 진실 값으로 매핑한다. 처리 단계는 각각의 적절한 규칙을 호출하고 각 규칙에 대한 결과를 생성한 다음 규칙의 결과를 결합한다. 마지막으로 출력 단계는 결합된 결과를 다시 특정 제어 출력 값으로 변환한다.

멤버십 함수의 가장 일반적인 모양은 삼각형이지만 사다리꼴과 종곡선도 사용되지만, 모양은 일반적으로 곡선의 수와 위치보다 덜 중요하다. 3개에서 7개까지의 곡선은 일반적으로 입력값의 필요한 범위 또는 퍼지 전문 용어로 "담론의 단일우주"를 포함하기에 적절하다.

앞에서 논의한 바와 같이, 처리 단계는 IF-TEN 문장의 형태로 논리 규칙의 집합에 근거하고 있는데, 여기서 IF 부분은 "선행자"라고 하고, DEN은 "후속자"라고 한다. 전형적인 퍼지 제어 시스템은 수십 가지의 규칙을 가지고 있다.

온도 조절기의 규칙을 고려하십시오.

  IF(온도가 "콜드"인 경우) 회전(히터가 "하이"인 경우) 

이 규칙은 "콜드"의 일부 진리 값인 "온도" 입력의 진리 값을 사용하여 "히터" 출력에 대한 퍼지 집합의 결과를 생성하는데, 이것은 "하이"의 일부 값이다. 이 결과는 다른 규칙의 결과와 함께 사용되어 최종적으로 선명한 복합 출력을 생성한다. 분명히, "콜드"의 진리 값이 클수록 "하이"의 진리 값이 더 높아지지만, 이것이 많은 것 중 하나의 규칙이기 때문에 반드시 출력 자체를 "하이"로 설정한다는 것을 의미하지는 않는다. 멤버십 함수는 부사에 해당하는 '헤지'로 수정할 수 있는 경우도 있다. 일반적인 위험회피에는 "정보", "근접", "근접", "근접", "약간", "매우", "조금", "투", "극히" 및 "어느 정도"가 포함된다. 이러한 운영에는 정확한 정의가 있을 수 있지만, 구현마다 정의가 상당히 다를 수 있다. 예를 들어, "매우"는 사각형 구성원 자격 함수를 의미한다. 구성원 자격 값이 항상 1보다 작기 때문에, 이것은 구성원 자격 함수의 범위를 좁힌다. "극히"는 값을 정사각형으로 하여 더 크게 좁혀지는 반면, "어떤 것"은 제곱근을 취함으로써 기능을 넓힌다.

실제로 퍼지 규칙 집합은 일반적으로 AND, OR 및 NOT와 같은 퍼지 연산자를 사용하여 결합되는 몇 개의 선행 조건을 가지고 있지만, 다시 정의는 달라지는 경향이 있다: AND, 하나의 일반적인 정의에서 모든 선행 조건의 최소 가중치를 사용하는 반면, OR은 최대값을 사용한다. 1에서 멤버십 함수를 빼서 "완성" 함수를 주는 NOT 연산자도 있다.

규칙의 결과를 정의하는 방법에는 여러 가지가 있지만, 가장 보편적이고 간단한 방법 중 하나가 "max-min" 추론 방법인데, 출력 멤버십 함수에 전제가 생성되는 진리 값이 주어진다.

규칙은 하드웨어에서 병렬로, 또는 소프트웨어에서 순차적으로 해결할 수 있다. 발사된 모든 규칙의 결과는 몇 가지 방법 중 하나에 의해 "방어(defuzzed)"된 값으로 선명하게 평가된다. 이론적으로는 각각 다양한 장점과 단점을 가진 수십 개가 있다.

결과의 「질량의 중심」이 바삭바삭한 값을 제공하는 「중심」 방식이 매우 인기 있다. 또 다른 접근법은 가장 큰 기여자의 가치를 취하는 "높이" 방법이다. 중심 방법은 가장 큰 면적의 출력을 가진 규칙을 선호하지만, 높이 방법은 분명히 가장 큰 출력 값을 가진 규칙을 선호한다.

아래 다이어그램은 입력 변수 "x", "y" 및 "z"와 출력 변수 "n"이 있는 시스템의 최대 회의 및 중심 디퍼지화를 보여준다. "mu"는 "진실 값"에 대한 표준 퍼지 로직 명명법이라는 점에 유의하십시오.

각 규칙이 출력 변수에 대한 특정 구성원 자격 함수의 진실 값으로 결과를 제공하는 방법에 주목하십시오. 중심 부호화에서 값은 OR'd, 즉 최대값을 사용하고 값을 추가하지 않은 다음 중심 계산을 사용하여 결과를 조합한다.

퍼지 제어 시스템 설계는 경험적 방법, 기본적으로 시행착오에 대한 방법론적 접근법에 기초한다. 일반적인 과정은 다음과 같다.

• 시스템의 작동 사양과 입력 및 출력을 문서화한다.
• 입력에 대한 퍼지 집합을 문서화하십시오.
• 규칙 집합을 문서화하십시오.
• 제습 방법을 결정한다.
• 테스트 제품군을 실행하여 시스템 유효성을 확인하고 필요에 따라 세부 정보를 조정하십시오.
• 문서 작성 및 프로덕션에 릴리스

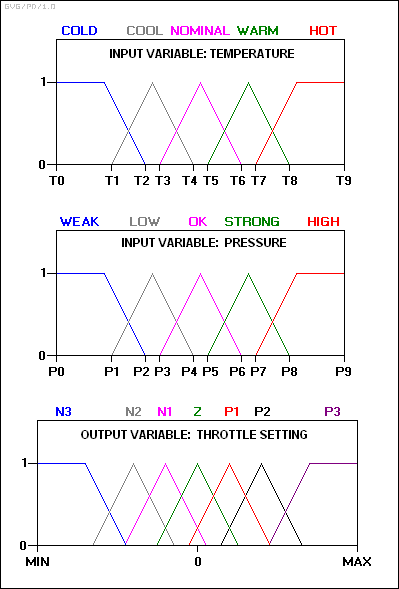
일반적인 예로서 증기 터빈에 대한 퍼지 제어기의 설계를 고려한다. 이 제어 시스템의 블록 다이어그램은 다음과 같이 나타난다.

입력 및 출력 변수는 다음과 같은 퍼지 집합에 매핑된다.

—어디서:

  N3: 큰 음수.   N2: 중간 음수.   N1: 작은 음수.   Z: 제로.   P1: 작은 양수.   P2: 중간 양수.   P3: 양성이 크다.  

규칙 집합에는 다음과 같은 규칙이 포함된다.

규칙 1: 온도가 냉각되고 압력이 약하면 스로틀은 P3이다.  

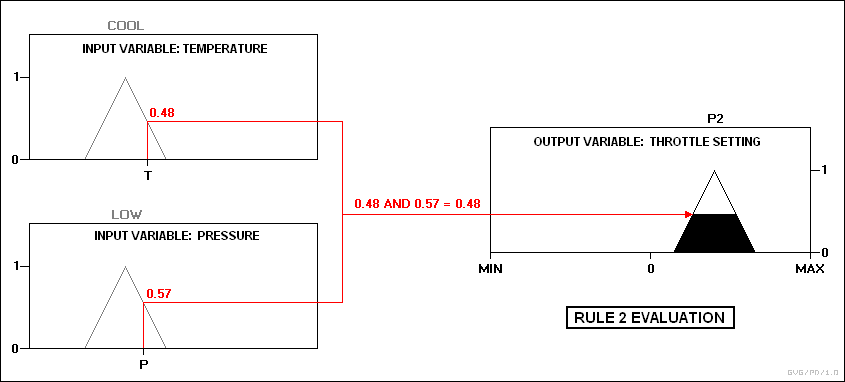
규칙 2: 온도가 냉각되고 압력이 낮으면 스로틀은 P2가 된다.  

규칙 3: 온도가 냉각되고 압력이 정상이면 스로틀은 Z가 된다.  

규칙 4: 온도가 냉각되고 압력이 강하면 스로틀은 N2가 된다. 

실제로, 컨트롤러는 입력을 받아들여 회원 기능 및 진실 값에 매핑한다. 그리고 나서 이 지도들은 규칙으로 보내진다. 규칙이 위의 예처럼 두 입력 변수의 매핑 사이의 AND 관계를 지정하는 경우, 둘 중 최소값을 결합 진리 값으로 사용하고, OR을 지정하면 최대값을 사용한다. 전제의 진실 수준에서 적절한 출력 상태를 선택하고 멤버십 값을 할당한다. 그리고 나서 진실의 가치는 더럽혀진다. 예를 들어 온도가 "냉각" 상태이고 압력이 "낮음" 및 "확인" 상태라고 가정하십시오. 압력 값은 화재 규칙 2와 3만 보장한다.

그런 다음 두 출력은 중심 탈부착을 통해 탈부착된다.

   ______________________________________________ Z P2 1 -+ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *                                                *     * *     *                                               *       222222222                                              *       22222222222                                             333333332222222222222                                        +---33333333222222222222222-->                                                         ^                                                        +150     __________________________________________________________________ 

출력 값은 스로틀을 조정하고 제어 사이클을 다시 시작하여 다음 값을 생성한다.

퍼지 컨트롤러 구축

마이크로컨트롤러 칩을 사용하여 다음과 같은 간단한 피드백 컨트롤러를 구현해 보십시오.

퍼지 집합은 입력 오류 변수 "e"와 파생된 오류 변화 "델타" 및 "출력"에 대해 다음과 같이 정의된다.

  LP: 큰 양의 SP: 작은 양의 ZE: 0 SN: 작은 음의 LN: 큰 음의 

오류 범위가 -1 ~ +1이고, 아날로그-디지털 변환기의 분해능이 0.25인 경우, 입력 변수의 퍼지 집합(이 경우 출력 변수에도 적용됨)은 매우 간단하게 표로 설명할 수 있으며, 상단 행의 오류/델타/출력 값과 각 멤버십 함수에 대한 진실 값을 표로 설명할 수 있다.아래 줄에 nged:

  _______________________________________________________________________                -1    -0.75  -0.5   -0.25    0     0.25   0.5    0.75    1   _______________________________________________________________________     mu(LP)      0      0      0      0      0      0     0.3    0.7     1    mu(SP)      0      0      0      0     0.3    0.7     1     0.7    0.3    mu(ZE)      0      0     0.3    0.7     1     0.7    0.3     0      0    mu(SN)     0.3    0.7     1     0.7    0.3     0      0      0      0    mu(LN)      1     0.7    0.3     0      0      0      0      0      0   _______________________________________________________________________            —or, in graphical form (where 각 "X"의 값은 0.1이다. 

         LN SN ZE SP LP +------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------            : -0.5 XXXXXXXXXXXXXXXXX : -0.25 : XXXXXXXXXXXX : 0.0 : XXXXXXXXXXXX : 0.25 : XXXXXXXXXXXXXXXXXXXXXXXX : 0.5 : XXXXXXXXXXXXXX : : : XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX : : : : : : :XXXXXXXXXXXXXX 0.75 : : XXXXXXXXXX 1.0 : XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX 

이 퍼지 시스템에 다음과 같은 규칙 기반이 있다고 가정해 보십시오.

  규칙 1: e = ZE AND 델타 = ZE 출력 = ZE 규칙 2: IF e = ZE AND 델타 = SP: SN 규칙 3: IF e = SN 및 델타 = SN 출력 = LP 규칙 4: IF e = LP 또는 델타 = LP 출력 = LP = LP 출력 = LP 출력 = LP = LP 출력 = LP 

이러한 규칙은 선행 조건이 오류와 오류-델타 신호의 논리적 조합으로 구성되는 반면, 그 결과는 제어 명령 출력이라는 점에서 제어 애플리케이션에 일반적으로 적용된다. 규칙 출력은 이산 중심 연산을 사용하여 제거할 수 있다.

  SUM(I = 1 TO 4 of (mu(I) * 출력(I) ) / SUM(I = 1 TO 4 of mu(I) ) 

자, 주어진 시간에 다음과 같이 가정해보자.

  e = 0.25 델타 = 0.5 

그러면 다음과 같은 이점을 얻을 수 있다.

  _________________________________________ 0.3 mu(SN) 0.3 mu(SN) 0 0(_______________________________________________________________________________________ 

규칙 1에 연결하면 다음이 제공됨:

  규칙 1: e = ZE AND 델타 = ZE 출력 = ZE mu(1) = MIN(0.7, 0.3 ) = 0.3 출력(1) = 0 

-- 여기서:

• mu(1): 규칙 1에 대한 결과 구성원 자격 함수의 진실 값. 중심 계산의 관점에서, 이것은 이 이산형 사례에 대한 이 결과의 "질량"이다.
• output(1): 결과 멤버십 함수(ZE)가 출력 변수 퍼지 집합 범위보다 최대인 값(규칙 1) 즉, 중심 계산의 관점에서, 이 개별 결과에 대한 "질량의 중심"의 위치인 것이다. 이 값은 "mu"의 가치와 무관하다. 단순히 출력 범위를 따라 ZE의 위치를 파악한다.

다른 규칙은 다음과 같다.

  규칙 2: e = ZE AND 델타 = SP인 경우 출력 = SN mu(2) = MIN(0.7, 1 ) = 0.7 출력(2) = -0.5 

  규칙 3: e = SN AND 델타 = SN 출력 = LP mu(3) = MIN(0.0, 0.0 ) = 0 출력(3) = 1 

  규칙 4: e = LP OR 델타 = LP이면 출력 = LN mu(4) = MAX(0.0, 0.3 ) = 0.3 출력(4) = -1 

중심 계산 산출량:

 ${\displaystyle {\frac {mu(1)\cdot output(1)+mu(2)\cdot output(2)+mu(3)\cdot output(3)+mu(4)\cdot output(4)}{mu(1)+mu(2)+mu(3)+mu(4)}}}$ ${\displaystyle =\frac{(0.3\cdot 0)+(0}{}}$${\displaystyle ={\frac {(0.3\cdot 0)+(0.7\cdot -0.5)+(0\cdot 1)+(0.3\cdot -1)}{0.3+0.7+0+0.$$3$${\displaystyle }$ =${\displaystyle \mathrm{}}$- ${\displaystyle 0}$.5 ${\displaystyle =-0.5$최종 제어 출력용. 간단하다. 물론 어려운 부분은 실제로 어떤 규칙이 실제로 제대로 작동하는지 알아내는 것이다.  

중심 방정식을 알아내는 데 문제가 있는 경우 중심은 무게 중심 주위의 모든 모멘트(위치 시간 질량)를 합산하고 합을 0과 동일시하여 정의된다는 점을 기억하십시오. 따라서 $X{\displaystyle {}_{}}$ ${\$이 중력의 중심이고, ${\displaystyle X_{}}$ i ${\$이 각 중량의 위치이고, ${\displaystyle {Mi}_{}}$ ${\$이 각 중량의 중심이라면, 이것은 다음을 제공한다.

  ${\displaystyle 0=(X_{1}-X_{0})\cdot M_{1}+(X_{2}-X_{0})\cdot M_{1}+(X_{n}-X_{0})\cdot M_{n}}}}}}$   ${\displaystyle 0=(X_{1}\cdot M_{1}+X_{2}\cdot M_{2}+\ldots +X_{n}\cdot M_{n}}-X_{0}-X_{0}-{1}+M_{2}+\ldots+{n}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.$   ${\displaystyle X_{0}\cdot(M_{1}+{2}+\ldots +{n})=X_{1}\cdot M_{1}+{1}X_{2}+{{2}+}\cdots +X_{n}}\cdot M_{n}}}}}}}}}}}}}}}}}}}}}}.$   ${\displaystyle X_{0}={\frac {X_{1}\cdot M_{1}+{1}+X_{2}+}\cdot M_{2}+\ldots +X_{n}}}}{M_{1}+M_{1}+}+{n}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$ 

본 예에서 mu의 값은 질량에 대응하며, 질량의 위치에 대한 X의 값(그러나 출력함수의 초기 '질량'이 모두 동일/등가인 경우에는 '질량에 대응한다'는 것에 불과하다. 만약 그것들이 같지 않다면, 즉, 어떤 것은 좁은 삼각형이고, 반면에 다른 것은 넓은 사다리꼴이나 쐐기 모양의 삼각형일 경우, 출력 함수의 질량이나 면적을 알거나 계산해야 한다. mu에 의해 스케일링되고 위치 X_i)에 곱한 것이 바로 이 질량이다.

이 시스템은 표준 마이크로프로세서에서 구현될 수 있지만, 전용 퍼지 칩은 현재 사용할 수 있다. 예를 들어 캘리포니아주 산호세의 Adaptive Logic INC는 4개의 아날로그 입력을 받아들이고 4개의 아날로그 출력을 생성할 수 있는 "Fuzzy Chip"인 AL220을 판매한다. 칩의 블록 다이어그램은 다음과 같다.

              +---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- ^                    V +----------------------------++++++++++++++++++++++++++++++++++++++++++++++++++                                                                                 8 +-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++                                                                          +------++++ 파라미터 메모리 256 x 8 +-------------------------+ ADC: 아날로그-디지털 변환기 DAC: 디지털-아날로그 변환기 SH:   견본/보유 

안티록 브레이크

예를 들어 마이크로컨트롤러 칩에 의해 제어되는 ABS를 고려하십시오. 마이크로컨트롤러는 시스템의 브레이크 온도, 속도 및 기타 변수에 기초하여 결정을 내려야 한다.

이 시스템의 변수 "온도"는 "상태"의 범위, 즉 "콜드", "쿨", "모더레이트", "따뜻함", "핫", "매우 뜨거움"으로 세분될 수 있다. 한 상태에서 다음 상태로의 전환은 정의하기 어렵다.

임의의 정적 임계값은 "warm"을 "hot"에서 "warm"으로 나누도록 설정할 수 있다. 예를 들어, 정확히 90도에서, 따뜻한 끝과 뜨거운 것이 시작된다. 그러나 이것은 입력 값이 그 임계값을 통과할 때 불연속적인 변화를 초래할 것이다. 제동 상황에서 요구되는 것처럼 전환이 순탄하지 않을 것이다.

이것을 둘러싼 방법은 그 주들을 흐릿하게 만드는 것이다. 즉, 한 상태에서 다음 상태로 점진적으로 변화하도록 허용한다. 그러기 위해서는 서로 다른 요소들 사이에 동적 관계가 성립되어야 한다.

먼저 "멤버십 함수"를 사용하여 입력 온도 상태를 정의하십시오.

이 방법으로 입력 변수의 상태는 더 이상 한 상태에서 다음 상태로 갑자기 점프하지 않는다. 대신 온도가 변하면 한 멤버십 함수에서 가치를 잃고 다음 멤버십 함수에서는 가치를 얻는다. 즉, 온열기 카테고리에서 순위가 높아질수록 냉기 카테고리의 순위는 낮아진다.

어떤 샘플링된 시간 프레임에서, 브레이크 온도의 "진실 값"은 거의 항상 '0.6 공칭 및 0.4 warm' 또는 '0.7 공칭 및 0.3 cool' 등의 두 가지 멤버쉽 기능의 일부분일 것이다.

위의 예는 복수의 값에서 값 추상화를 이용한 단순한 응용을 보여준다. 그러나 이 경우 온도는 한 가지 종류의 데이터만 나타낸다.

설계한 퍼지 시스템에 따라 동적 기능에서 설정된 트랙션, 속도, 관성과 같은 추가 요인에 의해 이 제동 시스템에 추가적인 정교함을 추가할 수 있다.^[10]

퍼지 제어의 논리적 해석

외관상에도 불구하고 IF-TEN 규칙에 대한 엄격한 논리적 해석을 내리는 데는 몇 가지 어려움이 있다. 예를 들어, 첫 번째 순서 공식 Cold(x)→High(y)에 의해 IF(온도는 "콜드") THEN(히터는 "하이")로 해석하고 r이 Cold(r)가 거짓인 입력이라고 가정한다. 그런 다음 콜드(r)→하이(t) 공식은 t에 대해 참이며, 따라서 t는 r이 주어진 정확한 제어를 제공한다. 퍼지 조절에 대한 엄격한 논리적 정당성은 퍼지 조절이 하젝의 기본 논리 이론으로 표현되는 하젝의 책(7장 참조)에 제시되어 있다.^[2]

2005년 Gerla에서는 퍼지 제어에 대한 또 다른 논리적 접근방식이 퍼지 논리 프로그래밍에 기초하여 제안된다. IF-DEN 시스템 규칙에서 발생하는 퍼지 함수를 f로 나타낸다. 그런 다음 이 시스템은 "좋은(x,y)"인 일련의 규칙을 포함하는 퍼지 프로그램 P로 번역될 수 있다. 가장 모호하지 않은 P의 Herbrand 모델에서 이 술어의 해석은 f와 일치한다. 이것은 퍼지 조절에 더 유용한 도구를 제공한다.

퍼지 질적 시뮬레이션

인공지능 시스템이 액션 시퀀스를 계획할 수 있게 되기 전에, 어떤 종류의 모델이 필요하다. 비디오 게임의 경우, 모델은 게임 규칙과 동일하다. 프로그래밍의 관점에서, 게임 규칙은 플레이어로부터 액션을 받아들이고 액션이 유효한지 계산하는 물리 엔진으로 구현된다. 액션이 실행된 후 게임은 후속 조치 상태에 있다. 만약 그 목적이 수학적인 게임만 하는 것이 아니라 실제 세계의 어플리케이션에 대한 동작을 결정하는 것이라면, 가장 분명한 병목현상은 게임 규칙이 없다는 것이다. 첫 번째 단계는 도메인을 모델링하는 것이다. 시스템 식별은 정확한 수학 방정식이나 퍼지 규칙으로 실현할 수 있다.^[12]

도메인의 전진 모델을 만들기 위해 퍼지 논리와 ANFIS 시스템(어댑티브 네트워크 기반 퍼지 추론 시스템)을 사용하는 것은 많은 단점이 있다.^[13] 정성 시뮬레이션은 정확한 추적 상태를 확인할 수 없지만, 시스템은 조치가 취해진 경우 어떤 일이 일어날지 추측할 뿐이다. 퍼지 질적 시뮬레이션은 정확한 수치 값을 예측할 수 없지만, 미래에 대해 추측하기 위해 부정확한 자연 언어를 사용하고 있다. 그것은 현재 상황과 과거의 행동을 더하고 게임의 예상 후속 상태를 생성한다.

ANFIS 시스템의 출력은 정확한 정보를 제공하지 않고, 예를 들어 [0,0.2,0.4,0]과 같은 퍼지 집합 표기법만 제공하고 있다. 설정된 표기법을 다시 숫자로 변환한 후에는 정확도가 나빠진다. 이것은 퍼지 질적 시뮬레이션을 실제 적용에 좋지 않은 선택으로 만든다.^[14]

적용들

퍼지 제어 시스템은 불확실성 및 비선형 거동을 포함하여 공정 복잡성이 높을 때 적합하며, 사용할 수 있는 정밀한 수학적 모델이 없을 때 적합하다. 퍼지 제어 시스템의 성공적인 적용은 80년대부터 선구적인 해결책을 가지고 일본을 중심으로 전 세계적으로 보고되어 왔다.

문헌에 보고된 일부 신청서는 다음과 같다.

• 에어컨^[15]
• 카메라의^[16] 자동 초점 시스템
• 가전제품(냉장고, 세탁기...)^[17]
• 산업 프로세스 및 시스템의^{[18][19][20][21][22]} 제어 및 최적화
• 글쓰기 시스템^[23]
• 엔진의^[24] 연료 효율
• 환경^[25]
• 전문가 시스템^[26]
• 의사결정 나무^[27]
• 로보틱스^[28][29]
• 자율주행차^[30][31][32]

참고 항목

• 동적 논리학
• 베이시안 추론
• 함수 근사
• 퍼지 개념
• 퍼지 마크업 언어
• 히스테레시스
• 신경망
• 신경 퍼지
• 퍼지 제어 언어
• 유형 2 퍼지 세트 및 시스템

참조

추가 읽기

• 케빈 M. 패시노와 스티븐 유코비치, 퍼지 컨트롤, 애디슨 웨슬리 롱먼, 멘로 파크, 1998년(522쪽)
• Kazuo Tanaka; Hua O. Wang (2001). Fuzzy control systems design and analysis: a linear matrix inequality approach. John Wiley and Sons. ISBN 978-0-471-32324-2.
• 콕스, E. (1992년 10월) 퍼지 펀더멘털. IEEE 스펙트럼, 29:10. 페이지 58–61.
• Cox, E. (1993년 2월) 적응 퍼지 시스템. IEEE 스펙트럼, 30:2. 페이지 7–31.
• 얀 얀젠 덴마크 공과대학 "Fuzzy PID Controllers의 튜닝"은 1998년 9월 30일 98-H 871을 보고한다. [1]
• 퍼지 조절의 기초가 되는 얀 얀젠. Wiley, 2007(209페이지) (목록)
• 컴퓨터 인텔리전스: Kruse, Borgelt, Klawonn, Moewes, Steinbrecher, Hold, 2013, Springer, ISBN 9781447150121의 방법론적 소개

외부 링크

• 퍼지 제어 소개
• 임베디드 마이크로컴퓨터 및 제어시스템의 퍼지 논리
• IEC 1131-7 CD1 IEC 1131-7 CD1 PDF
• 3가지 퍼지 규칙이 있는 시스템의 온라인 대화형 데모
• 데이터 기반 퍼지 시스템