역진자

1976년 경의 단순한 로봇 시스템인 밸런스 카트.카트에는 로드의 각도를 모니터링하고 카트를 앞뒤로 움직여 똑바로 유지하는 서보 시스템이 포함되어 있습니다.

역진자는 그 중심점 위에 질량의 중심이 있는 진자이다.그것은 불안정해서 추가적인 도움이 없으면 넘어질 것이다.폴의 각도를 감시하는 제어장치를 사용하여 폴이 넘어지기 시작할 때 피벗 지점을 질량 중심 아래로 수평으로 이동시켜 균형을 유지함으로써 이 반전 위치에 안정적으로 매달 수 있다.역진자는 역학 및 제어 이론의 고전적인 문제이며 제어 전략을 테스트하기 위한 벤치마크로 사용된다.사진과 같이 전자 서보 시스템의 제어 하에 수평으로 이동할 수 있는 카트에 장착된 피벗 포인트로 구현되는 경우가 많습니다. 이를 카트 및 폴 ^[1]장치라고 합니다.대부분의 애플리케이션은 극을 회전 축에 고정함으로써 진자를 1 자유도로 제한합니다.정상적인 진자가 아래로 매달려 있을 때, 역진자는 본질적으로 불안정하며, 직립을 유지하기 위해 능동적으로 균형을 잡아야 한다; 이것은 피드백 시스템의 일부로 피벗 포인트를 수평으로 이동함으로써, t에 장착된 질량의 회전 속도를 변경함으로써 피벗 포인트에서 토크를 적용함으로써 이루어질 수 있다.피벗 축과 평행한 축에 진자를 두어 진자에 순 토크를 발생시키거나 피벗 지점을 수직으로 진동시킨다.피드백 시스템에서 피벗 포인트를 이동하는 간단한 시연은 뒤집힌 빗자루를 손가락 끝에 놓고 균형을 잡는 것으로 이루어진다.

두 번째 유형의 역진자는 높은 구조물의 틸트미터로, 기초의 하단에 고정되고 플로트의 중립 위치의 움직임을 측정하기 위한 장치를 가진 구조물 상부의 오일 풀 내의 플로트에 부착된 와이어로 구성되어 있다.

개요

지지대 피벗 바로 아래에 보브가 매달려 있는 진자는 안정적인 평형 지점에 있습니다. 진자에 토크가 없으므로 진자는 움직이지 않고, 이 위치에서 벗어나면 평형 위치로 되돌아가는 복원 토크가 발생합니다.안정된 평형 위치에서 180° 떨어진 피벗 바로 위의 강체 막대에 지지된 반전 위치에 있는 보브의 진자는 불안정한 평형 지점에 있다.이 시점에서도 진자에 토크는 없지만, 이 위치에서 조금만 벗어나도 진자에 중력 토크가 발생하여 진자가 평형에서 멀어지게 되고, 진자는 넘어지게 됩니다.

이 반전위치에서 진자를 안정시키기 위해 진자의 각도를 감시하고 진자가 쓰러지기 시작할 때 피벗점의 위치를 옆으로 이동시켜 균형을 유지하는 피드백 제어시스템을 이용할 수 있다.역진자는 역학 및 제어 이론의 고전적인 문제이며 제어 알고리즘(PID 제어기, 상태 공간 표현, 신경 네트워크, 퍼지 제어, 유전 알고리즘 등)을 테스트하기 위한 벤치마크로 널리 사용된다.이 문제에 대한 변형으로는 여러 링크가 있으며, 진자를 유지하면서 카트의 움직임을 명령할 수 있으며, 시쏘에서 카트-진자 시스템의 균형을 맞출 수 있다.역진자는 로켓 또는 비산물 ^[2]유도와 관련이 있으며, 무게 중심은 공기역학적 불안정성을 유발하는 항력 중심 뒤에 위치한다.유사한 문제에 대한 이해는 단순한 로봇 공학으로 균형 카트 형태로 나타낼 수 있습니다.뒤집힌 빗자루를 손가락 끝에 놓고 균형을 잡는 것은 간단한 시연으로, Segway PT, 셀프 밸런스 호버보드, 셀프 밸런스 외발자전거와 같은 자기 밸런스형 퍼스널 트랜스포터로 문제를 해결한다.

피드백이나 제어 메커니즘 없이 반전 진자를 안정시킬 수 있는 또 다른 방법은 피벗을 빠르게 위아래로 진동시키는 것입니다.이것은 카피자의 추라고 불린다.만약 진동이 충분히 강하다면(가속도와 진폭 측면에서) 역진자는 눈에 띄게 반직관적인 방식으로 섭동으로부터 회복할 수 있다.구동점이 단순한 고조파 운동으로 움직이면 진자의 운동은 마티외 ^[3]방정식으로 설명된다.

운동 방정식

역진자의 운동 방정식은 진자의 움직임에 어떤 제약이 가해지는가에 따라 달라집니다.반전 진자는 다양한 구성으로 생성될 수 있으며, 그 결과 진자의 동작을 설명하는 운동 방정식이 다수 생성됩니다.

고정 피벗점

진자의 피벗점이 공간에 고정된 구성에서 운동방정식은 비반전진자의 운동방정식과 유사하다.아래의 운동 방정식은 마찰이나 이동에 대한 다른 저항, 단단한 무질량 막대 및 2차원 이동에 대한 제한을 가정합니다.

(\displaystyle\ddot\theta}}-{g\over\ell}\sin \theta = 0}

여기서 $({$ })은 ${\ddot {\theta }}$ 진자의 각가속도 $,$ g({ $displaystyle$ g $g$ })는 지구 표면의 표준 중력 $,$ $display({$ displaystyle\ $ell$ 은 $\theta$ 진자의 길이, $display({$ displaystyle\ $theta$ })는 평형 포지션에서 측정한 각변위치다.n.

${\ddot {\theta }}$ 에 ${\ddot {\theta }}$ ${\ddot {\theta }}$ displaystyle ${dddot$ {theta ${\ddot {\theta }}$ }})을 추가하면 각가속도 항과 같은 부호가 나타납니다.

{\displaystyle\ddot\theta}={g\over\ell}\sin\theta}

따라서, 역진자는 처음에 변위된 방향으로 수직의 불안정한 평형에서 벗어나 가속되며, 가속도는 길이에 반비례한다.키가 큰 추는 키가 작은 추보다 천천히 떨어진다.

토크 및 관성 모멘트를 이용한 유도:

카트에 있는 역추의 개략도입니다.막대기는 질량이 없는 것으로 간주됩니다.카트의 질량과 로드 끝의 점 질량은 M과 M으로 표시됩니다.그 막대의 길이는 l이다.

진자는 질량 없는 강성봉의 끝에 부착된 $질량$ m(\ $displaystyle$ m $m$ 의 점 질량과 반대쪽 $\ell$ 의 피벗 지점에 부착된 길이 $θ(\$ displaystyle \ $ell$ 의 점 질량으로 구성된다고 가정한다.

시스템의 순 토크는 관성 모멘트에 각 가속도를 곱한 값과 같아야 합니다.

{\mathrm {net}}=I {\ddot {\theta }

순 토크를 제공하는 중력에 의한 토크:

{\mathrm {net} =mg\ell \sin \theta \,\!

$\theta \$ 서 ${\$ { $displaystyle \theta$ \ $}$ 는 $\theta \$ 반전 평형 위치에서 측정된 각도입니다.

결과 방정식은 다음과 같습니다.

(\displaystyle I {\theta }}=mg\ell \sin \theta \,\!

점 질량에 대한 관성 모멘트:

I=mR^{2}

반전진자의 경우 반지름은 로드의 길이인 $\ell$ ${\displaystyle$ \ $ell$ 입니다.

$I=m\ell ^{2}$ $I=m\ell ^{2}$ $I=m\ell ^{2}$ $I=m\ell ^{2}$ 2 { $displaystyle$ I = $m\ell$ ^{ $2}}$ 대체

m\ell ^{2}{\ddot {\theta }}=mg\ell \sin \theta \,\!

질량과 $\ell ^{2}$ 2 $(\$ })는 $\ell ^{2}$ 양쪽에서 분할되어 다음과 같이 됩니다.

{\displaystyle\ddot\theta}={g\over\ell}\sin\theta}

카트의 역진자

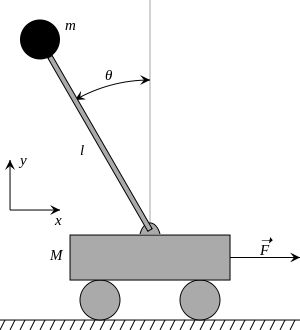
카트상의 반전진자는 인접한 이미지와 같이 수평방향으로 움직이는 베이스에 축지된 $\ell$ 길이 $θ$ 의 극상부에 $질량$ m $(\displaystyle$ m $)$ 으로 $m$ 구성됩니다.카트는 선형 운동으로 제한되며 움직임을 유발하거나 방해하는 힘에 노출됩니다.

안정화의 요점

역진자 안정의 본질은 세 단계로 질적으로 요약할 수 있다.

와인잔이 위에 있는 카트에 사용되는 간단한 안정화 제어 시스템.

1. 틸트 각도 $\theta$ style \ $theta)$ 가 $\theta$ 우측일 경우 카트는 우측으로 가속해야 하며, 그 반대도 마찬가지입니다.

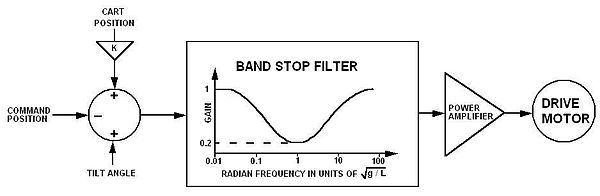
2. 카트 $({display$ x $})$ 의 $x$ 트랙 중심에 대한 위치는 카트 위치별로 늘 각도(제어 시스템이 늘을 시도하는 각도 오류)를 약간 변조하여 안정화됩니다. 즉, k $({displaystyle$ k $})$ 가 작은 $Null$ 각도 $=\theta +kx$ $=\theta +kx$ + $=\theta +kx$ x $=$ \ $theta$ $k$ + $=\theta +kx$ k }입니다.이로 인해 폴이 트랙 중심 쪽으로 약간 기울고 틸트 각도가 정확히 수직인 트랙 중심에서 안정되기를 원합니다.틸트 센서 또는 트랙 기울기에서 그렇지 않으면 불안정성을 야기할 수 있는 오프셋은 안정적인 위치 오프셋으로 변환됩니다.추가 오프셋은 위치 제어를 제공합니다.

(삼) 크레인에 의해 인양되는 하중과 같이 움직이는 피벗점의 대상이 되는 정상적인 진자는 진자 라디안 주파수 $\omega _{p}={\sqrt {g/\ell }}$ p $=$ / $\omega _{p}={\sqrt {g/\ell }}$ {p} ({displaystyle \ $Omega$ _ ${p$ }= $θrt {g/\ell$ 의 피크응답성을 가지며, 제어되지 않는 흔들림을 방지하기 위해 피벗 동작의 주파수 스펙트럼을 $\omega _{p}$ p $근처$ 에서 억제해야 한다. $tyle \opega$ _ ${p$ 입니다.역진자는 안정성을 얻기 위해 동일한 억제 필터가 필요합니다.

Null 각도 변조 전략의 결과로 위치 피드백은 양의 값입니다. 즉, 오른쪽으로 이동하라는 갑작스러운 명령은 진자를 재조정하기 위해 왼쪽으로 초기 카트 모션을 생성한 다음 오른쪽으로 이동하게 됩니다.안정적인 시스템을 만들기 위한 진자 불안정성과 양의 위치 피드백 불안정성의 상호작용은 수학적 분석을 흥미롭고 도전적인 문제로 만드는 특징이다.

라그랑주 방정식으로부터

운동 방정식은 라그랑주 방정식을 사용하여 도출할 수 있다.오른쪽 도면을 참조합니다.여기서 $\theta (t)$ ( $\theta (t)$ t $\theta (t)$ ) { $displaystyle \theta ( t$ )는 $\theta (t)$ 수직방향에 대한 길이 $l$ { $displaystyle$ l $}$ 의 $l$ 진자의 각도이며, 작용력은 중력과 X방향 외력 F입니다.x ( $x(t)$ ) $x(t)$ { $displaystyle$ x $(t)}$ 를 $x(t)$ 카트의 위치로 $x(t)$ 합니다.

시스템의 운동 $에너지$ T {\ $displaystyle$ T $}$ 는 $T$ 다음과 같습니다.

{{displaystyle T=mvfrac {1}{2}}Mv_{1}^2}+{\frac {1}{2}mv_{2}^2}

$v_{1}$ 서 v 1 $({$ 은 $v_{1}$ 카트의 속도, $v_{2}$ ({ $displaystyle v_{2})$ 는 $v_{2}$ 점 $질량$ m({ $displaystyle$ m $m$ 의 속도입니다. $v_{1}$ 1({ $displaystyle$ $v_$ ${$ $1$ }}) 및 $v_{1}$ $\theta$ $v_{2}$ 2 $({displaystyle v_{$ 2 $v_{2}$ }})는 $\theta$ 속도 기록으로 나타낼 수 있습니다 $.$ 포지션의 첫 번째 파생상품으로

v_{1}^{2}=점 {x}^{2

({displaystyle v_{2}^{2}=\left\frac {d}{\rm {d}}{\rm {d}}{\rm {d}}}{\left(x-ell \sin \theta \right)}\rm {d}}{\left(\cos \ta \right})^{{\right})}}}}{{{\}}}}}}}}{{\}}}}}}}}}}}{\right}}}}}}}}}{\right

$(\$ 의 $v_{2}$ $v_{2}$ 단순화하면 다음과 같은 결과가 나옵니다.

v_{2}^{2}=점 {x}^2}-2\ell {\dot {x}}{\cos \theta +\ell ^{2}{\dot {\theta }^{2}{\dot}.

이제 운동 에너지는 다음과 같이 제공됩니다.

T=param frac {1}{2}\left(M+m\right){\dot {x}{\ell {\dot {x}}{\cos \theta +{1}{2}}m\ell ^2}{\dot {\theta}.

$\theta$ 의 일반화 좌표는 ${\(\displaystyle$ \ $theta)$ $x$ x(\ $displaystyle$ x $x$ 이며 각각 일반화 힘을 가집니다. $x축$ 에서 $x$ $Q_{x}$ $Q_{x}$ x{\ $displaystyle Q_{x}$ 는 $Q_x$ 가상 작업을 통해 계산할 수 있습니다.

Q_{x}\delta x=F\delta x,\display Q_{x}=F,

${\$ { $displaystyle \theta }$ $Q_{\theta }$ 에서는 $\theta$ $Q_{\theta }$ Q ${\$ { \ $displaystyle$ Q _ { \ $theta }$ 도 $Q_{\theta }$ 가상 작업을 통해 계산할 수 있습니다.

\displaystyle Q_{\theta }\display \theta = mgl\sin \theta \display Q_{\theta }= mgl\sin \theta .}

라그랑주 방정식에 따르면 운동 방정식은 다음과 같습니다.

{\frac {d} {\mathrm {d} t} {\filen {T} - {\filen {T} \over \filen x} = F,

{\frac {d} {\mathrm {d} t} {\mathrm {d}} {\t} - {\time {T} } = mgl \sin \theta

다음 방정식에서T(\ $displaystyle$ T $)$ 를 $T$ $T$ 하고 단순화를 통해 역진자의 운동을 설명하는 방정식이 도출됩니다.

\displaystyle \left(M+m\오른쪽) {\ddot {x}-mell {ddot {theta }\cos \theta +m\ell {dot \theta } {{2}\sin \theta = F,}

(\displaystyle\ell\dddot\theta\g\sin\theta=cos\theta{x}\cos\theta})

이러한 방정식은 비선형적이지만 제어 시스템의 목적은 진자를 똑바로 세우는 것이므로 방정식은 $\theta \approx 0$ 0 $(\displaystyle \theta \apprough$ 0 $\theta \approx 0$ 주위에 선형화할 수 있습니다.

오일러-라그랑주 방정식으로부터

일반화력은 $V_{x}$ 에너지 $V_{x}$ x ${\$ V_{ $x}}$ 및 $V_{x}$ $V_{\theta }$ ${\$ {\ $displaystyle V_{\theta$ $V_{\theta }$ 로 표기할 수 있습니다.

일반화된 힘	잠재 에너지
$Q_{x}=F$	$V_{x}=\int _{t_{0}}^{t}F{\dot {x}}\{rm {d}}t$
$\displaystyle Q_{\theta }= mgl\sin \theta }$	$\displaystyle V_{\theta }= mgl\cos \theta }$

달랑베르의 원리에 따르면 일반화된 힘과 위치 에너지는 연결되어 있습니다.

Q_{j}=partial frac {\mathrm {d} t}}{\frac {\partial V}{\frac {q}_{j}}-{\frac {\partial q_{j},},

그러나 특정 상황에서는 잠재적 에너지에 접근할 수 없으며 일반화된 힘만 사용할 수 있습니다.

${\mathcal {L}}=T-V$ L $=$ - ${\mathcal {L}}=T-V$ (\ $displaystyle$ {\ $mathcal {$ L}}= $T-V$ 를 구한 후, 오일러-라그랑지 방정식을 사용하여 운동 방정식을 풀 수도 있습니다.

{\frac {\partial {\mathcal {L}}}{\partial x}}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}}}\right)=0

L

{\frac {\partial {\mathcal {L}}}{\partial x}}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}}}\right)=0

{\frac {\partial {\mathcal {L}}}{\partial x}}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}}}\right)=0

-

{\frac {\partial {\mathcal {L}}}{\partial x}}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}}}\right)=0

（

{\frac {\partial {\mathcal {L}}}{\partial x}}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}}}\right)=0

{\frac {\partial {\mathcal {L}}}{\partial x}}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}}}\right)=0

{\frac {\partial {\mathcal {L}}}{\partial x}}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}}}\right)=0

=

0

{

displaystyle

{

frac { mathcal

{ L } { \

partial x

} - { \

frac { d

} { \

mathrm

{ d } { d } { \

frac

} { \

frac

\

mathcal

} { d t

}

{ light

}

{\frac {\partial {\mathcal {L}}}{\partial \theta }}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {\theta }}}}\right)=0

-

{\frac {\partial {\mathcal {L}}}{\partial \theta }}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {\theta }}}}\right)=0

t (

{\frac {\partial {\mathcal {L}}}{\partial \theta }}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {\theta }}}}\right)=0

-

{\frac {\partial {\mathcal {L}}}{\partial \theta }}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {\theta }}}}\right)=0

{\frac {\partial {\mathcal {L}}}{\partial \theta }}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {\theta }}}}\right)=0

)

=

0 ( \

style

\

frac { mathcal

{ L

{\frac {\partial {\mathcal {L}}}{\partial \theta }}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {\theta }}}}\right)=0

) { \

fartial

\

theta

} - { \ frac { d } { \

mathrm

{

d }

{ \

frac

\

frac

{ d } \

frac

{ d } { \

dotal }

유일한 차이점은 일반화된 힘을 잠재적 $V_{j}$ V $j$ 에 $V_{j}$ 통합할지 또는 오른쪽에 $Q_{j}$ 로 $Q_{j}$ $Q_{j}$ 으로 쓸지 여부입니다. 이러한 힘은 모두 최종에서 동일한 방정식으로 이어집니다.

뉴턴의 제2법칙에서

종종 라그랑주 방정식 대신 뉴턴의 제2법칙을 사용하는 것이 유리하다. 왜냐하면 뉴턴의 방정식은 추와 수레 사이의 접합부에서 반작용력을 주기 때문이다.이러한 방정식은 각 본체에 대해 x방향과 y방향의 두 가지 방정식을 생성합니다.카트의 운동 방정식은 아래에 나와 있습니다. 여기서 LHS는 차체에 가해지는 힘의 합이고 RHS는 가속도입니다.

F-R_{x}=M{\ddot {x}

F_{N}-R_{y}-Mg=0

$R_{x}$ 의 $R_{x}$ 에서 R $R_{x}$ x {\ $displaystyle R_{x}$ $R_{y}$ $R_{y}$ y {\ $displaystyle R_{y}$ 는 $R_{y}$ 접합부의 반력입니다. $(\$ 은 $F_{N}$ 카트에 가해지는 일반적인 힘입니다.이 두 번째 방정식은 수직 반력에만 의존하므로 방정식을 사용하여 정규 힘을 풀 수 있습니다.첫 번째 방정식은 수평 반력을 푸는 데 사용할 수 있다.운동방정식을 완성하기 위해서는 진자에 부착된 점질량의 가속도를 계산해야 한다.점 질량의 위치는 다음과 같이 관성 좌표에서 지정될 수 있다.

{r}_{P}=(x-\ell \sin \theta){\hat {x}_{I+\ell \cos \theta \hat {y}_{I}

두 개의 도함수를 취하면 관성 기준 프레임에서 가속도 벡터가 생성됩니다.

(*displaystyle {vec {a}_{P/I}=ddot {x}+\ell\theta -\cos \theta}{cos \theta}+(\ell\the tell)I}}

그런 다음 뉴턴의 제2법칙을 사용하여 x방향과 y방향으로 두 개의 방정식을 작성할 수 있습니다.반력은 진자에 가하면 양이고 카트에 가하면 음이다.이것은 뉴턴의 제3법칙 때문이다.

({displaystyle R_{x}=m({\ddot {x}}+\ell {dot {theta }^{2}\sin \theta -\ell {ddta }\cos \theta})

({displaystyle R_{y}-mg=m(-ell {{theta}}^{2}\cos \theta -\ell {dddot {theta}}}\sin \theta)}

첫 번째 방정식은 가해진 $힘$ F $(\displaystyle$ F $)$ 를 $F$ 모르는 경우 수평 반력을 계산하는 또 다른 방법을 허용합니다.두 번째 방정식은 수직 반력을 푸는 데 사용할 수 있습니다.첫 번째 운동방정식은 $F-R_{x}=M{\ddot {x}}$ F - $F-R_{x}=M{\ddot {x}}$ $R_{x}=m({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta )$ $=$ $F-R_{x}=M{\ddot {x}}$ x ${\$ { \ $displaystyle$ F - R _ { x } = M { \ $ddot$ { x $R_{x}=m({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta )$ } $R_{x}=m({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta )$ $R_{x}=m({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta )$ m ( $R_{x}=m({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta )$ x + $R_{x}=m({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta )$ 2 sin $R_{x}=m({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta )$ - ⁡ - $R_{x}=m({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta )$ $R_{x}=m({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta )$ ⁡ $=$ { $displaystyle$ R _ $dd$ { $x$ } )로 $F-R_{x}=M{\ddot {x}}$ 하여 도출된다.

\displaystyle \left(M+m\right) {x}-mell {ddot {theta }\cos \theta +m\ell {dot \theta }{2}\sin \theta = F}

검사 결과 이 방정식은 라그랑주 방법의 결과와 동일하다.두 번째 방정식을 얻기 위해 진자 운동 방정식은 항상 진자에 수직인 단위 벡터로 점철되어야 하며 일반적으로 본체 프레임의 x 좌표로 기록되어야 한다.관성 좌표에서 이 벡터는 단순한 2-D 좌표 변환을 사용하여 기록될 수 있습니다.

\displaystyle\hat {x}_{B}=\cos\theta\hat {x}_{I+\sin \theta \hat {y}_{I}}

벡터 형태로 쓰인 진자 운동 방정식은 $\sum {\vec {F}}=m{\vec {a}}_{P/I}$ of $\sum {\vec {F}}=m{\vec {a}}_{P/I}$ $\sum {\vec {F}}=m{\vec {a}}_{P/I}$ $\sum {\vec {F}}=m{\vec {a}}_{P/I}$ $\sum {\vec {F}}=m{\vec {a}}_{P/I}$ $\sum {\vec {F}}=m{\vec {a}}_{P/I}$ / $\sum {\vec {F}}=m{\vec {a}}_{P/I}$ { $displaystyle \sum {F}$ = $m$ {\ $vec$ { $a$ $}}_{P/I$ 이다. ${\hat {x}}_{B}$ x ^ ${\hat {x}}_{B}$ ^ B { $displaystyle {x}$ _ ${$ B}는 LHS 전치 a와 같다.

{\displaystyle({\hat {x}}_{B})^{T}\sum {VEC {F}}=hat {x}_{B}^{T}(R_{x}{\hat {x}}_{I}+R_{y}{\hat {y}_{I}-mg{y}=mg\hat {x}_{B}^T}(R_{p}{\hat {y}_{B}-mg{\hat {y}_{I}=mg\sinta})

상기 등식에서는 반력의 차체 프레임 성분과 반력의 관성 프레임 성분과의 관계를 이용한다.점 질량을 카트에 연결하는 막대가 무질량이라는 가정은 이 막대가 막대에 수직인 하중을 전송할 수 없음을 의미합니다.따라서 반력의 관성 프레임 성분은 간단히 $R_{p}{\hat {y}}_{B}$ p $R_{p}{\hat {y}}_{B}$ ^ $R_{p}{\hat {y}}_{B}$ ${\$ 로 $R_{p}{\hat {y}}_{B}$ 표기할 수 있으며, 이는 막대가 막대 자체의 축을 따라서만 하중을 전달할 수 있음을 의미한다.이로 인해 로드 자체의 장력을 푸는 데 사용할 수 있는 또 다른 방정식이 생성됩니다.

R_{p}=sqrt {R_{x}^2}+R_{y}^2}}

방정식의 RHS는 진자의 가속도와 함께 x ${\hat {x}}_{B}$ ^ $(\$ 에 ${\hat {x}}_{B}$ ${\hat {x}}_{B}$ 을 찍어 유사하게 계산한다.그 결과(일부 간략화 후)는 다음과 같습니다.

{\displaystyle mbat {x}_{B}^T}({\vec {a}}_{P/I})=m({\ddot {x}})\cos \theta -\ell {ddot {theta }}})

LHS와 RHS를 결합하여 m의 수율로 나눈다.

{\displaystyle\ell\dddot\theta}-g\sin\theta=cos\theta}

라그랑주 방법의 결과와 똑같아요뉴턴의 방법을 사용하면 모든 반작용력이 드러나 아무것도 손상되지 않는다는 장점이 있다.

변종

역진자의 안정성을 달성하는 것은 ^[4]연구자들에게 공통된 엔지니어링 과제가 되었다.카트의 역진자에는 카트의 로드부터 카트의 다중 세그먼트 역진자까지 다양한 변형이 있습니다.또 다른 변형은 반전 진자의 로드 또는 세그먼트화된 로드를 회전 어셈블리의 끝에 배치합니다.둘 다 (카트와 회전 시스템) 역진자는 평면 내에서만 떨어질 수 있습니다.이러한 프로젝트의 역진자는 평형 위치가 달성된 후에만 균형을 유지하도록 요구되거나 스스로 평형을 달성할 수 있다.또 다른 플랫폼은 이륜 균형 역진자입니다.바퀴가 2개인 플랫폼은 그 자리에서 회전할 수 있는 기능을 갖추고 있어 조작성이 ^[5]뛰어납니다.그러나 또 다른 변동은 단일 포인트에서 균형을 잡습니다.회전하는 팽이, 외발자전거, 또는 구형의 공 위에 있는 역추는 모두 한 점에서 균형을 잡습니다.

카피차 진자의 구성 방법을 나타내는 그림: 모터가 크랭크를 고속으로 회전시키고, 크랭크가 레버 암을 상하로 진동시켜 진자가 피벗으로 부착됩니다.

카피자의 추

피벗이 빠르게 상하로 요동하는 역진자는 역위치로 안정될 수 있다.이것을 처음 분석한 러시아 물리학자 표트르 카피자의 이름을 따서 카피자의 추라고 불립니다.질량이 없는 진동 베이스에 연결된 진자의 운동 방정식은 카트의 진자와 같은 방식으로 도출됩니다.이제 점 질량의 위치는 다음과 같이 지정됩니다.

(\displaystyle\leftswell\sin\theta,y+\ell\cos\theta\right)

그리고 그 위치의 첫 번째 도함수를 취함으로써 속도를 구한다.

v^{2}={y}-2\ell {\dot {y}}{\dot {\theta }}\sin \theta +\ell ^{2}{\dot {\theta }}^{2}.

진동 베이스의 반전 진자에 대한 플롯.첫 번째 그림은 느린 진동에 대한 진자의 반응을 보여주고, 두 번째 그림은 빠른 진동에 대한 반응을 보여줍니다.

이 시스템의 Lagrangian은 다음과 같이 쓸 수 있습니다.

({displaystyle L=lft frac {1}{2}}m\left frac {y}^2}-2\ell {dot {y}}{\dot {theta}}\sin \theta +\ell ^{2}{right})-mg(y+ell \cos \ta \right)

운동 방정식은 다음과 같습니다.

\displaystyle \mathrm {d} \over \mathrm {d} \over \mathrm {d} \mathrm {d} \over \mathrm {D} \over \dot \theta } = 0

결과:

{\displaystyle\ell {dtheta}-{\dot {y}}\sin \theta = g\sin \theta }

y가 단순한 고조파 $y=A\sin \omega t$ 인 y $y=A\sin \omega t$ $y=A\sin \omega t$ sin $y=A\sin \omega t$ $y=A\sin \omega t$ { $displaystyle$ y $=A\sin \mega$ t $y=A\sin \omega t$ 을 나타내는 경우, 다음 미분 방정식은 다음과 같습니다.

({displaystyle {ddot {theta }}-{g \over \ell }\sin \theta =-{A \over \ell }\Omega ^{2}\sin \sin \theta } )

이 방정식은 기본적인 폐쇄형 해법을 가지고 있지 않지만 다양한 방법으로 탐구할 수 있다.예를 들어 진동 진폭이 작을 때 마티외 방정식에 의해 밀접하게 근사됩니다.분석에 따르면 진자는 빠른 진동을 위해 직립 상태를 유지한다.첫 번째 그림은 $y$ 가 $y$ 느린 진동일 $때$ 직립 위치에서 방해받으면 진자가 빠르게 넘어지는 것을 보여줍니다.잠시 후 각도 $\theta$ (\ $displaystyle \theta)$ 가 $\theta$ 90°를 초과하여 진자가 땅에 떨어졌습니다.y ${\displaystyle$ y $y$ }가 빠른 진동일 경우 진자를 수직 위치에서 안정적으로 유지할 수 있습니다.두 번째 그림은 수직 위치에서 방해를 받으면 $\theta =0$ 진자가 수직 위치(θ = 0 \ $displaystyle \theta = 0$ )를 중심으로 진동을 시작한다는 것을 보여줍니다.수직 위치로부터의 편차는 작게 유지되어 추가 넘어지지 않습니다.

예

거의 틀림없이 안정화된 역진자의 가장 일반적인 예는 인간이다.똑바로 서 있는 사람은 발을 축으로 하여 역추 역할을 하며, 지속적인 작은 근육 조절이 없으면 넘어질 수 있습니다.인간의 신경계는 무의식적인 피드백 제어 시스템, 눈, 근육, 관절로부터의 고유 수용성 입력과 내이에 있는 세 개의 반고리관과 두 개의 이석 기관으로 구성된 전정계로부터의 방향 입력을 사용하여 지속적으로 작은 조절을 만드는 균형 감각 또는 올바른 반사를 포함합니다.골격근육에 힘을 주어 똑바로 서게 하는 겁니다걷거나 뛰거나 한 발로 균형을 잡는 것은 이 시스템에 추가적인 부담을 줍니다.특정 질병과 알코올 또는 약물 중독은 이러한 반사를 방해하여 어지럼증과 불감증, 똑바로 설 수 없는 상태를 야기할 수 있습니다.경찰이 음주나 약물의 영향을 운전자들에게 테스트하기 위해 사용하는 현장 음주 테스트는 이러한 반사작용의 손상을 테스트합니다.

간단한 예로는 손으로 빗자루나 미터 스틱의 균형을 잡는 것을 들 수 있습니다.

역진자는 다양한 장치에 사용되어 왔고 역진자의 균형을 맞추려고 시도하는 것은 ^[6]연구자들에게 독특한 공학적인 문제를 야기한다.역진자는 고유의 불안정성으로 인해 모든 ^[7]장애에 대한 측정 가능한 반응을 초래하기 때문에 여러 초기 지진계 설계의 중심 요소였다.

역진자 모델은 이륜 자가 균형 스쿠터나 단륜 전기 외발자전거와 같은 최근의 개인 운송수단에 사용되고 있다.이러한 장치는 운동학적으로 불안정하며 전자 피드백 서보 시스템을 사용하여 직립 상태를 유지합니다.

카트의 진자를 역진자 상태로 흔드는 것은 전통적인 최적 제어 완구 문제/벤치마크로 ^[8]^[9]간주된다.

힘의 제곱을 최소화하는 고정 시간 카트폴 스윙 업의 궤적

「」를 참조해 주세요.

레퍼런스

^ C.A. 해밀턴 유니언 칼리지 시니어 프로젝트
^ "Model Rocket Stability".
^ http://www2.math.ou.edu/~npetrov/petrov-report.pdf^{[베어 URL PDF]}
^ http://robotics.ee.uwa.edu.au/theses/2003-Balance-Ooi.pdf^{[베어 URL PDF]}
^ "Archived copy" (PDF). Archived from the original (PDF) on 2016-03-04. Retrieved 2012-05-01.{{cite web}}: CS1 maint: 제목으로 아카이브된 복사(링크)
^ "Archived copy" (PDF). Archived from the original (PDF) on 2016-03-04. Retrieved 2012-05-01.{{cite web}}: CS1 maint: 제목으로 아카이브된 복사(링크)
^ "The Early History of Seismometry (to 1900)". Archived from the original on 2009-11-28.
^ "The Acrobot and Cart-Pole" (PDF).
^ "Cart-Pole Swing-Up". www.cs.huji.ac.il. Retrieved 2019-08-19.

D. 시스템 및 제어에서의 Liberzon 스위칭(2003 Springer) 페이지 89ff

추가 정보

프랭클린 등(2005).동적 시스템의 피드백 제어, 5, 프렌티스 홀.ISBN 0-13-149930-0

외부 링크

[1] C.A. 해밀턴 유니언 칼리지 시니어 프로젝트

[2] "Model Rocket Stability".

[3] ttp://www2.math.ou.edu/~npetrov/petrov-report.pdf^{[베어 URL PDF]}

[4] ttp://robotics.ee.uwa.edu.au/theses/2003-Balance-Ooi.pdf^{[베어 URL PDF]}

[5] "Archived copy" (PDF). Archived from the original (PDF) on 2016-03-04. Retrieved 2012-05-01.{{cite web}}: CS1 maint: 제목으로 아카이브된 복사(링크)

[6] "Archived copy" (PDF). Archived from the original (PDF) on 2016-03-04. Retrieved 2012-05-01.{{cite web}}: CS1 maint: 제목으로 아카이브된 복사(링크)

[7] "The Early History of Seismometry (to 1900)". Archived from the original on 2009-11-28.

[8] "The Acrobot and Cart-Pole" (PDF).

[9] "Cart-Pole Swing-Up". www.cs.huji.ac.il. Retrieved 2019-08-19.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Search

역진자

네임스페이스

더

목차

개요

운동 방정식

고정 피벗점

카트의 역진자

안정화의 요점

라그랑주 방정식으로부터

오일러-라그랑주 방정식으로부터

뉴턴의 제2법칙에서

변종

카피자의 추

예

「」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

Search

역진자

개요

운동 방정식

고정 피벗점

카트의 역진자

안정화의 요점

라그랑주 방정식으로부터

오일러-라그랑주 방정식으로부터

뉴턴의 제2법칙에서

변종

카피자의 추

예

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

「」를 참조해 주세요.