가보르 웨이블렛

가볼레(Gabor wavelet)는 데니스 가보르가 정보이론 응용에서 푸리에 변환의 기초가 되기 위해 구성한 복잡한 기능을 이용하여 발명한 파장이다.그들은 Morlet 웨이브렛과 매우 비슷하다.가보르 필터와도 밀접한 관련이 있다.웨이블렛의 중요한 특성은 시간과 주파수 영역에서 표준 편차의 산물을 최소화한다는 것이다.다른 방법으로 말하면, 이 웨이블렛이 전달하는 정보의 불확실성은 최소화된다.그러나 그들은 비직관적이라는 단점을 가지고 있기 때문에 효율적으로 그 기초를 분해하는 것은 어렵다.그 시작 이후, 이미지 처리에서부터 인간 시각 시스템의 뉴런 분석까지 다양한 어플리케이션이 등장했다.^[1][2]

최소불확도 특성

Gabor wavelet의 동기는 시간과 빈도 영역에서 표준 편차를 최소화하는$$ $기능{\displaystyle }$ f${\displaystyle }$( ${\displaystyle x}$) ${\displaystyle$ f$(x)}$을 찾는 데서 비롯된다.보다 공식적으로 위치 영역의 분산은 다음과 같다.

${\displaystyle (\Delta x)^{2}={\frac {\int _{-\infty }^{\infty }(x-\mu )^{2}f(x)f^{*}(x)\,dx}{\int _{-\infty }^{\infty }f(x)f^{*}(x)\,dx}}}$

여기서 $f{\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$( ${\displaystyle x}$) ${\displaystyle$ f$^{*}(x)}$은 $f{\displaystyle }$ (${\displaystyle x}$) ${\displaystyle f(x)}$의 복잡한 결합이고 $\mu {\displaystyle }$ ${\displaystyle \mu}$은 산술 평균으로, 다음과 같이 정의된다.

${\displaystyle \mu ={\frac {\int _{-\\f^{}^{*(x)\,dx}{\int _{-\inf^{-\f(x)^{-\inf^{-}f(x)^{\inf(x)\,dx}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

파형 번호 영역의 분산:

${\displaystyle (\Delta k)^{2}={\frac {\int _{-\infty }^{\infty }(k-k_{0})^{2}F(k)F^{*}(k)\,dk}{\int _{-\infty }^{\infty }F(k)F^{*}(k)\,dk}}}$

여기서 $k{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$는 $f{\displaystyle }$ ( ${\displaystyle x}$ )${\displaystyle f($${\displaystyle x}$$)}$ , F ($$$x{\displaystyle }$)${\displaystyle F(x)}$의 푸리에 변환의 산술 평균이다$.$

${\displaystyle k_{0}={\frac {\int _{-\int _{-\inflt }^{\inflt }kF(k)F^{*}(k)\,dk}{\int _{-\infit }^{\f(k)^{*(k)\,dk}}}}}$

이러한 정의에 따라 불확실성은 다음과 같이 기록된다.

${\displaystyle(\Delta x)(\Delta k)}$

이 수량은 하한이 $1{\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \frac{2}{}}$ ${\$}}인 것으로 나타났다$.$양자역학 견해는${\displaystyle }$(${\displaystyle \mathrm{\Delta }}$ ${\displaystyle x}$) ${\displaystyle (\Delta$ $x$$)}$을 위치의 불확실성으로$$ 해석하고 $\Delta {\displaystyle k}$) ${\displaystyle \hbar (\Delta$ k$)}$을 모멘텀의 불확실성으로$$ 해석하는 것이다.이론적으로 가능한 가장 낮은 불확실성 한계를 갖는 함수$$ $f{\displaystyle }$( ${\displaystyle x}$) ${\displaystyle f(x)}$는 가보르 웨이브렛이다.^[3]

방정식

1-D 가보르 파장의 방정식은 복잡한 지수화에 의해 변조된 가우스식이며, 다음과 같이 설명된다.^[3]

${\displaystyle f(x)=e^{-(x-x_{0})^{2}/a^{2}}e^{-ik_{0}(x-x_{0})}}}}}}$

${\displaystyle \sin }$ ${\displaystyle \sin },$ ${\displaystyle \mathrm{cos<img\; alt="\backslash sin\; "\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/ee55beec18afd710e7ab767964b915b020c65093"\; style="vertical-align:\; -0.338ex;\; width:2.856ex;\; height:2.176ex;"\; papago-attr-id="53">}}$ ${\displaystyle \cos }$과 같이 푸리에 변환의 베이스로 일반적으로 사용되는 다른 기능과 달리$,$ 가보르 웨이블렛은 중심 $x{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}${\$displaystyle x_{0}$로부터의 거리가 증가하면$$ 함수의 값이 기하급수적으로 억제된다는 것을 의미한다.${\displaystyle a}$ ${\displaystyle a}$은(는) 이 지수 하강 속도를 제어하고$$ $k{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$은(는) 변조 속도를 제어한다$$.

또한 가보르 웨이블렛의 푸리에 변환도 주목할 필요가 있는데, 가보르 웨이블렛은 다음과 같다.

${\displaystyle F(k)=e^{-(k-k_{0}}^{2}a^{2}}e^{-ix_{0}(k-k_{0})}}}}}}}$

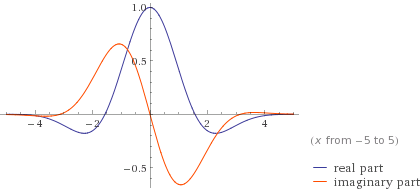
여기에 예시된 웨이블렛이 있다.

개선된 가보르 웨이블렛

이 절의 사실적 정확성은 논쟁의 여지가 있다. 관련 토론은 Talk:Gabor wavelet에서 찾을 수 있다. 논란의 소지가 있는 문구를 안정적으로 소싱할 수 있도록 도와주십시오. (2022년 2월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

^[4] 변형이 불가능한 개선된 가보르 웨이블렛 변형을 제안한다.주파수 $\tau {\displaystyle }$ ${\displaystyle \tau$$}$을(를) 사용하여 $신호{\displaystyle }$ h${\displaystyle (}$ ${\displaystyle ))}$${\$$displaystyle$ $h$$(\tau )$의 개선된 $g${\$displaystyle$ h(\tau )를$$ 사용하는 $스펙트럼{\displaystyle }$ $J$)은 τ {\displaystyparmeau}로 정의된다$$.

${\displaystyle J(f,\tau )=h(\tau )*g_{f,0}(\tau )}$

신호는 다음을 사용하여 재구성할 수 있다.

${\displaystyle h(\tau )=\int _{-\infit }^{\j(f,t)*\exp(j2\pi ft)\,df}$

$\ast {\displaystyle }$ ${\displaystyle *}$은(는) Convolution을 가리킨다는$$ 점에 유의하십시오.웨이블렛은 다음과 같이 정의된다.

${\displaystyle g_{f,\tau }(t)=f g(f\cdot(t-\tau ))}$

${\displaystyle g(t)={\frac {1}{\pi1}{\\sqrt{2*\pi }}}}\expect{\frac{t^{2}}:}+j2\pi t)}}}$

참고 항목

• 가보르 변환
• 가보르 필터
• 모렛 웨이블렛

참조

외부 링크

• 2D Gabor 파장 및 Gabor 기능 추출을 위한 MATLAB 코드