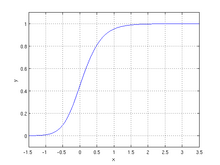
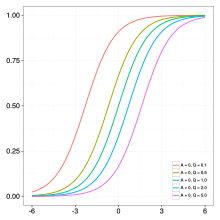
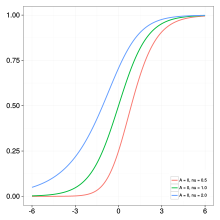
A=0, K=1, B=3, Q=162=0.5, M=0, C=1 다양한 변수 A의 영향. 다른 파라미터는 모두 1이다. 변수 B의 변화 효과. A = 0, 다른 모든 파라미터는 1이다. 다양한 파라미터 C의 영향. A = 0, 다른 모든 파라미터는 1이다. 다양한 파라미터 K의 영향. A = 0, 다른 모든 파라미터는 1이다. 다양한 파라미터 Q의 영향 A = 0, 다른 모든 파라미터는 1이다. 다양한 매개 변수 ν {\displaystyle \nu }. 원래 성장 모델링을 위해 개발된 리차드의 곡선이라고 도 하는 일반화된 로지스틱 함수 또는 곡선 은 로지스틱 또는 S자형 함수의 확장이며, 보다 유연한 S자형 곡선이 가능하다.
Y ( t ) = A + K − A ( C + Q e − B t ) 1 / ν {\displaystyle Y(t)=A+{K-A \over(C+Qe^{-Bt})^{1/\nu }} 여기서 Y {\displaystyle Y} t {\displaystyle t}
5가지 매개 변수가 있다.
A {\displaystyle A} K {\displaystyle K} C {\displaystyle C=1} . A 0 {\displaystyle A=0}, 1 {\displaysty C=1 K {\displaysty } 운반 한다 . B {\displaystyle B} ν 0 {\displaystyle \nu >0} Q {\displaystyle Q} Y {\displaystyle Y(0)} C {\displaystyle C} 그렇지 않으면 위쪽 점근은 A A C 1 ν {\ displaystyle A+{K-A \over C^{\,1/\nu}}} 이 방정식은 다음과 같이 기록할 수도 있다.
Y ( t ) = A + K − A ( C + e − B ( t − M ) ) 1 / ν {\displaystyle Y(t)=A+{K-A \over(C+e^{-B(t-M)}^{1/\nu }} 여기서 M {\displaystyle M} 생각 있는 displaystyle 0}( Y 0 A K C 1 ν {\ displaystystyle Y(t_{0)}) =A+{K-A \over (C+1)^{1/\nu }}}
Q {\displaystyle Q} M {\displaystyle M}
Y ( t ) = A + K − A ( C + Q e − B ( t − M ) ) 1 / ν {\displaystyle Y(t)=A+{K-A \over(C+Qe^{-B(t-M)}^{1/\nu }} 이 표현은 시작 시간과 그 시간에 Y의 값 둘 다의 설정을 단순화한다.
이 일반 모델은 1959년 모델 가족을 위해 일반 형식을 제안한 F. J. 리차드 의 이름을 따서 "리차드의 곡선"으로 명명되기도 한다.
시간 M {\displaystyle M} 로지스틱 은 Q ν 1 {\displaystyle Q=\nu =1} .
일반 로지스틱 미분 방정식 일반화된 로지스틱 함수의 특정한 예는 다음과 같다.
Y ( t ) = K ( 1 + Q e − α ν ( t − t 0 ) ) 1 / ν {\displaystyle Y(t)={K \over(1+Qe^{-\alpha \nu(t-t_{0}})^{1/\nu }}}} RDE(Richards의 미분방정식)의 해답은 다음과 같다.
Y ′ ( t ) = α ( 1 − ( Y K ) ν ) Y {\displaystyle Y^{\premy }(t)=\alpha \left(1-\좌측({\frac {Y}{K}\우측)^{\nu }\우측) Y} 초기 상태로
Y ( t 0 ) = Y 0 {\displaystyle Y(t_{0}}= Y_{0}} 어디에
Q = − 1 + ( K Y 0 ) ν {\displaystyle Q=-1+\왼쪽({\frac {K}{ Y_{0}}\오른쪽)^{\nu }} ν > 0과 α > 0을 전제로 한다.
고전적 로지스틱 미분방정식은 equation =1로 위의 방정식의 특별한 경우인 반면, 곰퍼츠 곡선 은 다음과 같은 경우제한치 → 0 displaystyle \nu \rightarrow 0^{+}
α = O ( 1 ν ) {\displaystyle \alpha =O\left({\frac {1}{\nu }}\오른쪽)} 사실, 작은 ν에게는 그렇다.
Y ′ ( t ) = Y r 1 − 생략하다 ( ν ln ( Y K ) ) ν ≈ r Y ln ( Y K ) {\displaystyle Y^{\prime }(t)=Yr{1-\exp \left(\nu \ln \left)({\frac {Y}{K}\right)}{\nu }}}}{\frac {Y}{K}\rim}\right} RDE는 종양학이나 역학과 같은 분야에서 발생하는 많은 성장 현상을 모델링한다.
일반화된 로지스틱 함수의 그라데이션 데이터에서 매개변수를 추정할 때, 주어진 데이터 지점 displaystyle t}( C 1 {\displaystyle C=1} ,
∂ Y ∂ A = 1 − ( 1 + Q e − B ( t − M ) ) − 1 / ν ∂ Y ∂ K = ( 1 + Q e − B ( t − M ) ) − 1 / ν ∂ Y ∂ B = ( K − A ) ( t − M ) Q e − B ( t − M ) ν ( 1 + Q e − B ( t − M ) ) 1 ν + 1 ∂ Y ∂ ν = ( K − A ) ln ( 1 + Q e − B ( t − M ) ) ν 2 ( 1 + Q e − B ( t − M ) ) 1 ν ∂ Y ∂ Q = − ( K − A ) e − B ( t − M ) ν ( 1 + Q e − B ( t − M ) ) 1 ν + 1 ∂ Y ∂ M = − ( K − A ) Q B e − B ( t − M ) ν ( 1 + Q e − B ( t − M ) ) 1 ν + 1 {\displaystyle{\begin{정렬}\\{\frac{Y\partial}{A\partial}}&=1-(1+Qe^{-B(t-M)})^{-1/\nu}\\\\{\frac{Y\partial}{K\partial}}&=(1+Qe^{-B(t-M)})^{-1/\nu}\\\\{\frac{Y\partial}{B\partial}}&={\frac{(K-A)(t-M)Qe^{-B(t-M)}}{\nu(1+Qe^{-B(t-M)})^{{\frac{1}{\nu}}+1}}}\\\\{\frac{Y\partial}{\nu\partial}}&){\frac{(K-A)\ln(1+Q.e^{-B(t-M)})}{\n u ^{2}(1+Qe^{-B(t-M)})^{\frac {1}{\nu }}}}\\\\{\frac {\partial Y}{\partial Q}}&=-{\frac {(K-A)e^{-B(t-M)}}{\nu (1+Qe^{-B(t-M)})^{{\frac {1}{\nu }}+1}}}\\\\{\frac {\partial Y}{\partial M}}&=-{\frac {(K-A)QBe^{-B(t-M)}}{\nu (1+Qe^{-B(t-M)})^{{\frac {1}{\nu }}+1}}}\\\end{aligned}}} COVID-19 감염 궤적 모델링 리차드 성장 곡선이라고도 불리는 일반화된 로지스틱 함수는 COVID-19 감염 궤적을 모델링하는 데 널리 사용된다.[2] 감염 궤적은 국가, 도시, 주 등과 같은 대상의 누적 감염자 수에 대한 일일 시계열 데이터다. 문헌에는 변형된 재변수가 있다: 자주 사용되는 형태 중 하나는
f ( t ; θ 1 , θ 2 , θ 3 , ξ ) = θ 1 [ 1 + ξ 생략하다 ( − θ 2 ⋅ ( t − θ 3 ) ) ] 1 / ξ {\displaystyle f(t;\theta _{1},\theta _{2},\theta _{3},\xi )={\frac {\fracta _{1}{1}{1+\xi \expect\cdot (t-\teta _{3})^{1/\xi }}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} 여기서 θ 1 θ 2 θ {\ displaystyle \theta _{1},\theta _{2},\theta _{3} ξ {\displaystyle \xi} 원곡선 displaystyle 파라미터 { displaystyle xi 1 displaysty xi {\displaysty \xi} 곰퍼츠 함수 로 수렴되기 때문이다 역학 모델링에서 θ 1 {\ displaystyle \theta_{1 2 {\ displaystyle \theta_{2 , 3 {\ displaystyle \theta_{3} (10 , 000 , 0 , 40 {\displaystyle (\theta _{1},\theta _{2},\theta _{3}) (가 감염 .
COVID-19 및 5월 14일까지 총(인구) 평균으로 심각한 영향을 받은 40개국의 감염 궤적 외삽 역학 모델링에서 일반화된 로지스틱 기능 과 같은 성장 기능을 사용할 때의 이점 중 하나는 성장 기능을 사용하여 여러 과목(국가, 도시, 주 등)의 감염 궤적을 설명함으로써 다단계 모델 프레임워크로 비교적 쉽게 확장된다는 것이다. 위의 그림을 참조하십시오. 이러한 모델링 프레임워크는 비선형 혼합 효과 모델 또는 계층적 비선형 모델이라고도 한다.
특례 다음 함수는 리차드 곡선의 구체적인 사례들이다.
참조 Richards, F. J. (1959). "A Flexible Growth Function for Empirical Use". Journal of Experimental Botany 10 (2): 290–300. doi :10.1093/jxb/10.2.290 . Pella, J. S.; Tomlinson, P. K. (1969). "A Generalised Stock-Production Model". Bull. Inter-Am. Trop. Tuna Comm . 13 : 421–496. Lei, Y. C.; Zhang, S. Y. (2004). "Features and Partial Derivatives of Bertalanffy–Richards Growth Model in Forestry". Nonlinear Analysis: Modelling and Control . 9 (1): 65–73. doi :10.15388/NA.2004.9.1.15171 . 






























![{\displaystyle f(t;\theta _{1},\theta _{2},\theta _{3},\xi )={\frac {\theta _{1}}{[1+\xi \exp(-\theta _{2}\cdot (t-\theta _{3}))]^{1/\xi }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29479f9d2bb480d1bf104fc0d84fcbaf00cf99f6)
 실수이며,
실수이며,  양수 실수다.
양수 실수다.  곡선이 로지스틱 함수로 감소하고, ii
곡선이 로지스틱 함수로 감소하고, ii 








