헵토미노

Heptomino
108 프리 헵토미노

헵토미노(또는 7-미노)는 7차 폴리오미노, 즉 모서리끼리 연결된 [1]7개의 동일한 크기의 정사각형으로 이루어진 평면 내의 폴리곤입니다.이 유형의 그림의 이름은 접두사 hept(a)-로 형성됩니다.회전과 반사가 뚜렷한 모양으로 간주되지 않을 경우, 108개의 다른 자유 헵토미노가 있습니다.반사가 구별된다고 간주할 때, 196개의 단측 헵토미노가 있다.회전도 구별되는 것으로 간주할 때 고정 헵토미노는 [2][3]760개입니다.

대칭

그림은 대칭 그룹에 따라 색칠된 가능한 모든 유리 헵토미노를 보여준다.

  • 84개의 헵토미노(회색)는 대칭이 없습니다.대칭 그룹은 오직 아이덴티티 매핑으로만 구성됩니다.
  • 9개의 헵토미노(빨간색)는 격자선에 정렬된 반사 대칭축을 가진다.대칭 그룹에는 정사각형의 변에 평행한 선의 동일성과 반사라는 두 가지 요소가 있습니다.
Reflection Symmetrical Heptominoes-90-deg.svg
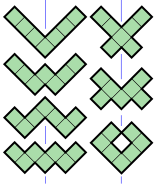
  • 7개의 헵토미노(녹색)는 격자선에 대해 45°의 반사 대칭 축을 가진다.대칭 그룹에는 동일성과 대각선 반사라는 두 가지 요소가 있습니다.
Reflection Symmetrical Heptominoes-45-deg.svg
  • 4개의 헵토미노(파란색)는 2차 회전 대칭이라고도 하는 점 대칭을 가지고 있습니다.대칭 그룹에는 항등식과 180° 회전이라는 두 가지 요소가 있습니다.
Rotation Symmetrical Heptominoes.svg
  • 3개의 헵토미노(보랏빛)는 두 개의 반사 대칭 축을 가지며, 둘 다 격자선과 정렬됩니다.대칭 그룹에는 4개의 요소, 즉 동일성, 2개의 반사 및 180° 회전이 있습니다.클라인 4군이라고도 하는 2차 2면체 군입니다.
  • 1 헵토미노(주황색)에는 대각선과 정렬된 두 개의 반사 대칭 축이 있습니다.대칭 그룹도 4개의 요소를 가지고 있습니다.대칭군은 또한 4개의 원소가 있는 2차 2면체 군이다.
Rotation and Reflection Symmetrical Heptominoes.svg

단측 헵토미노와 마찬가지로 헵토미노의 반사가 구별되는 것으로 간주될 경우, 위의 첫 번째와 네 번째 범주는 각각 크기가 두 배로 증가하여 총 196개의 헵토미노 88개가 추가된다.회전도 구별되는 것으로 간주될 경우 첫 번째 카테고리의 헵토미노는 8배, 다음 세 카테고리의 헵토미노는 4배, 마지막 두 카테고리의 헵토미노는 2배입니다.그 결과 84 × 8 + (9+7+4) × 4 + (3+1) × 2 = 760 고정 헵토미노가 된다.

포장 및 타일링

108개의 유리 헵토미노 중 101개가 콘웨이 기준을 충족하고 3개가 더 기준을 충족하는 패치를 형성할 수 있다.따라서 4개의 헵토미노만 기준을 충족하지 못하고 실제로 이들 4개는 [4]평면을 테셀링할 수 없다.

타일을 칠 수 없는 네 개의 헵토미노는 구멍이 뚫린 헵토미노를 포함해서

자유 헵토미노 108개의 전체 세트가 총 756개의 정사각형을 가지고 있지만, 이 세트로 직사각형을 타일링할 수는 없습니다.구멍이 [5]뚫린 헵토미노가 한 개 있기 때문에 그 증거는 간단하다.또한 757은 소수이기 때문에 1제곱 홀이 있는 757제곱 직사각형 안에 그것들을 넣는 것도 불가능하다.

그러나 단순히 연결된 107개의 무료 헵토미노 세트(즉, 구멍이 없는 107개의 직사각형)는 7x107개의 [6]타일을 만들 수 있습니다.또한 자유 헵토미노 전 세트는 각각 중앙에 1제곱홀이 있는 11×23(253제곱) 직사각형 3개를 타일링할 수 있으며, 전체 세트는 "중앙"[7]에 1제곱홀이 있는 8×8(64제곱) 정사각형 12개를 타일링할 수도 있다.

레퍼런스

  1. ^ Golomb, Solomon W. (1994). Polyominoes (2nd ed.). Princeton, New Jersey: Princeton University Press. ISBN 0-691-02444-8.
  2. ^ Weisstein, Eric W. "Heptomino". From MathWorld – A Wolfram Web Resource. Retrieved 2008-07-22.
  3. ^ Redelmeier, D. Hugh (1981). "Counting polyominoes: yet another attack". Discrete Mathematics. 36 (2): 191–203. doi:10.1016/0012-365X(81)90237-5.
  4. ^ Rhoads, Glenn C. (2005). "Planar tilings by polyominoes, polyhexes, and polyiamonds". Journal of Computational and Applied Mathematics. 174 (2): 329–353. doi:10.1016/j.cam.2004.05.002.
  5. ^ Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman and Company. ISBN 0-7167-1193-1.
  6. ^ "폴리미노:더 많은 헵토미노!
  7. ^ 이미지 패트릭 햄린의 놀라운 헵토미노 솔루션 2001년 2월부터 8월까지 Material에서 MathPuzzzle.com에 추가