파로 셔플

이 글의 리드 섹션은 요점을 적절히 요약하기에는 너무 짧을 수 있다. 기사의 모든 중요 측면에 대한 액세스 가능한 개요를 제공하도록 리드를 확장하는 것을 고려하십시오(2018년 10월).

파로 셔플(미국식), 짜는 셔플(영국식), 또는 도브테일 셔플(dobtail shuffle)은 카드를 섞는 방법인데, 카드 절반은 엄지손가락을 안쪽으로 하여 손에 쥐고 있다가 카드가 엄지손가락에 의해 풀어져 인터리브 테이블로 떨어진다.디아코니스, 그레이엄, 칸토르도 이것을 마법에 사용할 때 기술이라고 부른다.^[1]

수학자들은 "faro shuffle"이라는 용어를 사용하여 데크를 26장의 같은 카드 더미로 정확하게 재배열한 다음 완벽하게 결합된다.^[2]

설명

오른손잡이 시술자는 왼손에는 위, 오른손에는 아래에서 카드를 잡는다.데크는 오른손 엄지손가락으로 카드 반을 살짝 들어올리고 왼손의 패킷을 오른손에서 앞으로 밀어내는 것만으로 선호되는 두 부분으로 분리된다.두 패킷은 서로 교차하여 두드려 정렬하는 경우가 많다.그리고 나서 그들은 짧은 면에 함께 밀리고 위아래로 구부러진다.그러면 카드는 서로 번갈아 떨어지게 되고, 지퍼처럼 서로 하나씩 교대하는 것이 이상적이다.압력을 가하여 패킷을 함께 스프링하고 위에서 아래로 구부려 줌으로써 번성함을 더할 수 있다.^[3]

파로 게임은 딜러가 다음 게임을 위해 카드를 결합해야 하는 두 개의 동일한 쌓기로 끝난다.마술사 존 매스클린의 말에 따르면, 위와 같은 방법이 사용되었고, 그는 그것을 "파로 딜러의 셔플"^[4]이라고 부른다.마스켈리네가 가장 먼저 명확한 지시를 내렸으나, 셔플은 수학자이자 마술사 페르시 디아콘리스에 의해 대부분 발견되었듯이 일찍이 파로와 관련되었다.^[5]

퍼펙트 슈플

원래 상단 카드는 맨 위에, 하단 카드는 맨 아래에 두는 파로 셔플은 아웃 셔플(out-shuffle)으로 알려져 있으며, 원래 상단 카드는 두 번째로, 하단 카드는 두 번째로 이동하는 파로 셔플은 인 셔플(in-shuffle)로 알려져 있다.이 이름들은 마술사와 컴퓨터 프로그래머인 알렉스 엘름슬리에 의해 만들어졌다.^[6]카드가 완벽하게 번갈아 나오는 완벽한 파로 셔플은 셔플러가 데크를 두 개의 동일한 스택으로 자르고 서로 하프 데크를 밀어 넣을 때 적절한 압력을 가해야 한다.

faro shuffle은 덱을 완전히 무작위화하지 않는 제어된 shuffle이다.완벽한 인슈플레를 구사할 수 있다면 26개의 슈플이 갑판 순서를 뒤바꾸고 26개를 더하면 원래의 순서로 복원된다.^[7]

In general, ${\displaystyle k}$ perfect in-shuffles will restore the order of an ${\displaystyle n}$-card deck if ${\displaystyle 2^{k}\equiv 1{\pmod {n+1}}}$. For example, 52 consecutive in-shuffles restore the order of a 52-card deck, because ${\displaystyle 2^{5$$2}\equiv$ 1${\pmod{53$

In general, ${\displaystyle k}$ perfect out-shuffles will restore the order of an ${\displaystyle n}$-card deck if ${\displaystyle 2^{k}\equiv 1{\pmod {n-1}}}$. For example, if one manages to perform eight out-shuffles in a row, then the deck of 52 cards will be restored to its original order, because $2{\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {8\mathrm{}}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle 1}$(${\displaystyle \mathrm{모드}}$ ${\displaystyle 51}$) ${\$ 1${\pmod{51$ 그러나 64 카드 덱의 순서를 복원하려면 6개의 faro out-shuffle만 필요하다.

즉, 짝수 N 크기의 카드 데크를 원래의 순서로 되돌리는 데 필요한 슈플의 수는 2모듈로(N + 1)의 승수 순서에 의해 주어진다.

예를 들어, N = 2, 4, 6, 8, 10, 12 ...의 데크 크기의 경우 필요한 슈플의 수는 2, 4, 3, 6, 10, 12, 4, 8, 18, 6, 11, ...(OEIS에서 순차 A002326)이다.

원시 뿌리에 대한 아르틴의 추측에 따르면, 완전한 n 슈플 세트가 필요한 데크 사이즈가 무한히 많다는 것을 따른다.^[8]

무한 시퀀스에 대한 아웃 셔플과 유사한 작동은 인터리브 시퀀스다.

예

간단히 말하자면, 우리는 6장의 카드를 사용할 것이다.

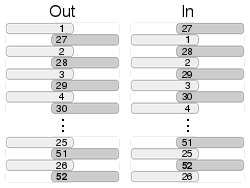
다음은 인슈플레를 각각 섞은 후의 데크 순서를 보여준다.이 크기의 갑판은 3번 셔플 후에 원래 순서로 돌아온다는 점에 유의하십시오.

스텝	톱 카드	2	3	4	5	밑단 카드
시작
1
2
3

다음은 각 아웃슈플 후의 데크 순서를 보여준다.이 크기의 데크는 4번 셔플아웃한 후에 원래 순서로 돌아온다는 점에 유의하십시오.

스텝	톱 카드	2	3	4	5	밑단 카드
시작
1
2
3
4

갑판조작으로

마술사 알렉스 엘름슬리는 갑판의 상단 카드를 원하는 위치로 이동시키기 위해 제어된 일련의 내부 및 외부 셔플을 사용할 수 있다는 것을 발견했다^{[citation needed]}.카드의 원하는 위치를 이진수로 표현한 뒤 각 1에 인슈플레를, 각 0에 아웃슈플을 하는 게 요령이다.

예를 들어, 상위 카드를 10개의 카드가 있도록 아래로 이동하려면 숫자 10을 이진수(1010₂)로 표시하십시오.안으로, 밖으로, 안으로, 밖으로, 밖으로.카드 열 장을 갑판 위에서 떨어뜨려라. 열한 번째 카드가 너의 원래 카드가 될 것이다.숫자 10을 1010으로₂ 표현하든 00001010으로₂ 표현하든 상관 없다는 점에 유의하십시오. 아웃슈플은 항상 상위 카드를 유지하므로 예비 아웃슈플은 결과에 영향을 주지 않는다.

집단 이론 측면

수학에서 완벽한 섞임은 대칭 그룹의 요소로 간주될 수 있다.

보다 일반적으로 $S{\displaystyle {}_{}}$ ${\displaystyle {\mathrm{2n}}_{}}$ ${\$에서 완벽한 셔플은 세트를 2개의 더미로 분할하여 중간으로 만드는 순열이다.

${\displaystyle S_{2n}}$=${\displaystyle {\begin{pmatrix}1&2&3&4&\cdots &2n-1&2n\\1&n+1&2&n+2&\cdots &n&2n\end{pmatrix}}}$

즉, 지도라는 것이다.

${\displaystyle k\mapsto {\reases}{\frac {k+1}{{2}}&k\{\text{n1}\n+{k}{2}}&k\{\text{ven}}\case}}}}}}}}$

이와 유사하게${\displaystyle }$(${\displaystyle k}$, ${\displaystyle n}$) ${\displaystyle (k,n)}$ -완벽한$$ 셔플 순열은^[9] Sk n ${\$의 원소로서 세트를$$ k 더미로 분할하여 절개한다.

$({\displaystyle }$$2{\displaystyle {}_{}}$${\displaystyle }$, ${\displaystyle n}$) ${\$$displaystyle$$(2,n)}$ -완벽한$$ 셔플, ${\displaystyle \mathrm{\rho n}}$ ${\displaystyle \{\backslash }$$displaystyle \$${\displaystyle \mathrm{rho\_}}$${n$는 (${\displaystyle 2}$, n${\displaystyle }$- 1)${\displaystyle ($2$,n-1)$ -완벽한$$ $셔플$의 구성으로 n ${\$ $n}$ -cyle$$$$$\rho_{n$:

${\displaystyle {\mbox{sgn}}(\rho _{n}=(1-1)^{n+1}{\mbox{sgn}}(\rho _{n-1}).}$

따라서 기호는 4주기적이다.

${\displaystyle{\mbox{sgn}}(\rho _{n})=-1)^{\lfloor n/2\nloor }={\pmod}+1&n\equiv 0,1}{\pmod{4}}}}\pmod{4}}}}}}}}}}}}case}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

처음 몇 가지 완벽한 셔플은 다음과 같다$$:$$ 0 {\$displaystyle \rho_{0}$과 $\$ 1 {\$displaystyle$ \$rho_$${1}{$$1$}}은$$ 사소한 것이고,${\displaystyle {}_{}}$ 2$${\$displaystyle$$\rho_{$2}}은$$ 전이${\displaystyle }$(${\displaystyle 23}$) $S_{4}$이다$.$

메모들

참조

• Diaconis, P.; Graham, R. L.; Kantor, W. M. (1983). "The mathematics of perfect shuffles" (PDF). Advances in Applied Mathematics. 4 (2): 175–196. doi:10.1016/0196-8858(83)90009-X.

• Ellis, J.; Fan, H.; Shallit, J. (2002). "The Cycles of the Multiway Perfect Shuffle Permutation" (PDF). Discrete Mathematics and Theoretical Computer Science. 5: 169–180. doi:10.46298/dmtcs.308. Retrieved 26 Dec 2013.

• Maskelyne, John (1894). Sharps and Flats: A Complete Revelation of the Secrets of Cheating at Games of Chance and Skill. Longmans, Green and Company. Retrieved 26 Dec 2013.

• Morris, S. Brent (1998). Magic Tricks, Card Shuffling, and Dynamic Computer Memories. The Mathematical Association of America. ISBN 0-883-85527-5. Retrieved 26 Dec 2013.

• Kolata, Gina (April 1982). "Perfect Shuffles and Their Relation to Math". Science. 216 (4545): 505–506. Bibcode:1982Sci...216..505K. doi:10.1126/science.216.4545.505. PMID 17735734.
• Jain, Peiyush (May 2008). "A simple in-place algorithm for in shuffles". arXiv:0805.1598 [cs.DS].