영향도

영향도(ID)는 의사결정 상황을 압축적으로 그래픽으로 수학적 방법으로 나타낸 것이다. 확률론적 추론 문제뿐 아니라 (최대 기대 효용 기준에 따른) 의사결정 문제도 모델링하고 해결할 수 있는 베이시안 네트워크의 일반화다.

ID는 이해하기 쉬운 직관적인 의미론을 가진 의사결정 분석가들에 의해 1970년대 중반에 처음 개발되었다. 현재 광범위하게 채택되어 각 변수를 모델링한 분기의 수가 기하급수적으로 증가하는 의사결정 트리의 대안이 되고 있다. ID는 팀원 간의 불완전한 정보 공유를 명시적으로 모델링하고 해결할 수 있기 때문에 팀 의사결정 분석에서 직접 적용할 수 있다. ID의 확장 또한 게임 트리의 대체 표현으로서 게임 이론에서 그들의 용도를 찾는다.

의미론

ID는 세 가지 유형의 노드(하위 유형 1개 포함)와 노드 사이에 세 가지 유형의 호(또는 화살표)를 가진 방향 AC순환 그래프다.

노드:

• 의사결정 노드(각 의사결정에 대응)는 직사각형으로 그려진다.
• 불확실성 노드(모델화할 각 불확실성에 대응)는 타원형으로 그려진다.

• 결정론적 노드(일부 다른 불확실성의 결과가 알려질 때마다 결정적으로 그 결과가 알려져 있다는 특수한 종류의 불확실성에 대응함)는 이중 타원형으로 그려진다.

• 값 노드(추가적으로 분리 가능한 Von Neumann-Morgenstern 유틸리티 함수의 각 구성요소에 대응함)는 8각형(또는 다이아몬드)으로 그려진다.

호:

• 기능 호(값 노드 끝)는 부가적으로 분리 가능한 효용 함수의 구성요소 중 하나가 꼬리에 있는 모든 노드의 함수임을 나타낸다.
• 조건부 호(불확실성 노드에서 종료)는 머리 부분의 불확실성이 꼬리 부분의 모든 노드에서 확률적으로 조건화되었음을 나타낸다.

• 조건부 호(결정론적 노드에서 종료)는 머리 부분의 불확실성이 꼬리에 있는 모든 노드에서 결정적으로 조건화됨을 나타낸다.

• 정보 호(결정 노드에서 종료)는 모든 노드의 꼬리에 있는 결과를 미리 알고 머리에서 결정을 내린다는 것을 나타낸다.

적절한 구조 ID 지정:

• 의사결정 노드 및 들어오는 정보 호는 대안을 집합적으로 명시한다(특정 결정 및/또는 불확실성의 결과가 사전에 알려진 경우 수행할 수 있는 조치).
• 불확실성/결정론적 노드 및 들어오는 조건부 호는 정보를 집합적으로 모델링(알고 있는 것과 그 확률론적/결정론적 관계
• 가치 노드와 들어오는 기능 호는 선호도(사물이 서로 선호되는 방식)를 집합적으로 정량화한다.

대안, 정보 및 선호도는 의사결정 분석에서 의사결정 기반이라고 불리며, 유효한 의사결정 상황에서 세 가지 필수 구성요소를 나타낸다.

형식적으로 영향도의 의미도는 노드와 호를 순차적으로 구성하는 것에 기초하며, 이는 다이어그램의 모든 조건부 독립성의 사양을 내포하고 있다. 규격은 베이시안 네트워크의 $d{\displaystyle }$ ${\displaystyle d}$ -분리$$ 기준으로 정의된다. 이 의미론에 따르면, 모든 노드는 이전의 직계 노드의 결과를 고려할 때 비 프로세서 노드에서 확률적으로 독립적이다. 마찬가지로 비값 노드 $X{\displaystyle }$ ${\displaystyle X}$과(와) 비값 노드 $Y{\displaystyle }$ ${\displaystyle Y}$ 사이에 호가 누락된 경우$$, $ou{\displaystyle }$}에$$ 지정된 $X{\displaystyle }$ ${\displaystyle$ $X$$}$과$($$와{\displaystyle }$) 독립적으로$$ $Y{\displaystyle }$ ${\displaystyty$ Y$}$을 렌더링하는 비값 노드 Z ${\\displaystystystystytype$ Z}이$있음$을 의미한다.$Z{\displaystyle }$ ${\displaystyle$ Z$\}$에 있는 노드의 반환.

예

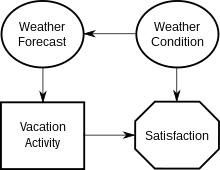
의사결정자가 휴가를 계획하고 있는 상황을 나타내는 간단한 영향도도를 고려해보자.

• 의사결정 노드(Vacation Activity), 불확실성 노드 2개(Weather Condition, Weather Forecast), 가치 노드 1개(만족)가 있다.
• 기능 호 2개(만족에서 종료), 조건 호 1개(기상 예측에서 종료), 정보 호 1개(휴가 활동에서 종료)가 있다.

• 만족으로 끝나는 기능 호는 만족도가 날씨 조건과 휴가 활동의 효용 함수임을 나타낸다. 즉, 날씨가 어떠한지, 활동 선택이 어떤지를 알면 만족도를 수치화할 수 있다.(기상 예측을 직접적으로 중요시하지 않는다는 점에 유의)
• 일기예보에서 끝나는 조건부 호는 일기예보와 기상조건이 좌우될 수 있다는 그들의 믿음을 나타낸다.
• 휴가 활동으로 끝나는 정보 호는 그들이 선택할 때 날씨 조건이 아닌 일기 예보만 알게 된다는 것을 나타낸다. 즉, 실제 날씨는 그들이 선택을 한 후에 알 수 있을 것이고, 오직 예측만이 그들이 현 단계에서 믿을 수 있는 것이다.

• 예를 들어, 휴가 활동이 (기상 예측과 관련 없는) 날씨 조건에 독립적이라는 것도 의미론적으로 뒤따른다.

정보의 가치에 대한 적용 가능성

위의 예는 정보의 가치라고 알려진 의사결정 분석에서 극히 중요한 개념을 나타내는 영향도의 힘을 강조한다. 다음 세 가지 시나리오를 고려하십시오.

• 시나리오 1: 의사결정자는 날씨 상태가 어떨지 아는 동안 휴가 활동 결정을 내릴 수 있다. 이는 위의 영향 다이어그램에서 날씨 조건으로부터 휴가 활동에 추가 정보 호를 추가하는 것과 일치한다.
• 시나리오 2: 위와 같은 원래의 영향도.
• 시나리오 3: 의사결정자는 일기 예보도 모른 채 결정을 내린다. 이는 위의 영향력 다이어그램에서 날씨 예측에서 휴가 활동으로 정보 호를 제거하는 것과 일치한다.

시나리오 1은 결정을 내릴 때 (기상 조건)에 대해 더 이상 불확실하지 않기 때문에 이 결정 상황에 대해 가능한 최선의 시나리오다. 그러나 시나리오 3은 (기상조건)에 대해 어떤 암시도 없이 (기상전망) 결정을 내려야 하기 때문에 이번 결정 상황에는 최악의 시나리오다.

의사결정자는 일반적으로 새로운 정보의 획득을 통해 시나리오 3에서 시나리오 2로 이동하는 것이 더 낫다(평균적으로 더 나쁘지는 않다). 그들이 그러한 움직임에 대해 기꺼이 지불해야 할 가장 많은 것을 일기예보에 관한 정보의 가치라고 하는데, 이것은 본질적으로 일기조건에 대한 불완전한 정보의 가치다.

마찬가지로 의사결정자가 시나리오 3에서 시나리오 1로 이동하는 것이 최선이다. 그들이 그러한 움직임에 대해 기꺼이 지불해야 할 가장 큰 것은 날씨 상태에 대한 완벽한 정보의 가치라고 불린다.

이 단순한 ID의 적용가능성과 정보개념의 가치는, 특히 대부분의 의사결정이 그들의 환자, 질병 등에 대한 불완전한 정보로 이루어져야 할 때, 의료적 의사결정에 있어서, 엄청나다.

관련개념

영향력 도표는 계층적이며, 구조상 또는 도표 요소들 사이의 기능적 및 수치적 관계 측면에서 보다 상세하게 정의할 수 있다. 구조, 기능, 숫자 등 모든 수준에서 일관되게 정의되는 ID는 잘 정의된 수학적 표현이며, 잘 형성된 영향도(WFID)라고 한다. WFID는 많은 종류의 확률론적, 고려적, 의사결정 질문에 대한 답을 도출하기 위해 반전 및 제거 연산을 사용하여 평가할 수 있다. 베이지안 네트워크 추론(믿음 전파)에 관한 인공지능 연구자들에 의해 보다 최근의 기법이 개발되었다.

불확실성 노드(즉, 베이시안 네트워크)만 있는 영향도를 관련도라고 부르기도 한다. 노드 A와 B를 연결하는 호는 "A가 B와 관련됨"을 의미할 뿐만 아니라 "B가 A와 관련됨"(즉, 관련성은 대칭 관계)을 의미한다.

참고 항목

참고 문헌 목록

• Detwarasiti, A.; Shachter, R.D. (December 2005). "Influence diagrams for team decision analysis" (PDF). Decision Analysis. 2 (4): 207–228. doi:10.1287/deca.1050.0047.
• Holtzman, Samuel (1988). Intelligent decision systems. Addison-Wesley. ISBN 978-0-201-11602-1.
• Howard, R.A. 및 J.E. Mathesson, "인플레이언스 다이어그램"(1981)의 의사결정 분석의 원리 및 적용에 관한 리딩에서, R.A. Howard와 J.E. Matheson, Vol. II(1984), Menlo Park CA: 전략적 의사결정 그룹.
• Koller, D.; Milch, B. (October 2003). "Multi-agent influence diagrams for representing and solving games" (PDF). Games and Economic Behavior. 45: 181–221. doi:10.1016/S0899-8256(02)00544-4.
• Pearl, Judea (1988). Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Representation and Reasoning Series. San Mateo CA: Morgan Kaufmann. ISBN 0-934613-73-7.
• Shachter, R.D. (November–December 1986). "Evaluating influence diagrams" (PDF). Operations Research. 34 (6): 871–882. doi:10.1287/opre.34.6.871.
• Shachter, R.D. (July–August 1988). "Probabilistic inference and influence diagrams" (PDF). Operations Research. 36 (4): 589–604. doi:10.1287/opre.36.4.589. hdl:10338.dmlcz/135724.
• Virine, Lev; Trumper, Michael (2008). Project Decisions: The Art and Science. Vienna VA: Management Concepts. ISBN 978-1-56726-217-9.
• Pearl, J. (1985). Bayesian Networks: A Model of Self-Activated Memory for Evidential Reasoning (UCLA Technical Report CSD-850017). Proceedings of the Seventh Annual Conference of the Cognitive Science Society 15–17 April 1985. http://ftp.cs.ucla.edu/tech-report/198_-reports/850017.pdf., University of California, Irvine, CA. pp. 329–334. Retrieved 2010-05-01. {{cite conference}}: 외부 링크 위치 conference= (도움말)

외부 링크

• 영향도란 무엇인가?
• Pearl, J. (December 2005). "Influence Diagrams — Historical and Personal Perspectives" (PDF). Decision Analysis. 2 (4): 232–4. doi:10.1287/deca.1050.0055.