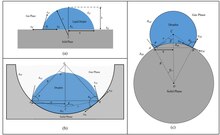
접촉각

소수성으로 처리된 천은 높은 접촉각을 보인다.

접촉각은 액체-증기 계면이 고체 표면과 만나는, 일반적으로 액체를 통해 측정되는 각도입니다.영 방정식을 통해 액체에 의한 고체 표면의 습윤성을 정량화합니다.주어진 온도와 압력에서 주어진 고체, 액체 및 증기의 시스템은 고유한 평형 접촉각을 가진다.그러나 실제로는 전진(최대) 접촉각에서 후퇴(^[1]최소) 접촉각까지 다양한 접촉각 이력 동적인 현상이 종종 관찰된다.평형 접촉은 이 값들 안에 있고, 그것들로부터 계산할 수 있다.평형 접촉각은 액체, 고체 및 증기 분자 상호작용의 상대적 강도를 반영한다.

접촉 각도는 액체의 자유 표면 위에 있는 매체, 접촉하는 액체와 고체의 특성에 따라 달라집니다.액체 표면에 대한 고체의 기울기와는 무관합니다.표면 장력에 따라 변하며, 따라서 액체의 온도와 순도에 따라 변합니다.

열역학

영 방정식의 양을 나타내는 액체 방울의 도식.

액체-증기 계면의 모양은 영-듀프레 방정식에 의해 결정되며, 접촉 각도는 영 방정식을 통해 경계 조건의 역할을 한다.

접촉에 대한 이론적 설명은 세 가지 상, 즉 액체 상(L), 고체 상(S), 기체 또는 기상 상(G) 사이의 열역학적 평형을 고려함으로써 발생한다(주변 대기와 액체 증기의 평형 농도의 혼합일 수 있음).('가스' 단계는 또 다른 불용성 액상으로 대체될 수 있습니다.)고체-증기 계면에너지가 $\gamma _{SG}$ S $\gamma _{SG}$ {\ $displaystyle \gamma$ _{SG $\gamma _{SG}$ 고체-액체 계면에너지가 $\gamma _{SL}$ $\gamma _{SL}$ L {\ $displaystyle \gamma$ _ ${$ $SL$ $\gamma _{SL}$ 액체-증기 계면에너지( $\gamma _{LG}$ )가 $\gamma _{LG}$ L G {\ $displaystyle$ $\gamma _{SL}$ \ $gamma$ 평형에너지가 if LG $}$ 이면 LG}이다. $(\$ _ ${\mathrm {C}})$ 는 $\theta_\mathrm{C}$ 영 방정식에 의해 다음 양으로부터 구한다.

\displaystyle _{\mathrm {SG}}-\display _{\mathrm {SL}-\display _{\mathrm {LG}}\cos \theta _{\mathrm {C} = 0,}

접촉각은 영-듀프레 방정식을 통한 접착 작용과도 관련될 수 있다.

{\mathrm {LG}}(1+\cos \theta _{\mathrm {C} })=\Delta W_{\mathrm {SLG} },

여기서 $\Delta W_{\mathrm {SLG} }$ W $\Delta W_{\mathrm {SLG} }$ $\Delta W_{\mathrm {SLG} }$ (\ $displaystyle \Delta W_{\mathrm {SLG}}})$ 는 $\Delta W_{\mathrm {SLG} }$ 단위 면적당 고체 액체 접착 에너지이다.

수정영 방정식

평평한 표면에 있는 물방울의 접촉각과 표면 장력 사이의 관계에 대한 최초의 연구는 1805년에 ^[2]토마스 영에 의해 보고되었다.한 세기 후^[3] 깁스는 접촉각의 부피 의존성을 설명하기 위해 영 방정식의 수정을 제안했다.깁스는 3상 경계에서 작용하고 고액-액상-가스상 계면의 합류에서 잉여 에너지를 설명하는 라인 장력의 존재를 가정하고 다음과 같이 구한다.

{\displaystyle \cos(\theta)={\frac{\gamma_{SG}-\gamma _{SL}}{\gamma_{LG}}}+{\frac{\kappa}{\gamma_{LG}}}{\frac{1}{를}}}.

어디 κ[N] 있는 행동을 긴장과 a[m]은 방울 됩니다.비록 실험 데이터에 닿을 각도의 코사인과 역 라인 반경 사이의 상관 관계를 증명할 수, κ의 정확한 간판과 양의 몇개 순서에 의해 그 가치가 잘난 줄 아설명하지 않는다.

라인 장력과 라플라스 압력을 고려하면서 접촉각 예측

기본 다이어그램 평평한(를)오목(b)와 볼록(c)surfaces[4]에 물방울들.

원자력 현미경, 공초점 현미경과 주사 전자 현미경 같은 측정 기술의 개선으로 연구원과 이미지를 더욱 더 작은 규모에서 물방울들을 생산할 수 있었다.로 입자 크기의 감소에 오줌의 새로운 실험적 관찰했다.이러한 관찰자가 지정된 영의 방정식은 micro-nano 비늘을 수용하지 않음을 확인했다.Jasper[5][4] 그러한 작은 비늘에서 각도 문제를 해결하는 것은 자유 에너지 변화에 VdP 용어 포함한 열쇠일지 모르겠다고 제안했다.자유 에너지의 변화 균형에서 0이다:.

0={\frac{dA_{LG}}{dA_{SL}}}+{\frac{\gamma_{SL}-\gamma _{SG}}{\gamma_{LG}}}-{\frac{\kappa}{\gamma_{LG}}}{\frac{dL}{dA_{SL}}}-{\frac{V}{\gamma_{LG}}}{\frac{dP}{dA_{SL}}}

자유 액체-증기 경계에서 압력의 변화는 평균 곡률에 비례하는 라플라스 압력 때문이다.볼록 표면과 오목 표면 모두에 대해 위의 방정식을 풀면 다음과 같은 ^[4]결과가 나옵니다.

\displaystyle \cos(\theta \mp \alpha)=A+B{\frac {cos(\alpha)}{a}\pm C\sin(\theta \mp \alpha)\cos(\theta)+1)^2}{\biggl(}{\frac {sin(\alpha)\cos(\alpha)+2)}{(\cos(\alpha)+1)^2}}\mp {\frac {sin(\theta)\cos(\theta)+2)}{(\cos(\theta)+1)^2}}{\biggr}}}

$B={\frac {\kappa }{\gamma _{LG}}}$ 서 A $A={\frac {\gamma _{SG}-\gamma _{SL}}{\gamma _{LG}}}$ $A={\frac {\gamma _{SG}-\gamma _{SL}}{\gamma _{LG}}}$ S $A={\frac {\gamma _{SG}-\gamma _{SL}}{\gamma _{LG}}}$ G - $A={\frac {\gamma _{SG}-\gamma _{SL}}{\gamma _{LG}}}$ S L $A={\frac {\gamma _{SG}-\gamma _{SL}}{\gamma _{LG}}}$ L G $A={\frac {\gamma _{SG}-\gamma _{SL}}{\gamma _{LG}}}$ L G = $fr$ frac $_$ { $SL$ } } { \ $gamma _$ { $A={\frac {\gamma _{SG}-\gamma _{SL}}{\gamma _{LG}}}$ LG } $A={\frac {\gamma _{SG}-\gamma _{SL}}{\gamma _{LG}}}$ } 、 $B={\frac {\kappa }{\gamma _{LG}}}$ $B={\frac {\kappa }{\gamma _{LG}}}$ $B={\frac {\kappa }{\gamma _{LG}}}$ L $B={\frac {\kappa }{\gamma _{LG}}}$ = $ac$ L G $B={\frac {\kappa }{\gamma _{LG}}}$ （ $displaystyle$ B ）（ \ $appa }$ } $C={\frac {\gamma }{3\gamma _{LG}}}$ C $B={\frac {\kappa }{\gamma _{LG}}}$ }

이 방정식은 접촉각, 벌크 열역학에 대한 세실 물방울의 기하학적 특성, 3상 접촉 경계의 에너지 및 물방울의 평균 곡률을 관련짓습니다. $(\alpha =0)$ 한 $(\alpha =0)$ 표면에 세실 물방울이 있는 특수한 경우( $(\alpha =0)$ $(\alpha =0)$ 0 $){displaystyle (\alpha = 0$

{\displaystyle \cos(\theta)=slac {\gamma _{LG}}+{\gamma _{LG}}{\frac {1}{a}-{\frac {3\gama}-{\ta}+cos(2)

위의 방정식에서 처음 두 항은 수정된 영의 방정식이고, 세 번째 항은 라플라스 압력에 의한 것입니다.이 비선형 방정식은 θ의 부호 및 크기, 매우 작은 척도의 접촉각 평탄화, 접촉각 이력 등을 정확하게 예측한다.

접촉각 이력

주어진 기판-액체-증기 조합은 실제로 연속적인 범위의 접촉각 값을 산출한다.최대 접촉각은 전진 접촉각, 최소 접촉각은 후퇴 접촉각이라고 합니다.전진 및 후퇴 접각은 물방울 또는 액체 브릿지가 ^[1]움직이는 동적 실험을 통해 측정됩니다.반면 영-라플라스 방정식으로 기술된 평형 접촉각은 정적 상태에서 측정된다.정적 측정은 퇴적 파라미터(예: 속도, 각도 및 낙하 크기)와 낙하 이력(예: 퇴적 시 증발)에 따라 전진 및 후퇴 접점 각도 사이의 값을 산출합니다.접촉각 이력서는 A $\theta _{\mathrm {A} }-\theta _{\mathrm {R} }$ - $\theta _{\mathrm {A} }-\theta _{\mathrm {R} }$ R $\theta _{\mathrm {A} }-\theta _{\mathrm {R} }$ \ $displaystyle \theta$ _ { \ $mathrm$ { $A }$ - \ $theta$ _ { \ $mathrm$ { $R }$ } 로 $\theta _{\mathrm {A} }-\theta _{\mathrm {R} }$ 정의됩니다.단, 이 용어는 식 $\cos \theta _{\mathrm {R} }-\cos \theta _{\mathrm {A} }$ $\cos \theta _{\mathrm {R} }-\cos \theta _{\mathrm {A} }$ R $\cos \theta _{\mathrm {R} }-\cos \theta _{\mathrm {A} }$ - $\cos \theta _{\mathrm {R} }-\cos \theta _{\mathrm {A} }$ A $\cos \theta _{\mathrm {R} }-\cos \theta _{\mathrm {A} }$ \ $displaystyle$ \ $cos$ \ $ta$ _ \ $mathrm$ { R } 로도 사용됩니다.애플리케이션에 따라 평형 접촉각 대신 정적, 전진 또는 후퇴 접촉각을 사용할 수 있습니다.전체적인 효과는 정적 마찰과 매우 유사한 것으로 볼 수 있다. 즉, 접촉선을 ^[6]이동하기 위해 단위 거리당 최소한의 작업량이 필요하다.

전진 접촉각은 액체-고체 응집력의 측정값으로 설명할 수 있으며 후퇴 접촉각은 액체-고체 접착력의 측정값이다.전진 및 후퇴 접각은 다른 방법을 사용하여 직접 측정할 수 있으며 힘 텐시메트리(일명 윌헤미-플레이트법)와 같은 다른 습윤 측정에서도 계산할 수 있습니다.

낙하물이 표면에서 직선적으로 움직이면 동일한 측정에서 진각과 후퇴각을 직접 측정할 수 있다.예를 들어 액체 방울은 정적 상태일 때는 주어진 접촉각을 채택하지만, 표면이 기울어지면 낙하와 표면 사이의 접촉 면적이 일정하게 유지되도록 처음에는 변형됩니다.드롭의 「다운힐」측에서는 높은 접촉각이 채용되고, 드롭의 「업힐」측에서는 낮은 접촉각이 채용됩니다.틸트 각도가 커짐에 따라 접촉 각도는 계속 변화하지만 낙하와 표면 사이의 접촉 면적은 일정하게 유지됩니다.주어진 표면 기울기 각도에서 전진 및 후퇴 접촉 각도가 충족되고 낙하물이 표면에서 움직입니다.실제로 틸트 속도가 높을 경우 전단력과 운동량의 영향을 받을 수 있습니다.측정방법은 접촉각 이력이 높은 시스템(30도 이상) 또는 낮은 시스템(10도 미만)에서도 실제로 어려울 수 있습니다.

표면에 퇴적된 물방울에 액체를 첨가 및 제거함으로써 접촉각의 진퇴를 측정할 수 있다.액체 방울에 충분한 양의 액체를 첨가해도 접점 라인은 핀으로 고정되고 접점 각도가 증가합니다.마찬가지로 액체 방울에서 소량의 액체를 제거하면 접촉각이 감소합니다.

영의 방정식은 균일한 표면을 가정하며 표면 텍스처나 중력과 같은 외부 힘을 고려하지 않습니다.실제 표면은 원자적으로 매끄럽지 않거나 화학적으로 균질하지 않기 때문에 낙하 시 접촉각 이력을 가정합니다.평형접각(θ $\theta _{\mathrm {c} }$ ${\displaystyle$ \ $theta$ _ ${\$ $mathrm$ $\theta _{\mathrm {c} }$ ${c$ $\theta _{\mathrm {c} }$ 은 Tadmor에^[7] 의해 이론적으로 제시되고 Chibski에^[8] 의해 실험적으로 확인된 ${\$ $\theta _{\mathrm {A} }$ {\ $displaystyle$ \ $theta$ {A $}}}$ 와 $\theta_\mathrm{A}$ ${\$ $\theta _{\mathrm {R} }$ {\ $displaystyle$ \ $theta$ { $R}$ 에서 $\theta_\mathrm{R}$ 계산할 수 있다.

\displaystyle \theta _{\mathrm {c} =\arccos \leftrm {A} } \cos \theta _{\mathrm {R} } +r_{\mathrm {R} } \cos \theta _{\mathrm {R}

어디에

r_{\mathrm {A}=\leftfrac {\sin ^{3}\theta _{\mathrm {A}}}}{2-3\cos \theta _{3}+\cos ^{{\mathrm {A}}}}}}\cos \cos \ta _{1/q} q

거칠거나 오염된 표면에는 접촉각 이력도 있지만, 이제 국소 평형 접촉각(영 방정식은 국소적으로만 유효)은 표면에 ^[9]따라 다를 수 있습니다.영-듀프레 방정식에 따르면 이는 접착 에너지가 국소적으로 변화함을 의미하며, 따라서 액체는 표면을 적시기 위해 국소 에너지 장벽을 극복해야 합니다.이러한 장벽의 결과 중 하나는 접촉각 이력입니다. 습윤의 정도, 따라서 관찰된 접촉각(접촉선을 따라 평균)은 액체가 표면에서 전진하는지 후퇴하는지에 따라 달라집니다.

액체는 이전에 건조한 표면에서 진행되지만 이전에 젖은 표면에서 후퇴하기 때문에 고체가 이전에 액체와 접촉(예: 화학 반응 또는 흡수에 의해)하여 변경된 경우에도 접촉각 이력이 발생할 수 있습니다.이러한 변화는 느리더라도 시간 의존적 접촉 각도를 측정할 수 있다.

접촉각에 대한 거칠기의 영향

표면 거칠기는 표면의 접촉각과 습도에 강한 영향을 미칩니다.거칠기의 영향은 물방울이 표면 홈을 적실지 또는 물방울과 표면 사이에 에어 ^[10]포켓이 남아 있을지에 따라 달라집니다.

표면이 균일하게 젖으면 물방울이 원젤 상태가 ^[11]된다.Wenzel 상태에서는 표면 거칠기를 추가하면 표면의 화학 작용으로 인한 습윤성이 향상됩니다.Wenzel 상관관계는 다음과 같이 기술할 수 있습니다.

\displaystyle \cos(\theta _{m})=r\cos(\theta _{Y})}

여기서 θ는_m 측정된 접촉각, θ는_Y 영 접촉각, r은 거칠기비입니다.거칠기 비율은 실제 표면적과 투영된 표면적 사이의 비율로 정의됩니다.

표면이 불균일하게 젖어 있으면 액적은 Cassie-Baxter ^[12]상태가 된다.가장 안정적인 접촉각을 영 접촉각에 연결할 수 있습니다.Wenzel과 Cassie-Baxter 방정식에서 계산한 접촉각은 실제 ^[13]표면에서 가장 안정적인 접촉각의 근사치인 것으로 밝혀졌다.

동적 접촉 각도

표면 위를 빠르게 이동하는 액체는 정지 상태에서 접촉각을 변경할 수 있다.전진하는 접촉각은 속도에 따라 증가하고 후퇴하는 접촉각은 감소합니다.정적 접촉각과 동적 접촉각 사이의 불일치는 모세관 숫자에 거의 비례합니다( $Ca$ a{ $displaystyle$ Ca $Ca$ ^[1]

접촉각 곡률

계면 에너지에 기초하여 두 표면 사이의 표면 액체 또는 액체 브릿지의 프로파일은 영-라플라스 ^[1]방정식으로 설명할 수 있다.이 방정식은 3차원 축대칭 조건에 적용 가능하며 매우 비선형적입니다.이는 드롭 $형상$ $f(x,y)$ f $x$ , $)$ 의 $f(x,y)$ 1차 및 2차 도함수의 곱을 포함하는 평균 곡률 항에 기인합니다 $.$

\kappa _{m}=black {1}{2}}{\frac {(1+{f_{x}^{2}}{y}-2f_{x}f_{x}f_{xy}+(1+{f_{y}{2})f_{x}{f_{x}{f}{f}{2}{f_{f}{f}{y}{f_{f}{f}{f}{f}{f}{f}{f}{f}{f}{f}{f}{f}{f}{

적절한 경계 조건과 연계하여 3차원 낙하 형태를 지배하는 이 타원 편미분 방정식을 푸는 것은 복잡하며, 이에 대한 대체 에너지 최소화 접근방식이 일반적으로 채택된다.이 에너지 최소화 ^[14]방법을 사용하여 3차원 세실 및 펜던트 낙하 형태를 성공적으로 예측했습니다.

일반적인 접촉 각도

영상 접촉 각도 장치로부터의 이미지.물방울이 유리에 떨어지며 아래가 반사됩니다.

약 147°의 접촉각을 나타내는 연잎 표면의 물방울.

접촉 각도는 오염에 매우 민감하다. 몇 도 이상 재현 가능한 값은 일반적으로 정제된 액체와 매우 깨끗한 고체 표면이 있는 실험실 조건에서만 얻을 수 있다.액체 분자가 고체 분자에 강하게 끌리면 액체 방울이 고체 표면에 완전히 퍼져 0°의 접촉 각도에 대응합니다.이는 금속 또는 세라믹 ^[15]표면이 없는 물의 경우로, 고체 표면에 산화층이나 오염 물질이 있으면 접촉각이 크게 증가할 수 있습니다.일반적으로 물 접촉각이 90° 미만이면 고체 표면을 친수성^[16], 물 접촉각이 90° 이상이면 고체 표면을 소수성으로 본다.많은 폴리머가 소수성 표면을 나타낸다.낮은 표면 에너지(예: 불소화) 물질로 만들어진 고도 소수성 표면은 θ 120°^[15]의 물 접촉각을 가질 수 있다.표면이 매우 거친 일부 재료는 액체 방울 아래에 에어 포켓이 있기 때문에 물 접촉 각도가 150°를 초과할 수 있습니다.이것들은 초소수성 표면이라고 불립니다.

액체가 아닌 가스를 통해 접촉각을 측정할 경우 180°에서 주어진 값을 뺀 값으로 대체해야 합니다.접촉각은 두 액체의 계면에 동일하게 적용되지만, 논스틱 팬이나 방수 직물 같은 고체 제품에서 더 일반적으로 측정됩니다.

접촉각 제어

습윤 접촉각의 제어는 다양한 유기 및 무기 분자의 표면에 퇴적 또는 혼입함으로써 이루어지는 경우가 많다.이는 종종 SAM(자체 조립식 단분자층) 층을 형성할 수 있는 특수 실란 화학 물질을 사용하여 달성됩니다.다양한 분자구조를 가진 유기분자와 탄화수소 및/또는 과불소화 종단의 양을 적절히 선택함으로써 표면의 접촉각을 조정할 수 있다.이러한 특수 실란은^[17] 특수 진공 오븐 또는 액상 프로세스를 사용하여 기체 단계에서 증착될 수 있습니다.표면에 과불화 종단을 더 많이 결합할 수 있는 분자는 표면 에너지(높은 물 접촉 각도)를 낮출 수 있습니다.

표면 불소가 접촉각에 미치는 영향	물 접촉각
전구체	광택이 나는 실리콘(실리콘) 위에 있습니다.
헤니코실-1,1,2,2-테트라히드로도데실디메틸트리스(디메틸아미노실란)	118.0
헵타데카플루오로-1,1,2,2-테트라히드로데실트리클로로실란– (FDTS)	110.0
노나플루오로-1,1,2,2-테트라히드록실트리스(디메틸아미노)실란	110.0
3, 3, 4, 4, 5, 6, 6-노나플루오로헥실트리클로로실란	108.0
트리데카플루오로-1,1,2,2-테트라히드로옥틸트리클로로실란– (FOTS)	108.0
BIS(트리데카플루오로-1,1,2,2-테트라히드로옥틸)디메틸옥시메틸클로로실란	107.0
도데실트리클로로실란– (DDTS)	105.0
디메틸디클로로실란 – (DDMS)	103.0
10-우데세닐트리클로로실란– (V11)	100.0
펜타플루오로페닐프로필트리클로로실란	90.0

측정 방법

접촉각 고니오미터는 접촉각을 측정하기 위해 사용된다.

동적 세실 드롭 방식

정적 sessile drop 방식

sessile drop contact angle은 고체 기판상의 순수한 액체의 프로파일을 캡처하기 위해 광학 서브시스템을 사용하는 접촉각 고니오미터에 의해 측정됩니다.액체-고체 계면과 액체-증기 계면 사이에 형성되는 각도가 접촉각이다.구형 시스템은 백라이트가 있는 현미경 광학 시스템을 사용했습니다.현재 세대 시스템은 고해상도 카메라와 소프트웨어를 사용하여 접촉 각도를 캡처하고 분석합니다.이러한 방법으로 측정된 각도는 종종 전진하는 접촉 각도에 매우 가깝습니다.평형 접촉각은 잘 정의된 ^[18]진동을 가함으로써 얻을 수 있다.

펜던트 드롭 방법

펜던트 드롭의 접촉각 측정은 반전 드롭의 본질적인 불안정성 때문에 세실 드롭보다 훨씬 복잡하다.이 복잡성은 표면을 기울이려고 할 때 더욱 증폭된다.경사 기판의 펜던트 낙하 접각을 측정하는 실험 장치가 ^[19]최근 개발되었습니다.이 방법을 사용하면 텍스처 기판의 밑면에 여러 마이크로드롭을 증착할 수 있습니다.이러한 마이크로드롭은 고해상도 CCD 카메라로 촬영할 수 있습니다.자동화된 시스템은 기판을 기울이고 전진 및 후퇴하는 접촉각의 계산을 위해 화상을 분석할 수 있도록 한다.

동적 세션 폐기 방식

다이내믹 세션드롭은 스태틱세실드롭과 비슷하지만 드롭을 변경해야 합니다.일반적인 유형의 동적 세실 강하 연구는 볼륨을 동적으로 추가함으로써 고액 계면적을 늘리지 않고 가능한 가장 큰 접촉 각도를 결정합니다.이 최대 각도는 전진 각도입니다.볼륨을 제거하여 가능한 최소 각도인 후퇴 각도를 생성합니다.전진각과 후퇴각의 차이는 접촉각 이력입니다.

다이내믹 윌헬미법

로드/파이버의 동적 접촉 각도 측정.

균일한 지오메트리의 솔리드 상에서 평균 전진 및 후퇴 접각을 산출하는 방법.솔리드의 양쪽은 동일한 속성을 가져야 합니다.고체가 알려진 표면 장력의 액체에 침지되거나 액체에서 빠져 나올 때 고체에 대한 습윤력이 측정됩니다.이 경우 매우 제어된 진동을 가함으로써 평형 접촉각을 측정할 수 있다.VIECA라고 불리는 이 방법론은 모든 윌헬미 ^[20]균형에서 매우 간단한 방법으로 구현될 수 있습니다.

단섬유 윌헬미법

단섬유에 적용되는 다이내믹 윌헬미법.진각 및 후퇴각도 측정.

단섬유 메니스커스 접촉각 측정.

단섬유 메니스커스법

단섬유 Wilhelmy 방법의 광학적 변화.저울로 측정하는 것이 아니라 고해상도 카메라로 파이버상의 메니스커스 형상을 직접 촬영한다.그런 다음 자동 메니스커스 형상 피팅을 통해 파이버의 정적, 전진 또는 후퇴하는 접촉 각도를 직접 측정할 수 있습니다.

와슈번 방정식 모세관 상승법

다공질 재료의 경우 계산된 세공 직경의 물리적 의미와 이 방정식을 고체의 접촉각 계산에 사용할 수 있는 실제 가능성에 대해 많은 문제가 제기되어 왔습니다. 이 방법은 많은 소프트웨어에서 ^[21]^{[clarification needed]}통합적으로 제공되고 있습니다.시간의 함수로서의 무게의 변화를 측정한다.^[22]

「」를 참조해 주세요.

레퍼런스

^ ^a ^b ^c ^d Shi, Z.; et al. (2018). "Dynamic contact angle hysteresis in liquid bridges". Colloids and Surfaces A: Physicochemical and Engineering Aspects. 555: 365–371. arXiv:1712.04703. doi:10.1016/j.colsurfa.2018.07.004. S2CID 51916594.
^ "III. An essay on the cohesion of fluids". Philosophical Transactions of the Royal Society of London. 95: 65–87. January 1805. doi:10.1098/rstl.1805.0005. ISSN 0261-0523. S2CID 116124581.
^ Gibbs, J. Willard (Josiah Willard) (1961). Scientific papers. Dover Publications. ISBN 978-0486607214. OCLC 964884.
^ ^a ^b ^c Jasper, Warren J.; Anand, Nadish (May 2019). "A generalized variational approach for predicting contact angles of sessile nano-droplets on both flat and curved surfaces". Journal of Molecular Liquids. 281: 196–203. doi:10.1016/j.molliq.2019.02.039. ISSN 0167-7322. S2CID 104412970.
^ Jasper, Warren J.; Rasipuram, Srinivasan (December 2017). "Relationship between contact angle and contact line radius for micro to atto [10−6 to 10−18] liter size oil droplets". Journal of Molecular Liquids. 248: 920–926. doi:10.1016/j.molliq.2017.10.134. ISSN 0167-7322.
^ Hattori, Tsuyoshi; Koshizuka, Seiichi (2019). "Numerical simulation of droplet behavior on an inclined plate using the Moving Particle Semi-implicit method". Mechanical Engineering Journal. 6 (5): 19-00204–19-00204. doi:10.1299/mej.19-00204. ISSN 2187-9745.
^ Tadmor, Rafael (2004). "Line energy and the relation between advancing, receding, and Young contact angles". Langmuir. 20 (18): 7659–64. doi:10.1021/la049410h. PMID 15323516.
^ Chibowski, Emil (2008). "Surface free energy of sulfur—Revisited I. Yellow and orange samples solidified against glass surface". Journal of Colloid and Interface Science. 319 (2): 505–13. Bibcode:2008JCIS..319..505C. doi:10.1016/j.jcis.2007.10.059. PMID 18177886.
^ de Gennes, P.G. (1985). "Wetting: statics and dynamics". Reviews of Modern Physics. 57 (3): 827–863. Bibcode:1985RvMP...57..827D. doi:10.1103/RevModPhys.57.827.
^ "Influence of surface roughness on contact angle and wettability" (PDF).
^ Wenzel, Robert N. (1936-08-01). "Resistance of Solid Surfaces to Wetting by Water". Industrial & Engineering Chemistry. 28 (8): 988–994. doi:10.1021/ie50320a024. ISSN 0019-7866.
^ Cassie, A. B. D.; Baxter, S. (1944-01-01). "Wettability of porous surfaces". Transactions of the Faraday Society. 40: 546. doi:10.1039/tf9444000546. ISSN 0014-7672.
^ Marmur, Abraham (2009-07-06). "Solid-Surface Characterization by Wetting". Annual Review of Materials Research. 39 (1): 473–489. Bibcode:2009AnRMS..39..473M. doi:10.1146/annurev.matsci.38.060407.132425. ISSN 1531-7331.
^ Chen Y, He B, Lee J, Patankar NA (2005). "Anisotropy in the wetting of rough surfaces" (PDF). Journal of Colloid and Interface Science. 281 (2): 458–464. Bibcode:2005JCIS..281..458C. doi:10.1016/j.jcis.2004.07.038. PMID 15571703. Archived from the original (PDF) on 2017-08-10. Retrieved 2017-03-31.{{cite journal}}: CS1 maint: 작성자 파라미터 사용(링크)
^ ^a ^b Zisman, W.A. (1964). F. Fowkes (ed.). Contact Angle, Wettability, and Adhesion. ACS. pp. 1–51.
^ Renate Förch; Holger Schönherr; A. Tobias A. Jenkins (2009). Surface design: applications in bioscience and nanotechnology. Wiley-VCH. p. 471. ISBN 978-3-527-40789-7.
^ Kobrin, B.; Zhang, T.; Chinn, J. "Choice of precursors in Vapor-phase Surface Modification". 209th Electrochemical Society meeting, May 7–12, 2006, Denver, CO.
^ Volpe, C. D.; Brugnara, M.; Maniglio, D.; Siboni, S.; Wangdu, T. (2006). "About the possibility of experimentally measuring an equilibrium contact angle and its theoretical and practical consequences". Contact Angle, Wettability and Adhesion. 4: 79–100.
^ Bhutani, Gaurav; Muralidhar, K.; Khandekar, Sameer (2013). "Determination of apparent contact angle and shape of a static pendant drop on a physically textured inclined surface". Interfacial Phenomena and Heat Transfer. 1: 29–49. doi:10.1615/InterfacPhenomHeatTransfer.2013007038.
^ Volpe, C. D.; Maniglio, D.; Siboni, S.; Morra, M. (2001). "An experimental procedure to obtain the equilibrium contact angle from the Wilhelmy method" (PDF). Oil and Gas Science and Technology. 56: 9–22. doi:10.2516/ogst:2001002.
^ Marco, Brugnara; Claudio, Della Volpe; Stefano, Siboni (2006). "Wettability of porous materials. II. Can we obtain the contact angle from the Washburn equation?". In Mittal, K. L. (ed.). Contact Angle, Wettability and Adhesion. Mass. VSP.
^ Washburn, Edward W. (1921). "The Dynamics of Capillary Flow". Physical Review. 17 (3): 273. Bibcode:1921PhRv...17..273W. doi:10.1103/PhysRev.17.273.

추가 정보

Pierre-Gilles de Genne, Franceoise Brochard-Wyart, David Quéré, 캐필러시티 및 습윤 현상: 낙하, 거품, 진주, 파도, 스프링거(2004)
Jacob Israelachvili, 분자간 및 표면력, 학술언론(1985-2004)
D.W. Van Krevelen, 폴리머의 특성, 제2차 개정판, 암스테르담-옥스포드-뉴욕 엘세비어 사이언티픽 출판사(1976년)
Yuan, Yuehua; Lee, T. Randall (2013). "Contact Angle and Wetting Properties". Surface Science Techniques. Springer Series in Surface Sciences. Vol. 51. doi:10.1007/978-3-642-34243-1. ISBN 978-3-642-34242-4. ISSN 0931-5195. S2CID 137147527.
Clegg, Carl Contact Angle Made Easy, Ramé-hart (2013), ISBN 978-1-300-66298-3

[CAH-1] Shi, Z.; et al. (2018). "Dynamic contact angle hysteresis in liquid bridges". Colloids and Surfaces A: Physicochemical and Engineering Aspects. 555: 365–371. arXiv:1712.04703. doi:10.1016/j.colsurfa.2018.07.004. S2CID 51916594.

[2] "III. An essay on the cohesion of fluids". Philosophical Transactions of the Royal Society of London. 95: 65–87. January 1805. doi:10.1098/rstl.1805.0005. ISSN 0261-0523. S2CID 116124581.

[3] Gibbs, J. Willard (Josiah Willard) (1961). Scientific papers. Dover Publications. ISBN 978-0486607214. OCLC 964884.

[Jasper_196–203-4] Jasper, Warren J.; Anand, Nadish (May 2019). "A generalized variational approach for predicting contact angles of sessile nano-droplets on both flat and curved surfaces". Journal of Molecular Liquids. 281: 196–203. doi:10.1016/j.molliq.2019.02.039. ISSN 0167-7322. S2CID 104412970.

[5] Jasper, Warren J.; Rasipuram, Srinivasan (December 2017). "Relationship between contact angle and contact line radius for micro to atto [10−6 to 10−18] liter size oil droplets". Journal of Molecular Liquids. 248: 920–926. doi:10.1016/j.molliq.2017.10.134. ISSN 0167-7322.

[HATTORIKOSHIZUKA2019-6] Hattori, Tsuyoshi; Koshizuka, Seiichi (2019). "Numerical simulation of droplet behavior on an inclined plate using the Moving Particle Semi-implicit method". Mechanical Engineering Journal. 6 (5): 19-00204–19-00204. doi:10.1299/mej.19-00204. ISSN 2187-9745.

[Tadm-7] Tadmor, Rafael (2004). "Line energy and the relation between advancing, receding, and Young contact angles". Langmuir. 20 (18): 7659–64. doi:10.1021/la049410h. PMID 15323516.

[Chib-8] Chibowski, Emil (2008). "Surface free energy of sulfur—Revisited I. Yellow and orange samples solidified against glass surface". Journal of Colloid and Interface Science. 319 (2): 505–13. Bibcode:2008JCIS..319..505C. doi:10.1016/j.jcis.2007.10.059. PMID 18177886.

[deGennes-9] Gennes, P.G. (1985). "Wetting: statics and dynamics". Reviews of Modern Physics. 57 (3): 827–863. Bibcode:1985RvMP...57..827D. doi:10.1103/RevModPhys.57.827.

[10] "Influence of surface roughness on contact angle and wettability" (PDF).

[11] Wenzel, Robert N. (1936-08-01). "Resistance of Solid Surfaces to Wetting by Water". Industrial & Engineering Chemistry. 28 (8): 988–994. doi:10.1021/ie50320a024. ISSN 0019-7866.

[12] Cassie, A. B. D.; Baxter, S. (1944-01-01). "Wettability of porous surfaces". Transactions of the Faraday Society. 40: 546. doi:10.1039/tf9444000546. ISSN 0014-7672.

[13] Marmur, Abraham (2009-07-06). "Solid-Surface Characterization by Wetting". Annual Review of Materials Research. 39 (1): 473–489. Bibcode:2009AnRMS..39..473M. doi:10.1146/annurev.matsci.38.060407.132425. ISSN 1531-7331.

[14] Chen Y, He B, Lee J, Patankar NA (2005). "Anisotropy in the wetting of rough surfaces" (PDF). Journal of Colloid and Interface Science. 281 (2): 458–464. Bibcode:2005JCIS..281..458C. doi:10.1016/j.jcis.2004.07.038. PMID 15571703. Archived from the original (PDF) on 2017-08-10. Retrieved 2017-03-31.{{cite journal}}: CS1 maint: 작성자 파라미터 사용(링크)

[zisman-15] Zisman, W.A. (1964). F. Fowkes (ed.). Contact Angle, Wettability, and Adhesion. ACS. pp. 1–51.

[16] Renate Förch; Holger Schönherr; A. Tobias A. Jenkins (2009). Surface design: applications in bioscience and nanotechnology. Wiley-VCH. p. 471. ISBN 978-3-527-40789-7.

[17] Kobrin, B.; Zhang, T.; Chinn, J. "Choice of precursors in Vapor-phase Surface Modification". 209th Electrochemical Society meeting, May 7–12, 2006, Denver, CO.

[18] Volpe, C. D.; Brugnara, M.; Maniglio, D.; Siboni, S.; Wangdu, T. (2006). "About the possibility of experimentally measuring an equilibrium contact angle and its theoretical and practical consequences". Contact Angle, Wettability and Adhesion. 4: 79–100.

[bhutani-19] Bhutani, Gaurav; Muralidhar, K.; Khandekar, Sameer (2013). "Determination of apparent contact angle and shape of a static pendant drop on a physically textured inclined surface". Interfacial Phenomena and Heat Transfer. 1: 29–49. doi:10.1615/InterfacPhenomHeatTransfer.2013007038.

[20] Volpe, C. D.; Maniglio, D.; Siboni, S.; Morra, M. (2001). "An experimental procedure to obtain the equilibrium contact angle from the Wilhelmy method" (PDF). Oil and Gas Science and Technology. 56: 9–22. doi:10.2516/ogst:2001002.

[Brugnara-21] Marco, Brugnara; Claudio, Della Volpe; Stefano, Siboni (2006). "Wettability of porous materials. II. Can we obtain the contact angle from the Washburn equation?". In Mittal, K. L. (ed.). Contact Angle, Wettability and Adhesion. Mass. VSP.

[washburn-22] Washburn, Edward W. (1921). "The Dynamics of Capillary Flow". Physical Review. 17 (3): 273. Bibcode:1921PhRv...17..273W. doi:10.1103/PhysRev.17.273.

[1]

[2]

[3]

[4]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

Search

접촉각

네임스페이스

더

목차