아이솔린 검색

Isoline recovery는 원거리 감지 역법으로서, 대기권 구성 요소 또는 변수의 아이솔린을 하나 이상 회수한다.다른 윤곽선의 유효성을 확인하는 데 사용할 경우 작업에 대해 가능한 가장 정확한 방법이다.전체 필드를 검색하는 데 사용할 경우 일반적이고 비선형적인 역법이며 견실한 추정기가 된다.

첨부된 윤곽선의 유효성을 확인하는 경우

이론적 근거

등고선 연결에서와 같이 대기 구성 요소의 단일 등고선 또는 아이솔린에 대한 추론된 지식을 가지고 있으며, q 위성 원격 감지 데이터에 대해 이를 검증하고자 한다고 가정합시다.위성 기기는 구성 요소를 직접 측정할 수 없기 때문에 우리는 일종의 역전을 수행해야 한다.등고선의 유효성을 확인하기 위해 어떤 특정 지점에서 구성 요소의 정확한 값을 알 필요는 없다.우리는 그것이 내부인지 외부인지, 즉 등고선의 값보다 큰지 아니면 작은지 알기만 하면 된다, q₀.

이것은 분류 문제다.허용:

${\displaystyle j={\prease}1;&q<q_{0}\\2;&q\geq q_{0}\end{case}}}}}$

변수가 되다이는 위성 측정 벡터,${\displaystyle \stackrel{}{}}y{\displaystyle \stackrel{}{}}$ → ${\$${\displaystyle vec}$${y$ 어떤 조건부 확률에 의해 $P{\displaystyle (y\stackrel{}{}}$→ j${\displaystyle )}$ ${\displaystyle P({\vec {y}j)}$와 관련될 것이며$,$ 우리는 측정 벡터와 상태 변수 q.를 생성하여 교육 데이터라 불리는 표본을 수집함으로써 근사하게 된다.관심 영역에 대한 이온 결과 및 두 클래스를 분리하기 위해 어떤 윤곽 알고리즘을 사용하든, 아이솔린은 "상호"가 될 것이다.

검색의 정확성은 관심 영역에 대한 조건부 확률을 통합함으로써 제공될 것이다. A:

${\displaystyle a={\frac {1}{A}}\int _{A}P\left[c({\vec{r}}) {\vec}{y}}({\vec{r}})\,d{\vec {r}}}$

여기서 c는 $위치$에서 검색된 클래스, r${\displaystyle \stackrel{}{}}$→ ${\$ 각 지점에서 통합의 가치를 극대화하여 이 양을 최대화할 수 있다.

${\displaystyle \max(a)={\frac {1}{A}}\int _{A}\left\lbrace \max _{j}P\left[j {\bec {y}}({\vec{r}})\right]\rbrace \d{\vec {r}}}$

이것은 최대우도의 정의이므로 최대우도에 기초한 분류 알고리즘은 부가된 윤곽선의 유효성을 검증할 수 있는 가장 정확한 방법이다.훈련 데이터 집합에서 최대우도 분류를 수행하는 좋은 방법은 가변 커널 밀도 추정이다.

교육자료

교육 데이터를 생성하는 방법에는 두 가지가 있다.가장 분명한 것은 단순히 변수의 측정치인 q를 위성 계측기의 조합된 측정치와 일치시킴으로써 경험적으로 명백하다.이 경우, 측정을 생성하는 실제 물리학에 대한 지식이 필요하지 않으며, 검색 알고리즘은 순수하게 통계적이다.두 번째는 전진 모델:

${\displaystyle {\vec{y}={\vec {f}({\vec {x}})\,}$

여기서 $x{\displaystyle \stackrel{}{}}$→ ${\$은(는) 상태 벡터, q_k = x는 단일 구성 요소다.이 방법의 장점은 상태 벡터가 실제 대기 구성을 반영할 필요가 없고 실제 대기에서 합리적으로 발생할 수 있는 상태만 차지하면 된다는 것이다.또한 쌍체 샘플 위치의 오프셋 오류와 두 계측기의 설치 공간 크기 차이로 인해 대부분의 데이터 정렬 절차에서 내재된 오류는 없다.그러나, 재발견은 더 흔한 주들에 편중될 것이기 때문에, 통계는 현실 세계의 주들을 반영해야 한다.

오류 특성화

조건부 확률인 $P{\displaystyle (y\stackrel{}{}}$→${\displaystyle j}$ $){\displaystyle P({\vec{y}j$는 오류 특성화가 우수하므로 분류 알고리즘은 이를 반환해야 한다.조건부 확률을 재조정하여 신뢰 등급을 정의한다.

${\displaystyle C={\frac {n_{c}P(c {\vec {y})-1}{n_{c}-1}$

여기서 n은_c 클래스 수입니다(이 경우, 2).C가 0이면 우연한 점보다 분류가 조금 나은 반면, 하나면 완벽해야 한다.신뢰도를 통계적 허용오차로 변환하기 위해 진정한 아이솔린을 알 수 있는 아이솔린 검색에 다음과 같은 라인 적분을 적용할 수 있다.

${\displaystyle \delta (C)={\frac {1}{l}\int _{0}^{l}h(C-C^{\vec {r})\,ds}$

여기서 s는 경로, l는 아이솔린의 길이, $C{\displaystyle {}^{}}$ $′{\$는 위치 함수로서 회수된 자신감이다$$.신뢰도 C의 각 값에 대해 적분을 별도로 평가해야 하는 것으로 보이지만, 사실 $결과$의 신뢰도 C$′{\$을(를) 정렬하여 C의 모든 값에 대해 수행할 수 있다$.$함수는 공차가 적용되는 신뢰 등급의 임계값과 관련된다.즉, 허용오차와 동일한 실제 아이솔린의 일부분을 포함하는 영역을 정의한다.

예: AMSU에서 나오는 수증기

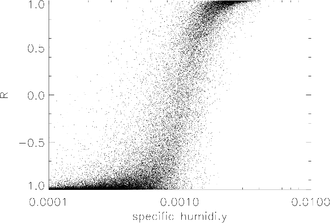
AMSU(Advanced Microweet Sounding Unit) 시리즈 위성 기기는 온도 및 수증기를 감지하도록 설계되었다.이들은 수평 해상도가 높은(15km에 불과하며, 위성 1개 이상에 탑재되기 때문에 하루도 안 돼 전지구적 커버리지를 완전하게 얻을 수 있다.훈련 데이터는 RTTOV라는 고속 복사 전송 모델에 공급된 유럽 중거리 기상 예측 센터(ECMWF) 평균자책 40 데이터를 사용하여 생성되었다.함수 $\Delta {\displaystyle }$(${\displaystyle C}$) ${\displaystyle \delta (C)}$는 시뮬레이션된 검색에서 생성되었으며$$ 오른쪽 그림에 표시된다.그런 다음 0.8 미만의 모든 신뢰 등급을 음영 처리하여 아래 그림의 90% 공차를 설정하는 데 사용한다.따라서 우리는 진정한 아이솔린이 90%의 음영 안에 들어갈 것으로 예상한다.

연속 검색용

아이솔린 검색은 연속체 변수를 검색하는 데도 유용하며 일반적인 비선형 역법을 구성한다.국소적 최소치에서 고착될 가능성이 없다는 점에서 전방 모델을 직접 뒤집는 최적 추정 등 반복적 방법뿐 아니라 신경망 양쪽 모두에 비해 이점이 있다.

탈원형 변수의 연속형 변수를 재구성하는 방법에는 여러 가지가 있다.일단 충분한 수의 윤곽선이 검색되면, 그들 사이에 보간하는 것이 간단하다.조건부 확률은 연속체 값의 좋은 대용물이 된다.

연속체에서 이산형 변수로의 변환을 고려해 보십시오.

${\displaystyle P(1 {\vec {y})=\int_{-\infit }^{q_{0}P(q {\vec {y}})\,dq}$

${\displaystyle P(2 {\vec {y})=\int _{q_{0}^{\infit }P(q {\vec {y})\,dq}$

$P{\displaystyle }$(${\displaystyle qy\stackrel{}{}}$→${\displaystyle }$) ${\displaystyle P(q {\vec$ {y$}})$가 가우스인에 의해 주어진다고 가정하자$$.

${\displaystyle P(q {\vec {y}})={\frac {1}{{\sqrt {2\pi }}\sigma _{q}}}\exp \left\lbrace -{\frac {\left[q-{\bar {q}}({\vec {y}})\right]^{2}}{2\sigma _{q}}}\right\rbrace }$

여기서 $'{\$은 기대값이고 $\sigma {\displaystyle {}_{}}$ ${\displaystyle q_{}}$ ${\$ \$ma_{q}은$표준 편차인 경우$$ 조건부 확률은 오차 함수에 의해 연속 변수 q와 관련된다.

${\displaystyle R=P(2 {\vec {y}})-P(1 {\vec {y})=\mathrm {erf}\lef[{\frac {q_{0}-{\bar{q}}({\vec {y}})}{\sqrt{2}}\sigma _}\rigma}\rigma}\rigma]}}}}}}}}$

그림에는 위에서 설명한 예시 검색에 대한 조건부 확률 대 특정 습도가 표시된다.

견실한 추정자로서

q의₀ 위치는 다음과 같은 두 등급의 조건부 확률을 동일하게 설정함으로써 찾을 수 있다.

${\displaystyle \int _{-\infit _}^{q_{0}P(q {\vec {y}})\,dq=\int _{0}^{0}}{\infit }P(q {\vec {y}})\,dq}$

즉, 같은 양의 "제로오더 모멘트"가 q의₀ 양쪽에 놓여 있다.이러한 유형의 제형은 견실한 추정기의 특징이다.

참조

• Peter Mills (2009). "Isoline retrieval: An optimal method for validation of advected contours" (PDF). Computers & Geosciences. 35 (11): 2020–2031. arXiv:1202.5659. Bibcode:2009CG.....35.2020M. doi:10.1016/j.cageo.2008.12.015.

• Peter Mills (2010). "Efficient statistical classification of satellite measurements" (PDF). International Journal of Remote Sensing. arXiv:1202.2194. doi:10.1080/01431161.2010.507795. Archived from the original (PDF) on 2012-04-26. Retrieved 2011-12-28.

외부 링크

• 아이솔린 검색용 소프트웨어