아이소퀀트
Isoquant미시경제학에서 icoquant(수량과 그리스어 ico, 등가)는 두 개 이상의 입력량을 변경하면서 동일한 양의 출력이 생성되는 점 집합을 통해 그려진 등고선이다.[1][2] 등분류의 x축과 y축은 통상 노동, 자본, 토지 또는 조직과 같은 생산 요소인 두 개의 관련 입력물을 나타낸다. 이소 분량은 "Iso-Product Curve" 또는 "Equal Product Curve"로도 알려져 있다.
이소쿼런트 vs. 무관심 곡선
무관심 곡선 매핑은 소비자의 효용 극대화 문제를 해결하는 데 도움이 되지만, 이소쿼터 매핑은 생산자의 비용 최소화 및 수익과 생산량 극대화 문제를 다룬다. 무관심 곡선은 효용에 대한 정확한 측정을 제공할 수 없다는 점에서 등사분기에는 기준선과 관련된 방법만이 기준선과 관련이 있다. 반면, 등분자에서 제품은 물리적 단위로 정확하게 측정할 수 있으며, 등분 1이 등분 2를 얼마나 초과하는지 정확히 알 수 있다.
Isoquant의 특성과 실용성
경영경제학에서 이소쿼터는 일반적으로 자본-노동 그래프에서 이소코스트 곡선과 함께 그려지며, 생산함수에서 자본과 노동 사이의 기술적 절충과 두 투입변수의 한계수익의 감소를 보여준다. 경영경제학에서 이소 퀀트의 단위는 일반적으로 자본비용의 순액이다. 이와 같이 기술대체율(MRTS)이 감소하는 가동으로 인해 본질적으로 이소쿼터는 하향경사한다.[3][4] 등분류의 경사는 입력 x를 입력 y로 대체할 수 있는 속도를 나타낸다.[5] 이 개념은 MRTS이기 때문에 MRTS=isoquant의 슬로프. 따라서, 등분율이 높을수록 MRTS는 더 높다. MRTS는 감소해야 하기 때문에, 등가물은 그 기원과 볼록해야 한다. 다른 상수를 잡으면서 한 입력을 추가하면 결국 한계 출력이 감소한다.
등분류의 등고선은 기업의 자원 사용(예산과 같은 시간)을 완전히 최대화하는 두 가지 입력물의 모든 조합을 나타낸다. 자원의 완전한 극대화는 보통 '효율적'으로 간주된다. 생산 인자의 효율적인 배분은 두 개의 등분자가 서로 접하는 경우에만 발생한다. 만약 기업이 등고선 왼쪽에서 생산한다면, 그 회사는 그들의 가용 자원의 사용을 극대화하는 것이 아니기 때문에 비효율적으로 운영되고 있는 것으로 간주된다.[6] 기업은 제약조건을 초과하지 않는 한 등고선 오른쪽에서 생산할 수 없다.
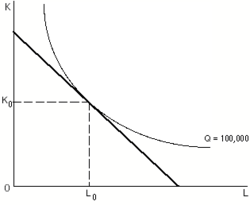
등분자 집단은 각각 다른 양의 출력을 나타내는 여러 등분자를 결합한 그래프인 등분자 지도로 나타낼 수 있다.등분율 지도는 출력이 증가함에 따라 고정 출력 증가의 등분율 쌍 사이의 증가 또는 감소 거리를 기반으로 하는 척도로의 수익률 감소 또는 증가를 나타낼 수 있다.[7] 출력이 증가함에 따라 그러한 등분사 사이의 거리가 증가하면, 회사의 생산기능은 규모에 대한 수익률이 감소하는 것을 보여주고 있다. 두 입력을 두 배로 늘리면 이전 등분사 출력의 두 배가 되지 않는 등분사에 배치될 것이다. 반대로, 출력이 증가함에 따라 거리가 감소하는 경우, 기업은 규모에 대한 수익률을 증가시키고 있다. 두 입력을 두 배로 증가시키면 원래 아이소쿼런트의 출력이 두 배 이상 되는 아이소쿼런트에 배치된다. 기업은 자원을 배분하는 방법을 통찰력 있게 사용함으로써, 아이소퀀트가 규모에 맞게 수익률에 주는 정보를 활용하도록 선택할 수 있다.[8]
자원을 배분하는 방법을 아는 것은 경영경제학과 관련된 개념이다. 등가물은 이 희소성 문제를 그래픽으로 표현하는데 유용할 수 있다. 그들은 동일한 수준의 출력을 생산하기 위해 해당 기업이 두 개의 다른 입력(그래프의 x와 y)을 마음대로 대체할 수 있는 능력을 가지고 있는 정도를 보여준다(그래프 C 참조). 그것들은 또한 예산 제약에 따르는 두 상품의 다른 수량 조합을 나타낸다. 따라서, 그것들은 비용이나 폐기물 최소화, 수익과 산출물의 극대화와 같은 생산과 이익 딜레마에 관한 경영진의 더 나은 정보에 입각한 의사결정을 돕는 도구로 사용될 수 있다.
기업은 이소코스트 곡선과 이소쿼터를 결합하고 최초 주문 조건을 준수함으로써 주어진 출력을 생산하기 위한 입력물의 최소 비용 조합을 결정할 수 있다.[3] 최소 비용 조합은 한계 상품의 비율이 요인 가격의 비율과 동일한 경우다. 이 지점에서 등분체의 기울기와 등고스트의 기울기가 같을 것이다(그래프 D의 교차점 참조). 기업은 적어도 원가 조합을 생산할 동기를 가지고 있다. 왜냐하면 이 시점에서 원하는 생산의 관련 원가는 최소화되기 때문이다.[9]
무관심 곡선과 마찬가지로 두 개의 등가물은 절대 건널 수 없다. 또한 입력의 가능한 모든 조합은 등분류에 있다. 마지막으로, 등분율 결과의 위 또는 오른쪽에 있는 입력의 조합은 더 높은 수준의 출력을 나타내며, 그 반대의 경우도 마찬가지다. 입력의 한계 생산물은 다른 모든 입력물을 일정하게 유지하면서 입력의 양을 증가시키면서 감소하지만, 한계 생산물은 합리적 기업이 출력을 감소시키기 위해 입력량을 증가시키지 않기 때문에 경험적으로 관찰된 범위에서 결코 음수가 아니다.
Isoquant의 모양
만약 두 입력이 완벽한 대체물이라면, 생성된 결과로 생성된 이소 퀀트 맵은 무화과로 표시된다. A; 주어진 생산 Q3 수준으로, 입력 X는 불변의 속도로 입력 Y로 대체될 수 있다. 완벽한 대체 투입변수는 생산기능에서 서로 대체할 때 한계 수익률이 감소하는 것을 경험하지 않는다.
만약 두 입력이 완벽한 보완이라면, 이소 퀀트 맵은 무화과 형태를 취한다. B; 생산 Q3 수준의 경우, 입력 X와 입력 Y는 등분류의 꼬임에서 발생하는 특정 비율에서만 효율적으로 결합될 수 있다. 회사는 이윤을 극대화하기 위해 필요한 비율의 두 투입물을 결합할 것이다.
주어진 출력 수준에 대한 비용 최소화 문제를 해결하기 위해 일반적으로 이소쿼터를 이소코스트 라인과 결합된다. 상단 그림에 표시된 일반적인 사례에서, 매끄럽게 곡선을 이루는 등고스트 입력을 가진 단가가 고정된 기업은 선형 및 하향 경사인 등고스트 곡선을 가질 것이다. 등고스트 곡선과 등고스트 곡선 사이의 모든 접점은 i와 관련된 출력 레벨을 생산하기 위한 비용 최소화 입력 조합을 나타낸다.소량의 (입력가격이 일정하게 유지되는) 등쿼터와 이소코스트의 접선점을 연결하는 선을 확장 경로라고 한다.[10]
비대류
기술적 대체의 한계율 감소와 따라서 대체의 양의 유한한 탄성을 가정할 때, 등분류는 원점에 볼록하다. 입력 중 하나를 스케일링할 수 있을 정도로 강한 수익률이 있는 경우 국소적으로 비콘벡스 등분자가 발생할 수 있다. 이 경우 대체에 부정적인 탄성이 있다 - 입력 A 대 입력 B의 비율이 증가함에 따라 B에 대한 A의 한계 생산물은 감소하기보다는 증가한다.
비컨벡스 등분류는 가격변동에 대응하여 입력 혼합을 최소화하는 가격에 크고 불연속적인 변화를 발생시키기 쉽다. 예를 들어, isoquant가 전체적으로 비콘벡스이고 Isocost 곡선이 선형인 경우를 생각해 보자. 이 경우 입력값의 최소 비용 혼합은 코너 솔루션이 될 것이며, 입력 A 또는 입력 B 중 하나만 포함한다. 사용할 입력의 선택은 상대 가격에 따라 달라진다. 일부 임계 가격비에서, 최적 입력 혼합은 상대 가격의 작은 변화에 대응하여 모든 입력 A에서 모든 입력 B로 이동하며, 그 반대의 경우도 마찬가지다.
참고 항목
| 위키미디어 커먼즈에는 아이소쿼터와 관련된 미디어가 있다. |
참조
- ^ Varian, Hal R. (1992). Microeconomic Analysis (Third ed.). Norton. ISBN 0-393-95735-7.
- ^ Chiang, Alpha C. (1984). Fundamental Methods of Mathematical Economics (Third ed.). McGraw-Hill. pp. 359–363. ISBN 0-07-010813-7.
- ^ a b www2.econ.iastate.edu http://www2.econ.iastate.edu/classes/econ101/choi/ch11d.htm. Retrieved 2021-04-25. 누락 또는 비어 있음
title=(도움말) - ^ "Isoquants". www.economics.utoronto.ca. Retrieved 2021-04-25.
- ^ "Production Functions" (PDF). UCLA. n.d. Retrieved 25 April 2021.
- ^ Arrow, K. J.; Chenery, H. B.; Minhas, B. S.; Solow, R. M. (1961). "Capital-Labor Substitution and Economic Efficiency". The Review of Economics and Statistics. 43 (3): 225–250. doi:10.2307/1927286. ISSN 0034-6535. JSTOR 1927286.
- ^ Kwatiah, Natasha (2016-03-02). "The Laws of Returns to Scale in Terms of Isoquant Approach". Economics Discussion. Retrieved 2021-04-25.
- ^ "The Discovery of the Isoquant". ResearchGate. Retrieved 2021-04-25.
- ^ "Expansion path, ridgeline and least cost combination of inputs" (PDF). Eagri. n.d. Retrieved 2021-04-25.
- ^ 살바토레, 도미니크(1989년). Schaum의 경영경제학 이론과 문제 개요 McGraw-Hill, ISBN 978-00-07-054513-7






