트리 분해

Tree decomposition
이 기사는 그래프의 트리 구조에 관한 것입니다.그래프를 트리로 분해하는 방법은 그래프 이론 decomp 분해 문제를 참조하십시오.자연 상태의 트리 분해에 대해서는 간호사 로그를 참조하십시오.
8개의 정점이 있는 그래프와 6개의 노드가 있는 트리로의 트리 분해.각 그래프 엣지는 어떤 트리 노드에서 함께 나열된 두 개의 정점을 연결하고 각 그래프 정점은 트리의 연속된 하위 트리의 노드에 나열됩니다.각 트리 노드는 최대 3개의 정점을 나열하므로 이 분해의 폭은 2개입니다.

그래프 이론에서, 트리 분해는 그래프의 나무 폭을 정의하고 그래프 상의 특정 계산 문제를 해결하는 데 사용될 수 있는 트리에 대한 그래프 매핑입니다.

트리 분해는 결합 트리, 패거리 트리 또는 결합 트리라고도 불리며 확률론적 추론, 제약 조건 만족도, 쿼리 최적화 [citation needed]및 매트릭스 분해와 같은 문제에 중요한 역할을 한다.

나무 분해의 개념은 원래 루돌프 할린(1976)에 의해 도입되었다.나중에 그것은 닐 로버트슨과 폴 시모어에 의해 재발견되었고 그 이후로 많은 다른 [1]작가들에 의해 연구되었다.

정의.

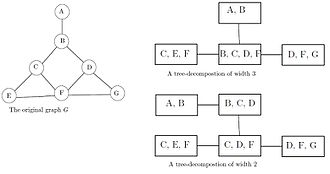
직관적으로, 트리 분해는 대응하는 서브트리가 교차할 때만 해당 그래프 내의 정점이 인접하도록 주어진 그래프 G의 정점을 트리의 서브트리로 나타낸다.따라서 G는 하위 트리의 교차 그래프의 하위 그래프를 형성한다.전체 교차 그래프는 화음 그래프입니다.

각 서브트리는 그래프 정점과 트리 노드 세트를 관련짓습니다.이를 공식적으로 정의하기 위해 각 트리 노드를 연관된 정점 집합으로 나타냅니다.따라서 그래프 G = (V, E)가 주어졌을 때, 트리 분해는 쌍(X, T)이며, 여기서 X = {X1n, …, X}는 V의 부분 집합(때로는 가방이라고 함) 패밀리이고, T는 노드가 부분 집합i X인 트리이며, 다음과 같은 특성을 [2]만족합니다.

  1. 모든 집합i X의 합계는 V와 같다.즉, 각 그래프 정점은 하나 이상의 트리 노드와 연결됩니다.
  2. 그래프의 모든 에지(v, w)에 대해 v와 w를 모두 포함하는 부분 집합i X가 있습니다.즉, 대응하는 서브트리에 공통 노드가 있는 경우에만 그래프에 정점이 인접해 있습니다.
  3. X와j X가 모두 정점 v를 포함하는 경우i X와 Xj 사이의i (고유한) 경로에 있는 트리의 모든 노드k X도 v를 포함합니다.즉, 정점 v와 관련된 노드는 T의 연결된 서브셋을 형성합니다.이를 일관성 또는 실행 교차로 속성이라고도 합니다.X, Xj 및k X가 노드이고k X가 X에서X로의ij 경로 상에 있는 경우i i k\ X _ { } \ X _ { j } \ { k

그래프의 트리 분해는 고유하지 않습니다. 예를 들어 사소한 트리 분해는 그래프의 모든 정점을 단일 루트 노드에 포함합니다.

기본 트리가 경로 그래프인 트리 분해를 경로 분해라고 하며, 이러한 특수한 트리 분해 유형에서 도출된 폭 파라미터를 경로 폭이라고 한다.

트리 k의 트리 분해(X, T = (I, F)는 모든 i I: + (\i: +1이고 iF : j kstyle ( )의 경우 매끄럽다.

트리 분해의 최소 트리 수는 G의 트리 수입니다.

트리 폭

주요 기사:트리 폭
동일한 그래프의 서로 다른 두 트리 구성

트리 분해의 폭은 가장 큰 집합i X에서 1을 뺀 크기입니다.그래프 G의 트리 폭 tw(G)는 G의 가능한 트리 분해 중 최소 폭이다.이 정의에서는 트리의 트리 폭을 1과 같게 하기 위해 가장 큰 집합의 크기가 1만큼 감소합니다.트리 폭은 화음 그래프, 브램블, 안식처 등 트리 분해 이외의 구조에서도 정의할 수 있습니다.

주어진 그래프 G가 최대 주어진 변수 [4]k를 가지는지 여부를 결정하는 것은 NP-완전이다.그러나 k가 임의의 고정 상수일 경우 트리 폭 k의 그래프를 인식하고 이를 위해 구성된 너비 k 트리 분해를 선형 [3]시간으로 인식할 수 있다.k에 대한 이 알고리즘의 시간 의존성은 k의 지수3 함수입니다.

동적 프로그래밍

1970년대 초에 그래프에 정의된 많은 조합 최적화 문제들은 그래프가 나무 너비와 관련된 변수인 유계 차원을 [5]갖는 한 비직렬 동적 프로그래밍에 의해 효율적으로 해결될 수 있다는 것이 관찰되었다.이후, 1980년대 [6]말, 몇몇 저자들은 임의 그래프에 대해 NP-완전한 많은 알고리즘 문제가 이 그래프의 트리 분해를 사용하여 유계 트리 폭의 그래프에 대한 동적 프로그래밍에 의해 효율적으로 해결될 수 있다고 독립적으로 관찰했다.

예를 들어, 나무 너비 k의 그래프에서 최대 독립 집합을 찾는 문제를 고려하십시오.이 문제를 해결하려면 먼저 트리 분해 노드 중 하나를 임의로 루트로 선택합니다.트리 분해의 노드i X의 경우 X를 X에서i 내림차순 집합j X의 결합으로i 합니다.독립적인 세트 들어 S⊂ X나는,{\displaystyle S\subset X_{나는},}자 A(S,i)를 나타낸 크기로 가장 큰 독립된 부분 집합의 자이가 나는 ∩ X나는 정도 S.{\displaystyle I\cap X_{나는}=S.}이와 마찬가지로,에 대한 인접한 한쌍의 노드 자이와 Xj과 자이 더 멀리에서 뿌리의 나무보다 Xj고, 독립된 세트 S⊂ X i , {\}\capj} B(S,i,j)는 X의 가장 큰 독립 서브셋 I의i 크기를 나는 } S . {\\cap}이다

여기서 A ,)({ A)}의 합계는 노드i X의 자식 위에 있습니다.

각 노드 또는 에지에는 이러한 값을 계산해야 하는 세트 S가 최대k 2개 있습니다. 따라서 k가 상수이면 전체 계산에는 에지 또는 노드당 일정한 시간이 걸립니다.maximum independent set의 크기는 루트 노드에 저장되어 있는 최대값이며, 이 최대값부터 시작하여 저장된 값을 역추적함으로써 (다이나믹 프로그래밍 알고리즘에서 표준과 같이) 최대 독립적 set 자체를 찾을 수 있습니다.따라서, 유계 트리 폭의 그래프에서, 최대 독립 집합 문제는 선형 시간 내에 해결될 수 있다.유사한 알고리즘이 다른 많은 그래프 문제에도 적용됩니다.

이 동적 프로그래밍 접근법은 제한 트리 폭의 그래프에서 믿음 전파를 위한 접합 트리 알고리즘을 통한 기계 학습에 사용된다.그것은 또한 나무 너비를 계산하고 나무 분해를 구성하기 위한 알고리즘에서 중요한 역할을 한다: 일반적으로, 그러한 알고리즘은 나무 너비를 근사하는 첫 번째 단계를 가지고, 이 대략적인 너비로 나무 분해를 구성하며, 그리고 나서 compu에 대한 대략적인 나무 분해를 수행하는 두 번째 단계를 가진다.트리 [3]폭의 정확한 값을 지정합니다.

「 」를 참조해 주세요.

  • 브램블과 안식처– 그래프의 트리폭을 정의할 때 트리 분해의 대안으로 사용할 수 있는2종류의 구조입니다.
  • 분기 분해 – 너비가 일정한 트리 폭 내에 있는 밀접하게 관련된 구조입니다.
  • 분해 방법 – 트리 분해는 제약조건 만족 문제를 해결하기 위해 분해 방법에서 사용한다.

메모들

  1. ^ 디에스텔 (2005) 페이지 354–355
  2. ^ 다이스텔 (2005)섹션 12.3
  3. ^ a b c 보드렌더(1996년).
  4. ^ Arnborg, Corneil & Proskurowski(1987년).
  5. ^ Bertelé & Brioschi(1972년).
  6. ^ Arnborg & Proskurowski(1989년), Bern, Lawler & Wong(1987년), Bodlaender(1988년).

레퍼런스

  • 를 클릭합니다Arnborg, S.; Corneil, D.; Proskurowski, A. (1987), "Complexity of finding embeddings in a k-tree", SIAM Journal on Matrix Analysis and Applications, 8 (2): 277–284, doi:10.1137/0608024.
  • 를 클릭합니다Arnborg, S.; Proskurowski, A. (1989), "Linear time algorithms for NP-hard problems restricted to partial k-trees", Discrete Applied Mathematics, 23 (1): 11–24, doi:10.1016/0166-218X(89)90031-0.
  • 를 클릭합니다Bern, M. W.; Lawler, E. L.; Wong, A. L. (1987), "Linear-time computation of optimal subgraphs of decomposable graphs", Journal of Algorithms, 8 (2): 216–235, doi:10.1016/0196-6774(87)90039-3.
  • 를 클릭합니다Bertelé, Umberto; Brioschi, Francesco (1972), Nonserial Dynamic Programming, Academic Press, ISBN 0-12-093450-7.
  • 를 클릭합니다Bodlaender, Hans L. (1988), "Dynamic programming on graphs with bounded treewidth", Proc. 15th International Colloquium on Automata, Languages and Programming, Lecture Notes in Computer Science, vol. 317, Springer-Verlag, pp. 105–118, doi:10.1007/3-540-19488-6_110.
  • 를 클릭합니다Bodlaender, Hans L. (1996), "A linear time algorithm for finding tree-decompositions of small treewidth", SIAM Journal on Computing, 25 (6): 1305–1317, CiteSeerX 10.1.1.113.4539, doi:10.1137/S0097539793251219.
  • 를 클릭합니다Diestel, Reinhard (2005), Graph Theory (3rd ed.), Springer, ISBN 3-540-26182-6.
  • 를 클릭합니다Halin, Rudolf (1976), "S-functions for graphs", Journal of Geometry, 8: 171–186, doi:10.1007/BF01917434.
  • 를 클릭합니다Robertson, Neil; Seymour, Paul D. (1984), "Graph minors III: Planar tree-width", Journal of Combinatorial Theory, Series B, 36 (1): 49–64, doi:10.1016/0095-8956(84)90013-3.