동적 프로그래밍

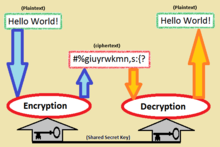
그림 1최적의 하부구조를 사용하여 그래프에서 최단경로를 찾는 것.직선은 단일 에지를 나타내고, 물결선은 연결된 두 정점 사이의 최단경로를 나타냅니다(다른 경로 중 표시되지 않고 동일한 두 정점을 공유함). 굵은 선은 시작부터 목표까지의 전체 최단경로를 나타냅니다.

동적 프로그래밍은 수학적 최적화 방법이자 컴퓨터 프로그래밍 방법입니다.이 방법은 1950년대에 Richard Bellman에 의해 개발되었으며 항공우주공학에서 경제학까지 다양한 분야에서 응용되고 있습니다.

두 가지 상황에서 복잡한 문제를 재귀적인 방식으로 단순한 하위 문제로 분해하여 단순화하는 것을 의미합니다.일부 의사결정 문제는 이러한 방식으로 분리할 수 없지만, 여러 시점에 걸친 결정은 종종 반복적으로 분리됩니다.마찬가지로 컴퓨터 공학에서도 문제를 하위 문제로 나누어 반복적으로 하위 문제에 대한 최적의 해결책을 찾아냄으로써 문제를 최적으로 해결할 수 있다면, 그것은 최적의 하위 구조를 가지고 있다고 할 수 있다.

하위 문제가 더 큰 문제 안에 재귀적으로 중첩되어 동적 프로그래밍 방법을 적용할 수 있는 경우, 더 큰 문제의 값과 하위 문제의 ^[1]값 사이에 관계가 있습니다.최적화 문헌에서는 이 관계를 벨만 방정식이라고 부릅니다.

개요

수학적 최적화

수학적 최적화 측면에서 동적 프로그래밍은 일반적으로 결정을 시간에 따른 일련의 결정 단계로 분해하여 단순화하는 것을 말합니다.이는 y를 1에서 n까지의 시간 i의 시스템 상태를 나타내는 인수로 사용하는 값 함수₁ V, V₂, ..., V의_n 시퀀스를 정의함으로써 이루어집니다.V(y)의 정의는_n 마지막 시간 n의 상태 y에서 얻은 값입니다.이전의 i = n -1, n - 2, ..., 2, 1의 값_i V는 벨만 방정식이라고 불리는 재귀 관계를 사용하여 역방향 작업을 통해 찾을 수 있습니다.i = 2, ..., n에 대해, 임의의 상태 y에서의 V는_i−1, 시각 i - 1에서의 결정에 의한 이득의 단순 함수(통상 합계)와 이 결정이 내려지면 시스템의 새로운 상태에서의 함수_i V를 최대화하여 V로부터 계산한다_i.필요한 상태에 대해 V이 이미 계산되었으므로 위의_i 작업을 수행하면 해당 상태에 대한 V이 생성됩니다_i−1.마지막으로 시스템의 초기 상태에서의 V는 최적₁ 솔루션의 값입니다.의사결정 변수의 최적값은 이미 수행된 계산을 추적하여 하나씩 복구할 수 있습니다.

제어 이론

제어이론에서 일반적인 $\mathbf {u} ^{\ast }$ 는 ${\dot {\mathbf {x} }}(t)=\mathbf {g} \left(\mathbf {x} (t),\mathbf {u} (t),t\right)$ x ${\dot {\mathbf {x} }}(t)=\mathbf {g} \left(\mathbf {x} (t),\mathbf {u} (t),t\right)$ δ ( ${\dot {\mathbf {x} }}(t)=\mathbf {g} \left(\mathbf {x} (t),\mathbf {u} (t),t\right)$ t ) ${\dot {\mathbf {x} }}(t)=\mathbf {g} \left(\mathbf {x} (t),\mathbf {u} (t),t\right)$ ( ${\dot {\mathbf {x} }}(t)=\mathbf {g} \left(\mathbf {x} (t),\mathbf {u} (t),t\right)$ ( ${\dot {\mathbf {x} }}(t)=\mathbf {g} \left(\mathbf {x} (t),\mathbf {u} (t),t\right)$ ) , ${\dot {\mathbf {x} }}(t)=\mathbf {g} \left(\mathbf {x} (t),\mathbf {u} (t),t\right)$ u ( ${\dot {\mathbf {x} }}(t)=\mathbf {g} \left(\mathbf {x} (t),\mathbf {u} (t),t\right)$ ) , ${\dot {\mathbf {x} }}(t)=\mathbf {g} \left(\mathbf {x} (t),\mathbf {u} (t),t\right)$ ) \ $display$ style $\$ $mathbf$ $\mathbf {u} ^{\ast }$ { x } } （ t ${\dot {\mathbf {x} }}(t)=\mathbf {g} \left(\mathbf {x} (t),\mathbf {u} (t),t\right)$ = \ $mathbf {g }$ \ left \ $mathb$ { t $\mathbf {u} ^{\ast }$ } ) ${\dot {\mathbf {x} }}(t)=\mathbf {g} \left(\mathbf {x} (t),\mathbf {u} (t),t\right)$ $、$ ${\dot {\mathbf {x} }}(t)=\mathbf {g} \left(\mathbf {x} (t),\mathbf {u} (t),t\right)$ （ t $）$ 。 $\mathbf {x} ^{\ast }$ 비용 $\mathbf {x} ^{\ast }$ $함수$ 를 최소화하는 연속 시간 $t_{0}\leq t\leq t_{1}$ $t_{0}\leq t\leq t_{1}$ 0 $t_{0}\leq t\leq t_{1}$ t $t_{0}\leq t\leq t_{1}$ { \ $displaystyle$ t $_$ $\mathbf {x} ^{\ast }$ { $0$ $t_{0}\leq t\leq t_{1}$ } \ $\mathbf {x} ^{\ast }$ $leq$ t _ { { $t_{0}\leq t\leq t_{1}$ $}$ } $。$

\displaystyle J=b\left(\mathbf {x}(t_{1}), t_{1}\right)+\int _{t_{1}f\left(\mathbf {x}(t),\mathbf {u}(t,t\right)\mathrm {d} t}

이 문제에 대한 해결책은 $\mathbf {x} ^{\ast }$ 의 제어법칙 또는 $\mathbf {u} ^{\ast }=h(\mathbf {x} (t),t)$ u $\mathbf {u} ^{\ast }=h(\mathbf {x} (t),t)$ $\mathbf {u} ^{\ast }=h(\mathbf {x} (t),t)$ h ( $\mathbf {u} ^{\ast }=h(\mathbf {x} (t),t)$ ( $\mathbf {u} ^{\ast }=h(\mathbf {x} (t),t)$ t ) $\mathbf {u} ^{\ast }=h(\mathbf {x} (t),t)$ , $\mathbf {u} ^{\ast }=h(\mathbf {x} (t),t)$ t ) { $display$ \ $mathbf {$ $u$ } ^ { \ $ast$ $}$ = $h$ ( \ $mathbf$ { $x$ $}$ ( $t$ , $t$ $\mathbf {u} ^{\ast }=h(\mathbf {x} (t),t)$ ) $\mathbf {u} ^{\ast }=h(\mathbf {x} (t),t)$ $}$ h which $\mathbf {x} ^{\ast }$ which a a a a the the the $thestylestylestylestylestylestylestylestylestyle$ j j j j j j j j j j j j j j j j j j j j j j $J^{\ast }$ j j j j j j the j j j j j j j j j j j j j j an an an an an an an an an an an an an an j후자는 동적 프로그래밍의 기본 방정식을 따릅니다.

\displaystyle - J_{t}^{\ast}=\min _{\mathbf {u}\left\{f\left(t),\mathbf {u}(t,t\right)+J_{x}^{\ast {mathsf {T}}\mathbf {g}\left(\mathbf {x}(t),\mathbf {u}(t),t\right\}

해밀턴-야코비-벨만 방정식으로 알려진 편미분 방정식. $J_{x}^{\ast }={\frac {\partial J^{\ast }}{\partial \mathbf {x} }}=\left[{\frac {\partial J^{\ast }}{\partial x_{1}}}~~~~{\frac {\partial J^{\ast }}{\partial x_{2}}}~~~~\dots ~~~~{\frac {\partial J^{\ast }}{\partial x_{n}}}\right]^{\mathsf {T}}$ 서 $J_{x}^{\ast }={\frac {\partial J^{\ast }}{\partial \mathbf {x} }}=\left[{\frac {\partial J^{\ast }}{\partial x_{1}}}~~~~{\frac {\partial J^{\ast }}{\partial x_{2}}}~~~~\dots ~~~~{\frac {\partial J^{\ast }}{\partial x_{n}}}\right]^{\mathsf {T}}$ $J_{x}^{\ast }={\frac {\partial J^{\ast }}{\partial \mathbf {x} }}=\left[{\frac {\partial J^{\ast }}{\partial x_{1}}}~~~~{\frac {\partial J^{\ast }}{\partial x_{2}}}~~~~\dots ~~~~{\frac {\partial J^{\ast }}{\partial x_{n}}}\right]^{\mathsf {T}}$ $J_{x}^{\ast }={\frac {\partial J^{\ast }}{\partial \mathbf {x} }}=\left[{\frac {\partial J^{\ast }}{\partial x_{1}}}~~~~{\frac {\partial J^{\ast }}{\partial x_{2}}}~~~~\dots ~~~~{\frac {\partial J^{\ast }}{\partial x_{n}}}\right]^{\mathsf {T}}$ $=$ J $J_{x}^{\ast }={\frac {\partial J^{\ast }}{\partial \mathbf {x} }}=\left[{\frac {\partial J^{\ast }}{\partial x_{1}}}~~~~{\frac {\partial J^{\ast }}{\partial x_{2}}}~~~~\dots ~~~~{\frac {\partial J^{\ast }}{\partial x_{n}}}\right]^{\mathsf {T}}$ 1 $J_{x}^{\ast }={\frac {\partial J^{\ast }}{\partial \mathbf {x} }}=\left[{\frac {\partial J^{\ast }}{\partial x_{1}}}~~~~{\frac {\partial J^{\ast }}{\partial x_{2}}}~~~~\dots ~~~~{\frac {\partial J^{\ast }}{\partial x_{n}}}\right]^{\mathsf {T}}$ J $J_{x}^{\ast }={\frac {\partial J^{\ast }}{\partial \mathbf {x} }}=\left[{\frac {\partial J^{\ast }}{\partial x_{1}}}~~~~{\frac {\partial J^{\ast }}{\partial x_{2}}}~~~~\dots ~~~~{\frac {\partial J^{\ast }}{\partial x_{n}}}\right]^{\mathsf {T}}$ 1 $J_{x}^{\ast }={\frac {\partial J^{\ast }}{\partial \mathbf {x} }}=\left[{\frac {\partial J^{\ast }}{\partial x_{1}}}~~~~{\frac {\partial J^{\ast }}{\partial x_{2}}}~~~~\dots ~~~~{\frac {\partial J^{\ast }}{\partial x_{n}}}\right]^{\mathsf {T}}$ J $J_{x}^{\ast }={\frac {\partial J^{\ast }}{\partial \mathbf {x} }}=\left[{\frac {\partial J^{\ast }}{\partial x_{1}}}~~~~{\frac {\partial J^{\ast }}{\partial x_{2}}}~~~~\dots ~~~~{\frac {\partial J^{\ast }}{\partial x_{n}}}\right]^{\mathsf {T}}$ partial $J_{x}^{\ast }={\frac {\partial J^{\ast }}{\partial \mathbf {x} }}=\left[{\frac {\partial J^{\ast }}{\partial x_{1}}}~~~~{\frac {\partial J^{\ast }}{\partial x_{2}}}~~~~\dots ~~~~{\frac {\partial J^{\ast }}{\partial x_{n}}}\right]^{\mathsf {T}}$ $J_{x}^{\ast }={\frac {\partial J^{\ast }}{\partial \mathbf {x} }}=\left[{\frac {\partial J^{\ast }}{\partial x_{1}}}~~~~{\frac {\partial J^{\ast }}{\partial x_{2}}}~~~~\dots ~~~~{\frac {\partial J^{\ast }}{\partial x_{n}}}\right]^{\mathsf {T}}$ J partial J $J_{x}^{\ast }={\frac {\partial J^{\ast }}{\partial \mathbf {x} }}=\left[{\frac {\partial J^{\ast }}{\partial x_{1}}}~~~~{\frac {\partial J^{\ast }}{\partial x_{2}}}~~~~\dots ~~~~{\frac {\partial J^{\ast }}{\partial x_{n}}}\right]^{\mathsf {T}}$ x $J_{x}^{\ast }={\frac {\partial J^{\ast }}{\partial \mathbf {x} }}=\left[{\frac {\partial J^{\ast }}{\partial x_{1}}}~~~~{\frac {\partial J^{\ast }}{\partial x_{2}}}~~~~\dots ~~~~{\frac {\partial J^{\ast }}{\partial x_{n}}}\right]^{\mathsf {T}}$ {\ $display style$ J_ ${x$ }^ $frac$ } $rac {\ast }{\frac x_{1}}~~{\frac {\frac x_{2}}~~~~~\frac$ {\frac {\frac $}{\$ frac}{\ $frac$ {\ $ast}}}{\$ frac {\ $f}{\f$ }{\f}}{\ $f$ $J_{t}^{\ast }={\frac {\partial J^{\ast }}{\partial t}}$ 및 $J_{t}^{\ast }={\frac {\partial J^{\ast }}{\partial t}}$ $}{{\f$ }}}}}}{{{\f}}}}}}}}}}}}{~~~~}}}}}}, {\f $J_{x}^{\ast }={\frac {\partial J^{\ast }}{\partial \mathbf {x} }}=\left[{\frac {\partial J^{\ast }}{\partial x_{1}}}~~~~{\frac {\partial J^{\ast }}{\partial x_{2}}}~~~~\dots ~~~~{\frac {\partial J^{\ast }}{\partial x_{n}}}\right]^{\mathsf {T}}$ }, {\f}}}}, {\fright $}$ $\mathbf {u}$ t{\ $displaystyle$ t $t$ $\mathbf {x}$ {\ $displaystyle \mathbf$ { $x$ $\mathbf {x}$ 미지의 $J_{x}^{\ast }$ $J_{x}^{\ast }$ x ${\$ {\ $displaystyle J_{\ast$ }}의 $J_{x}^{\ast }$ { $u}$ 을 $\mathbf {u}$ $($ 를) 계산하여 해밀턴-야코비-벨만 방정식에 대입하여 경계 $J\left(t_{1}\right)=b\left(\mathbf {x} (t_{1}),t_{1}\right)$ J $J\left(t_{1}\right)=b\left(\mathbf {x} (t_{1}),t_{1}\right)$ 로 푼다 $.$ $J\left(t_{1}\right)=b\left(\mathbf {x} (t_{1}),t_{1}\right)$ $J\left(t_{1}\right)=b\left(\mathbf {x} (t_{1}),t_{1}\right)$ 1 $J\left(t_{1}\right)=b\left(\mathbf {x} (t_{1}),t_{1}\right)$ ) , $J\left(t_{1}\right)=b\left(\mathbf {x} (t_{1}),t_{1}\right)$ ) { $style$ J $\left(t_{1}\right)=b\left(\mathbf {x}(t_{1$ }), $t_{1}\$ right $J\left(t_{1}\right)=b\left(\mathbf {x} (t_{1}),t_{1}\right)$ ^[2]실제로, 이것은 정확한 최적화 관계에 대한 이산적인 근사치를 위한 수치 기법을 필요로 한다.

또는 연속 프로세스는 이산 시스템에 의해 근사될 수 있으며, 이는 해밀턴-야코비-벨만 방정식과 유사한 다음과 같은 반복 관계로 이어진다.

J_{k}^{\ast}\left(\mathbf {x}_{n-k}\right)=\min_{\mathbf {u}_{n-k}\left(\mathbf {x}_{n-k},\mathbfu}+오른쪽)J_{k-1}^{\ast}\left({\hat {mathbf {g}}})\left(\mathbf {x} _{n-k},\mathbf {u} _{n-k}\right)\})\right\

k $(\displaystyle$ k $)$ - 동일한 $k$ $n$ 의n(\ $displaystyle$ n $)$ 에서 $n$ f $^{$ { $f$ $}$ ${\hat {\mathbf {g} }}$ g $^$ 은 ${\hat {\mathbf {g} }}$ f $\displaystyle$ f $}$ $\mathbf {g}$ g $(\$ 에 $대한$ 이산 근사치를 나타냅니다.이온 방정식은 벨만 방정식으로 알려져 있으며, 이것은 최적화 ^[3]방정식의 이산 근사치에 대한 정확한 해법으로 풀 수 있다.

경제학의 예: 램지의 최적 절약 문제

경제학에서, 목표는 일반적으로 일부 동적 사회복지 기능을 최대화하는 것이다.램지의 문제에서 이 기능은 소비량과 효용 수준을 연관시킵니다.대략적으로 말하면, 계획자는 동시 소비와 미래 소비 사이의 트레이드오프(생산에서 사용되는 자본 재고에 대한 투자를 통해)에 직면하게 되는데, 이는 시간적 선택으로 알려져 있다.미래 소비는 일정한 $\beta \in (0,1)$ 로 β $\beta \in (0,1)$ β $\beta \in (0,1)$ ( 0 $\beta \in (0,1)$ , $\beta \in (0,1)$ ) $\beta \in (0,1)$ { $displaystyle \beta \in$ ( 0 , $\beta \in (0,1)$ 1 ) $\beta \in (0,1)$ } 。자본의 이행방정식에 대한 이산적 근사치는 다음과 같습니다.

k_{t+1}=hat {g}\left(k_{t},c_{t}\right)=f(k_{t})-c_{t

$c$ 서 c $\displaystyle$ c는 $c$ 소비, $\displaystyle$ k는 $k$ 자본, $\displaystyle$ f는 $f$ 이나다 조건을 충족하는 생산 함수입니다.초기 자본 $k_{0}>0$ $k_{0}>0$ > $k_{0}>0$ { $style$ k _ { $0$ } $>$ 0 이라고 $k_{0}>0$ 가정합니다.

$c$ $c_{t}$ t { $displaystyle$ $c$ $_$ $c_{t}$ { t $c_{t}$ $u(c_{t})=\ln(c_{t})$ } $t$ $u(c_{t})=\ln(c_{t})$ 、소비자가 살아있는 한 소비 $u(c_{t})=\ln(c_{t})$ ( $c$ t ) $= ln$ ( $c$ t $)$ 。소비자는 참을성이 없기 때문에 각 기간마다 $b계수$ 만큼 미래의 효용을 할인한다고 가정합니다. $0<b<1$ 서 0 $0<b<1$ < $0<b<1$ < $0<b<1$ \ $displaystyle$ 0 < $b$ < $1$ . b $0<b<1$ } 。 t 에서는 $k_{t}$ k $k_{t}$ { $displaystyle$ k $_$ { $t$ } 。초기 수도는 주어진 양 k0>0{\displaystyle k_{0}>. 0}일 경우, 이 기간의 자본과 소비 k에게+1)kt A는 긍정적인 편이고 0상수<>를 − c({\displaystyle k_{t+1}=Ak_{t}^{를}-c_{t}},;<1{\displaystyle 0<, a&l을 다음 기간의 자본을 결정한다 가정하다고 가정하자.t;1}. 가정할 수 없어pital은 음수일 수 없습니다.그러면 소비자의 의사결정 문제를 다음과 같이 쓸 수 있습니다.

\max \sum _{t=0}^{T}b^{t}\ln(c_{t})

T}b^{t}\ln(c_{t})

는

\max \sum _{t=0}^{T}b^{t}\ln(c_{t})

모든

t=0,1,2,\ldots ,T

,

t=0,1,2,\ldots ,T

,

T

{\

displaystyle t=0, 2,

…, T {\

dots

k_{t+1}=Ak_{t}^{a}-c_{t}\geq 0

에

k_{t+1}=Ak_{t}^{a}-c_{t}\geq 0

k

k_{t+1}=Ak_{t}^{a}-c_{t}\geq 0

+ 1 =

Ak_{t}^{a}

-

c_{t}

\

geq

0

}

의

k_{t+1}=Ak_{t}^{a}-c_{t}\geq 0

영향을

k_{t+1}=Ak_{t}^{a}-c_{t}\geq 0

.

이렇게 기술하면 이 문제는 복잡해 보입니다.이는 모든 선택 $c_{0},c_{1},c_{2},\ldots ,c_{T}$ c $c_{0},c_{1},c_{2},\ldots ,c_{T}$ $c_{0},c_{1},c_{2},\ldots ,c_{T}$ , $c_{0},c_{1},c_{2},\ldots ,c_{T}$ 2, $c_{0},c_{1},c_{2},\ldots ,c_{T}$ $c_{0},c_{1},c_{2},\ldots ,c_{T}$ $(\$ 에 대한 $k_{0}$ 이 $k_{0}$ 되기 때문입니다( $k_{0}$ k 0 $(\$ displaystyle $k_{0}$ $k_{0})$ 은 선택 변수가 아닙니다.

이 문제를 해결하기 위한 동적 프로그래밍 접근법은 일련의 작은 결정으로 분할하는 것을 포함합니다.이를 위해 t $t=0,1,2,\ldots ,T,T+1$ $t=0,1,2,\ldots ,T,T+1$ , $t=0,1,2,\ldots ,T,T+1$ , $t=0,1,2,\ldots ,T,T+1$ + $t=0,1,2,\ldots ,T,T+1$ (\ $displaystyle$ t $=0,$ 1, $2,\ldots, T, T+1$ )에 $t=0,1,2,\ldots ,T,T+1$ $t=0,1,2,\ldots ,T,T+1$ 값 $V_{t}(k)$ $V_{t}(k)$ t $V_{t}(k)$ ( $V_{t}(k)$ ){ $displaystyle V_{t$ $}($ $k)$ 의 시퀀스를 정의하며, 이는 $t시점$ 의 $임의$ 의 자본금액을 갖는 값을 나타냅니다.사후 자본, $V_{T+1}(k)=0$ + $V_{T+1}(k)=0$ ( $V_{T+1}(k)=0$ ) $=$ {\ $display style V_{T+1$ }(k)=0 $V_{T+1}(k)=0$ 을(를) 보유하는 것은 (추정에 따라) 효용이 없습니다.

이전 자본의 가치는 벨만 방정식을 사용하여 역귀납으로 계산할 수 있습니다.이 문제에서는 각 $t=0,1,2,\ldots ,T$ $t=0,1,2,\ldots ,T$ $t=0,1,2,\ldots ,T$ , $t=0,1,2,\ldots ,T$ , $t=0,1,2,\ldots ,T$ T $(\displaystyle$ t= $0, 1$ , 2, $\ldots, T$ 에 대해 Bellman 방정식은 다음과 같습니다.

V_{t}(k_{t})\,=\,\max \left(\ln(c_{t})+bV_{t+1}(k_{t+1})\right)

( k

V_{t}(k_{t})\,=\,\max \left(\ln(c_{t})+bV_{t+1}(k_{t+1})\right)

)

V_{t}(k_{t})\,=\,\max \left(\ln(c_{t})+bV_{t+1}(k_{t+1})\right)

(

V_{t}(k_{t})\,=\,\max \left(\ln(c_{t})+bV_{t+1}(k_{t+1})\right)

V_{t}(k_{t})\,=\,\max \left(\ln(c_{t})+bV_{t+1}(k_{t+1})\right)

(

V_{t}(k_{t})\,=\,\max \left(\ln(c_{t})+bV_{t+1}(k_{t+1})\right)

t

V_{t}(k_{t})\,=\,\max \left(\ln(c_{t})+bV_{t+1}(k_{t+1})\right)

) +

V_{t}(k_{t})\,=\,\max \left(\ln(c_{t})+bV_{t+1}(k_{t+1})\right)

V

V_{t}(k_{t})\,=\,\max \left(\ln(c_{t})+bV_{t+1}(k_{t+1})\right)

+

V_{t}(k_{t})\,=\,\max \left(\ln(c_{t})+bV_{t+1}(k_{t+1})\right)

(

V_{t}(k_{t})\,=\,\max \left(\ln(c_{t})+bV_{t+1}(k_{t+1})\right)

t +

V_{t}(k_{t})\,=\,\max \left(\ln(c_{t})+bV_{t+1}(k_{t+1})\right)

){

displaystyle V_{t}(k_{t

}),=,\

max \left(\ln(c_{t})+bV_{t+1}(

k_{t+1}=Ak_{t}^{a}-c_{t}\geq 0

{t+1})

의

V_{t}(k_{t})\,=\,\max \left(\ln(c_{t})+bV_{t+1}(k_{t+1})\right)

경우

k - a

k_{t+1}=Ak_{t}^{a}-c_{t}\geq 0

에 따릅니다.

이 문제는 c $\$ 와 $c_{t}$ $k_{t+1}$ t $k_{t+1}$ + $k_{t+1}$ (\ $displaystyle k_{t+1$ 의 2가지 결정 변수만 포함되므로 앞에서 설명한 문제보다 훨씬 단순합니다.직감적으로, 태어날 때 평생의 계획을 선택하는 대신, 소비자는 한 번에 한 단계씩 일을 진행할 수 있습니다. $시간$ t에 현재 $k_{t}$ k $k_{t}$ { $display style$ k _ { $t$ } ,, current $k_{t}$ current current current $c_{t}$ current current current current $c_{t}$ current current current current current current $c_{t}$ c t $c_{t}$ t { $display$ $style$ $c$ _ { $t$ 를 $선택$ 하고 $k_{t+1}$ t + $k_{t+1}$ 을 $k_{t+1}$ 만 하면 됩니다.

실제로 이 문제를 해결하기 위해 우리는 거꾸로 일한다. $V_{T+1}(k)$ 말하면, 현재 자본 수준은 $V_{T+1}(k)$ . $V_{T+1}(k)$ V $V_{T+1}(k)$ + $V_{T+1}(k)$ ( $V_{T+1}(k)$ k $){displaystyle V_{T+1}(k)$ 로 $V_{T+1}(k)$ $표시$ 됩니다.따라서 $V_{T}(k)$ ( k $V_{T}(k)$ )\ $displaystyle V_{T}($ k $V_{T}(k)$ displaystyle V_0 $($ k)\ $style$ V_0(k)\style $(k)$ 에 $V_{0}(k)$ 할 때까지 Bellman 방정식을 사용합니다.평생 동안 문제가 될 수 있습니다.즉, V $V_{T-j+1}(k)$ - $V_{T-j+1}(k)$ j + $V_{T-j+1}(k)$ ( $V_{T-j+1}(k)$ $){$ $displaystyle V_{T-j+1}(k$ $)}{$ $displaystyle V_{T-j}(k$ $\ln(c_{T-j})+bV_{T-j+1}(Ak^{a}-c_{T-j})$ 을 $V_{T-j+1}(k)$ Ln $\ln(c_{T-j})+bV_{T-j+1}(Ak^{a}-c_{T-j})$ T - j) + B $\ln(c_{T-j})+bV_{T-j+1}(Ak^{a}-c_{T-j})$ - 1 $a$ 의 최대값을 $V_{T-j}(k)$ 할 수 있습니다. $aystyle c_{T-j}$ 는 $c_{T-j}$ $Ak^{a}-c_{T-j}\geq 0$ 로 A $Ak^{a}-c_{T-j}\geq 0$ $Ak^{a}-c_{T-j}\geq 0$ - $Ak^{a}-c_{T-j}\geq 0$ T - $Ak^{a}-c_{T-j}\geq 0$ 0 { $display style$ Ak^ { $a$ } - c $_$ { T - $j$ } \ $geq$ 0 $Ak^{a}-c_{T-j}\geq 0$ 。

거꾸로 작업하면 $t=T-j$ t $t=T-j$ T $t=T-j$ - $t=T-j$ \ $displaystyle$ t= $T-j의$ 값 함수는 다음과 같습니다.

V_{T-j}(k),=,a\sum _{i=0}^{j}a^{i}b^{i}\ln k+v_{T-j

$v_{T-j}$ 서 각 $v_{T-j}$ - $v_{T-j}$ (\ $displaystyle v_{T-j})$ 는 $v_{T-j}$ 상수이며 t $t=T-j$ - $t=T-j$ (\ $displaystyle$ t $=T-j)$ $t=T-j$ 에 $t=T-j$ 소비하는 최적의 양은

c_{T-j}(k),=,{\frac {1}{\sum _{i=0}^{j}a^{i}b^{i}}}Ak^{a}

간단히 말하면

{\displaystyle\begin{aligned}c_{T}(k)&{T-1}+a^{T}b^{T}}\end{aligned}}

우리는 나이가 들수록 현재의 부의 더 큰 부분을 소비하고, 마지막으로 삶의 마지막 기간인 T $기간$ 에 남아 있는 모든 부를 소비하는 것이 최적이라는 것을 알 수 있다.

컴퓨터 프로그래밍

동적 프로그래밍을 적용하기 위해서는 최적의 하위 구조와 중복되는 하위 문제라는 두 가지 주요 특성이 있습니다.중복되지 않는 하위 문제에 대한 최적의 솔루션을 결합하여 문제를 해결할 수 있는 경우,^[1] 대신 이 전략을 "분할 후 정복"이라고 합니다.따라서 병합 정렬과 빠른 정렬이 동적 프로그래밍 문제로 분류되지 않습니다.

최적 하부구조란 주어진 최적화 문제에 대한 솔루션을 하위 문제에 대한 최적의 솔루션을 조합하여 얻을 수 있음을 의미합니다.이러한 최적의 하부구조는 보통 재귀에 의해 설명된다.예를 들어 그래프 G=(V,E)가 주어졌을 때, 정점 u에서 정점 v까지의 최단 경로 p는 최적의 서브구조를 나타낸다: 이 최단 경로 p 위의 임의의 중간 정점 w를 취한다.p가 정말로 최단 패스인 경우, p는₁ u에서 w로₂, p는 w에서 v로 분할할 수 있습니다.그러면 대응하는 정점 사이의 최단 패스(알고리즘의 개요에 기재되어 있는 단순한 컷 앤 페이스트 인수에 의해)가 됩니다.따라서 벨만-포드 알고리즘 또는 플로이드-워셜 알고리즘이 하는 것과 같은 최단 경로를 재귀적으로 찾는 솔루션을 쉽게 공식화할 수 있습니다.

하위 문제가 겹친다는 것은 하위 문제의 공간이 작아야 한다는 것을 의미합니다. 즉, 문제를 해결하는 재귀 알고리즘은 동일한 하위 문제를 반복적으로 해결해야 하며, 새로운 하위 문제를 생성하는 것이 아닙니다.예를 들어, Fibonacci 시리즈를 생성하기 위한 재귀적 공식에 대해 생각해 보겠습니다.F_i = F_i−1 + F_i−2(기본 케이스₁ F = F₂ = 1일 경우).그런₄₃ 다음 F = F₄₂ + F₄₁, F₄₂ = F₄₁ + F입니다₄₀.이제₄₁ F는 F와₄₂ F의₄₃ 재귀 하위 트리에서 해결됩니다.하위문제의 총수는 실제로는 적지만(그 중 43개만), 이와 같은 순진한 재귀적 해법을 채택하면 같은 문제를 몇 번이고 풀게 된다.동적 프로그래밍은 이 사실을 고려하여 각 하위 문제를 한 번만 해결합니다.

그림 2피보나치 시퀀스의 하위 문제 그래프.트리가 아니라는 것은 중복되는 하위 문제를 나타냅니다.

이 작업은 다음 두 가지 ^{[citation needed]}방법 중 하나로 수행할 수 있습니다.

톱다운 어프로치:이것은 모든 문제의 재귀적 공식에서 직접 벗어나는 것입니다.하위 문제에 대한 솔루션을 사용하여 문제에 대한 해결책을 반복적으로 작성할 수 있고 하위 문제가 중복될 경우 하위 문제에 대한 해결책을 쉽게 메모하거나 표에 저장할 수 있습니다.새로운 서브 문제를 해결하려고 할 때마다 먼저 표에서 이미 해결되었는지 확인합니다.솔루션이 기록된 경우 직접 사용할 수 있으며, 그렇지 않은 경우 하위 문제를 해결하고 해당 솔루션을 표에 추가합니다.
상향식 어프로치: 서브 문제와 마찬가지로 문제의 해결책을 재귀적으로 작성하면 상향식으로 문제를 재구성할 수 있습니다.하위 문제를 먼저 해결하고 그 솔루션을 사용하여 더 큰 서브 문제에 대한 해결책을 도출할 수 있습니다.이것은 보통 작은 하위 문제에 대한 해결책을 사용하여 크고 큰 하위 문제에 대한 해결책을 반복적으로 생성함으로써 표 형식으로 이루어집니다.예를 들어 F와₄₀ F의 값을₄₁ 이미 알고 있다면 F의 값을₄₂ 직접 계산할 수 있습니다.

일부 프로그래밍 언어에서는 이름별 평가를 고속화하기 위해 함수 호출 결과를 특정 인수 세트로 자동으로 메모할 수 있습니다(이 메커니즘을 필요별 호출이라고 부릅니다).일부 언어(Scheme, Common Lisp, Perl 또는 D 등)는 휴대성을 가능하게 합니다.Tabled Prolog 및 J와 같이 M.^[4] 부사를 사용한 메모 기능을 지원하는 자동 메모 기능이 내장되어 있는 언어도 있습니다.어떤 경우에도 이것은 참조 투과 함수에 대해서만 가능합니다.메모화는 Wolfram Language와 같은 용어 재작성 기반 언어에서 쉽게 접근할 수 있는 설계 패턴으로도 볼 수 있습니다.

생물정보학

동적 프로그래밍은 배열 정렬, 단백질 폴딩, RNA 구조 예측 및 단백질-DNA 결합과 같은 작업을 위해 생물 정보학에서 널리 사용됩니다.단백질-DNA 결합을 위한 최초의 동적 프로그래밍 알고리즘은 1970년대에 미국의^[5] Charles DeLisi와 소련의 ^[6]Georgii Gurskii와 Alexander Zasedatelev에 의해 독립적으로 개발되었다.최근 이러한 알고리즘은 생물정보학 및 계산생물학, 특히 뉴클레오솜 위치결정 및 전사인자 결합 연구에서 매우 인기를 끌고 있다.

예: 컴퓨터 알고리즘

최단 경로 문제에 대한 다이크스트라의 알고리즘

동적 프로그래밍 관점에서, 최단 경로 문제에 대한 Dijkstra의 알고리즘은 도달 방법에 ^[7]^[8]^[9]의한 최단 경로 문제에 대한 동적 프로그래밍 함수 방정식을 푸는 연속 근사 체계입니다.

사실,^[10] Dijkstra의 알고리즘 배후에 있는 논리에 대한 설명, 즉

문제 22개의 $노드$ P $(\displaystyle$ P $)$ 와 $P$ Q $(\displaystyle$ Q $Q$ 사이의 최소 총 길이 경로를 찾습니다.
R $(\displaystyle$ R $)$ 이 $R$ P $(\displaystyle$ P $)$ 에서 $P$ Q $(\displaystyle$ Q $Q$ 로 가는 최소 경로상의 노드인 $경우$ 후자의 지식은 P $(\displaystyle$ P $)$ 에서 $P$ R $(\displaystyle$ R $R$ 로 가는 최소 경로의 지식을 의미합니다.

는 벨만의 유명한 최적성의 원리를 최단 경로 문제의 맥락에서 바꾸어 표현한 것입니다.

피보나치 수열

피보나치 시퀀스의 n번째 멤버 계산에 동적 프로그래밍을 사용하면 성능이 크게 향상됩니다.다음은 수학적 정의에 직접 기반한 순진한 구현입니다.

함수 fib(n): n < 1 리턴 fib(n - 1) + fib(n - 2)

우리가 전화를 걸면,fib(5)여러 번 같은 값으로 함수를 호출하는 콜트리를 만듭니다.

fib(5)
fib(4) + fib(3)
(fib(3) + fib(2)) + (fib(2) + fib(1))
((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
(((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))

특히,fib(2)처음부터 세 번 계산되었습니다.더 큰 예에서는 더 많은 값이fib또는 하위 문제가 다시 계산되어 지수 시간 알고리즘이 발생합니다.

이제 단순한 맵 오브젝트 m이 있다고 가정합니다.m은 각 값을 매핑합니다.fib이미 그 결과에 따라 계산되었으며, 우리는 그것을 사용하기 위해 우리의 기능을 수정하고 그것을 업데이트합니다.결과 함수에는 지수 시간 대신 O(n) 시간만 필요합니다(단, O(n) 공간 필요).

var m : → map(0 → 0, 1 → 1) 키 n이 m[n] 맵에 없는 경우 fib(n) 함수 fib(n):= fib(n - 1) + fib(n - 2)가 m[n]을 반환합니다.

이미 계산된 값을 저장하는 이 기법을 메모화라고 합니다.이것은 우선 문제를 하위 문제로 분류하고 다음으로 값을 계산하여 저장하기 때문에 하향식 접근법입니다.

상향식 접근법에서는 다음과 같은 작은 값을 계산합니다.fib먼저, 그것들로부터 더 큰 가치를 만들어라.이 방법은 또한 n - 1회 반복되는 루프를 포함하므로 O(n) 시간을 사용하지만 맵을 저장하기 위해 O(n) 공간을 필요로 하는 하향식 접근 방식과는 달리 일정(O(1) 공간만 사용합니다.

함수 fib(n) n = 0이면 var previousFib : = 0을 반환하고 그렇지 않으면 currentFib : = 1 var newFib : = previousFib + currentFib : = currentFib currentFib : = newFib returrentFib currentFib : = currentFib ReturrentFib : //ibibibibibibibibibib isibFib loop isibFib loopFib functionFib functionFib

두 가지 예에서 우리는 단지 계산한다.fib(2)한 번, 그리고 두 번 모두 계산하기 위해 사용합니다.fib(4)그리고.fib(3)둘 중 하나가 평가될 때마다 계산하는 것이 아니라

위의 방법에서는 큰n의 경우 실제로는 $\Omega (n^{2})$ $\Omega (n)$ ( $n$ $\Omega (n)$ displaystyle $\Omega (n)$ $\$ Omega $(n^{$ 2})시간이 $\Omega (n^{2})$ 걸립니다.이는 각각 $\Omega (n)$ ( $)\displaystyle$ $\Omega$ ( $n)$ 비트를 $\Omega (n)$ 가진 2개의 정수를 더하면 $\Omega (n)$ (n $)\displaystyle$ \Omega ( $n)$ 비트가 $\Omega (n)$ 필요하기 때문입니다.(n fibonacci 번호에는^th $\Omega (n)$ ( $)\displaystyle \Omega (n)}$ 비트가 $\Omega (n)$ 있습니다).또한 비넷 공식으로 알려진 피보나치 시퀀스의 닫힌 형식이 있으며 $,$ 여기서 $n번째$ $n$ 을 $n$ $O(n(\log n)^{2})$ O $O(n(\log n)^{2})$ $O(n(\log n)^{2})$ $))$ 2 $displaystyle$ O $(n(\log$ n $)^2})$ 시간으로 $O(n(\log n)^{2})$ 계산할 수 있으며, 이는 위의 동적 프로그래밍 기술보다 효율적이다.단, 단순 반복은 빠른 매트릭스 지수에 의해 $O(n\log n)$ O $O(n\log n)$ log $O(n\log n)$ n $)\style$ O $(n\log$ n $)$ 알고리즘으로 $O(n\log n)$ 이어지는 매트릭스 형식을 직접 제공합니다.

균형잡힌 0-1 행렬의 유형

각 행과 각 열에 정확히 $/2개$ 의 0과 $/2개$ 의 1이 포함되도록 짝수 행렬의 위치에 0 또는 1의 값을 할당하는 문제를 고려합니다. $주어진$ n{\ $displaystyle$ n $n$ 에 대해 몇 가지 다른 과제가 있는지 물어봅니다. 예를 들어 = $4$ 인 경우, 5가지 가능한 솔루션은

{\displaystyle{\begin{bmatrix}0&, 1&, 0&, 1\\1&, 0&, 1&, 0\\0&, 1&, 0&, 1\\1&, 0&, 1&, 0\end{bmatrix}}{\text{과}}{\begin{bmatrix}0&, 0&, 1&, 1\\0&, 0&, 1&, 1\\1&, 1&, 0&, 0\\1&, 1&, 0&, 0\end{bmatrix}}{\text{과}}{\begin{bmatrix}1&, 1&, 0&, 0\\0&, 0&, 1&, 1\\1&, 1&, 0&, 0\\0&am.P;0&, 1&, 1\end{bmatrix}}{\text{과}}{\begin{bmatrix}1&, 0&, 0&, 1\\0&, 1&, 1&, 0\\0&, 1&, 1&, 0\\1&, 0&, 0&, 1\end{bmatrix}}{\text{과}}{\begin{bmatrix}1&, 1&, 0&0.\\1&0&0\0&1\0&1\0&1\end{bmatrix}.}

적어도 3가지 접근법이 있습니다.블루트 포스, 백트랙, 다이내믹 프로그래밍입니다.

브루트 포스는 0과 1의 모든 할당을 체크하고 균형 잡힌 행과 열 $(n$ / $2$ 0과 / $2$ 1)을 가진 할당을 카운트하는 것으로 구성됩니다.가능한 할당은 $({$ 2})와 $2^{n^2}$ ${\tbinom {n}{n/2}}^{n}$ ( ${$ 2}} $개({$ $displaystyle$ n $=6$ 가 $2^{n^{2}}$ 때문에 이 전략은 $n=6$ 이지 않습니다.

이 문제의 백트래킹은 매트릭스 요소의 순서를 선택하고 1 또는0을 재귀적으로 배치하는 것으로 구성됩니다.또한 모든 행과 컬럼에서 할당되지 않은 요소의 수와1 또는 0의 수가 $모두$ 2 이상인지 확인합니다.이 접근 방식은 폭력보다 더 정교하지만 모든 솔루션을 한 번 방문하므로 6개 이상의 솔루션에서는 실용적이지 않습니다. = 8의 솔루션 수가 이미 116,963,796,250개이기 때문입니다.

동적 프로그래밍을 통해 모든 솔루션을 방문하지 않고도 솔루션 수를 셀 수 있습니다.첫 번째 행의 역추적 값을 상상해 보십시오. 각 첫 번째 행 값에 대해 얻은 솔루션을 정확하게 계산하려면 나머지 행에 대해 어떤 정보가 필요합니까?× 보드를 고려합니다. $여기$ 서 1 ≤ , $。$ $k$ 행에는 n/ $(\displaystyle$ n/ $2)$ 의 $n/2$ $n/2$ 과 $/$ 2(\ $displaystyle n$ /2 $)$ 의 $n/2$ 0이 $n/2$ 됩니다.메모화가 적용되는 함수 f는 n쌍의 정수 벡터를 허용 보드(솔루션) 수에 매핑한다.각 열에 대해 하나의 쌍이 있으며, 두 개의 구성요소는 각각 0의 수와 해당 열에 아직 배치되지 않은 1의 수를 나타냅니다. $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ ( ( $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ / $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ , n / $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ 2 ) $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ , $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ ( $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ / $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ 2 , $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ / $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ 2 ) $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ , $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ ( $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ / $2$ , n / $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ ) $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ , $displaystyle$ f ( ( $n$ / $2, n$ / $2$ ) , $n$ / 2 ) , \ $ldots ( n$ / $2,$ n / $2$ ) 、、 $f((n/2,n/2),(n/2,n/2),\ldots (n/2,n/2))$ \ $display style$ n $elements$ or vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector vector 。하위 문제 생성 프로세스에서는 보드의 맨 위 행에 대해 가능한 모든 ${\tbinom {n}{n/2}}$ $($ 2)을 반복하고 모든 열을 검토하여 맨 위 할당 여부에 따라 해당 열에 대한 쌍의 적절한 요소에서 하나를 빼야 합니다.행에 해당 위치에 0 또는 1이 포함되어 있습니다.결과 중 하나가 음수인 경우 할당은 무효이며 솔루션 세트에 영향을 주지 않습니다(재귀 중지).그렇지 않으면 × 보드의 맨 위 행에 할당하고 나머지 $k$ (- $1)$ × 보드에 대한 솔루션 수를 재귀적으로 계산하여 맨 위 행의 모든 허용 가능한 할당에 대한 솔루션 수를 더하고 합계를 반환합니다.기본 케이스는 1 × $보드$ 에서 발생하는 사소한 하위 문제입니다.The number of solutions for this board is either zero or one, depending on whether the vector is a permutation of $n / 2$ $(0,1)$ and $n / 2$ $(1,0)$ pairs or not.

예를 들어, 위에 표시된 첫 번째 두 개의 보드에서 벡터의 시퀀스는 다음과 같습니다.

((2, 2)(2, 2)(2, 2)(2, 2)(2, 2)(2, 2)(2, 2) k = 4 0 1 0 0 1 ((1, 2) (2, 1) (1, 2) (2), (2) (1, 2) (2), (2) (2), (2) (2), (2) (2) (2) (1) (1) (2) (1) (2) (2) (2, (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2)) (2)) (2) (2)) (2)) (2)) (2)) (2)) (2) (2)) (2)) (2)) (2)) (2) (2)2 0 1 1 0 ( (0, 1) (0, 0) (0, 0) (0, 0) (0, 1) (0, 1) (1, 0) k = 1 1 0 1 0 (0, 0) (0, 0) (0, 0) (0, 0) (0, 0) (0, 0) (0, 0) (0) (0, 0)

솔루션의 수(OEIS의 시퀀스 A058527)는 다음과 같습니다.

(\displaystyle 1,2,90,297200,4209696250,6736218287430460752,\ldots}

동적 프로그래밍 접근법의 MAPLE 구현에 대한 링크는 외부 링크에서 찾을 수 있습니다.

체커보드

n × n 제곱과 비용 함수를 가진 체커보드를 고려합니다.c(i, j)제곱과 관련된 비용이 반환됩니다.(i,j)(i노를 젓는다는 건j컬럼이 됩니다).예를 들어 (5 × 5 체커보드에서는)

	1	2	3	4	5
5	6	7	4	7	8
4	7	6	1	1	4
3	3	5	7	8	2
2	–	6	7	0	–
1	–	–	5	–	–

따라서c(1, 3) = 5

예를 들어, 첫 번째 순위(즉, 행)의 어느 사각형에서도 시작할 수 있는 체커가 있으며, 마지막 순위에 도달하기 위한 최단 경로(방문한 각 순위에서의 최소 비용의 합계)를 알고 싶다고 합시다.체커가 대각선 왼쪽, 대각선 오른쪽 또는 직진할 수 있다고 가정합니다.즉, 체크인이(1,3)로 이동할 수 있다(2,2),(2,3)또는(2,4).

	2	3	4
5
4
3
2	x	x	x
1		o

이 문제는 최적의 하부 구조를 나타냅니다.즉, 전체 문제에 대한 해결책은 하위 문제에 대한 해결책에 의존합니다.함수를 정의하겠습니다.q(i, j)~하듯이

q(i, j) = 제곱(i, j)에 도달하기 위한 최소 비용.

랭크부터 시작n순위를 매겨야 한다.1각 연속 순위에서 모든 제곱에 대해 이 함수의 값을 계산합니다.각 순위에서 최소값을 유지하는 정사각형을 선택하면 순위 사이의 최단 경로를 얻을 수 있습니다.n랭크1.

함수q(i, j)아래 3개의 정사각형 중 하나에 도달하기 위한 최소 비용과 같습니다(이것들만이 이 정사각형에 도달할 수 있기 때문입니다).+c(i, j). 예:

	2	3	4
5
4		A
3	B	C	D
2
1

q(A)=\min(q(B),q(C),q(D)+c(A),

자, 이제 정의해 봅시다.q(i, j)좀 더 일반적인 용어로:

q(i,j)=syslog{cases}\infty&j>n\c(i,j)&i=1\min(q(i-1,j),q(i-1,j+1)+c(i,j)&{text}j>n\in(xtext}).}}\end {case}

이 방정식의 첫 번째 행은 색인이 찍힌 정사각형으로 모델링된 보드를 다룬다.1최저한으로n가장 높은 곳에서두 번째 줄은 첫 번째 순위에서 발생하는 작업을 나타냅니다. 즉, 기본 사례를 제공합니다.세 번째 줄인 재귀가 중요한 부분입니다.이 값은A,B,C,D를 참조해 주세요.이 정의에서 우리는 다음의 간단한 재귀 코드를 도출할 수 있다.q(i, j)다음 의사 코드에서는n보드의 크기입니다.c(i, j)비용 함수입니다.min()는 최소 개수의 값을 반환합니다.

i = 1이 c(i, j)를 반환하는 경우 j < 1 또는 j > n이 무한대를 반환하는 경우 함수 minCost(i, j)가 반환되는 경우 minCost(i, j), minCost(i-1, j), minCost(i-1, j) + c(i, j)

이 함수는 실제 경로가 아닌 경로 비용만 계산합니다.다음은 실제 경로에 대해 설명합니다.이것은 피보나치 번호의 예와 마찬가지로 중복되는 서브 문제의 속성을 나타내기 때문에 매우 느립니다.즉, 동일한 경로 비용을 반복적으로 계산합니다.그러나 경로 비용을 2차원 어레이에 저장하면 상향식으로 훨씬 빠르게 계산할 수 있습니다.q[i, j]기능을 사용하기보다는요.이것에 의해, 어레이에 필요한 모든 값을 재계산할 필요가 없어집니다.q[i, j]한 번만 미리 계산됩니다.사전 계산된 값(i,j)필요할 때마다 검색만 하면 됩니다.

또한 실제 최단 경로가 무엇인지 알아야 합니다.이를 위해 다른 어레이를 사용합니다.p[i, j]; 이전 어레이.이 배열은 임의의 사각형으로의 경로를 기록합니다.s의 전신s지수에 상대적인 오프셋으로 모델링됩니다.q[i, j]미리 계산된 패스 코스트)의s전체 경로를 재구성하기 위해 이전 경로를 검색했습니다.s그 다음에 그 사각형, 그 사각형, 그 사각형, 그 사각형, 그리고 그 사각형, 그리고 그 사각형, 그리고 그 사각형, 그리고 그 사각형에 도달할 때까지 반복됩니다.다음의 의사 코드에 대해 검토합니다.

함수 computeShortestPathArrays() - 1 ~n q[1, x] : = 1 ~n q [ y , 0 ] : = infinity q [ y , n + 1 ] : = 1 ~n m : = min ( q [ y - 1 , x - 1 , x ) ]p[y, x] : = m = q[y-1, x] p[y, x] : = 0 else p[y, x] : = 1

이제 나머지는 최소값을 찾아 인쇄하는 간단한 문제입니다.

함수 computeShortestPath() computeShortestPathArrays() minIndex : = 1min : = q[n, i]의 경우 2 ~ n <minIndex : = imin : = q[n, i] printPath (n, i)

함수 printPath(y, x) print(x) print(x))<-") y = 2 print(x + p[y, x])이면 printPath(y-1, x + p[y, x])

시퀀스 얼라인먼트

유전학에서 시퀀스 정렬은 동적 프로그래밍이 ^[11]필수적인 중요한 응용 프로그램입니다.일반적으로 이 문제는 요소를 교체, 삽입 또는 삭제하는 편집 작업을 사용하여 시퀀스를 다른 시퀀스로 변환하는 것으로 구성됩니다.각 작업에는 관련 비용이 있으며, 목표는 총 비용이 가장 낮은 편집 순서를 찾는 것입니다.

이 문제는 자연스럽게 재귀라고 할 수 있습니다.시퀀스 A는 다음 중 하나에 의해 시퀀스B로 최적으로 편집됩니다.

B의 첫 번째 문자를 삽입하고 A와 B의 꼬리를 최적으로 정렬하는 것
A의 첫 번째 문자를 삭제하고 A와 B의 꼬리를 최적으로 정렬합니다.
A의 첫 번째 문자를 B의 첫 번째 문자로 대체하고 A와 B의 꼬리를 최적으로 정렬합니다.

부분 정렬은 매트릭스로 표로 작성할 수 있으며, 셀(i,j)에는 A[1..i]와 B[1..j]의 최적 정렬 비용이 포함됩니다.셀 내 비용(i,j)은 인접 셀의 비용에 관련 운영 비용을 더하고 최적 셀을 선택하여 계산할 수 있습니다.

다른 변종이 존재한다. Smith-Waterman 알고리즘과 Needleman-을 참조한다.운쉬 알고리즘

하노이 탑 퍼즐

하노이 타워 모델 세트 (디스크 8장 포함)

T(4,3)를 위한 하노이 타워 퍼즐의 애니메이션 솔루션.

하노이의 탑 또는 하노이의 탑은 수학 게임 또는 퍼즐이다.3개의 로드와 어떤 로드에도 미끄러질 수 있는 다양한 크기의 디스크로 구성됩니다.이 퍼즐은 원반들이 깔끔하게 쌓여 있는 상태에서 시작되며, 가장 작은 막대기 하나에 크기가 오름차순으로 배열되어 원뿔 모양을 형성합니다.

퍼즐의 목적은 다음 규칙에 따라 전체 스택을 다른 막대로 이동하는 것입니다.

한 번에 하나의 디스크만 이동할 수 있습니다.
각 동작은 로드 중 하나에서 상부 디스크를 꺼내 해당 로드 위에 이미 있을 수 있는 다른 디스크 위에 있는 다른 로드 위로 슬라이딩하는 것으로 구성됩니다.
작은 디스크 위에 디스크를 놓을 수 없습니다.

동적 프로그래밍 솔루션은 함수 방정식을 푸는 것으로 구성됩니다.

S(n,h,t) = S(n-1,h, not(h,t)), S(1,h,t), S(n-1,not(h,t),t)

여기서 n은 이동할 디스크의 수를 나타내고, h는 홈 로드를 나타내고, t는 타깃 로드를 나타내고, t는 세 번째 로드(h,t)를 나타내지 않으며, ";"는 연결을 나타낸다.

S(n, h, t) : 로드 h에서 로드 t로 이동하는 n개의 디스크로 구성된 문제에 대한 =해.

n=1의 경우 S(1,h,t) = "로드 h에서 로드 t로 디스크 이동"과 같은 사소한 문제가 발생합니다(디스크가 하나만 남아 있습니다).

이 솔루션에 필요한 이동 횟수는 2ⁿ - 1입니다. 이동 횟수를 최대화하는 것이 목적이라면 동적 프로그래밍 함수 방정식은 약간 복잡하며ⁿ 3 - 1 이동이 필요합니다.^[12]

계란 떨어뜨리기 퍼즐

다음은 N=2개의 달걀과 H=^[13]36층의 건물에 관련된 이 유명한 퍼즐의 예를 설명합니다.

36층 건물의 어떤 층이 계란을 떨어뜨리기에 안전한지, 그리고 어떤 층이 계란을 착륙할 때 깨지는지를 알고 싶다고 가정해 보자.몇 가지 전제가 있습니다.

넘어진 달걀은 다시 사용할 수 있다.
깨진 달걀은 버려야 한다.
추락의 영향은 모든 달걀에서 동일합니다.
계란이 떨어졌을 때 깨지면, 높은 창문에서 떨어지면 깨진다.
만약 계란이 추락에서 살아남는다면, 그것은 더 짧은 추락에서 살아남을 것이다.
1층 창문에서 달걀이 깨지는 현상도 배제할 수 없고 36층 창문에서도 달걀이 살아남을 가능성도 배제할 수 없다.

만약 계란이 1개만 있고 올바른 결과를 얻기를 원한다면, 실험은 한 가지 방법으로만 할 수 있습니다.1층 창문에서 계란을 떨어뜨리고 살아남으면 2층 창문에서 떨어뜨려라.부서질 때까지 위로 계속 가세요.최악의 경우 이 방법에는 36개의 배설물이 필요할 수 있습니다.계란이 두 개 있다고 가정합니다.모든 경우에 효과가 있다고 보장되는 가장 낮은 계란 투하 횟수는 몇 개입니까?

이 퍼즐에 대한 동적 프로그래밍 함수 방정식을 도출하기 위해, 동적 프로그래밍 모델의 상태를 쌍 s = (n,k)라고 하자.

n = 사용 가능한 테스트 달걀 수, n = 0, 1, 2, 3, ..., N - 1.

k = 아직 테스트할 (연속) 층 수, k = 0, 1, 2, ..., H - 1.

예를 들어, s = (2,6)는 두 개의 테스트 달걀이 있고 6개의 (연속) 층이 아직 테스트되지 않았음을 나타냅니다.프로세스의 초기 상태는 s = (N,H)이며, 여기서 N은 실험 시작 시 사용 가능한 테스트 달걀의 수를 나타낸다.이 과정은 검사란이 더 이상 존재하지 않거나(n = 0), 또는 k = 0 중 먼저 발생하는 경우 종료됩니다.상태 s = (0,k) 및 k > 0에서 종료가 발생하면 테스트가 실패한 것입니다.

자, 이제.

W(n,k) = 프로세스가 상태 s = (n,k)인 경우 최악의 경우 임계 바닥의 값을 식별하는 데 필요한 최소 시행 횟수.

그러면^[14] 알 수 있다

W(n,k) = 1 + min{max(W(n - 1, x - 1), W(n,k - x): x = 1, 2, ..., k }

모든 n > 0에 대해 W(n,0) = 0이고 모든 k에 대해 W(1,k) = k인 경우.n과 k의 값을 체계적으로 증가시키면 이 방정식을 반복 풀기 쉽다.

다른 파라미터화를 사용한 고속 DP 솔루션

위의 용액은 DP용액을 사용할 경우 $O(nk^{2})$ O( $O(nk^{2})$ k $)(\displaystyle$ O( $nk^{$ 2})}시간이 $O(nk^{2})$ $O(nk^{2})$ 됩니다.W $W(n-1,x-1)$ ( $W(n-1,x-1)$ - $W(n-1,x-1)$ $W(n,k-x)$ , $W(n-1,x-1)$ - $W(n-1,x-1)$ $){$ $display style$ W ( $n-1$ , x - 1 )}이 $W(n-1,x-1)$ (가 $)$ x {\ $display style$ W ( n-1 , $x-1$ )의 $x$ $x$ 이 증가하고 있기 $W(n-1,x-1)$ 에 위의 반복에서 $x$ 의x { $displaystyle$ x $}$ 를 $x$ 바이너리 검색하면 O $O(nk\log k)$ ( $O(nk\log k)$ log $O(nk\log k)$ k $W(n,k-x)$ $)$ 의 $O(nk\log k)$ 시간으로 향상할 수 $W(n,k-x)$ . $(\displaystyle$ x $x$ 즉 로컬 $\max(W(n-1,x-1),W(n,k-x))$ W $\max(W(n-1,x-1),W(n,k-x))$ ( $\max(W(n-1,x-1),W(n,k-x))$ - $\max(W(n-1,x-1),W(n,k-x))$ , $\max(W(n-1,x-1),W(n,k-x))$ - $\max(W(n-1,x-1),W(n,k-x))$ 1 $\max(W(n-1,x-1),W(n,k-x))$ ), $\max(W(n-1,x-1),W(n,k-x))$ ( $\max(W(n-1,x-1),W(n,k-x))$ , $\max(W(n-1,x-1),W(n,k-x))$ - $){$ $displaystyle \max$ ( $W$ ( n - 1 , x - $1$ ), $W$ ( $n$ , k - x $)}$ 는 $\max(W(n-1,x-1),W(n,k-x))$ 글로벌 최소값입니다.또한 DP 테이블에 각 셀에 대한 $x$ 의x(\ $displaystyle$ x)를 $x$ 저장하고 이전 셀의 값을 참조함으로써 각 셀에 $대한$ 최적의x(\ $displaystyle$ x $)$ 를 $x$ 일정 시간 내에 찾을 수 있으므로 $O(nk)$ ( $)\displaystyle O$ (nk $)$ $O(nk)$ 으로 $O(nk)$ 향상됩니다.단, 문제의 다른 파라미터화가 수반되는 보다 빠른 해결책이 있습니다.

$(\displaystyle$ k $)$ 는 $k$ $k$ k $(\displaystyle$ k $)$ $k$ 에서 떨어졌을 때 달걀이 깨지는 층의 총수입니다(위의 예는 $(\displaystyle$ k $=37)).$

계란을 깨기 위해 떨어뜨려야 하는 최소 바닥이 m $(디스플레이 스타일$ m $)$ 이라고 합니다.

$f(t,n)$ ( $f(t,n)$ t , $f(t,n)$ ) { $displaystyle$ f ( $t$ , $n$ ) the $f(t,n)$ {\ $、$ t { $displaystyle$ t} trys $t$ $및$ n{ \ $displaystyle$ n}개의 $n$ 계란을 $t$ 하여 구별할 수 있는 m{ $displaystyle$ m $}$ 의 $m$ 최대값으로 $f(t,n)$ .

$t,n\geq 0$ 으로 $f(t,0)=f(0,n)=1$ f $t,n\geq 0$ ( $f(t,0)=f(0,n)=1$ , $f(t,0)=f(0,n)=1$ ) $f(t,0)=f(0,n)=1$ ( $f(t,0)=f(0,n)=1$ , $f(t,0)=f(0,n)=1$ ) $f(t,0)=f(0,n)=1$ $f(t,0)=f(0,n)=1$ \ $displaystyle$ f ( $t$ , 0 ) $= f$ ( 0 , n ) $t,n\geq 0$ $f$ ( 0 , n ) 、 1 、 $t,n\geq 0$ $、$ $t,n\geq 0$ \ $displaystyle$ t $, n$ \ $geq$ 0 $t,n\geq 0$ 。

최적의 전략에서첫 번째 달걀을 떨어뜨리는 바닥이 $디스플레이 스타일$ a라고 $a$ $합시다$ .

첫 번째 달걀이 깨진 $m은$ 1 $(디스플레이 스타일$ 1 $)$ 에서 $1$ a $(디스플레이$ $스타일$ )로, $(디스플레이$ 스타일 $t-1)$ $n-1$ 와 $(디스플레이$ 스타일 $n-1)$ 달걀을 $n-1$ 사용하여 구별할 수 있습니다.

첫 번째 달걀이 깨지지 않았다면 $m$ 은 $m$ $a+1$ + $1($ $디스플레이$ 스타일 $a+1$ ) ~ k $(디스플레이 스타일$ k $)$ 이며 $k$ $(디스플레이$ 스타일 $t-1)$ 시도와 $t-1$ $(디스플레이 스타일$ n $)$ 달걀을 $n$ $t-1$ 하여 구분할 수 있습니다.

$f(t,n)=f(t-1,n-1)+f(t-1,n)$ f $f(t,n)=f(t-1,n-1)+f(t-1,n)$ ( $f(t,n)=f(t-1,n-1)+f(t-1,n)$ , $f(t,n)=f(t-1,n-1)+f(t-1,n)$ ) $f(t,n)=f(t-1,n-1)+f(t-1,n)$ ( $f(t,n)=f(t-1,n-1)+f(t-1,n)$ - $f(t,n)=f(t-1,n-1)+f(t-1,n)$ , $f(t,n)=f(t-1,n-1)+f(t-1,n)$ - $f(t,n)=f(t-1,n-1)+f(t-1,n)$ ) + $f(t,n)=f(t-1,n-1)+f(t-1,n)$ ( $f(t,n)=f(t-1,n-1)+f(t-1,n)$ - $f(t,n)=f(t-1,n-1)+f(t-1,n)$ , $f(t,n)=f(t-1,n-1)+f(t-1,n)$ ) $= f$ ( $t-1$ , $n-1$ ) + f ( $t-1$ , $n$ ) $f(t,n)=f(t-1,n-1)+f(t-1,n)$ } 입니다 $.$

이 문제는 f $f(x,n)\geq k$ ( $f(x,n)\geq k$ , $f(x,n)\geq k$ $f(x,n)\geq k$ \ $display style$ f ( $x$ , $n$ )\ $geq$ k $f(x,n)\geq k$ }의 $최소$ x { $displaystyle$ x $}$ 를 $x$ 찾는 것과 같습니다.

이를 위해{ $\{f(t,i):0\leq i\leq n\}$ ( $\{f(t,i):0\leq i\leq n\}$ , $\{f(t,i):0\leq i\leq n\}$ ) : $\{f(t,i):0\leq i\leq n\}$ i $\{f(t,i):0\leq i\leq n\}$ n $}$ { $displaystyle$ \ { $f$ ( $t$ , $i$ ) : $0$ \ $leq$ i \ $leq$ n $\{f(t,i):0\leq i\leq n\}$ \ } { $displaystyle$ t $t$ }의 $\{f(t,i):0\leq i\leq n\}$ $t$ 로 계산할 $\{f(t,i):0\leq i\leq n\}$ 수 있습니다.이 경우 $O(nx)$ ( $O(nx)$ x $O(nx)$ ) \ $displaystyle$ O ( $nx$ ) 시간이 걸립니다 $O(nx)$ .

따라서 n $n=1$ $(\displaystyle$ n=1 $n=1$ 의 $경우$ 를 별도로 취급할 경우 알고리즘은 O $O(n{\sqrt {k}})$ k $)(\displaystyle$ O $(n{\sqrt {k}))$ 시간이 $O(n{\sqrt {k}})$ $O(n{\sqrt {k}})$ .

그러나 반복 관계는 실제로는 $f(t,n)=\sum _{i=0}^{n}{\binom {t}{i}}$ f $f(t,n)=\sum _{i=0}^{n}{\binom {t}{i}}$ ( $f(t,n)=\sum _{i=0}^{n}{\binom {t}{i}}$ , n ) $f(t,n)=\sum _{i=0}^{n}{\binom {t}{i}}$ $f(t,n)=\sum _{i=0}^{n}{\binom {t}{i}}$ $f(t,n)=\sum _{i=0}^{n}{\binom {t}{i}}$ $f(t,n)=\sum _{i=0}^{n}{\binom {t}{i}}$ $f(t,n)=\sum _{i=0}^{n}{\binom {t}{i}}$ ( $f(t,n)=\sum _{i=0}^{n}{\binom {t}{i}}$ i $f(t,n)=\sum _{i=0}^{n}{\binom {t}{i}}$ ) { $displaystyle$ $f(t,n)=\sum _{i=0}^{n}{\binom {t}{i}}$ f ( $t$ , $n$ $O(n)$ ) $O(n)$ $=$ \ $sum$ _ { $i$ ${\binom {t}{i+1}}={\binom {t}{i}}{\frac {t-i}{i+1}}$ $= 0$ }^{ $n$ $}{\$ $binom$ ${t$ $}{i}}}$ , f $O(n)$ $f$ f f f f f f f f f $O(n)$ 、 ${\binom {t}{i+1}}={\binom {t}{i}}{\frac {t-i}{i+1}}$ ${\binom {t}{i+1}}={\binom {t}{i}}{\frac {t-i}{i+1}}$ ( ${\binom {t}{i+1}}={\binom {t}{i}}{\frac {t-i}{i+1}}$ ( ${\binom {t}{i+1}}={\binom {t}{i}}{\frac {t-i}{i+1}}$ ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ${\binom {t}{i+1}}={\binom {t}{i}}{\frac {t-i}{i+1}}$ ${\binom {t}{i+1}}={\binom {t}{i}}{\frac {t-i}{i+1}}$ but but but but but $} {$ i+1} = $모든$ i $i\geq 0$ ≥ 0 {\ $displaystyle i\geq$ 0}에 $i\geq 0$ ${\frac {t-i} {i+$ 1 ${\binom {t}{i+1}}={\binom {t}{i}}{\frac {t-i}{i+1}}$ } {\ $frac$ { displaystyle i\geq 0 $i\geq 0$ }

f $f(t,n)\leq f(t+1,n)$ ( $f(t,n)\leq f(t+1,n)$ , $f(t,n)\leq f(t+1,n)$ $f(t,n)\leq f(t+1,n)$ $f(t,n)\leq f(t+1,n)$ ( $f(t,n)\leq f(t+1,n)$ + $f(t,n)\leq f(t+1,n)$ , $f(t,n)\leq f(t+1,n)$ $){$ $displaystyle$ $f(t,n)\leq f(t+1,n)$ f ( $t$ , $n$ )\ $leq$ $f(t,n)\leq f(t+1,n)$ $f$ ( $t$ + $1$ , n $O(n\log k)$ ) $t\geq 0$ } $t\geq 0$ 0 $t\geq 0$ 0 0 $0$ $O(n\log k)$ t \ $displaystyle$ t $x$ ( $t$ $+$ 1, n ) $search$ $t$ t t t t $O(n\log k)$ t $O(n\log k)$ search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search search 、 2진검색을 바이너리 검색하여 $O(n\log k)$ O ^[15]( $O(n\log k)$

행렬 연쇄 곱셈

행렬 연쇄 곱셈은 동적 프로그래밍의 효용을 보여주는 잘 알려진 예입니다.예를 들어, 엔지니어링 애플리케이션은 종종 행렬의 체인을 곱해야 합니다.예를 들어 100×100과 같은 큰 차원의 행렬을 찾는 것은 놀라운 일이 아닙니다.따라서 우리의 작업은 $A_{1},A_{2},....A_{n}$ $A_{1},A_{2},....A_{n}$ , $A_{1},A_{2},....A_{n}$ , $A_{1},A_{2},....A_{n}$ 를 곱하는 것이다. $A_{n$ 행렬 곱셈은 가환성이 아니라 연관성이 있습니다.한 번에 곱할 수 있는 행렬은 2개뿐입니다.이 행렬의 사슬을 여러 가지 방법으로 곱할 수 있습니다. 예를 들어 다음과 같습니다.

(A 1 \times A 2) \times A 3) \times ... A n .

A 1 \times((A 2 \timesA 3)\times...)\timesA n)

(A 1 \times A 2) \times (A 3 \times ...) A n)

기타 등등.이 행렬의 사슬을 곱하는 방법은 여러 가지가 있다.이 두 행렬은 모두 동일한 최종 결과를 생성하지만 특정 행렬을 곱하는 데 어느 정도 시간이 걸립니다.행렬 A의 차원이 m×n이고 행렬 B의 차원이 n×q인 경우 행렬 C=A×B는 차원이 m×q이고 m*n*q 스칼라 곱셈이 필요합니다(그림의 목적으로 단순 행렬 곱셈 알고리즘을 사용).

예를 들어 행렬 A, B, C를 곱해 봅시다.이들의 치수는 각각 m×n, n×p, p×s라고 가정하자.매트릭스 A×B×C의 크기는 m×s이며 아래 두 가지 방법으로 계산할 수 있습니다.

Ax(B×C) 이 행렬 곱셈 순서는 nps + mns 스칼라 곱셈이 필요합니다.
(A×B)×C 이 행렬 곱셈 순서는 mnp + mps 스칼라 계산이 필요합니다.

m = 10, n = 100, p = 10 및 s = 1000이라고 가정합니다.따라서 체인을 곱하는 첫 번째 방법에는 1,000,000 + 1,000,000 계산이 필요합니다.두 번째 방법에서는 10,000+100,000의 계산만 필요합니다.물론 두 번째 방법이 더 빠릅니다. 괄호 배열로 행렬을 곱해야 합니다.

따라서 괄호 순서가 중요하며, 최적의 괄호 순서를 찾는 것이 과제입니다.

이 시점에서 우리는 여러 가지 선택지가 있는데, 그 중 하나는 문제를 중복되는 문제로 분할하고 괄호의 최적의 배치를 계산하는 동적 프로그래밍 알고리즘을 설계하는 것입니다.동적 프로그래밍 솔루션은 다음과 같습니다.

행렬 i에서 행렬 j로 행렬의 사슬을 곱하는 데 필요한 최소 스칼라 곱셈 수를 m[i,j]라고 하자. (즉_i, A × ......)× A_j, 즉 i<=j.i <= k < j>가 되도록 일부 행렬 k에서 체인을 분할하고 어떤 조합이 최소 m[i,j]을 생성하는지 알아보려고 한다.

공식은 다음과 같습니다.

i = j, m[i,j] = i < j, m[i,j] = min (m[i,k]+ $p_{i-1}*p_{k}*p_{j}$ [k+1,j] +  $p_{i-1}*p_{k}*p_{j}$ i -  $p_{i-1}*p_{k}*p_{j}$   $p_{i-1}*p_{k}*p_{j}$   $p_{i-1}*p_{k}*p_{j}$   $p_{i-1}*p_{k}*p_{j}$  p $p_{i-1}*p_{k}*p_{j}$  \  $display$  style  $p_{i-1}*p_{k$

여기서 k의 범위는 i ~j - 1입니다

$p_{i-1}$ i - $({$ 은 $p_{i-1}$ 행렬 i의 행 치수입니다.
$p_{k}$ k $(\$ 는 $p_{k}$ 행렬 k의 열 치수입니다.
$p_{j}$ j { $displaystyle p_{j}}$ 는 $p_{j}$ 행렬 j의 열 치수입니다.

이 공식은 다음과 같이 코드화할 수 있습니다. 여기서 입력 파라미터 "chain"은 행렬의 체인입니다. $A_{1},A_{2},...A_{n}$ , $A_{1},A_{2},...A_{n}$ 1, $A_{1},A_{2},...A_{n}$ 2, $A_{1},A_{2},...A_{n}$ $A_{1},A_{2},...A_{n}$ { $1}, A_{2},$ ..., n $(\$ 1}, A_{2}, ...). $A_{n$

함수 OptimalMatrixChainParenthesis(chain) n = i = 1, n m[i,i] = 0 // len = 2, i = 1, n - len + 1 j = i + len - 1 m[i,j] = infinity에 대해 하나의 행렬을 곱하는 데 계산이 필요하지 않으므로 첫 번째 k를 업데이트한다.i, k] + m[k+1, j] +  $p_{i-1}*p_{k}*p_{j}$ - 1 $p_{i-1}*p_{k}*p_{j}$  p  $p_{i-1}*p_{k}*p_{j}$   $p_{i-1}*p_{k}*p_{j}$   $p_{i-1}*p_{k}*p_{j}$  j $p_{i-1}*p_{k}*p_{j}$ {  $displaystyle p_{i-1}*p_{$ k $p_{i-1}*p_{k}*p_{j}$  $}$  /q <m[i, j] // 괄호의 새로운 순서가 m[i, j] = q 업데이트 s[i, j] // k = 를 기록하기 위해 //

지금까지 행렬 i에서 행렬 j로 체인을 곱하는 계산의 최소 수인 모든 $가능$ 한 $m [i$ , j $]$ 에 대한 값을 계산하고 대응하는 "분할점" $s [i,$ $j]$ 를 기록했습니다.예를 들어 $체인 1$ A $\timesA 23 \timesA 4$ ×A를 곱하면 m $[1,$ $3$ ]= $100$ , $s [1,$ 3]= $2$ 로 $판명$ 되면 행렬 1~3에 대한 괄호의 최적 배치는 ( $(A_{1}\times A_{2})\times A_{3}$ × $(A_{1}\times A_{2})\times A_{3}$ $(A_{1}\times A_{2})\times A_{3}$ $($ A_2 $})$ 이다 $(A_{1}\times A_{2})\times A_{3}$

이 알고리즘은 i와 j의 가능한 모든 값에 대한 엔트리를 갖는 "테이블" m[, ] 및 s[, ]를 생성합니다.전체 체인에 대한 최종 해는 m[1, n]이며, s[1, n]에서 상응하는 분할을 합니다.해결책을 푸는 것은 위에서 시작하여 기본 사례(즉, 단일 행렬의 곱셈)에 도달할 때까지 반복됩니다.

따라서 다음 단계는 체인을 실제로 분할하는 것입니다. 즉, 괄호를 (최적적으로) 소속된 위치에 배치하는 것입니다.이 목적을 위해 다음 알고리즘을 사용할 수 있습니다.

Print Optimal Parenthesis (s, i, j) i = j 인쇄 "A"i else print("Print Optimal Parenthesis (s, i, s[i, j] + 1, j) 인쇄 " " " " 인쇄

물론 이 알고리즘은 실제 곱셈에는 유용하지 않습니다.이 알고리즘은 결과가 어떻게 보이는지 보기 위한 편리한 방법입니다.

적절한 분할을 사용하여 행렬을 실제로 곱하려면 다음 알고리즘이 필요합니다.

   기능. 매트릭스 체인 멀티플라이(쇠사슬 부터 1 로. n)       // 최종 매트릭스(예: A1×A2×...)를 반환합니다.×안       Optimal Matrix Chain Parenthesis(쇠사슬 부터 1 로. n)   // 이렇게 하면 s[ . ] 및 m[ . ] "syslog"가 생성됩니다.       Optimal Matrix 곱셈(s, 쇠사슬 부터 1 로. n)  // 실제 곱셈     기능. Optimal Matrix 곱셈(s, i, j)   // 최적의 방법으로 행렬 체인을 Ai에서 Aj로 곱한 결과를 반환합니다.       한다면 i < > j          // 체인을 계속 분할하고 왼쪽과 오른쪽의 행렬을 곱합니다.          왼쪽 = Optimal Matrix 곱셈(s, i, s[i, j])          오른쪽 = Optimal Matrix 곱셈(s, s[i, j] + 1, j)          돌아가다 매트릭스 멀티플라이(왼쪽, 오른쪽)        또 다른 한다면 i = j          돌아가다 아이   // 위치 i의 매트릭스       또 다른           인쇄물 "오류, i <= j는 보류해야 합니다."      기능. 매트릭스 멀티플라이(A, B)    // 두 행렬을 곱하는 함수       한다면 열(A) = 행(B)           위해서 i = 1, 행(A)             위해서 j = 1, 열(B)                C[i, j] = 0                위해서 k = 1, 열(A)                    C[i, j] = C[i, j] + A[i, k]*B[k, j]                 돌아가다 C        또 다른            인쇄물 "오류, 호환되지 않는 차원"

역사

동적 프로그래밍이라는 용어는 1940년대 리처드 벨먼이 최적의 결정을 차례차례 찾아야 하는 문제를 해결하는 과정을 설명하기 위해 처음 사용되었습니다.1953년까지, 그는 특히 더 큰 의사결정 안에 작은 의사결정 ^[16]문제를 내포하는 것을 언급하면서 이것을 현대적인 의미로 개선했고, 그 후 이 분야는 IEEE에 의해 시스템 분석 및 엔지니어링 주제로 인정받았다.벨만의 기여는 벨만 방정식의 이름으로 기억되는데, 벨만은 최적화 문제를 재귀 형식으로 재작성하는 동적 프로그래밍의 중심 결과입니다.

Bellman은 자서전인 Eye of the Hurricane에서 다이내믹 프로그래밍이라는 용어의 이면에 있는 이유를 설명합니다. 자서전:

나는 1950년의 가을 분기를 랜드에서 보냈다.나의 첫 번째 과제는 다단계 의사결정 과정의 이름을 찾는 것이었다.흥미로운 질문은 "다이나믹 프로그래밍이라는 이름은 어디서 유래한 것인가?"입니다.1950년대는 수학 연구에 좋은 시절이 아니었다.워싱턴에 윌슨이라는 아주 흥미로운 신사가 있었습니다.그는 국방부 장관이었고, 사실 그는 "연구"라는 단어에 대한 병적인 두려움과 증오를 가지고 있었다.저는 이 용어를 가볍게 사용하는 것이 아니라 정확하게 사용하고 있습니다.얼굴이 빨개지고 사람들이 그 앞에서 연구라는 용어를 사용하면 폭력적으로 변합니다.그가 수학이라는 용어에 대해 어떻게 느꼈을지 짐작할 수 있을 것이다.RAND Corporation은 공군에 고용되었고, 공군은 기본적으로 Wilson을 상사로 임명했다.그래서 저는 랜드사에서 수학을 하고 있다는 사실로부터 윌슨과 공군을 보호하기 위해 뭔가 해야겠다고 생각했습니다.어떤 제목, 어떤 이름, 내가 선택할 수 있을까?애초에 저는 계획, 의사결정, 사고에 관심이 있었습니다.하지만 계획은 여러 가지 이유로 좋지 않은 단어입니다.그래서 저는 "프로그래밍"이라는 단어를 사용하기로 했습니다.저는 이것이 역동적이고 다단계이며 시간에 따라 달라지는 것이라는 생각을 전달하고 싶었습니다.일석이조라고 생각했어요.완전히 정확한 의미를 가진 단어를 들어봅시다. 즉, 고전적인 물리적 의미에서 역동적인 단어입니다.형용사로서도 매우 흥미로운 성질을 가지고 있습니다.그것은 dynamic이라는 단어를 경멸적인 의미로 사용하는 것은 불가능하다는 것입니다.경멸적인 의미를 부여할 수 있는 조합을 생각해 보세요.그것은 불가능해요.그래서 나는 다이내믹 프로그래밍이 좋은 이름이라고 생각했다.그것은 국회의원조차 반대할 수 없는 것이었다.그래서 나는 그것을 활동용 우산으로 사용했다.
--

다이나믹이라는 단어는 벨먼이 문제의 시간 변동적인 측면을 포착하기 위해 선택한 것이며,^[11] 그 이유는 그것이 인상적으로 들렸기 때문입니다.프로그래밍이라는 단어는 훈련이나 병참을 위한 군사 일정이라는 의미에서 최적의 프로그램을 찾기 위한 방법을 사용하는 것을 의미했다.이 용도는 선형 프로그래밍 및 수학적 프로그래밍의 구문과 동일하며 수학적 ^[17]최적화의 동의어입니다.

그 용어의 유래에 대한 위의 설명은 부족하다.러셀과 노비그가 그들의 책에서 쓴 것처럼, 위의 이야기를 언급하며: "이것은 엄밀하게 사실일 수 없다. 왜냐하면 윌슨 전 대통령이 ^[18]1953년에 국방장관이 되기 전에 (벨먼, 1952년)이라는 용어를 사용한 그의 첫 번째 논문이 나왔기 때문이다."또한, 벨먼을 기억하는 해롤드 쿠슈너의 연설에는 다음과 같은 언급이 있다.쿠슈너가 Bellman에 대해 말한 것을 인용하면 다음과 같습니다.반면, 같은 질문을 했을 때, 그는 Dantzig의 선형 프로그래밍을 다이내믹을 추가함으로써 강화하려고 한다고 대답했습니다.아마도 두 가지 동기가 모두 사실이었을 것이다.