최대 하위 어레이 문제

검체의 시작 위치와 끝 위치를 기준으로 하위 아레이가 어떻게 변화하는지 시각화.각각의 연속적인 하위 배열은 색상의 선에 있는 점으로 표현된다.그 점의 y 좌표는 표본의 합을 나타낸다.그것의 x 좌표는 표본의 끝을 나타내며, 그 색 선에서 가장 왼쪽 점은 표본의 시작을 나타낸다.이 경우 표본을 채취하는 배열이 [2, 3, -1, -20, 5, 10]이다.

컴퓨터 과학에서 최대 합계 하위 배열 문제는 주어진 1차원 배열 A[1...n] 내에서 가장 큰 합을 가진 연속 하위 배열을 찾는 일이다.공식적으로는 $1\leq i\leq j\leq n$ 1 $1\leq i\leq j\leq n$ $1\leq i\leq j\leq n$ $1\leq i\leq j\leq n$ $1\leq i\leq j\leq n$ $1\leq i\leq j\leq n$ n ${\displaystyle$ $i}$ 및 $j$ $j$ 이 $j$ (가) 있는 지수 $i$ ${\displaystyle$ n ${\leq$ i\ $leq$ j\leq j $\leq n$ 을(를) 찾는 작업이 수행된다.

\sum _{x=i}^{j}A[x]

가능한 한 크다. (문제의 일부 공식은 빈 하위 배열도 고려할 수 있다. 관례상 빈 하위 배열의 모든 값의 합은 0이다.)입력 배열 A의 각 숫자는 양수, 음수 또는 0일 수 있다.^[1]

예를 들어, 값 배열 [-2, 1, -3, 4, -1, 2, 1, -5, 4]의 경우, 합계가 가장 큰 연속 하위 배열은 [4, -1, 2, 1]이고 합계는 6이다.

이 문제의 몇 가지 특성은 다음과 같다.

배열에 음수가 아닌 숫자가 모두 포함되어 있으면 문제는 사소한 것이며, 최대 하위 배열이 전체 배열이다.
배열에 모든 양의 숫자가 포함되지 않은 경우, 해결책은 배열의 최대값을 포함하는 크기 1의 하위 배열(또는 허용되는 경우 비어 있는 하위 배열)이다.
여러 개의 서로 다른 하위 Array의 최대 합계가 동일할 수 있다.

이 문제는 짐승의 힘,^[2] 분열과 정복,^[3] 동적 프로그래밍,^[4] 그리고 최단 경로로의 축소를 포함한 몇 가지 다른 알고리즘 기법을 사용하여 해결할 수 있다.^{[citation needed]}

역사

최대 하위 배열 문제는 디지털화된 영상에서 패턴의 최대우도 추정을 위한 단순화된 모델로서 1977년 Ulf Grenander에 의해 제안되었다.^[5]

그르난데르는 실수의 2차원 배열에서 최대 합을 가진 직사각형 서브 어레이를 찾고 있었다.2차원 문제에 대한 짐승-강력 알고리즘은 O(n⁶) 시간에 실행되는데, 이것이 엄청나게 느렸기 때문에, 그레난더는 그것의 구조에 대한 통찰력을 얻기 위해 1차원 문제를 제안했다.그레난더는 O(n²) 시간에 1차원 문제를 해결하는 알고리즘을 도출해 O(n³)의 짐승 같은 힘 작동 시간을 개선했다.^{[note 1]}마이클 샤모스가 그 문제에 대해 들었을 때, 그는 하룻밤 사이에 그것을 위한 O(n log n) 분할-금융 알고리즘을 고안했다.곧이어 샤모스는 제이 카데인이 참석한 카네기 멜론 대학 세미나에서 가능한 한 빠른 ^[5]^[6]^[7]O(n) 시간 알고리즘을 1분 안에 설계한 1차원 문제와 그 역사를 설명했다.^{[note 2]}1982년 데이비드 그리스는 디즈크스트라의 "표준 전략"을 적용하여 동일한 O(n)시간 알고리즘을 얻었고,^[8] 1989년 리처드 버드는 버드-메르텐스 형식주의를 이용하여 순수하게 브루트포스 알고리즘을 대수적으로 조작하여 이를 도출했다.^[9]

그레난더의 2차원 일반화는 카다네의 알고리즘을 서브루틴으로 사용하거나, 분할과 커커 접근법을 통해 O(n³)시간에 해결할 수 있다.거리 매트릭스 곱셈에 기반한 약간 빠른 알고리즘은 타마키&도쿠야마(1998년)와 타카오카(2002년)가 제안했다.훨씬 더 빠른 알고리즘이 존재하지 않는다는 증거가 있다; 어떤 >>0에 대해서도 O(n^3−ε) 시간의 2차원 최대 서브 어레이 문제를 해결하는 알고리즘은 모든 포인터의 최단 경로 문제에 대해 유사하게 빠른 알고리즘을 암시할 것이다.^[10]

적용들

유전적 시퀀스 분석과 컴퓨터 비전 등 여러 분야에서 최대 서브 어레이 문제가 발생한다.

유전체 시퀀스 분석은 단백질 시퀀스의 중요한 생물학적 세그먼트를 식별하기 위해 최대 하위 어레이 알고리즘을 사용한다.^{[citation needed]}이러한 문제에는 보존된 세그먼트, GC가 풍부한 지역, 탠덤 반복, 저복잡성 필터, DNA 결합 도메인, 충전량이 높은 지역 등이 포함된다.^{[citation needed]}

컴퓨터 비전에서는 이미지에서 가장 밝은 영역을 감지하기 위해 비트맵 이미지에 최대 하위 어레이 알고리즘을 사용한다.

카다네의 알고리즘

비어 있는 하위 검사 승인

실행 예
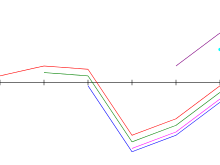
위의 예제에서 카다네의 알고리즘 실행.파란색: i로 끝나는 가장 큰 합이 있는 하위 배열, 녹색: 지금까지 발견된 가장 큰 합이 있는 하위 배열, 소문자는 빈 배열을 나타내며 변수 i는 Python 코드에 암묵적으로 남아 있다.

카다네의 원래 알고리즘은 빈 하위선이 인정될 때 문제 버전을 해결한다.지정된 어레이 $A[1\ldots n]$ [ $A[1\ldots n]$ … $A[1\ldots n]$ $A[1\ldots n]$ $A[1\ldots n]$ 을(를) 왼쪽에서 $A[1\ldots n]$ 오른쪽으로 스캔한다. $j$ $j$ 단계에서 $j$ $j$ ${\displaystyle$ j $}$ 에서 끝나는 $가장$ 큰 합을 사용하여 하위 어레이를 계산하며 $j$ 이 합은 변수로 유지된다.current_sum.^{[note 3]}게다가 변수에서 유지되는 $A[1\ldots j]$ [ $A[1\ldots j]$ … $A[1\ldots j]$ $A[1\ldots j]$ $A[1\ldots j]$ 의 어느 곳에서도 가장 큰 합으로 하위 어레이를 계산한다.best_sum,^{[note 4]} 그리고 모든 값의 최대값으로 쉽게 얻을 수 있다.current_sum지금까지 본 알고리즘의 cf. line 7.

루프 불변성으로, $j$ $j$ th 단계에서 $j$ , 의 이전 값current_sum $A[i]+\cdots +A[j-1]$ $i\in \{1,\ldots ,j\}$ $A[i]+\cdots +A[j-1]$ $i\in \{1,\ldots ,j\}$ , … , $A[i]+\cdots +A[j-1]$ ${\displaystyle$ i $\in \{1,\ldots,j\}$ 합계의 A[ $A[i]+\cdots +A[j-1]$ + $A[i]+\cdots +A[j-1]$ + + A [ 1 $A[i]+\cdots +A[j-1]$ ${\displaystyle A[i]+\cdots$ + $A[j-1]}$ 에 대해 최대값을 유지한다 $A[i]+\cdots +A[j-1]$ ^{[note 5]}그러므로current_sum+A[j]{\displaystyle +A[j]}[노트 6]이 최대에 걸쳐 나는 합의[나는]{1,…, j}{\displaystyle i\in){1,\ldots ,j\}}∈+⋯+A[j]{\displaystyle A[나는]+\cdots +A[j]}. 나는 정도도 경우에 적용되 j+1{\displaystyle i=j+1}, 그것은 또한 빈 subarr을 고려할 충분한 후자 최대 확대하기 위해.아아! $A[j+1\;\ldots \;j]$ [ $A[j+1\;\ldots \;j]$ + $A[j+1\;\ldots \;j]$ … $A[j+1\;\ldots \;j]$ $A[j+1\;\ldots \;j]$ $A[j+1\;\ldots \;j]$ .이 작업은 $\max(0,$ ${\displaystyle \max(0,})$ 을 할당하여 6행에서 수행된다.current_sum ${\displaystyle +A[j])$ 의 $+A[j])$ 새로운 값으로 $}$ current_sum, 그 후 $i\in \{1,\ldots ,j+1\}$ $A[i]+\cdots +A[j]$ [ $i\in \{1,\ldots ,j+1\}$ i $i\in \{1,\ldots ,j+1\}$ ] $A[i]+\cdots +A[j]$ + $\{1,\ldots, j+1\}$ 의 합계 $i\in \{1,\ldots ,j+1\}$ $i\in \{1,\ldots ,j+1\}$ [ $A[i]+\cdots +A[j]$ $A[i]+\cdots +A[j]$ + $A[i]+\cdots +A[j]$ + $A[i]+\cdots +A[j]$ + $A[i]+\cdots +A[j]$ $displaystyle A[i]+\cdots +A[j]}$ 에 대해 최대값을 고정한다 $A[i]+\cdots +A[j]$

따라서 이 문제는 여기 파이톤으로 표현된 다음과 같은 코드로 해결할 수 있다.^[4]^[7]

반항하다 max_subarray(숫자):     """"연속적인 하위 배열 중에서 가장 큰 합을 찾아라."""     best_sum = 0     current_sum = 0     을 위해 x 에 숫자:         current_sum = 맥스.(0, current_sum + x)         best_sum = 맥스.(best_sum, current_sum)     돌아오다 best_sum

입력에 양의 요소가 없는 경우(입력이 비어 있는 경우를 포함) 알고리즘의 이 버전은 0으로 반환된다.

빈 하위 검사 승인 없음

빈 하위선을 허용하지 않는 문제의 변형에 대해,best_sum대신^[11] 음의 무한대로 초기화되어야 하며 루프에서도 초기화되어야 함current_sum으로 갱신되어야 한다.max(x, current_sum + x).^{[note 7]} 이 경우 입력에 양소자가 없으면 반환되는 값은 가장 큰 원소(즉, 0에 가장 가까운 값)의 값이고, 입력 내용이 비어 있으면 음의 무한대가 된다.정확성을 위해 입력 어레이가 비어 있을 때 예외를 제기해야 한다. 빈 어레이에는 최대 하위 어레이가 없기 때문이다.

반항하다 max_subarray(숫자):     """"연속적인 하위 배열 중에서 가장 큰 합을 찾아라."""     만일 아닌(숫자):         높이다 ValueError('빈 배열에는 비어 있지 않은 하위 선이 없음')      best_sum = 둥둥 뜨다('-inf')     current_sum = 0     을 위해 x 에 숫자:         current_sum = 맥스.(x, current_sum + x)         best_sum = 맥스.(best_sum, current_sum)     돌아오다 best_sum

조건부로 빈 하위 검사 허용

비어 있는 하위선을 승인할 때 문제가 되는 유일한 경우는 입력 배열의 모든 숫자가 음수인 경우다.이 경우 최대 하위 배열이 비어 있거나(빈 하위 배열이 허용되는 경우) 입력 배열에서 가장 많은 숫자를 포함(빈 하위 배열이 허용되지 않는 경우)한다.

빈 하위선을 허용하는 대체 알고리즘은 위에 주어진 알고리즘에서 쉽게 개발되며, 이 알고리즘은 비어 있는 하위선을 허용하지 않는다.필요한 유일한 변화는 돌아오는 것이다.max(best_sum, 0)대신에best_sum이 버전이 올바르다는 것을 알 수 있다.

빈 입력 배열의 경우 이전 알고리즘이 마이너스 무한으로 반환되므로 이 알고리즘은 0으로 반환되며, 이는 빈 하위 배열의 요소 합계에 해당한다.
음수만 있는 입력 배열의 경우, 이전 알고리즘은 음수인 정수 중 가장 큰 정수를 반환한다.따라서 이 알고리즘은 0을 반환하게 되는데, 이는 빈 하위 배열의 원소의 합에 해당한다.
다른 모든 경우에 대해 출력에는 적어도 하나의 음이 아닌 정수가 있으므로 원소의 합이 0 이상인 비어 있지 않은 하위 배열이 있다.빈 하위선에 대해서는 원소의 합이 항상 0이므로 빈 하위선이 인정되는지 여부는 중요하지 않으므로 이 알고리즘은 이전 알고리즘이 제공하는 것과 동일한 답을 정확하게 반환한다.

또한 이 알고리즘은 다음과 같은 매개변수에 기초하여 조건부로 빈 하위선을 허용하는 버전으로 변환될 수 있다.비어 있는 하위선이 허용되면 반환max(0, best_sum), 그렇지 않으면 반환best_sum입력 배열이 비어 있지만 비어 있는 하위 배열은 허용되지 않는 예외를 제기해야 한다.

반항하다 max_subarray(숫자, accept_message_subarrays=진실의):     """"연속적인 하위 배열 중에서 가장 큰 합을 찾아라."""     만일 아닌(accept_message_subarrays) 그리고 아닌(숫자):         높이다 ValueError('빈 배열에는 비어 있지 않은 하위 선이 없음')      best_sum = 둥둥 뜨다('-inf')     current_sum = 0     을 위해 x 에 숫자:         current_sum = 맥스.(x, current_sum + x)         best_sum = 맥스.(best_sum, current_sum)      만일 accept_message_subarrays:         best_sum = 맥스.(0, best_sum)      돌아오다 best_sum

최고의 서브 어레이의 포지션 계산

알고리즘은 최대 서브 어레이의 시작 및 종료 지수를 추적하도록 수정할 수 있다.

반항하다 max_subarray(숫자):     """"가장 큰 합을 가진 연속적인 하위 배열을 찾아라."""     best_sum = 0  # 또는: floatful-inf')     best_start = best_end = 0  # 또는: 없음     current_sum = 0     을 위해 current_end, x 에 열거하다(숫자):         만일 current_sum <= 0:             # 현재 요소에서 새 시퀀스 시작             current_start = current_end             current_sum = x         다른:             # 현재 요소로 기존 시퀀스 확장             current_sum += x          만일 current_sum > best_sum:             best_sum = current_sum             best_start = current_start             best_end = current_end + 1  # +1은 Python의 슬라이스 컨벤션(endpoint 제외)과 'best_end'를 일치시키는 것이다.      돌아오다 best_sum, best_start, best_end

Python에서 어레이는 0부터 인덱싱되며 슬라이스는 엔드포인트를 제외하므로 어레이 a=[-11, 22, 33, -44]의 하위 어레이 [22, 33]은 a[1:3]로 표현된다.

복잡성

이 알고리즘이 최적의 하위구조물을 사용하는 방법 때문에(각 위치에서 끝나는 최대 하위 배열은 관련되지만 더 작고 중복되는 하위 문제: 이전 위치에서 끝나는 최대 하위 배열) 이 알고리즘은 단순/다양한 동적 프로그래밍의 예로 볼 수 있다.

Kadane $O(n)$ 의 런타임 복잡성은 $O(n)$ ( n $O(n)$ ) $O(n)$ 입니다 $O(n)$ ^[4]^[7]

일반화

고차원 배열에도 유사한 문제가 제기될 수 있지만, 그 해결책은 더 복잡하다. 예를 들어 Takaoka(2002)를 참조하라.Brodal & Jørgensen(2007)은 최적의 시간 경계 $O(n+k)$ + k $){\displaystyle O(n+k)}$ 에서 1차원 배열에서 k 가장 큰 서브 어레이 합계를 찾는 방법을 보여주었다 $O(n+k)$

Maximum sum k-sisjoint 하위 선은 최적 시간 $O(n+k)$ O $O(n+k)$ + $O(n+k)$ ) $O(n+k)$ 로 계산될 수도 있다. $O(n+k)$ ^[12]

참고 항목

부분집합 문제

메모들

^ 누적합계 $S[k]=\sum _{x=1}^{k}A[x]$ [ $S[k]=\sum _{x=1}^{k}A[x]$ $S[k]=\sum _{x=1}^{k}A[x]$ = $S[k]=\sum _{x=1}^{k}A[x]$ ∆ $S[k]=\sum _{x=1}^{k}A[x]$ = $S[k]=\sum _{x=1}^{k}A[x]$ 1 $S[k]=\sum _{x=1}^{k}A[x]$ A $S[k]=\sum _{x=1}^{k}A[x]$ [ $S[k]=\sum _{x=1}^{k}A[x]$ $S[k]=\sum _{x=1}^{k}A[x]$ $S[k]=\sum _{x=1}^{k$ 을(를) 미리 계산한 표를 사용함으로써하위 배열 합계를 $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ 하는 $S[k]=\sum _{x=1}^{k}A[x]$ $A$ $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ $x]}$ = $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ A $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ [ $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ = $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ [ $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ - $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ [ $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ - $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ $\sum _{x=i}^{j$ $일정한$ 시간 $내$ 에 A $[x]=S[j]-S[$ i-1 $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ ]}
^ 모든 알고리즘은 적어도 한 번 어레이를 스캔해야 하므로 이미 O(n) 시간이 소요됨
^ 이름 지어진MaxEndingHere벤틀리 (1989년)에서cGries (1982)에서
^ 이름 지어진MaxSoFar벤틀리 (1989년)에서sGries (1982)에서
^ $i=j$ 합은 i $i=j$ = $i=j$ {\ $displaystyle$ i $=j}$ 일 $0$ 때 $0$ 이며 $i=j$ 이는 빈 하위 배열 $A[j\ldots j-1]$ [ $A[j\ldots j-1]$ … $A[j\ldots j-1]$ - $A[j\ldots j-1]$ $A[j\ldots j-1]$ $A[j\ldots j-1]$ 에 해당한다 $A[j\ldots j-1]$
^ 아래의 Python 코드에서 $A[j]$ [ $A[j]$ $A[j]$ $A[j]$ 은(는) 다음과 같이 표현된다 $A[j]$ .x인덱스 $j$ $j$ 을(를) 암시적으로 남겨둔 $j$ 상태로.
^ 후자 수정은 벤틀리(1989년)에 의해 언급되지 않지만, 수정된 루프 불변성을 유지한다.current_sum ${\displaystyle =\max _{1$ $j$ $j$ 단계 $j$ 시작 $=\max _{i\in \{1,...,j\}}A[i]+...+A[j]$ 부분에 + $A[j]}$

참조

^ 벤틀리 1989, 페이지 69.
^ 벤틀리 1989, 페이지 70.
^ 벤틀리 1989, 페이지 73.
^ ^a ^b ^c 벤틀리 1989, 페이지 74.
^ ^a ^b 벤틀리 1984, 페이지 868-869.
^ 벤틀리 1989, 76-77페이지.
^ ^a ^b ^c Gries 1982, 페이지 211.
^ Gries 1982, 페이지 209-211.
^ 버드 1989, 8장 126쪽
^ 백쿠르스, 디칼라 & 짜모스 2016.
^ 벤틀리 1989, 78,171페이지.
^ 벵츠슨 & 첸 2007.

Backurs, Arturs; Dikkala, Nishanth; Tzamos, Christos (2016), "Tight Hardness Results for Maximum Weight Rectangles", Proc. 43rd International Colloquium on Automata, Languages, and Programming: 81:1–81:13, doi:10.4230/LIPIcs.ICALP.2016.81, S2CID 12720136
Bae, Sung Eun (2007), Sequential and Parallel Algorithms for the Generalized Maximum Subarray Problem (PDF) (Ph.D. thesis), University of Canterbury, S2CID 2681670, archived from the original (PDF) on 2017-10-26.
Bengtsson, Fredrik; Chen, Jingsen (2007), Computing maximum-scoring segments optimally (PDF) (Research report), Luleå University of Technology
Bentley, Jon (1984), "Programming Pearls: Algorithm Design Techniques", Communications of the ACM, 27 (9): 865–873, doi:10.1145/358234.381162, S2CID 207565329
Bentley, Jon (May 1989), Programming Pearls (2nd? ed.), Reading, MA: Addison Wesley, ISBN 0-201-10331-1
Bird, Richard S. (1989), "Algebraic Identities for Program Calculation" (PDF), The Computer Journal, 32 (2): 122–126, doi:10.1093/comjnl/32.2.122^{[데드링크]}
Brodal, Gerth Stølting; Jørgensen, Allan Grønlund (2007), "A linear time algorithm for the k maximal sums problem", Mathematical Foundations of Computer Science, Lecture Notes in Computer Science, vol. 4708, Springer-Verlag, pp. 442–453, doi:10.1007/978-3-540-74456-6_40.
Gries, David (1982), "A Note on the Standard Strategy for Developing Loop Invariants and Loops" (PDF), Science of Computer Programming, 2 (3): 207–241, doi:10.1016/0167-6423(83)90015-1, hdl:1813/6370
Takaoka, Tadao (2002), "Efficient algorithms for the maximum subarray problem by distance matrix multiplication", Electronic Notes in Theoretical Computer Science, 61: 191–200, doi:10.1016/S1571-0661(04)00313-5.
Tamaki, Hisao; Tokuyama, Takeshi (1998), "Algorithms for the Maximum Subarray Problem Based on Matrix Multiplication", Proceedings of the 9th Symposium on Discrete Algorithms (SODA): 446–452, retrieved November 17, 2018

외부 링크

TAN, Lirong. "Maximum Contiguous Subarray Sum Problems" (PDF). Archived from the original (PDF) on 2015-10-10. Retrieved 2017-10-26.
Mu, Shin-Cheng (2010). "The Maximum Segment Sum Problem: Its Origin, and a Derivation".
"Notes on Maximum Subarray Problem". 2012.
www.algorithmist.com
알렉세이고르wikidot.com
로제타 코드의 최대 부수적 합계 문제
카다네 알고리즘의 괴짜들 페이지

[6] 누적합계 $S[k]=\sum _{x=1}^{k}A[x]$ [ $S[k]=\sum _{x=1}^{k}A[x]$ $S[k]=\sum _{x=1}^{k}A[x]$ = $S[k]=\sum _{x=1}^{k}A[x]$ ∆ $S[k]=\sum _{x=1}^{k}A[x]$ = $S[k]=\sum _{x=1}^{k}A[x]$ 1 $S[k]=\sum _{x=1}^{k}A[x]$ A $S[k]=\sum _{x=1}^{k}A[x]$ [ $S[k]=\sum _{x=1}^{k}A[x]$ $S[k]=\sum _{x=1}^{k}A[x]$ $S[k]=\sum _{x=1}^{k$ 을(를) 미리 계산한 표를 사용함으로써하위 배열 합계를 $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ 하는 $S[k]=\sum _{x=1}^{k}A[x]$ $A$ $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ $x]}$ = $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ A $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ [ $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ = $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ [ $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ - $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ [ $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ - $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ $\sum _{x=i}^{j$ $일정한$ 시간 $내$ 에 A $[x]=S[j]-S[$ i-1 $\sum _{x=i}^{j}A[x]=S[j]-S[i-1]$ ]}

[9] 모든 알고리즘은 적어도 한 번 어레이를 스캔해야 하므로 이미 O(n) 시간이 소요됨

[13] 이름 지어진MaxEndingHere벤틀리 (1989년)에서cGries (1982)에서

[14] 이름 지어진MaxSoFar벤틀리 (1989년)에서sGries (1982)에서

[15] $i=j$ 합은 i $i=j$ = $i=j$ {\ $displaystyle$ i $=j}$ 일 $0$ 때 $0$ 이며 $i=j$ 이는 빈 하위 배열 $A[j\ldots j-1]$ [ $A[j\ldots j-1]$ … $A[j\ldots j-1]$ - $A[j\ldots j-1]$ $A[j\ldots j-1]$ $A[j\ldots j-1]$ 에 해당한다 $A[j\ldots j-1]$

[16] 아래의 Python 코드에서 $A[j]$ [ $A[j]$ $A[j]$ $A[j]$ 은(는) 다음과 같이 표현된다 $A[j]$ .x인덱스 $j$ $j$ 을(를) 암시적으로 남겨둔 $j$ 상태로.

[18] 후자 수정은 벤틀리(1989년)에 의해 언급되지 않지만, 수정된 루프 불변성을 유지한다.current_sum ${\displaystyle =\max _{1$ $j$ $j$ 단계 $j$ 시작 $=\max _{i\in \{1,...,j\}}A[i]+...+A[j]$ 부분에 + $A[j]}$

[FOOTNOTEBentley198969-1] 벤틀리 1989, 페이지 69.

[FOOTNOTEBentley198970-2] 벤틀리 1989, 페이지 70.

[FOOTNOTEBentley198973-3] 벤틀리 1989, 페이지 73.

[FOOTNOTEBentley198974-4] 벤틀리 1989, 페이지 74.

[FOOTNOTEBentley1984868-869-5] 벤틀리 1984, 페이지 868-869.

[FOOTNOTEBentley198976-77-7] 벤틀리 1989, 76-77페이지.

[FOOTNOTEGries1982211-8] Gries 1982, 페이지 211.

[FOOTNOTEGries1982209-211-10] Gries 1982, 페이지 209-211.

[FOOTNOTEBird1989Sect.8,_p.126-11] 버드 1989, 8장 126쪽

[FOOTNOTEBackursDikkalaTzamos2016-12] 백쿠르스, 디칼라 & 짜모스 2016.

[FOOTNOTEBentley198978,171-17] 벤틀리 1989, 78,171페이지.

[FOOTNOTEBengtssonChen2007-19] 벵츠슨 & 첸 2007.

[1]

[2]

[3]

[4]

[5]

[note 1]

[6]

[7]

[note 2]

[8]

[9]

[10]

[note 3]

[note 4]

[note 5]

[11]

[note 7]

[12]

Search