클라인 역설

이 글은 물리학 전문가의 주의가 필요하다. 구체적인 문제는 다음과 같다. 여기에 제시된 도표와 해석은 확인이 필요하다. 위키프로젝트물리학(Wiki Project Physics)이 전문가 영입을 도울 수 있을 것이다(2019년 10월)

물리학자인 오스카 클라인은^[1] 1929년 잠재적 장벽에서 전자 산란이라는 익숙한 문제에 디락 방정식을 적용해 놀라운 결과를 얻었다. 비상대적 양자역학에서는 전자 터널링을 방벽으로 관측하며, 지수적 감쇠가 있다. 그러나 클라인의 결과는 잠재력이 전자 질량 $V{\displaystyle }$~ m ${\displaystyle c}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$인 경우$$장벽이 거의 투명하다는 것을 보여주었다. 더구나 전위가 무한대에 가까워질수록 반사는 줄어들고 전자는 항상 전달된다.

그 역설의 즉각적인 적용은 중성자가 발견되기 전, 핵 내의 중성입자에 대한 러더포드의 양성자-전자 모델에 대한 것이었다. 그 역설은 핵 안에 갇힌 전자의 개념에 양자역학적으로 반대했다.^[2] 이 명확하고 정확한 역설은 전자가 어떤 전위 우물에 의해서도 핵 안에 갇힐 수 없다는 것을 암시했다. 이 역설의 의미는 당시 치열하게 논의되었다.^[2]

질량이 없는 입자

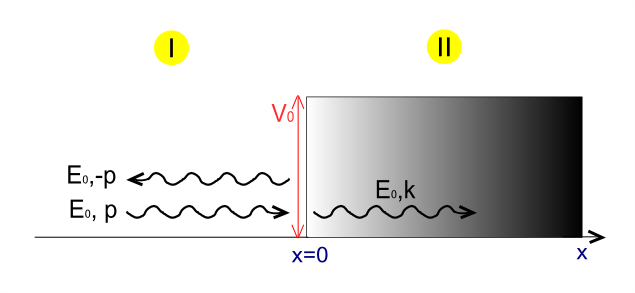
$에너지{\displaystyle {}_{}}$ < > ${\$ 및 모멘텀 $p{\displaystyle }$ ${\displaystyle p}$의 잠재적 단계에 접근하는 질량 없는 상대론적 입자를 고려하십시오$.$

입자의 파동 $함수$인 , ${\displaystyle \psi }$은 시간 독립적인$$Dirac 방정식을 따른다.

${\displaystyle \left(\sigma _{x}p+V\right)\psi =E_{0}\psi,\quad V={\begin{case}0,&x<0\\\\\)V_{0},&x>0\end{case}}$

그리고 $\sigma {\displaystyle {}_{}}$ ${\displaystyle x_{}}$ ${\$는 Pauli 행렬이다.

${\displaystyle \putma _{x}=\left\ft}{ft}0&1\\1&0\end{ft}\오른쪽)}$

입자가 왼쪽에서 전파된다고 가정할 때 우리는 두 가지 해결책을 얻는데, 하나는 단계 전, 하나는 지역 (1)에서 그리고 다른 하나는 잠재력 (2)에서 얻는다.

${\displaystyle \psi _{1}=Ae^{ipx}\왼쪽({\begin{matrix}1\\1\end{matrix}\오른쪽)++A'e^{-ipx}\왼쪽({\begin{matrix}-1\\1\end{matrix}\오른쪽),\quad p=E_{0}\,}$

${\displaystyle \psi _{2}=Be^{ikx}\좌측({\begin{matrix}1\\1\end{matrix}\우측)\quad \좌측 k\우측 =V_-E_{0},},},}$

여기서 계수 A, A′, B는 복잡한 숫자다. 수신 및 송신파 함수는 모두 양의 그룹 속도(그림 1의 파란색 선)와 연관되어 있는 반면, 반사파 함수는 음의 그룹 속도와 연관되어 있다. (그림 1의 녹색 선)

이제 전송 및 반사 계수 $T{\displaystyle }$, ${\displaystyle R}$. ${\displaystyle T, R.}$을(를) 계산하려고 한다. 이 계수들은 확률 진폭 전류에서 파생된다.

Dirac 방정식과 관련된 확률 전류의 정의는 다음과 같다.

${\displaystyle J_{i}=\psi _{i}^{\dager }\sigma _{x}\psi _{i}\i=1,2\,}$

이 경우:

${\displaystyle J_{1}=2\좌측[\좌측 A\우측 ^{2}-\좌측 A'\우측 ^{2}\우측]\quad J_{2}=2\좌측 B\우측 ^{2},}$

전달 및 반사 계수는 다음과 같다.

${\displaystyle R={\frac {\좌측 A'\우측 ^{2}}:{\좌측 A\우측 ^{2}}:},\쿼드 T={\frac {\좌측 B\우측 ^{2}}:{\좌측 A\우측 ^{1},},},}$

$x{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle x=0$에서 파형 함수의 연속성:

${\displaystyle \왼쪽 A\오른쪽 ^{2}=\왼쪽 B\오른쪽 ^{2}\,}$

${\displaystyle \왼쪽 A'\오른쪽 ^{2}=0\,}$

그래서 전송 계수는 1이고 반사되는 것은 없다.

역설의 한 가지 해석은 잠재적 단계가 질량이 없는 상대론 입자의 집단 속도의 방향을 되돌릴 수 없다는 것이다. 이 설명은 위에 인용한 단일 입자 용액에 가장 적합하다. 그 밖의 문헌에서는 입자-항문자 쌍의 전위성으로 인해 구속되지 않은 튜닝이 발생하는 것으로 보이는 양자장 이론의 맥락에서 보다 복잡한 해석을 제시한다.

매시브 케이스

이 구간은 확장이 필요하다. 더하면 도움이 된다.(2018년 5월)

대규모 사례의 경우, 계산은 위와 유사하다. 그 결과는 질량이 없는 경우만큼이나 놀랍다. 전송 계수는 항상 0보다 크며, 전위 단계가 무한대로 갈 때 1에 접근한다.

클라인 존

입자의 에너지가 < < V- ${\displaystyle m<E>V-m}$범위에 있으면 전체 반사보다는 부분 반사가 발생한다.

대규모 사건 해결책

전통적인 분해능은 양자장 이론(Hansen 1981년)의 맥락에서 입자/반입자 쌍 생성을 사용하지만, 물리적 쌍 생성을 장벽 아래 음의 에너지 해결책의 산란을 대체하는 단순한 분해능이 존재한다(Alhaidari 2009년). 이 전략은 무한정 사각형의 우물용 디락 방정식에 대한 분석적 해결책을 얻기 위해서도 적용되었다.

기타경우수

이러한 결과는 더 높은 차원으로 확장되었고, 선형 계단, 사각 장벽, 부드러운 전위 등과 같은 다른 유형의 전위로 확장되었다. 그래핀의 전자 운송에 관한 많은 실험들은 질량이 없는 입자에 대해 클라인 역설에 의존한다.^[3][4]

참고 항목

• 역설의 목록

참조

추가 읽기

• Dombey, N; Calogeracos, A. (July 1999). "Seventy years of the Klein paradox". Physics Reports. 315 (1–3): 41–58. Bibcode:1999PhR...315...41D. doi:10.1016/S0370-1573(99)00023-X.
• Robinson, T. R. (2012). "On Klein tunneling in graphene". American Journal of Physics. 80 (2): 141–147. Bibcode:2012AmJPh..80..141R. doi:10.1119/1.3658629.
• Calogeracos, A.; Dombey, N. (1999). "History and physics of the Klein paradox". Contemporary Physics. 40 (5): 313. arXiv:quant-ph/9905076. Bibcode:1999ConPh..40..313C. doi:10.1080/001075199181387.