궤도 공명

Orbital resonance
공상과학 소설에 대해서는 궤도 공명(소설)을 참고하세요.
목성의 갈릴레이 위성 3개가 보여준 3체 라플라스 공명.연결은 짧은 색상 변화로 강조됩니다.각 유로파-가니메데 접속(마젠타)에는 2개의 유로파 접속(녹색)과 3개의 유로파-가니메데 접속(회색)이 있습니다.이 도표는 축척하지 않습니다.

천체역학에서 궤도공명은 궤도를 도는 물체들이 주기적이고 주기적인 중력을 서로 작용할 때 발생하는데, 이는 궤도 주기가 작은 정수들의 비율에 의해 연관되기 때문입니다.가장 일반적으로, 이 관계는 한 쌍의 물체(이진공명) 사이에서 발견됩니다.궤도 공명 뒤에 있는 물리적 원리는 어린이를 그네에 밀어 넣는 것과 개념이 비슷하여, 궤도와 그네는 모두 고유 진동수를 가지며, "밀어내는" 몸은 주기적인 반복으로 작용하여 운동에 누적적인 영향을 미칩니다.궤도 공명은 물체의 상호 중력 영향력을 크게 강화합니다. (즉, 서로의 궤도를 변경하거나 제약하는 능력).대부분의 경우, 이것은 불안정한 상호작용으로 이어지는데, 이것은 물체가 운동량을 교환하고 공명이 더 이상 존재하지 않을 때까지 궤도를 이동하는 것입니다.어떤 상황에서는 공진 시스템이 자체적으로 보정되어 안정적일 수 있습니다.목성의 위성 가니메데, 유로파, 이오의 1:2:4 공명과 해왕성과 명왕성의 2:3 공명이 그 예입니다.토성의 내부 위성과의 불안정한 공명은 토성 고리에 틈을 일으킵니다.궤도 반경이 비슷한 물체들 사이의 1:1 공명이라는 특별한 경우는 큰 행성계 물체들이 궤도를 공유하는 대부분의 다른 물체들을 분출하게 합니다. 이는 현재 [1]행성의 정의에 사용되는 효과인 이웃을 제거하는 훨씬 더 광범위한 과정의 일부입니다.

이 글에서 이진공진비는 같은 시간 간격으로 완료된 궤도의 수를 역비로 해석하는 것이 아니라 그 수를 역비로 해석해야 합니다.따라서 위의 2:3 비율은 명왕성이 해왕성이 3개의 궤도를 완성하는 데 걸리는 시간 내에 2개의 궤도를 완성한다는 것을 의미합니다.세 개 이상의 물체 사이의 공진 관계의 경우, 두 가지 유형의 비율 중 하나를 사용할 수 있으며(가장 작은 전체 정수 비율 시퀀스가 반드시 서로 반전되는 것은 아님), 비율의 유형이 지정됩니다.

역사

17세기에 뉴턴의 만유인력 법칙이 발견된 이후, 태양계의 안정성은 피에르시몽 라플라스를 시작으로 많은 수학자들을 사로잡았습니다.2체 근사에서 발생하는 안정 궤도는 다른 물체의 영향을 무시합니다.이러한 추가적인 상호작용이 태양계의 안정성에 미치는 영향은 매우 적지만, 처음에는 궤도의 매개변수를 크게 변화시키고 완전히 다른 구성으로 이어질 수 있는지 여부는 알 수 없었습니다.또는 다른 안정화 효과가 행성의 궤도의 구성을 유지할 수 있는지 여부.

갈릴레이 위성들의 연결된 궤도를 설명하는 첫 번째 답을 찾은 사람은 라플라스였습니다.뉴턴 이전에는 궤도 운동의 비율과 비율에 대한 고려도 있었는데, 이를 "구(球)의 음악", 즉 보편적인 음악(musica universalis)이라고 불렀습니다.

공명 상호작용에 관한 기사는 일반적인 현대 환경에서의 공명을 설명합니다.동적 시스템 연구의 주요 결과는 모드 잠금의 매우 단순화된 모델을 발견하고 설명하는 것입니다. 이 모델은 일부 구동 모터에 대한 약한 결합을 통해 주기적인 킥을 수신하는 오실레이터입니다.여기서 유사한 것은 더 무거운 물체가 지나갈 때 더 작은 물체에 주기적인 중력 발차기를 제공한다는 것입니다.모드 잠금 지역은 아놀드 혀(Arnold tongues)라고 불립니다.

공명의 종류

해왕성과 낮은 정수 공명 위치에 있는 해왕성(위쪽 근처의 수직 적색 막대)과의 반주축이 모여 있는 것과 대조적으로, 세제곱와노스(파란색) 및 비공진(또는 공명하지 않는) 산란 물체(회색)의 위치에 있습니다.
목성과의 공명으로 궤도가 불안정한 커크우드 간극을 보여주는 소행성 반장축 분포도
토성의 A 고리에 있는 나선형 밀도의 파동은 내달과의 공명으로 인해 흥분합니다.이러한 파동은 행성에서 (왼쪽 위를 향해) 전파됩니다.중심 바로 아래에 있는 큰 파도들은 야누스와의 6:5 공명 때문입니다.
토성 C 고리의 컬럼보 갭(가운데)에 있는 편심 타이탄 링렛과[2] 그 바로 안쪽의 굽힘파에서[3][4] 공명하는 입자들의 경사진 궤도는 각각 타이탄의 평균운동에 상응하는 압시달과 결절점을 가지고 있습니다.

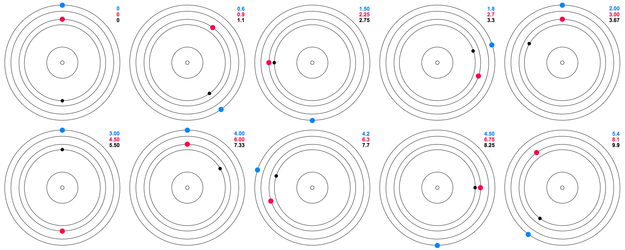
일반적으로 궤도 공명은

  • 궤도 매개변수(예: 이심률 대 반장축 또는 이심률 대 경사)의 하나 또는 임의의 조합을 포함합니다.
  • 궤도 주기로 측정할 수 있는 단기에서 10년에서6 10년 후에4 측정되는 세속적인 것에 이르기까지 모든 시간 척도로 행동합니다.
  • 궤도의 장기적인 안정화를 초래하거나 궤도의 불안정화의 원인이 될 수 있습니다.

평균운동 궤도 공명은 두 물체가 서로의 단순한 정수비인 공전 주기를 가질 때 발생합니다.세부 사항에 따라, 이것은 궤도를 안정화시키거나 불안정하게 만들 수도 있습니다.안정화는 두 물체가 결코 가까이 접근하지 않을 정도로 동기화된 방식으로 움직일 때 발생할 수 있습니다.예를 들어 다음과 같습니다.

  • 명왕성과 명왕성의 궤도는 훨씬 큰 해왕성의 궤도를 가로지르지만 안정적인데, 이는 명왕성과 2:3 공명을 하기 때문입니다.이 공명은 해왕성이 근일점과 해왕성의 궤도에 접근할 때 해왕성이 (궤도의 4분의 1을 평균하여) 지속적으로 멀리 떨어져 있음을 보장합니다.공명 상태에 있지 않은 다른 (훨씬 더 많은) 해왕성 횡단 천체들은 해왕성으로 인한 강한 섭동에 의해 그 지역에서 분출되었습니다.또한 해왕성에 대한 1:1 (해왕성 트로이목마), 3:5, 4:7, 1:2 (두 개의 티노) 및 2:5 공명을 차지하는 넵튠 횡단 물체의 작지만 중요한 그룹이 있습니다.
  • 태양으로부터 3.5 천문단위 이상 떨어진 소행성대에서는 목성과 3:2, 4:3, 1:1 공명을 이루는 소행성들이 모여 있습니다.

궤도 공명은 궤도 중 하나를 불안정하게 만들 수도 있습니다.이 과정은 에너지 효율적인 우주선 [5][6]궤도 이탈 방법을 찾기 위해 활용될 수 있습니다.작은 몸의 경우 불안정해질 가능성이 훨씬 높습니다.예를 들어 다음과 같습니다.

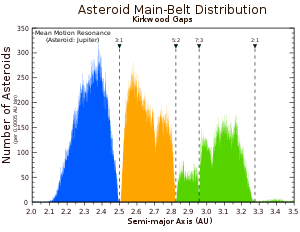
  • 태양으로부터 3.5 AU 이내에 있는 소행성대에서 목성과의 주요 평균운동 공명은 소행성 분포의 틈, 커크우드 간극(가장 눈에 띄는 것은 4:1, 3:1, 5:2, 7:3, 2:1 공명)의 위치입니다.소행성들은 반복적인 섭동에 의해 거의 텅 빈 차선에서 쫓겨났습니다.하지만, 아직도 이러한 공명 속에 또는 그 근처에 일시적으로 존재하는 소행성의 개체수가 있습니다.예를 들어, 알린다족의 소행성들은 3:1 공명 안에 있거나 가까이 있으며, 궤도 이심률은 목성과의 상호작용에 의해 꾸준히 증가하여 결국 공명으로부터 자신들을 방출하는 내행성과 가까이 조우하게 됩니다.
  • 토성의 고리에서 카시니 분할은 달 미마스와 2:1 공명으로 제거된 안쪽 B 고리와 바깥쪽 A 고리 사이의 간격입니다. (구체적으로, 공명이 일어나는 곳은 B 고리의 바깥쪽 가장자리를 경계로 하는 호이겐스 간극입니다.)
  • 토성의 고리에서, A 고리 내의 엥케와 킬러 간격은 각각 달이 박힌 판과 다프니스와의 1:1 공명에 의해 제거됩니다.A 고리의 바깥쪽 가장자리는 달 야누스와의 불안정한 7:6 공명에 의해 유지됩니다.

공명 궤도에 있는 대부분의 물체들은 같은 방향이지만, 역행 소행성 514107 카에파오카엘라는 [7]목성과 (최소 백만 년 동안) 안정적인 1:1 공명을 하고 있는 것으로 보입니다.게다가, 목성이나 [8]토성과의 평균 운동 공명에서 일시적으로 포착되는 몇 개의 역행 다모클로이드가 발견되었습니다.그러한 궤도 상호작용은 같은 [8][9]방향으로 궤도를 도는 물체들 사이의 상응하는 상호작용보다 약합니다.해왕성 횡단 천체 201119 KT는 행성들의 궤도면에 대해 110°의 궤도 경사를 가지고 있으며 현재 [10]해왕성과 7:9 극 공명 중에 있습니다.

라플라스 공명(Laplace resonance)은 궤도 주기 비율이 1:2:4인 삼체 공명을 말합니다.이 용어는 피에르-시몽 라플라스가 그러한 공명이 목성의 위성 이오, 유로파, 가니메데의 움직임을 조절한다는 것을 발견했기 때문에 생겨났습니다.현재 글리제 876 c, b, [12][13][14]e와 같은 [11]비율의 다른 3체 공명에도 적용되는 경우가 많습니다.다른 단순한 정수 비율을 포함하는 3체 공명은 "라플라스형"[15] 또는 "라플라스형"[16]이라고 불립니다.

린드블라드 공명은 은하와 (별들이 나선팔 자체에 의해 힘을 받게 되는) 토성의 고리(고리 입자들이 토성의 위성에 의해 힘을 받게 되는) 둘 다에서 나선 밀도파를 구동합니다.

세속적 공명은 두 궤도의 세차운동이 동기화될 때 발생합니다(일반적으로 근일점이나 상승점의 세차운동).세속적 공명을 하는 작은 물체와 훨씬 큰 물체(예: 행성)는 큰 물체와 같은 속도로 진행할 것입니다.오랜 시간에 걸쳐(100만 년 정도) 세속적인 공명은 작은 몸의 편심과 성향을 변화시킬 것입니다.

세속적인 공명의 몇몇 두드러진 예로는 토성이 있습니다.토성의 자전축의 세차운동과 해왕성의 공전축의 세차운동 사이에는 거의 공명이 있으며, 이는 토성의 큰 축 기울기(26.7°)[17][18][19]의 가능성이 있는 원천으로 확인되었습니다.처음에 토성은 목성의 기울기(3.1°)에 가까웠을 것입니다.카이퍼대의 점진적인 고갈은 해왕성 궤도의 세차운동 속도를 감소시켰을 것입니다. 결국 주파수가 일치했고, 토성의 축 세차운동은 스핀 궤도 공명으로 포착되어 토성의 경사도가 증가했습니다.(해왕성 궤도의 각운동량은 토성의 자전속도의 10배이며4, 따라서 상호작용을 지배합니다.)그러나 공명은 더 이상 존재하지 않는 것 같습니다.카시니 우주선의 데이터를 자세히 분석하면 공명이 존재할 수 있는 범위를 조금 벗어난 토성의 관성 모멘트 값을 얻을 수 있는데, 이는 스핀 축이 과거에 그랬던 것처럼 장기적으로 해왕성의 궤도 경사와 같은 위상을 유지하지 않는다는 것을 의미합니다.공명이 왜 끝나게 되었는지에 대한 한 가지 이론은 토성 주변에 약 1억년 전에 궤도가 불안정해져 [20][21]토성을 휘젓고 다녔던 또 다른 달이 있었다는 것입니다.

소행성과 토성 사이의 근일점 세속적인 공명(지름 = g - g)은 소행성대를 형성하는 데 도움이 됩니다(첨자 "6"은 토성을 태양으로부터 6번째 행성으로 나타냄).이 행성에 접근하는 소행성들은 화성을 횡단할 때까지 서서히 이심률이 증가하며, 이때 보통 화성으로 근접 통과하여 소행성대에서 방출됩니다.이 공명은 약 20°의 경사에서 2 AU 부근에서 소행성대의 안쪽과 "측면" 경계를 형성합니다.

수치 시뮬레이션에 따르면 수성과 목성 사이의 근일점 세속 공명(g = g)의 궁극적인 형성은 수성의 이심률을 크게 증가시키고 지금으로부터 수십억 년 후에 태양계 내부를 불안정하게 만들 가능성이 있습니다.

토성의 C 고리 안에 있는 타이탄 고리는 한 궤도의 압시달 세차운동 속도가 다른 궤도의 공전 속도와 정확히 일치하는 또 다른 형태의 공명을 나타냅니다.이 별난 고리의 바깥쪽 끝은 항상 토성의 주요 위성 [2]타이탄을 향하고 있습니다.

코자이 공명은 교란된 궤도의 기울기와 이심률이 동시에 진동할 때 발생합니다(기심률은 증가하지만 기울기는 감소합니다).이 공명은 고도로 기울어진 궤도에 있는 물체에만 적용됩니다. 결과적으로 이러한 궤도는 불안정한 경향이 있는데, 이심률이 커지면 작은 심점이 생겨 일반적으로 조석력에 의한 충돌이나 (큰 위성의 경우) 파괴로 이어지기 때문입니다.

궤도 이심률과 관련된 또 다른 형태의 공명의 예에서 가니메데와 칼리스토의 이심률은 181년이라는 공통 주기를 가지고 있지만 서로 반대 [24]위상을 가지고 있습니다.

태양계에서의 평균운동 공명

해왕성(오른쪽 아래 푸른 점)이 정지해 있는 상태에서 회전하는 틀에서 하우메아가 해왕성과 공명한 것으로 추정되는 7:12 묘사.해왕성에 대한 하우메아의 이동 궤도 정렬은 주기적으로 역행하여 공명을 유지합니다.

태양계에는 행성, 왜행성 또는 더 큰 위성을 포함하는 몇 개의 알려진 평균운동공명(MMR)만이 존재합니다(많은 가능성 있는 왜행성을 포함하여 소행성, 행성 고리, 달 착륙선 및 카이퍼 벨트의 더 작은 천체들이 포함됩니다).

또한 하우메아는 [25][26]해왕성과 7:12 공명을 하고, 공공은 [27]해왕성과 3:10 공명을 하고 있다고 생각합니다.

기간 간의 단순한 정수 비율은 더 복잡한 관계를 숨깁니다.

  • 접속점은 공명에 의해 정의된 평형점 주위에서 진동(진동)할 수 있습니다.
  • 0이 아닌 편심이 주어지면, 노드 또는 주변부는 드리프트(공진과 관련된, 짧은 기간, 세속적인 세차운동이 아닌)할 수 있습니다.

후자의 예로 잘 알려진 이오-유로파의 2:1 공명을 생각해 보십시오.공전 주기가 이 관계에 있다면, 평균 n {\ n주기의 역, 종종 하루의 도로 표현됨)은 다음을 만족할 것입니다.

(위키피디아에서) 데이터를 대입하면 -0.7395°일이−1 되며, 이 값은 0과 실질적으로 다릅니다.

사실 공명은 완벽하지만, 근일점(목성에 가장 가까운 지점),ω 의 세차운동도 포함되어 있습니다.정확한 방정식(라플라스 방정식의 일부)은 다음과 같습니다.

다시 말해, Io의 평균 운동은 페리조브의 세차운동을 고려한 Europa의 평균 운동의 두 배입니다.(떠다니는) 주변부에 앉아 있는 관찰자는 달들이 같은 장소에서 서로 결합하는 것을 보게 될 것입니다.위에 나열된 다른 쌍들은 미마스-테티스 공명을 제외하고 동일한 유형의 방정식을 만족합니다.이 경우, 공명은 다음을 만족합니다.

접속점은 두 달의 마디 사이의 중간점 주위에 위치합니다.

라플라스 공명

Io-Europa-Ganymede 공명 그림중앙에서 바깥쪽으로: 이오(노란색), 유로파(회색), 가니메데(어두움)

Io-Europa-Ganymede와 관련된 라플라스 공명은 달의 궤도상을 잠그는 다음과 같은 관계를 포함합니다.

여기서 λ\lates는 달의 평균 길이입니다(두 번째 등호는 자유도를 무시함).

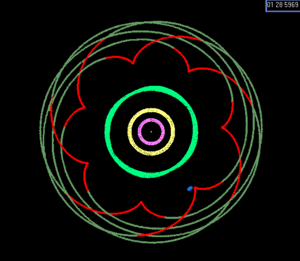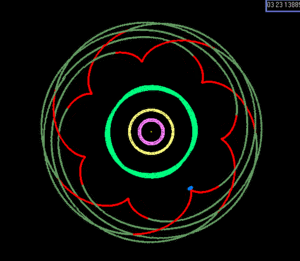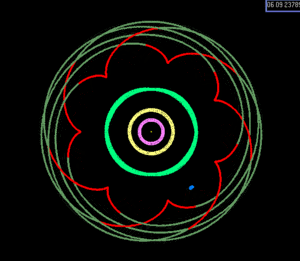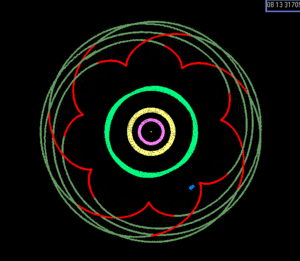
이 관계는 삼중 결합을 불가능하게 만듭니다. (반대로 글리제 876 계의 라플라스 공명은 가장 바깥 행성의 궤도 당 하나의 삼중 결합과 관련되어 있고, 자유도는 무시됩니다.)그래프는 1, 2, 3 Io 주기 후의 달의 위치를 보여줍니다. \L은(는) 진폭이 0.[28]03°인 약 180°의 라이브러리를 합니다.

또 다른 "라플라스" 공명은 [15]명왕성의 위성 스틱스, 닉스, 히드라를 포함합니다.

이는 스틱스, 닉스, 히드라의 궤도 주기를 각각 18:22:33 (또는 카론 주기와의 근공명으로 볼 때, 3+3/11:4:6; 아래 참조)에 가까운 궤도 주기를 반영합니다; 각각의 궤도의 비율은 11:9:6입니다.시노딕 구간의 비율에 따라 Styx와 Hydra의 결합은 5개이고 Styx와 Hydra의 결합은 2개마다 3개의 스틱스와 [15][29]히드라의 결합은 3개입니다.갈릴레이 위성 공명과 마찬가지로 삼중 결합은 금지되어 있습니다.displaystyle \은(는) 진폭이 최소 10°[15]인 약 180°의 라이브러리를 합니다.

공명 주기의 1/3에 걸쳐 히드라(파란색), 닉스(빨간색), 스틱스(검은색)의 연결 순서.움직임은 시계 반대 방향이며 완료된 궤도는 다이어그램의 오른쪽 상단에 집계됩니다(전체 주기를 보려면 이미지를 클릭하십시오).

플루티노 공명

왜행성 명왕성은 해왕성과 공명하는 그물에 갇힌 궤도를 따라가고 있습니다.공명은 다음과 같습니다.

  • 평균운동공진 2:3
  • 근일점의 공명(90° 부근의 회전), 근일점을 황도 위에 유지하는 것
  • 해왕성의 그것과 관련된 근일점의 경도의 공명

이러한 공명의 한 가지 결과는 명왕성이 해왕성의 궤도를 가로지를 때 최소 30 AU의 거리가 유지된다는 것입니다.전체적으로 두 천체 사이의 최소 거리는 17 AU인 반면, 명왕성과 천왕성 사이의 최소 거리는 11[30] AU에 불과합니다(자세한 설명과 그래프는 명왕성의 궤도 참조).

해왕성과 비슷한 2:3 공명에서 플루티노라고 불리는 그 다음으로 큰 천체는 아마도 왜행성 오르쿠스일 것입니다.오르쿠스는 명왕성의 궤도와 비슷한 기울기와 이심률을 가지고 있습니다.그러나 둘은 해왕성과의 상호 공명에 의해 항상 궤도의 반대 위상에 있도록 제약을 받습니다. 따라서 오르쿠스는 때때로 "반-플루토"[31]로 묘사됩니다.

해왕성의 위성 나이아드(궤도 운동이 빨간색으로 표시됨)와 탈라사 사이의 공명을 후자와 공회전하는 관점으로 묘사

Naiad:Thalassa 73:69 공명

해왕성의 가장 안쪽에 있는 달 나이아드는 다음 바깥쪽의 달 탈라사와 73:69 4차 공명을 하고 있습니다.해왕성의 궤도를 돌 때, 더 기울어진 나이아드는 탈라사를 위에서 두 번, 그리고 아래에서 두 번 연속적으로 통과하며, 지구의 ~21.5일 주기로 반복됩니다.두 위성은 서로 지나갈 때 약 3540 km 떨어져 있습니다.그들의 궤도 반경은 1850 km 밖에 차이가 나지 않지만, 나이아드는 탈라사의 궤도면 위 또는 아래에서 가장 가까이에서 약 2800 km를 회전합니다.일반적인 것처럼, 이 공명은 결합에서 분리를 최대화함으로써 궤도를 안정화시키지만, 이심률이 [32][33][note 1]최소인 경우에 궤도 경사가 이러한 회피를 촉진하는 역할을 하는 것은 이례적입니다.

외계 행성들 사이의 평균 운동 공명

궤도비 1:2인 두 행성의 공명 행성계

발견된 대부분의 외계 행성계는 평균 운동 공명을 하는 행성이 발견되지 않았지만, 최대 5개의 공명하는[35] 행성과 최소 7개의 공명하는[36] 행성의 사슬이 발견되었습니다.시뮬레이션에 따르면 행성계 형성 중 행성 배아의 공명 사슬 모양은 원시 가스 디스크의 존재에 의해 선호됩니다.일단 가스가 소멸되면,[37] 관측된 공진 체인의 낮은 주파수와 일치하기 위해 해당 체인의 90-95%가 불안정해져야 합니다.

  • 위에서 언급한 바와 같이, 글리제 876 e, b, c는 4:2:1 비율의 주기(124.3, 61.1, 30.0일)[12][38][39]를 갖는 라플라스 공명에 있습니다.이 경우 L 은(는) 진폭이 40° ± 13°인 라이브러리이며 공진은 시간 평균 [12]관계를 따릅니다.
  • 케플러-223은 공전주기가 8:6:4:3, 공전주기가 3:4:6:8인 공명으로 4개의 행성을 가지고 있습니다(7.3845, 9.8456, 14.7887, 19.7257일).[40][41][42][43]이것은 처음으로 확인된 4체 궤도 [44]공명을 나타냅니다.이 시스템 내의 사서는 다른 행성들이 그들의 궤도의 먼 부분에 있을 때만 두 행성 사이의 밀접한 만남이 발생합니다.시뮬레이션에 따르면 이 공명 시스템은 행성 [43]이동을 통해 형성되었을 것입니다.
  • 케플러-80 d, e, b, c 및 g의 주기는 ~ 1.000: 1.512: 2.296: 3.100: 4.767 비율(3.0722, 4.6449, 7.0525, 9.5236 및 14.6456 일)입니다.그러나, 접속부와 함께 회전하는 기준 프레임에서는, 이것은 4:6:9:12:18의 주기비(9:6:4:3:2의 궤도비)로 감소합니다.관성프레임 또는 비회전프레임(비회전프레임에서 62:41:27:20:13 궤도비 공진에 해당)에서 약 190.5일(회전프레임에서 7개의 완전 주기)마다 반복되는 패턴으로 d와 e, b와 c, c와 g의 결합은 2:3:6:6(9.07, 13.61, 27.21일)의 상대적 간격으로 발생하며,왜냐하면 접속들은 궤도 운동의 반대 방향으로 순환하기 때문입니다.)가능한 3체 공명의 라이브러리는 약 3도의 진폭을 가지고 있으며, 모델링은 공명 시스템이 섭동에 안정적임을 나타냅니다.3중 접속은 [45][35]발생하지 않습니다.
  • TOI-178은 6개의 확인된 행성을 가지고 있으며, 그 중 바깥쪽 5개의 행성은 회전하는 기준 틀에서 비슷한 공명 사슬을 형성하고 있으며, 주기비로 2:4:6:9:12 또는 궤도비로 18:9:6:4:3으로 표현할 수 있습니다.또한 주기가 1.91d인 가장 안쪽의 행성 b는 같은 라플라스 공명 사슬의 일부가 될 수 있는 곳에 가깝게 공전하는데, 이는 행성 c와의 3:5 공명이 ~1.95d 주기로 이루어졌기 때문이며, 이는 행성 b가 그곳에서 진화했을 수도 있지만 아마도 [46]조석력에 의해 공명에서 빠져나왔을 수도 있음을 암시합니다.
  • 트라피스트-1의 대략 지구 크기의 행성 7개는 거의 공명에 가까운(가장 긴 것으로 알려진 사슬) 고리에 있으며, 약 24, 15, 9, 6, 4, 3, 2의 궤도 비율을 갖거나, 약 8/5, 5/3, 3/2, 3/2, 4/3, 3/2(1.603, 1.672, 1.506, 1.509, 1.342, 1.519)의 가장 가까운 주기 비율을 가지고 있습니다.그들은 또한 인접한 행성들의 각 삼중이 라플라스 공명에 있도록 구성되어 있습니다(즉, 한 라플라스 구성에서는 b, c, d, 다른 라플라스 구성에서는 c, d 등).[47][36]공명하는 구성은 행성 이동 [48][49]중에 발생했다고 가정할 때 수십억 년의 시간 척도로 안정적일 것으로 예상됩니다.공명에 대한 음악적 해석이 [49]제공되었습니다.
  • 케플러-29는 7:9 공명을 하는 한 쌍의 [42]행성을 가지고 있습니다. (1/1.28587의 비율)
  • 케플러-36은 6:7 [50]공명에 가까운 한 쌍의 행성을 가지고 있습니다.
  • 케플러-37 d, c, b는 공전 주기가 8:15:24이고 주기가 15:8:5인 공명의 1퍼센트 이내입니다(39.792187, 21.301886,[51] 13.367308일).
  • 케플러-90의 알려진 8개의 행성 중에서, b:c, c:i, i:d의 주기비는 각각 4:5, 3:5, 1:4에 가깝습니다 (4:4.977, 3:4.97, 1:4.13). d, e, f, g, h는 2:3:4:7:11의 주기비에 가깝습니다 (2:3.078:4.182:7.051:11.102; 또한 7:11.021).[52][35] f, g, h는 3:5:8의 주기비에 가깝습니다 (3:5.058:7.964).[53]케플러-36과 같은 시스템과 관련된 계산에 따르면, 외부 거대 가스 행성의 존재는 내부 슈퍼 [54]지구들 사이에 촘촘하게 채워진 공명을 형성하는 것을 용이하게 합니다.
  • HD 41248은 5:7 공명의 0.3% 이내(1/[55]1.39718의 비율)에 한 쌍의 슈퍼지구를 가지고 있습니다.
  • K2-138은 3:2 공명에 가까운 사슬에 5개의 확인된 행성을 가지고 있습니다(주기는 2.353, 3.560, 5.405, 8.261, 12.758일입니다.이 시스템은 시민 과학 프로젝트인 외계행성 탐색기에서 K2 [56]데이터를 사용하여 발견되었습니다.K2-138은 (1:1 평균 운동 [57]공진에서) 공동 궤도체를 수용할 수 있습니다.공진 체인 시스템은 공동 궤도체를[58] 안정화할 수 있으며 HARPS의 K2 광 곡선과 방사 속도에 대한 전용 분석을 통해 [57]이를 밝혀낼 수 있습니다.스피처 우주 망원경의 후속 관측 결과에 따르면 6번째 행성은 3:2 공명 사슬을 이어가며 사슬에 두 개의 틈을 남겼습니다(주기는 41.97일).이러한 틈은 통과하지 않는 더 작은 [59][60]행성들로 채워질 수 있습니다.CHEOPS를 이용한 향후 관측에서는 행성의 질량을 추가로 분석하기 위해 시스템의 통과 타이밍 변동을 측정할 것이며 시스템 [61]내 다른 행성체를 발견할 수도 있습니다.
  • K2-32는 거의 1:2:5:7 공명을 하며 4.34, 8.99, 20.66, 31.71일 주기로 네 개의 행성을 가지고 있습니다.행성의 반지름은 지구와 거의 같습니다.다른 행성들은 해왕성과 [62]토성 사이의 크기를 가지고 있습니다.
  • V1298 Tauri는 c, d, b가 1:2:3 공명(주기 8.25, 12.40, 24.14일)에 가까운 4개의 행성을 확인했습니다.행성 e는 K2 빛 곡선에서 한 번의 통과만을 보여주며 주기는 36일보다 큽니다.행성은 b와 낮은 차수의 공명(2:3, 3:5, 1:2, 1:3)을 하고 있을 것입니다.이 시스템은 매우 어리고(23±4 Myr) 소형 다중 행성 시스템의 전조일지도 모릅니다.2:3 공명은 어떤 가까운 행성들이 공명을 형성하거나 10 Myr 미만의 시간 척도로 진화할 수 있음을 암시합니다.계에 있는 행성들은 해왕성과 토성 사이의 크기를 가지고 있습니다.b행성만이 [63]목성과 비슷한 크기를 가지고 있습니다.
  • HD 158259는 공명 사슬에 가까운 3:2의 주기로 네 개의 행성을 포함하고 있으며(주기는 각각 3.432, 5.198, 7.954, 12.03일, 또는 주기비는 각각 1.51, 1.53, 1.51), 다섯 번째 행성 또한 3:2의 공명에 가까운 것으로 추정됩니다(주기는 17.4일).외계 행성은 반지름 속도법을 [64]사용하여 SOPE 에셸 분광기로 발견되었습니다.
  • 케플러-1649는 9:4 공명에 가까운 두 개의 지구 크기의 행성(주기 19.53527일, 주기 8.689099일, 주기 2.24825)을 포함하고 있으며, 그 중 하나는 생명체 거주가능 영역에 있습니다.13.0일의 주기를 가진 감지되지 않은 행성은 3:[65]2 공명 사슬을 형성할 것입니다.
  • 케플러-88은 1:2 공명(주기비 2.0396)에 가까운 한 쌍의 내행성을 가지고 있으며, 질량비는 ~22.5이며, 가장 안쪽 행성의 통과시기는 ~0.5일로 매우 큽니다.1,[66]400일 궤도에는 훨씬 더 거대한 외계 행성이 있습니다.

1:2 평균 운동 공명에 가까운 외계 행성의 경우는 상당히 흔합니다.통과 방법에 의해 발견된 시스템의 16%는 도플러 분광법으로 특징지어지는 행성계의 6분의 1뿐만 아니라 (1.83–2.[42]18 범위의 주기 비율로)[67] 이것의 예를 가지고 있다고 보고되었습니다.시스템에 대한 불완전한 지식 때문에 실제 비율은 더 [42]높을 것입니다.전체적으로, 방사 속도 특성화된 시스템의 약 3분의 1은 한 쌍의 행성을 동등성에 [42][67]가깝게 가지고 있는 것으로 보입니다.행성 쌍의 궤도 주기 비율이 평균-운동 공명 비율보다 몇 퍼센트 더 작은 것이 훨씬 더 일반적입니다(특히 비율의 정수가 [42]1만큼 다른 1차 공명의 경우).이는 항성과의 조석 상호작용이 [68]중요한 경우에 해당할 것으로 예측되었습니다.

평균 운동의 일치 '근접' 비율

소행성 팔라스의 18:7 목성과의 공명에 가까운 모습을 회전틀로 묘사 (애니메이션은 클릭)목성(왼쪽 위의 분홍색 고리)은 거의 정지해 있습니다.시간이 지남에 따라 목성에 대한 팔라스의 궤도 정렬의 변화는 꾸준히 증가합니다.
지구에 대한 묘사:금성 8시 13분 공명에 근접했습니다.지구가 회전하지 않는 틀의 중심에 정지해 있을 때, 8년 동안의 금성의 연속적인 열등한 결합은 오각형 패턴을 추적합니다(비의 숫자들 사이의 차이를 반영합니다).
명왕성 내부 위성 카론의 주기에 비해 3:4:5:6 정도의 공명을 따르는 작은 네 위성의 궤도도.위성 스틱스, 닉스, 히드라 또한 진정한 3체 공명에 관련되어 있습니다.

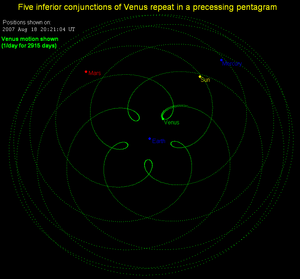
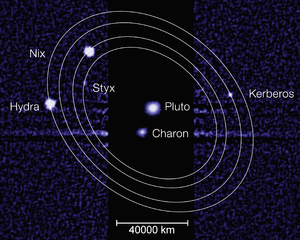
행성이나 주요 위성들의 궤도 진동수 사이의 많은 정수비에 가까운 관계가 때때로 지적됩니다(아래 목록 참조).그러나 이들은 공명을 완벽하게 만들기 위한 적절한 근일점이나 기타 자유도의 세차운동이 없기 때문에 동적인 의미가 없습니다(위의 섹션의 자세한 설명 참조).이러한 근공명은 불일치가 매우 작더라도 동적으로 중요하지 않습니다. 왜냐하면 (실제 공명과 달리) 매 주기 후 물체의 상대적 위치가 이동하기 때문입니다.천문학적으로 짧은 시간에 걸쳐 평균적으로 볼 때, 그들의 상대적인 위치는 공명 근처에 있지 않은 물체들처럼 무작위합니다.예를 들어, 지구 궤도 8번과 금성 궤도 13번을 돌고 나면 거의 같은 모양으로 도착하는 지구와 금성의 궤도를 생각해 보세요.실제 비율은 0.61518624로 정확히 8:13에서 0.032%밖에 차이가 나지 않습니다.8년 후의 불일치는 금성의 궤도운동의 1.5°에 불과합니다.그럼에도 불구하고, 이는 금성과 지구가 960년인 120번의 그러한 주기마다 원래와 반대의 상대적인 방향에 있다는 것을 발견할 수 있는 충분한 양입니다.따라서 수천 년 또는 그 이상의 시간 축척에서는(천문학적 기준으로는 여전히 작음) 상대적 위치가 사실상 무작위적입니다.

근공명이 존재하는 것은 과거에 완벽한 공명이 존재했거나 미래에 그 계가 하나를 향해 진화하고 있다는 것을 반영할 수 있습니다.

궤도 주기의 일치는 다음과 같습니다.

어떤 궤도 주파수 일치가
(비율) 및 본체 한 주기[a] 후 불일치 랜덤화시간[b] 확률[c]
플래닛
(9:23) 금성-수은 4.0° 200 y 0.19
(8:13) 지구-비너스[69][70][d] 1.5° 1000 y 0.065
(243:395) 지구-비너스[69][71] 0.8° 5만 y 0.68
(1:3) 화성-비너스 20.6° 이십이 0.11
(1:2) 화성-지구 42.9° 8 y 0.24
(1:12) 목성-지구[e] 49.1° 40 y 0.28
(2:5) 토성-목성[f] 12.8° 800 y 0.13
(1:7) 천왕성 목성 31.1° 오백년 0.18
(7:20) 천왕성-토성 5.7° 2만 y 0.20
(5:28) 해왕성 – 토성 1.9° 80,000 y 0.052
(1:2) 해왕성-우라누스 14.0° 2000 y 0.078
화성계
(1:4) 데이모스-포보스[g] 14.9° 0.04 y 0.083
주요 소행성
(1:1) 팔라스-세레스[73][74] 0.7° 1000 y 0.0039[h]
(7:18) 목성-팔라스[75] 0.10° 십만 y 0.0040[i]
87 실비아 계[j]
(17:45) 로물루스-레무스 0.7° 40 y 0.067
목성계
(1:6) 이오-메티스 0.6° 2 y 0.0031
(3:5) 아말테아아드라스테아 3.9° 0.2 y 0.064
(3:7) 칼리스토-가니메데[76] 0.7° 30 y 0.012
토성계
(2:3) 엔켈라두스-미마스 33.2° 0.04 y 0.33
(2:3) 디오네-타이스[k] 36.2° 0.07 y 0.36
(3:5) 레아-디오네 17.1° 0.4 y 0.26
(2:7) 타이탄 레아 21.0° 0.7 y 0.22
(1:5) 이아페토스-티탄 9.2° 4 y 0.051
큰센타우르스[l]
(3:4) 천왕성-차릴로 4.5° 10,000 0.073
천왕성계
(3:5) 로잘린드-코델리아[78] 0.22° 4 y 0.0037
(1:3) 움브리엘-미란다[m] 24.5° 0.08 y 0.14
(3:5) 엄브리엘-아리엘[n] 24.2° 0.3 y 0.35
(1:2) 티타니아-엄브리엘 36.3° 0.1 y 0.20
(2:3) 오베론-티타니아 33.4° 0.4 y 0.34
해왕성계
(1:20) 트리톤-나이아드 13.5° 0.2 y 0.075
(1:2) 프로테우스–라리사[81][82] 8.4° 0.07 y 0.047
(5:6) 프로테우스-해마 2.1° 1 y 0.057
명왕성계
(1:3) Styx-Charon[83] 58.5° 0.2 y 0.33
(1:4) 닉스-카론[83][84] 39.1° 0.3 y 0.22
(1:5) 케르베로스-카론[83] 9.2° 2 y 0.05
(1:6) 히드라-카론[83][84] 6.6° 3 y 0.037
하우메아계
(3:8) 히시아카-나마카[o] 42.5° 2 y 0.55
  1. ^ 주기 시작 시의 위치와 비교하여 내부 물체의 궤도 경도가 일치하지 않습니다(주기는 외부 물체의 n개 궤도로 정의됨 – 아래 참조).원형 궤도가 가정됩니다(즉, 세차운동이 무시됨).
  2. ^ 물체의 초기 상대적인 세로 방향 궤도 위치에서 일치하지 않는 부분이 가장 가까운 첫 번째 유효숫자로 반올림한 180°로 증가하는 데 필요한 시간.
  3. ^ n번의 시도에서 적어도 한 번은 같은 궤도 일치를 얻거나 더 작은 궤도 일치를 얻을 확률. 여기서 n은 주기당 외부 물체의 궤도의 정수이며, 일치하지 않는 궤도는 임의로 0°에서 180° 사이에서 달라진다고 가정합니다.이 값은 1-(1- 불일치/n180°)로 계산됩니다.이것은 상대적인 확률에 대한 대략적인 생각만을 시도하는 대략적인 계산입니다.
  4. ^ 지구와 금성에 나열된 두 개의 근접한 지수는 243년마다 반복되는 주기로 8년 [69][71]간격으로 발생하는 금성의 통과 시기에 반영됩니다.
  5. ^ 목성과 지구 사이의 1:12 공명에 가까운 것은 목성과의 3:1 공명을 차지하고 있거나 가까이 있는 알린다 소행성이 지구와의 1:4 공명에 가까운 것을 야기합니다.
  6. ^ 이 공명에 가까운 것을 대불평등이라고 부릅니다.라플라스는 1784년에서 1789년 사이에 출판된 일련의 논문에서 처음 기술했습니다.
  7. ^ 지금은 사라진 내달과의 공명이 포보스와 데이모스의 [72]형성에 관여했을 것으로 보입니다.
  8. ^ 적절한 공전 주기를 기준으로 팔라스와 세레스의 경우 각각 1684.869일과 1681.601일.
  9. ^ 팔라스의 고유 공전 주기를 기준으로 할 때, 1684.869일, 목성의 경우 4332.59일입니다.
  10. ^ 87 Sylvia는 달을 하나 이상 가지고 있는 것으로 발견된 최초의 소행성입니다.
  11. ^ 이 공명은 [77]과거에 사용되었을 수도 있습니다.
  12. ^ 센타우루스의 일부 정의는 그들이 비공진체라고 규정합니다.
  13. ^ 이 공명은 [79]과거에 사용되었을 수도 있습니다.
  14. ^ 이 공명은 [80]과거에 사용되었을 수도 있습니다.
  15. ^ Haumea 계에 대한 결과는 큰 의미가 없습니다. 왜냐하면 계산에서 암시된 가정과 달리 Namaka는 빠르게 진행하는 편심한 비케플러 궤도를 가지고 있기 때문입니다(아래 참조).히시아카와 나마카는 표시된 것보다 3:8 공명에 훨씬 더 가까우며 실제로 그 [85]안에 있을지도 모릅니다.

이 목록에서 가장 가능성이 낮은 궤도 상관 관계는 이오와 메티스 사이, 그 다음으로는 로잘린드와 코델리아, 팔라스와 세레스, 목성과 팔라스, 칼리스토와 가니메데, 히드라와 카론 사이의 상관 관계입니다.

가능한 과거 평균 운동 공진

목성과 토성 사이의 과거 공명은 초기 태양계 역사에서 극적인 역할을 했을지도 모릅니다.니스에 있는 코트다쥐르 천문대의 알레산드로 모르비델리의 2004년 컴퓨터 모델은 목성과 토성 사이에 1:2 공명이 형성되는 것을 제안했습니다.이 모델에서, 이것은 천왕성과 해왕성을 더 높은 궤도로 밀어내는 중력을 만들어냈고, 어떤 시나리오에서는 그것들이 위치를 바꾸게 했고, 이것은 해왕성과 태양 사이의 거리를 두 배로 늘렸을 것입니다.해왕성이 바깥쪽으로 이동함에 따라 카이퍼 원형대에서 물체가 떨어져 나간 결과, 태양계가 형성된 지 6억 년이 지난 뒤에 일어난 후기 대폭격과 목성의 [86]트로이 소행성의 기원을 설명할 수 있을 것입니다.해왕성의 바깥쪽으로의 이동은 카이퍼대 내의 일부 공명(특히 2:5 공명)의 현재 점유를 설명할 수 있습니다.

토성의 중간 크기 위성인 디오네와 테티스는 현재 정확한 공명에 근접하지는 않았지만, 그들은 태양계 역사 초기에 2:3 공명을 하고 있었을지도 모릅니다.이것은 궤도 이심률과 조석 가열로 이어졌을 것이며, 테티스의 내부는 지하 바다를 형성할 수 있을 정도로 충분히 따뜻했을 것입니다.위성들이 공명으로부터 빠져나간 후 바다가 계속해서 얼어붙으면서 [77]테티스에 있는 이타카 차스마의 거대한 그라벤 시스템을 만든 광범위한 응력이 발생했을 수도 있습니다.

천왕성의 위성계는 큰 위성들 사이에 정확한 공명이 없다는 점에서 목성과 토성의 위성계와 눈에 띄게 다르며, 목성(4개 중 3개)과 토성(8개 중 6개)의 큰 위성들은 평균운동 공명에 있습니다.세 위성 시스템 모두에서 위성이 1차 회전 에너지를 희생시켜 궤도 에너지를 얻는 과정인 조석 소멸로 인해 궤도가 이동하면서 위성은 평균 운동 공명에 포착되어 내부 위성에 불균형적으로 영향을 미쳤을 가능성이 있습니다.그러나, 행성의 편평도가 낮고 위성의 상대적인 크기가 크기 때문에, 평균 운동 공명으로부터 탈출하는 것은 훨씬 쉽습니다.일차의 편평도가 낮으면 중력장이 서로 다른 가능한 공명들이 서로 더 가깝게 배치되는 방식으로 바뀝니다.상대적인 위성 크기가 클수록 상호작용의 강도가 높아집니다.두 요인 모두 평균 운동 공명에서 또는 그 근처에서 더 혼란스러운 궤도 거동을 초래합니다.공명으로부터의 탈출은 2차 공명으로의 포획 및/또는 조석 진화에 의한 궤도 이심률 또는 기울기의 증가와 관련될 수 있습니다.

천왕성계에 한때 존재했을 것으로 추정되는 평균운동 공명에는 (3:5) 아리엘-미란다, (1:3) 움브리엘-미란다, (3:5) 움브리엘-아리엘,[80][79] 그리고 (1:4) 티타니아-아리엘이 있습니다.이러한 과거 공명에 대한 증거로는 천왕성 내부 위성의 궤도 이심률이 상대적으로 높고 미란다의 궤도 경사가 비정상적으로 높다는 것이 있습니다.(1:3) 움브리엘-미란다와 (1:4) 티타니아-아리엘 공명과 관련된 높은 과거 궤도 이심률은 각각 미란다와 아리엘 [87]내부의 조석 가열로 이어졌을 수 있습니다.미란다는 2차 공명을 통해 움브리엘과의 공명에서 탈출했을 가능성이 있으며, 이 탈출의 메커니즘은 왜 궤도 경사가 다른 일반적인 우라니아 위성들의 10배 이상인지를 설명하는 것으로 생각됩니다(천왕성의 자연 위성 [88][89]참조).

미란다의 경우와 마찬가지로 목성의 위성 아말테아와 테베의 현재 성향은 각각 [90]이오와의 3:1 공명과 4:2 공명을 통과한 과거의 징후로 생각됩니다.

해왕성의 일반 위성 프로테우스와 라리사는 몇 억 년 전에 1:2 공명을 통해 통과한 것으로 생각됩니다. 프로테우스가 동기 궤도 밖에 있고 라리사가 1 안에 있기 때문에 그 이후로 그 위성들은 서로 멀어졌습니다.공명을 통과하는 것은 두 위성의 이심률을 그 이후 완전히 [81][82]감쇠되지 않은 정도로 흥분시킨 것으로 생각됩니다.

명왕성의 위성들의 경우, 현재의 근공명은 카론 궤도의 이심률의 조석 감쇠로 인해 교란된 이전의 정확한 공명의 흔적이라고 제안되었습니다(자세한 내용은 명왕성의 자연 위성을 참조하십시오).가까운 공명은 명왕성-카론 중력장에서 15%의 국소적인 요동에 의해 유지될 수 있습니다.따라서 이러한 가까운 공명은 우연이 아닐 수도 있습니다.

왜행성 하우메아의 작은 내달인 나마카는 큰 외달인 히시아카의 질량의 10분의 1입니다.나마카는 케플러가 아닌 편심 궤도를 따라 18일 안에 하우메아 주위를 공전하며,[85] 2008년 기준으로 히시아카로부터 13° 기울어져 있습니다.시스템의 시간이 지남에 따라, 그것은 조수적으로 더 원형의 궤도로 감쇠되었어야 합니다.조석 소멸로 인해 하우메아에서 바깥쪽으로 이동하면서 궤도가 수렴하면서 더 거대한 히시아카와의 공명에 의해 방해를 받은 것으로 보입니다.그 위성들은 궤도 공명에 여러 번 걸렸다가 탈출했을 수도 있습니다.그들은 아마도 비교적 최근에 3:1 공명을 통과했을 것이고, 현재는 8:3 공명에 있거나 최소한 가까이 있을 것입니다.나마카의 궤도는 매우 교란되어 있으며,[85] 1년에 -6.5°의 세차운동이 진행되고 있습니다.

참고 항목

메모들

  1. ^ 이 공명의 성질은 대략 다음과 같이 궤도 주기에서 구할 수 있습니다.Showalter et al.,[34] 2019로부터 Naiad(Pn)와 Thalassa(Pt)의 기간은 각각 0.294396일과 0.311484일입니다.이로부터 합 사이의 주기는 5.366일(1/[1/Pn – 1/Pt])로 계산할 수 있으며, 이는 나이아드 18.23(최소 18.25) 궤도, 탈라사 17.23(최소 17.25) 궤도입니다.따라서 네 번의 접속 기간을 거쳐 나이아드 73회, 탈라사 69회 궤도가 지나 원래의 형상으로 복원됩니다.

참고문헌

  1. ^ "IAU 2006 General Assembly: Resolutions 5 and 6" (PDF). IAU. 24 August 2006. Retrieved 23 June 2009.
  2. ^ a b Porco, C.; Nicholson, P. D.; Borderies, N.; Danielson, G. E.; Goldreich, P.; Holdberg, J. B.; Lane, A. L. (1984). "The eccentric Saturnian ringlets at 1.29Rs and 1.45Rs". Icarus. 60 (1): 1–16. Bibcode:1984Icar...60....1P. doi:10.1016/0019-1035(84)90134-9.
  3. ^ Rosen, P. A.; Lissauer, J. J. (1988). "The Titan −1:0 Nodal Bending Wave in Saturn's Ring C". Science. 241 (4866): 690–694. Bibcode:1988Sci...241..690R. doi:10.1126/science.241.4866.690. PMID 17839081. S2CID 32938282.
  4. ^ Chakrabarti, S. K.; Bhattacharyya, A. (2001). "Constraints on the C ring parameters of Saturn at the Titan -1:0 resonance". Monthly Notices of the Royal Astronomical Society. 326 (2): L23. Bibcode:2001MNRAS.326L..23C. doi:10.1046/j.1365-8711.2001.04813.x.
  5. ^ Witze, A. (5 September 2018). "The quest to conquer Earth's space junk problem". Nature. 561 (7721): 24–26. Bibcode:2018Natur.561...24W. doi:10.1038/d41586-018-06170-1. PMID 30185967.
  6. ^ Daquin, J.; Rosengren, A. J.; Alessi, E. M.; Deleflie, F.; Valsecchi, G. B.; Rossi, A. (2016). "The dynamical structure of the MEO region: long-term stability, chaos, and transport". Celestial Mechanics and Dynamical Astronomy. 124 (4): 335–366. arXiv:1507.06170. Bibcode:2016CeMDA.124..335D. doi:10.1007/s10569-015-9665-9. S2CID 119183742.
  7. ^ Wiegert, P.; Connors, M.; Veillet, C. (30 March 2017). "A retrograde co-orbital asteroid of Jupiter". Nature. 543 (7647): 687–689. Bibcode:2017Natur.543..687W. doi:10.1038/nature22029. PMID 28358083. S2CID 205255113.
  8. ^ a b Morais, M. H. M.; Namouni, F. (21 September 2013). "Asteroids in retrograde resonance with Jupiter and Saturn". Monthly Notices of the Royal Astronomical Society Letters. 436: L30–L34. arXiv:1308.0216. Bibcode:2013MNRAS.436L..30M. doi:10.1093/mnrasl/slt106. S2CID 119263066.
  9. ^ Morais, Maria Helena Moreira; Namouni, Fathi (12 October 2013). "Retrograde resonance in the planar three-body problem". Celestial Mechanics and Dynamical Astronomy. 117 (4): 405–421. arXiv:1305.0016. Bibcode:2013CeMDA.117..405M. doi:10.1007/s10569-013-9519-2. ISSN 1572-9478. S2CID 254379849.
  10. ^ Morais, M. H. M.; Nomouni, F. (2017). "First transneptunian object in polar resonance with Neptune". Letters. Monthly Notices of the Royal Astronomical Society. 472 (1): L1–L4. arXiv:1708.00346. Bibcode:2017MNRAS.472L...1M. doi:10.1093/mnrasl/slx125.
  11. ^ Barnes, R. (2011). "Laplace Resonance". In Gargaud, M. (ed.). Encyclopedia of Astrobiology. Springer Science+Business Media. pp. 905–906. doi:10.1007/978-3-642-11274-4_864. ISBN 978-3-642-11271-3.
  12. ^ a b c Rivera, E. J.; Laughlin, G.; Butler, R. P.; Vogt, S. S.; Haghighipour, N.; Meschiari, S. (2010). "The Lick-Carnegie Exoplanet Survey: A Uranus-mass Fourth Planet for GJ 876 in an Extrasolar Laplace Configuration". The Astrophysical Journal. 719 (1): 890–899. arXiv:1006.4244. Bibcode:2010ApJ...719..890R. doi:10.1088/0004-637X/719/1/890. S2CID 118707953.
  13. ^ Nelson, B. E.; Robertson, P. M.; Payne, M. J.; Pritchard, S. M.; Deck, K. M.; Ford, E. B.; Wright, J. T.; Isaacson, H. T. (2015). "An empirically derived three-dimensional Laplace resonance in the Gliese 876 planetary system". Monthly Notices of the Royal Astronomical Society. 455 (3): 2484–2499. doi:10.1093/mnras/stv2367.
  14. ^ Marti, J. G.; Giuppone, C. A.; Beauge, C. (2013). "Dynamical analysis of the Gliese-876 Laplace resonance". Monthly Notices of the Royal Astronomical Society. 433 (2): 928–934. arXiv:1305.6768. Bibcode:2013MNRAS.433..928M. doi:10.1093/mnras/stt765. S2CID 118643833.
  15. ^ a b c d Showalter, M. R.; Hamilton, D. P. (2015). "Resonant interactions and chaotic rotation of Pluto's small moons". Nature. 522 (7554): 45–49. Bibcode:2015Natur.522...45S. doi:10.1038/nature14469. PMID 26040889. S2CID 205243819.
  16. ^ Murray, C. D.; Dermott, S. F. (1999). Solar System Dynamics. Cambridge University Press. p. 17. ISBN 978-0-521-57597-3.
  17. ^ Beatty, J. K. (23 July 2003). "Why Is Saturn Tipsy?". Sky & Telescope. Archived from the original on 3 September 2009. Retrieved 25 February 2009.
  18. ^ Ward, W. R.; Hamilton, D. P. (2004). "Tilting Saturn. I. Analytic Model". The Astronomical Journal. 128 (5): 2501–2509. Bibcode:2004AJ....128.2501W. doi:10.1086/424533.
  19. ^ Hamilton, D. P.; Ward, W. R. (2004). "Tilting Saturn. II. Numerical Model". The Astronomical Journal. 128 (5): 2510–2517. Bibcode:2004AJ....128.2510H. doi:10.1086/424534. S2CID 33083447.
  20. ^ Maryame El Moutamid (15 September 2022). "How Saturn got its tilt and its rings". Science. 377 (6612): 1264–1265. Bibcode:2022Sci...377.1264E. doi:10.1126/science.abq3184. PMID 36108002. S2CID 252309068.
  21. ^ Jack Wisdom; et al. (15 September 2022). "Loss of a satellite could explain Saturn's obliquity and young rings". Science. 377 (6612): 1285–1289. Bibcode:2022Sci...377.1285W. doi:10.1126/science.abn1234. PMID 36107998. S2CID 252310492.
  22. ^ Laskar, J. (2008). "Chaotic diffusion in the Solar System". Icarus. 196 (1): 1–15. arXiv:0802.3371. Bibcode:2008Icar..196....1L. doi:10.1016/j.icarus.2008.02.017. S2CID 11586168.
  23. ^ Laskar, J.; Gastineau, M. (2009). "Existence of collisional trajectories of Mercury, Mars and Venus with the Earth". Nature. 459 (7248): 817–819. Bibcode:2009Natur.459..817L. doi:10.1038/nature08096. PMID 19516336. S2CID 4416436.
  24. ^ Musotto, S.; Varad, F.; Moore, W.; Schubert, G. (2002). "Numerical Simulations of the Orbits of the Galilean Satellites". Icarus. 159 (2): 500–504. Bibcode:2002Icar..159..500M. doi:10.1006/icar.2002.6939.
  25. ^ Brown, M. E.; Barkume, K. M.; Ragozzine, D.; Schaller, E. L. (2007). "A collisional family of icy objects in the Kuiper belt" (PDF). Nature. 446 (7133): 294–296. Bibcode:2007Natur.446..294B. doi:10.1038/nature05619. PMID 17361177. S2CID 4430027.
  26. ^ Ragozzine, D.; Brown, M. E. (2007). "Candidate members and age estimate of the family of Kuiper Belt object 2003 EL61". The Astronomical Journal. 134 (6): 2160–2167. arXiv:0709.0328. Bibcode:2007AJ....134.2160R. doi:10.1086/522334. S2CID 8387493.
  27. ^ Buie, M. W. (24 October 2011). "Orbit Fit and Astrometric record for 225088". SwRI (Space Science Department). Retrieved 14 November 2014.
  28. ^ Sinclair, A. T. (1975). "The Orbital Resonance Amongst the Galilean Satellites of Jupiter". Monthly Notices of the Royal Astronomical Society. 171 (1): 59–72. Bibcode:1975MNRAS.171...59S. doi:10.1093/mnras/171.1.59.
  29. ^ Witze, A. (3 June 2015). "Pluto's moons move in synchrony". Nature News. doi:10.1038/nature.2015.17681. S2CID 134519717.
  30. ^ Malhotra, R. (1997). "Pluto's Orbit". Retrieved 26 March 2007.
  31. ^ Brown, M. E. (23 March 2009). "S/2005 (90482) 1 needs your help". Mike Brown's Planets. Retrieved 25 March 2009.
  32. ^ "NASA Finds Neptune Moons Locked in 'Dance of Avoidance'". Jet Propulsion Laboratory. 14 November 2019. Retrieved 15 November 2019.
  33. ^ Brozović, M.; Showalter, M. R.; Jacobson, R. A.; French, R. S.; Lissauer, J. J.; de Pater, I. (31 October 2019). "Orbits and resonances of the regular moons of Neptune". Icarus. 338 (2): 113462. arXiv:1910.13612. doi:10.1016/j.icarus.2019.113462. S2CID 204960799.
  34. ^ Showalter, M. R.; de Pater, I.; Lissauer, J. J.; French, R. S.url= https://www.spacetelescope.org/static/archives/releases/science_papers/heic1904/heic1904a.pdf (2019). "The seventh inner moon of Neptune". Nature. 566 (7744): 350–353. Bibcode:2019Natur.566..350S. doi:10.1038/s41586-019-0909-9. PMC 6424524. PMID 30787452. {{cite journal}}:에외부 링크 first4=(도움말)
  35. ^ a b c Shale, C. J.; Vanderburg, A. (2017). "Identifying Exoplanets With Deep Learning: A Five Planet Resonant Chain Around Kepler-80 And An Eighth Planet Around Kepler-90" (PDF). The Astrophysical Journal. 155 (2): 94. arXiv:1712.05044. Bibcode:2018AJ....155...94S. doi:10.3847/1538-3881/aa9e09. S2CID 4535051. Retrieved 15 December 2017.
  36. ^ a b Luger, R.; Sestovic, M.; Kruse, E.; Grimm, S. L.; Demory, B.-O.; Agol, E.; Bolmont, E.; Fabrycky, D.; Fernandes, C. S.; Van Grootel, V.; Burgasser, A.; Gillon, M.; Ingalls, J. G.; Jehin, E.; Raymond, S. N.; Selsis, F.; Triaud, A. H. M. J.; Barclay, T.; Barentsen, G.; Delrez, L.; de Wit, J.; Foreman-Mackey, D.; Holdsworth, D. L.; Leconte, J.; Lederer, S.; Turbet, M.; Almleaky, Y.; Benkhaldoun, Z.; Magain, P.; Morris, B. (22 May 2017). "A seven-planet resonant chain in TRAPPIST-1". Nature Astronomy. 1 (6): 0129. arXiv:1703.04166. Bibcode:2017NatAs...1E.129L. doi:10.1038/s41550-017-0129. S2CID 54770728.
  37. ^ Izidoro, A.; Ogihara, M.; Raymond, S. N.; Morbidelli, A.; Pierens, A.; Bitsch, B.; Cossou, C.; Hersant, F. (2017). "Breaking the chains: hot super-Earth systems from migration and disruption of compact resonant chains". Monthly Notices of the Royal Astronomical Society. 470 (2): 1750–1770. arXiv:1703.03634. Bibcode:2017MNRAS.470.1750I. doi:10.1093/mnras/stx1232. S2CID 119493483.
  38. ^ Laughlin, G. (23 June 2010). "A second Laplace resonance". Systemic: Characterizing Planets. Archived from the original on 29 December 2013. Retrieved 30 June 2015.
  39. ^ Marcy, Ge. W.; Butler, R. P.; Fischer, D.; Vogt, S. S.; Lissauer, J. J.; Rivera, E. J. (2001). "A Pair of Resonant Planets Orbiting GJ 876". The Astrophysical Journal. 556 (1): 296–301. Bibcode:2001ApJ...556..296M. doi:10.1086/321552.
  40. ^ "Planet Kepler-223 b". Extrasolar Planets Encyclopaedia. Archived from the original on 22 January 2018. Retrieved 21 January 2018.
  41. ^ Beatty, K. (5 March 2011). "Kepler Finds Planets in Tight Dance". Sky and Telescope. Retrieved 16 October 2012.
  42. ^ a b c d e f Lissauer, J. J.; et al. (2011). "Architecture and dynamics of Kepler's candidate multiple transiting planet systems". The Astrophysical Journal Supplement Series. 197 (1): 1–26. arXiv:1102.0543. Bibcode:2011ApJS..197....8L. doi:10.1088/0067-0049/197/1/8. S2CID 43095783.
  43. ^ a b Mills, S. M.; Fabrycky, D. C.; Migaszewski, C.; Ford, E. B.; Petigura, E.; Isaacson, H. (11 May 2016). "A resonant chain of four transiting, sub-Neptune planets". Nature. 533 (7604): 509–512. arXiv:1612.07376. Bibcode:2016Natur.533..509M. doi:10.1038/nature17445. PMID 27225123. S2CID 205248546.
  44. ^ Koppes, S. (17 May 2016). "Kepler-223 System: Clues to Planetary Migration". Jet Propulsion Lab. Retrieved 18 May 2016.
  45. ^ MacDonald, M. G.; Ragozzine, D.; Fabrycky, D. C.; Ford, E. B.; Holman, M. J.; Isaacson, H. T.; Lissauer, J. J.; Lopez, E. D.; Mazeh, T. (1 January 2016). "A Dynamical Analysis of the Kepler-80 System of Five Transiting Planets". The Astronomical Journal. 152 (4): 105. arXiv:1607.07540. Bibcode:2016AJ....152..105M. doi:10.3847/0004-6256/152/4/105. S2CID 119265122.
  46. ^ Leleu, A.; Alibert, Y.; Hara, N. C.; Hooton, M. J.; Wilson, T. G.; Robutel, P.; Delisle, J. -B.; Laskar, J.; Hoyer, S.; Lovis, C.; Bryant, E. M.; Ducrot, E.; Cabrera, J.; Delrez, L.; Acton, J. S.; Adibekyan, V.; Allart, R.; Prieto, Allende; Alonso, R.; Alves, D.; et al. (20 January 2021). "Six transiting planets and a chain of Laplace resonances in TOI-178". Astronomy & Astrophysics. 649: A26. arXiv:2101.09260. Bibcode:2021A&A...649A..26L. doi:10.1051/0004-6361/202039767. ISSN 0004-6361. S2CID 231693292.
  47. ^ Gillon, M.; Triaud, A. H. M. J.; Demory, B.-O.; Jehin, E.; Agol, E.; Deck, K. M.; Lederer, S. M.; de Wit, J.; Burdanov, A. (22 February 2017). "Seven temperate terrestrial planets around the nearby ultracool dwarf star TRAPPIST-1". Nature. 542 (7642): 456–460. arXiv:1703.01424. Bibcode:2017Natur.542..456G. doi:10.1038/nature21360. PMC 5330437. PMID 28230125.
  48. ^ Tamayo, D.; Rein, H.; Petrovich, C.; Murray, N. (10 May 2017). "Convergent Migration Renders TRAPPIST-1 Long-lived". The Astrophysical Journal. 840 (2): L19. arXiv:1704.02957. Bibcode:2017ApJ...840L..19T. doi:10.3847/2041-8213/aa70ea. S2CID 119336960.
  49. ^ a b Chang, K. (10 May 2017). "The Harmony That Keeps Trappist-1's 7 Earth-size Worlds From Colliding". The New York Times. Retrieved 26 June 2017.
  50. ^ Carter, J. A.; Agol, E.; Chaplin, W. J.; et al. (21 June 2012). "Kepler-36: A Pair of Planets with Neighboring Orbits and Dissimilar Densities". Science. 337 (6094): 556–559. arXiv:1206.4718. Bibcode:2012Sci...337..556C. doi:10.1126/science.1223269. PMID 22722249. S2CID 40245894.
  51. ^ Barclay, T.; et al. (2013). "A sub-Mercury-sized exoplanet". Nature. 494 (7438): 452–454. arXiv:1305.5587. Bibcode:2013Natur.494..452B. doi:10.1038/nature11914. PMID 23426260. S2CID 205232792.
    • 그리고
  52. ^ Lissauer, J. J.; Marcy, G. W.; Bryson, S. T.; Rowe, J. F.; Jontof-Hutter, D.; Agol, E.; Borucki, W. J.; Carter, J. A.; Ford, E. B.; Gilliland, R. L.; Kolbl, R.; Star, K. M.; Steffen, J. H.; Torres, G. (25 February 2014). "Validation of Kepler's Multiple Planet Candidates. II: Refined Statistical Framework and Descriptions of Systems of Special Interest". The Astrophysical Journal. 784 (1): 44. arXiv:1402.6352. Bibcode:2014ApJ...784...44L. doi:10.1088/0004-637X/784/1/44. S2CID 119108651.
  53. ^ Cabrera, J.; Csizmadia, Sz.; Lehmann, H.; Dvorak, R.; Gandolfi, D.; Rauer, H.; Erikson, A.; Dreyer, C.; Eigmüller, Ph.; Hatzes, A. (31 December 2013). "The Planetary System to KIC 11442793: A Compact Analogue to the Solar System". The Astrophysical Journal. 781 (1): 18. arXiv:1310.6248. Bibcode:2014ApJ...781...18C. doi:10.1088/0004-637X/781/1/18. S2CID 118875825.
  54. ^ Hands, T. O.; Alexander, R. D. (13 January 2016). "There might be giants: unseen Jupiter-mass planets as sculptors of tightly packed planetary systems". Monthly Notices of the Royal Astronomical Society. 456 (4): 4121–4127. arXiv:1512.02649. Bibcode:2016MNRAS.456.4121H. doi:10.1093/mnras/stv2897. S2CID 55175754.
  55. ^ Jenkins, J. S.; Tuomi, M.; Brasser, R.; Ivanyuk, O.; Murgas, F. (2013). "Two Super-Earths Orbiting the Solar Analog HD 41248 on the Edge of a 7:5 Mean Motion Resonance". The Astrophysical Journal. 771 (1): 41. arXiv:1304.7374. Bibcode:2013ApJ...771...41J. doi:10.1088/0004-637X/771/1/41. S2CID 14827197.
  56. ^ Christiansen, Jessie L.; Crossfield, Ian J. M.; Barentsen, G.; Lintott, C. J.; Barclay, T.; Simmons, B. D.; Petigura, E.; Schlieder, J. E.; Dressing, C. D.; Vanderburg, A.; Allen, C. (11 January 2018). "The K2-138 System: A Near-resonant Chain of Five Sub-Neptune Planets Discovered by Citizen Scientists". The Astronomical Journal. 155 (2): 57. arXiv:1801.03874. Bibcode:2018AJ....155...57C. doi:10.3847/1538-3881/aa9be0. S2CID 52971376.
  57. ^ a b Lopez, T. A.; Barros, S. C. C.; Santerne, A.; Deleuil, M.; Adibekyan, V.; Almenara, J.-M.; Armstrong, D. J.; Brugger, B.; Barrado, D.; Bayliss, D.; Boisse, I.; Bonomo, A. S.; Bouchy, F.; Brown, D. J. A.; Carli, E.; Demangeon, O.; Dumusque, X.; Díaz, R. F.; Faria, J. P.; Figueira, P.; Foxell, E.; Giles, H.; Hébrard, G.; Hojjatpanah, S.; Kirk, J.; Lillo-Box, J.; Lovis, C.; Mousis, O.; da Nóbrega, H. J.; Nielsen, L. D.; Neal, J. J.; Osborn, H. P.; Pepe, F.; Pollacco, D.; Santos, N. C.; Sousa, S. G.; Udry, S.; Vigan, A.; Wheatley, P. J. (1 November 2019). "Exoplanet characterisation in the longest known resonant chain: the K2-138 system seen by HARPS". Astronomy & Astrophysics. 631: A90. arXiv:1909.13527. Bibcode:2019A&A...631A..90L. doi:10.1051/0004-6361/201936267. S2CID 203593804.
  58. ^ Leleu, Adrien; Coleman, Gavin A. L.; Ataiee, S. (1 November 2019). "Stability of the co-orbital resonance under dissipation – Application to its evolution in protoplanetary discs". Astronomy & Astrophysics. 631: A6. arXiv:1901.07640. Bibcode:2019A&A...631A...6L. doi:10.1051/0004-6361/201834486. S2CID 219840769.
  59. ^ "K2-138 System Diagram". www.jpl.nasa.gov. Retrieved 20 November 2019.
  60. ^ Hardegree-Ullman, K.; Christiansen, J. (January 2019). "K2-138 g: Spitzer Spots a Sixth Sub-Neptune for the Citizen Science System". American Astronomical Society Meeting Abstracts #233. 233: 164.07. Bibcode:2019AAS...23316407H.
  61. ^ "AO-1 Programmes – CHEOPS Guest Observers Programme – Cosmos". www.cosmos.esa.int. Retrieved 20 November 2019.
  62. ^ Heller, René; Rodenbeck, Kai; Hippke, Michael (1 May 2019). "Transit least-squares survey – I. Discovery and validation of an Earth-sized planet in the four-planet system K2-32 near the 1:2:5:7 resonance". Astronomy & Astrophysics. 625: A31. arXiv:1904.00651. Bibcode:2019A&A...625A..31H. doi:10.1051/0004-6361/201935276. ISSN 0004-6361. S2CID 90259349.
  63. ^ David, Trevor J.; Petigura, Erik A.; Luger, Rodrigo; Foreman-Mackey, Daniel; Livingston, John H.; Mamajek, Eric E.; Hillenbrand, Lynne A. (29 October 2019). "Four Newborn Planets Transiting the Young Solar Analog V1298 Tau". The Astrophysical Journal. 885 (1): L12. arXiv:1910.04563. Bibcode:2019ApJ...885L..12D. doi:10.3847/2041-8213/ab4c99. ISSN 2041-8213. S2CID 204008446.
  64. ^ Hara, N. C.; Bouchy, F.; Stalport, M.; Boisse, I.; Rodrigues, J.; Delisle, J.- B.; Santerne, A.; Henry, G. W.; Arnold, L.; Astudillo-Defru, N.; Borgniet, S. (2020). "The SOPHIE search for northern extrasolar planets. XVII. A compact planetary system in a near 3:2 mean motion resonance chain". Astronomy & Astrophysics. 636: L6. arXiv:1911.13296. doi:10.1051/0004-6361/201937254. S2CID 208512859.
  65. ^ Vanderburg, A.; Rowden, P.; Bryson, S.; Coughlin, J.; Batalha, N.; Collins, K.A.; Latham, D.W.; Mullally, S.E.; Colón, K.D.; Henze, C.; Huang, C.X.; Quinn, S.N. (2020). "A Habitable-zone Earth-sized Planet Rescued from False Positive Status". The Astrophysical Journal. 893 (1): L27. arXiv:2004.06725. Bibcode:2020ApJ...893L..27V. doi:10.3847/2041-8213/ab84e5. S2CID 215768850.
  66. ^ Weiss, L.M.; Fabrycky, D.C.; Agol, E.; Mills, S.M.; Howard, A.W.; Isaacson, H.; Petigura, E.A.; Fulton, B.; Hirsch, L.; Sinukoff, E. (2020). "The Discovery of the Long-Period, Eccentric Planet Kepler-88 d and System Characterization with Radial Velocities and Photodynamical Analysis" (PDF). The Astronomical Journal. 159 (5): 242. arXiv:1909.02427. Bibcode:2020AJ....159..242W. doi:10.3847/1538-3881/ab88ca. S2CID 202539420.
  67. ^ a b Wright, J. T.; Fakhouri, O.; Marcy, G. W.; Han, E.; Feng, Y.; Johnson, J. A.; Howard, A. W.; Fischer, D. A.; Valenti, J. A.; Anderson, J.; Piskunov, N. (2011). "The Exoplanet Orbit Database". Publications of the Astronomical Society of the Pacific. 123 (902): 412–42. arXiv:1012.5676. Bibcode:2011PASP..123..412W. doi:10.1086/659427. S2CID 51769219.
  68. ^ Terquem, C.; Papaloizou, J. C. B. (2007). "Migration and the Formation of Systems of Hot Super-Earths and Neptunes". The Astrophysical Journal. 654 (2): 1110–1120. arXiv:astro-ph/0609779. Bibcode:2007ApJ...654.1110T. doi:10.1086/509497. S2CID 14034512.
  69. ^ a b c Langford, P. M. (12 March 2012). "Transits of Venus". Astronomical Society of the Channel Island of Guernsey. Archived from the original on 11 January 2012. Retrieved 15 January 2016.
  70. ^ Bazsó, A.; Eybl, V.; Dvorak, R.; Pilat-Lohinger, E.; Lhotka, C. (2010). "A survey of near-mean-motion resonances between Venus and Earth". Celestial Mechanics and Dynamical Astronomy. 107 (1): 63–76. arXiv:0911.2357. Bibcode:2010CeMDA.107...63B. doi:10.1007/s10569-010-9266-6. S2CID 117795811.
  71. ^ a b Shortt, D. (22 May 2012). "Some Details About Transits of Venus". The Planetary Society. Retrieved 22 May 2012.
  72. ^ Rosenblatt, P.; Charnoz, S.; Dunseath, K. M.; Terao-Dunseath, M.; Trinh, A.; Hyodo, R.; Genda, H.; Toupin, S. (4 July 2016). "Accretion of Phobos and Deimos in an extended debris disc stirred by transient moons" (PDF). Nature Geoscience. 9 (8): 581–583. Bibcode:2016NatGe...9..581R. doi:10.1038/ngeo2742. S2CID 133174714.
  73. ^ Goffin, E. (2001). "New determination of the mass of Pallas". Astronomy and Astrophysics. 365 (3): 627–630. Bibcode:2001A&A...365..627G. doi:10.1051/0004-6361:20000023.
  74. ^ Kovacevic, A. B. (2012). "Determination of the mass of Ceres based on the most gravitationally efficient close encounters". Monthly Notices of the Royal Astronomical Society. 419 (3): 2725–2736. arXiv:1109.6455. Bibcode:2012MNRAS.419.2725K. doi:10.1111/j.1365-2966.2011.19919.x.
  75. ^ Taylor, D. B. (1982). "The secular motion of Pallas". Monthly Notices of the Royal Astronomical Society. 199 (2): 255–265. Bibcode:1982MNRAS.199..255T. doi:10.1093/mnras/199.2.255.
  76. ^ Goldreich, P. (1965). "An explanation of the frequent occurrence of commensurable mean motions in the solar system". Monthly Notices of the Royal Astronomical Society. 130 (3): 159–181. Bibcode:1965MNRAS.130..159G. doi:10.1093/mnras/130.3.159.
  77. ^ a b Chen, E. M. A.; Nimmo, F. (2008). "Thermal and Orbital Evolution of Tethys as Constrained by Surface Observations" (PDF). Lunar and Planetary Science XXXIX. Lunar and Planetary Institute. #1968. Retrieved 14 March 2008.
  78. ^ Murray, C. D.; Thompson, R. P. (1990). "Orbits of shepherd satellites deduced from the structure of the rings of Uranus". Nature. 348 (6301): 499–502. Bibcode:1990Natur.348..499M. doi:10.1038/348499a0. S2CID 4320268.
  79. ^ a b Tittemore, W. C.; Wisdom, J. (1990). "Tidal evolution of the Uranian satellites: III. Evolution through the Miranda-Umbriel 3:1, Miranda-Ariel 5:3, and Ariel-Umbriel 2:1 mean-motion commensurabilities". Icarus. 85 (2): 394–443. Bibcode:1990Icar...85..394T. doi:10.1016/0019-1035(90)90125-S. hdl:1721.1/57632.
  80. ^ a b Tittemore, W. C.; Wisdom, J. (1988). "Tidal Evolution of the Uranian Satellites I. Passage of Ariel and Umbriel through the 5:3 Mean-Motion Commensurability". Icarus. 74 (2): 172–230. Bibcode:1988Icar...74..172T. doi:10.1016/0019-1035(88)90038-3. hdl:1721.1/57632.
  81. ^ a b Zhang, K.; Hamilton, D. P. (2007). "Orbital resonances in the inner Neptunian system: I. The 2:1 Proteus–Larissa mean-motion resonance". Icarus. 188 (2): 386–399. Bibcode:2007Icar..188..386Z. doi:10.1016/j.icarus.2006.12.002.
  82. ^ a b Zhang, K.; Hamilton, D. P. (2008). "Orbital resonances in the inner Neptunian system: II. Resonant history of Proteus, Larissa, Galatea, and Despina". Icarus. 193 (1): 267–282. Bibcode:2008Icar..193..267Z. doi:10.1016/j.icarus.2007.08.024.
  83. ^ a b c d Matson, J. (11 July 2012). "New Moon for Pluto: Hubble Telescope Spots a 5th Plutonian Satellite". Scientific American. Retrieved 12 July 2012.
  84. ^ a b Ward, W. R.; Canup, R. M. (2006). "Forced Resonant Migration of Pluto's Outer Satellites by Charon". Science. 313 (5790): 1107–1109. Bibcode:2006Sci...313.1107W. doi:10.1126/science.1127293. PMID 16825533. S2CID 36703085.
  85. ^ a b c Ragozzine, D.; Brown, M. E. (2009). "Orbits and Masses of the Satellites of the Dwarf Planet Haumea=2003 EL61". The Astronomical Journal. 137 (6): 4766–4776. arXiv:0903.4213. Bibcode:2009AJ....137.4766R. doi:10.1088/0004-6256/137/6/4766. S2CID 15310444.
  86. ^ Hansen, K. (7 June 2004). "Orbital shuffle for early solar system". Geotimes. Retrieved 26 August 2007.
  87. ^ Tittemore, W. C. (1990). "Tidal heating of Ariel". Icarus. 87 (1): 110–139. Bibcode:1990Icar...87..110T. doi:10.1016/0019-1035(90)90024-4.
  88. ^ Tittemore, W. C.; Wisdom, J. (1989). "Tidal Evolution of the Uranian Satellites II. An Explanation of the Anomalously High Orbital Inclination of Miranda" (PDF). Icarus. 78 (1): 63–89. Bibcode:1989Icar...78...63T. doi:10.1016/0019-1035(89)90070-5. hdl:1721.1/57632.
  89. ^ Malhotra, R.; Dermott, S. F (1990). "The Role of Secondary Resonances in the Orbital History of Miranda". Icarus. 85 (2): 444–480. Bibcode:1990Icar...85..444M. doi:10.1016/0019-1035(90)90126-T.
  90. ^ Burns, J. A.; Simonelli, D. P.; Showalter, M. R.; Hamilton, D. P.; Porco, Carolyn C.; Esposito, L. W.; Throop, H. (2004). "Jupiter's Ring-Moon System" (PDF). In Bagenal, Fran; Dowling, Timothy E.; McKinnon, William B. (eds.). Jupiter: The Planet, Satellites and Magnetosphere. Cambridge University Press. ISBN 978-0-521-03545-3.

외부 링크