
길이 5의 S ={( 2,),( , ),( ,- )} {\
={( 2,),( , ),( ,- )} {\
In combinatorics, a lattice path  in
in  of length
of length  with steps in
with steps in  is a sequence
is a sequence  such that each consecutive차이 i- - 는 S {\S에 위치한다
such that each consecutive차이 i- - 는 S {\S에 위치한다
 [1] 격자 는 R {\{
[1] 격자 는 R {\{ [1]의 모든 격자에 위치할 수 있지만, 정수 격자 Z 이 가장 일반적으로 사용된다
[1]의 모든 격자에 위치할 수 있지만, 정수 격자 Z 이 가장 일반적으로 사용된다
An example of a lattice path in  of length 5 with steps in
of length 5 with steps in  is ( (), 2,- (
is ( (), 2,- ( 
북동 격자 경로
A North-East (NE) lattice path is a lattice path in  with steps in
with steps in  . The
. The  steps are called North steps and denoted by
steps are called North steps and denoted by  's; the 단계는
's; the 단계는 East step이라고 E
East step이라고 E  s로 표시된다.
s로 표시된다.
NE 격자 경로는 가장 일반적으로 출발지에서 시작한다.이 규칙을 통해 NE 격자 경로 에 대한 모든 정보를 단일 순열 단어로 인코딩할 수 있다.단어의 길이는 격자 경로의 단계 수인 를 알려준다
인코딩할 수 있다.단어의 길이는 격자 경로의 단계 수인 를 알려준다
 s와 의
s와 의 는 L }의 순서를 전달하며
는 L }의 순서를 전달하며 나아가 단어에 된 N N의
나아가 단어에 된 N N의 수와 E의 가
수와 E의 가 L의 끝점을 결정한다
L의 끝점을 결정한다
NE 격자 경로에 순열 단어가 n 와
 e
e  및 단계에
및 단계에 포함된 경우, 경로가 원점에서 시작되면 반드시( , ) 에서 종료된다
포함된 경우, 경로가 원점에서 시작되면 반드시( , ) 에서 종료된다 이는 정확히 을 "걸음"했기 때문이다. 계단
이는 정확히 을 "걸음"했기 때문이다. 계단 과 e{\}계단
과 e{\}계단 동쪽 계단은(,0) 단계
동쪽 계단은(,0) 단계

정확히 하나의 {\ N 및 3개의 s로 (0
및 3개의 s로 (0
 ) )부터 격자 경로.엔드포인트는 반드시 ( ) 3 에 있다
) )부터 격자 경로.엔드포인트는 반드시 ( ) 3 에 있다
격자 경로 계산
격자 경로는 종종 다른 결합 물체를 세는 데 사용된다.마찬가지로 특정 종류의 격자 경로의 수를 세는 결합 물체가 많다.이것은 격자 경로가 문제의 물체와 편향되었을 때 발생한다.예를 들어,
- Dyck paths are counted by the
 Catalan number
Catalan number  . A Dyck path is a lattice path in
. A Dyck path is a lattice path in  from
from  to
to  with steps in ) -축
with steps in ) -축 아래로 절대 지나가지 않는
아래로 절대 지나가지 않는 [2]}동등하게, Dyck 경로는( ) 에서
[2]}동등하게, Dyck 경로는( ) 에서 ) 까지의 NE 격자 경로로서
) 까지의 NE 격자 경로로서 , y = {\y= 아래에 완전히 놓여 있다
, y = {\y= 아래에 완전히 놓여 있다 [2][3]
[2][3] - The Schröder numbers count the number of lattice paths from
 to
to  with steps in
with steps in  and
and  that never rise above the diagonal
that never rise above the diagonal  .[2]
.[2] - , ) 에서
 (, ) 까지의
(, ) 까지의 NE 격자 경로 수는+ {\
NE 격자 경로 수는+ {\  집합에서 a의 조합 수를 카운트한다
집합에서 a의 조합 수를 카운트한다 .
.
조합 및 NE 격자 경로
NE 격자경로는 이항계수에 의해 계수되고 파스칼의 삼각형으로 배열된 조합의 수와 밀접한 연관성을 가진다.아래 도표는 이러한 연결의 일부를 보여준다.
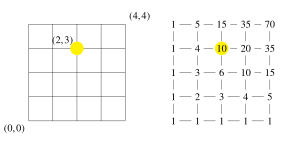
) 에서 () 까지의 격자 경로 수는( )= ( ) = {\{\}과 동일함
() 까지의 격자 경로 수는( )= ( ) = {\{\}과 동일함
 .
. , ) 에서 (, ) 까지의 격자 경로 수는 이항 계수+ ) {과
(, ) 까지의 격자 경로 수는 이항 계수+ ) {과 같다
같다 The diagram shows this for
The diagram shows this for  . If one rotates the diagram 135° clockwise about the origin and extend it to include all
. If one rotates the diagram 135° clockwise about the origin and extend it to include all  , one obtains Pascal's triangle.파스칼 삼각형의 n} 행의
, one obtains Pascal's triangle.파스칼 삼각형의 n} 행의
 {\displaystyle n^{\ 항목이 이항 계수( {\
{\displaystyle n^{\ 항목이 이항 계수( {\ 이기 때문에 이 결과는 놀랄 일이 아니다.
이기 때문에 이 결과는 놀랄 일이 아니다.
문제 및 증거
NE 격자 경로의 그래픽 표현은 결합을 수반하는 많은 주관적 증거에 도움이 된다.여기 몇 가지 예가 있다.
- = ( ) 2=( ) n}{\

Proof: The right-hand side is equal to the number of NE lattice paths from  to
to  . Each of these NE lattice paths intersects exactly one of the lattice points in the rectangular array with coordinates
. Each of these NE lattice paths intersects exactly one of the lattice points in the rectangular array with coordinates  for
for  에 대해 아래 에 표시된 와 같이,() {\
에 대해 아래 에 표시된 와 같이,() {\ (에서 )까지
(에서 )까지 모든NE 격자 경로는 색상 노드 중 정확히 하나를 교차한다
모든NE 격자 경로는 색상 노드 중 정확히 하나를 교차한다 .
.

각 NE 격자 경로는 정확히 하나의 컬러 노드를 통과한다. 왼쪽에서 이항계수 제곱 ) 은 시작점에 부착된
시작점에 부착된 (, 0) {\ (에서
(, 0) {\ (에서 - ) 까지 NE 격자 경로 집합의 두 개를 나타낸다.두 번째 사본을 시계 방향으로 90° 돌리십시오.이렇게 해도 개체의 조합은 변경되지 않는다.( k)= ( - ) binom
- ) 까지 NE 격자 경로 집합의 두 개를 나타낸다.두 번째 사본을 시계 방향으로 90° 돌리십시오.이렇게 해도 개체의 조합은 변경되지 않는다.( k)= ( - ) binom  따라서 격자 경로의 총 수는 그대로 유지된다.
따라서 격자 경로의 총 수는 그대로 유지된다.

두 번째 복사본이 시계 방향으로 90° 회전한 상태에서 제곱된 NE 격자 경로 세트. 아래 그림과 같이 동일한 직사각형 배열 위에 제곱된 NE 격자 경로를 겹친다., ) 에서 (, ) 까지의 모든 NE 격자 경로가 설명되어 있음을
(, ) 까지의 모든 NE 격자 경로가 설명되어 있음을 알 수 있다.특히 적색 격자점을 통과하는 격자 경로(예를 들어)는 격자 경로의 제곱 집합(적색으로도 표시됨)에 의해 계산된다는 점에 유의하십시오.
알 수 있다.특히 적색 격자점을 통과하는 격자 경로(예를 들어)는 격자 경로의 제곱 집합(적색으로도 표시됨)에 의해 계산된다는 점에 유의하십시오.
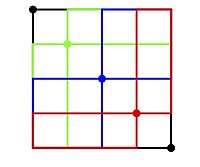
겹쳐진 NE 격자 경로 세트 제곱.모든 NE 격자 경로가 설명된다. 참조
































 NE 격자 경로 수는
NE 격자 경로 수는
 .
.


 같다
같다

















