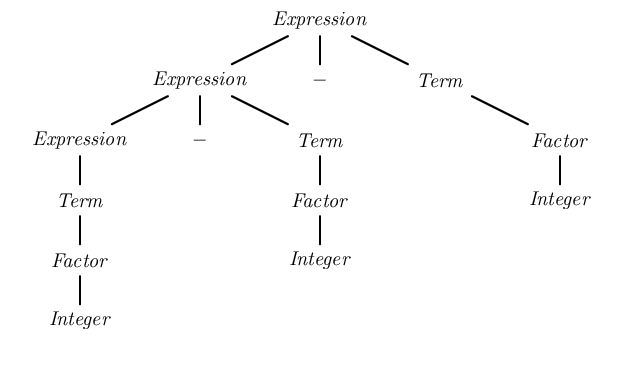
좌측 재귀

이 글은 대부분의 독자들이 이해하기에는 너무 기술적인 것일 수도 있다. 기술 세부 정보를 삭제하지 않고 비전문가가 이해할 수 있도록 개선하십시오.(2015년 11월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

컴퓨터 과학의 형식 언어 이론에서 좌뇌 재귀는 그 같은 언어(왼쪽)에서 끈으로 분해되는 것과 접미사(오른쪽)로 분해되는 것에 의해 현이 언어의 일부로 인식되는 특수한 재귀 사례다.예를 들어,${\displaystyle }1{\displaystyle \mathrm{}}$ +${\displaystyle 2}$ + 3 ${\displaystyle$1+$2$$+3}$은(는)${\displaystyle }$1 + ${\displaystyle 2}${\$displaystyle 1+$2$\},$ 또한${\displaystyle }$합과 ${\displaystyle \mathrm{적절한}}$접미사인 + 3 {\displaystyle ${}+3}$로 나눌 수 있기 때문에 합으로 인식할 수 있다$$.

문맥이 없는 문법의 관점에서, 비단어적 문법은 그 제작물 중 하나에서 가장 왼쪽의 기호가 그 자체이거나(직접 왼쪽 재귀의 경우) 어떤 순서로 대체될 수 있는 경우(간접 왼쪽 재귀의 경우)에 의해 스스로 만들어질 수 있는 경우에 왼쪽-재귀가 된다.

정의

문법은 자신을 가장 왼쪽 기호로 하여 보초적 형태로 유도할 수 있는$$ 비터미널 $기호{\displaystyle }$ A ${\displaystyle A}$이(가) 있는 경우에만 왼쪽 반복된다.^[1]상징적으로

${\displaystyle A}$ ${\displaystyle {}^{}}$+ ${\displaystyle {}^{}}$ ${\displaystyle \alpha }$ ${\displaystyle A\Rightarrow ^{+}A\alpha$ $\},$

여기서 $\Rightarrow {\displaystyle {}^{}}$+ ${\$는 하나 이상의 대체품을 만드는 작업을 나타내며$$, $\alpha {\displaystyle }$ ${\displaystyle \alpha }$은(는) 단자와 비단자 기호의 모든 시퀀스다$$.

좌측 직진 재귀

왼쪽의 직접적인 재귀는 정의가 하나의 대체만으로 충족될 수 있을 때 발생한다.그것은 형식상의 규칙을 필요로 한다.

$A\to A\alpha }$

여기서 $\alpha {\displaystyle }$ ${\displaystyle \alpha }$은(는) 비터미널 및 단자의 시퀀스 입니다.예를 들어 규칙

${\displaystyle {\mathit {Expression}\to {\mathit}+{\mathit {Term}}$

직접 좌회귀적이야이 규칙에 대한 왼쪽에서 오른쪽으로의 재귀 하강 파서가

공허하게 하다 표현() {   표현();   짝을 맞추다('+');   용어(); } 

그리고 그러한 코드는 실행될 때 무한 재귀에 속할 것이다.

간접 좌측 재귀

간접 좌회전 재회귀는 여러 가지 대체물을 통해 좌회전의 정의가 충족될 때 발생한다.그것은 그 패턴을 따르는 일련의 규칙을 수반한다.

${\displaystyle A_{0}\to \beta _{0}A_{1}\알파 _{0}}}$

${\displaystyle A_{1}\to \beta _{1}A_{2}\alpha _{1}:{1}}$

$\displaystyle \cdots }$

$\beta _{n}\to \beta _{n}A_{0}\알파 _{n}}$

where ${\displaystyle \beta _{0},\beta _{1},\ldots ,\beta _{n}}$ are sequences that can each yield the empty string, while ${\displaystyle \alpha _{0},\alpha _{1},\ldots ,\alpha _{n}}$ may be any sequences of terminal and nonterminal symbols at all.이러한 시퀀스는 비어 있을 수 있다는 점에 유의하십시오.파생

${\displaystyle A_{0}\Rightarrow \beta _{0}A_{1}\alpha _{0}\Rightarrow ^{+}A_{1}\alpha _{0}\Rightarrow \beta _{1}A_{2}\alpha _{1}\alpha _{0}\Rightarrow ^{+}\cdots \Rightarrow ^{+}A_{0}\alpha _{n}\dots \alpha _{1}\alpha _{0}}$

그런 다음, $A$에게 마지막 보초적 형태에서 가장 왼쪽처럼$$ ${\$을 부여한다.

왼쪽 재귀 제거

왼쪽 재귀는 (대부분의 하향식 파서의 경우처럼) 무한 재귀로 유도하기 때문에 또는 (CYK 알고리즘을 포함한 많은 상향식 파서의 경우처럼) 그것을 금지하는 정상적인 형태의 규칙을 기대하기 때문에 파서들에게 종종 문제를 제기한다.그러므로 문법은 종종 왼쪽 재귀들을 없애기 위해 사전 처리된다.

좌측 직접 재귀 제거

좌측 직진 재귀 제거에 대한 일반 알고리즘은 다음과 같다.이 방법에는 몇 가지 개선이 이루어졌다.^[2]왼쪽-복구 $비터미네랄{\displaystyle }$ A ${\displaystyle A$의 경우${\displaystyle ,}$ ${\displaystyle A}$ → A$$→ {\$displaystyle A\오른쪽$화살표 A} 형식의 규칙을 취소하고$$ 남아 있는 규칙을 고려하십시오.

${\displaystyle A\wrightarrow A\alpha _{1}\mid \ldots \mid \ldots \mid \ldots \{1}\mid \ldots \mid \beta _{m}}}}}$

여기서:

• 각 $\alpha {\displaystyle }$ ${\displaystyle \alpha}$은(는) 비터미널 및 단자의 비어 있지 않은 시퀀스이며,
• 각 $\beta {\displaystyle }$ ${\displaystyle \beta }$은(는) A ${\displaystyle A}$로 시작하지 않는 비터미널 및 단자의 시퀀스입니다$.$

$다음{\displaystyle }$ 두 세트의$$프로덕션(A {\displaystyle $A}$에 대해 한 세트)으로 대체하십시오$.$

${\displaystyle A\rightarrow \beta \{1}A^{\premium \ldots \mid \beta _{m}A^{\prime }}$

그리고 새로운 비터미널 $A{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\$흔히 "꼬리" 또는 "휴지"라고 함)$$을 위한 또 다른 세트:

$\displaystyle A^{\premy }\오른쪽 화살표 \alpha \{1}A^{\premy \ldots \mid \ldots \mid \nalpha _{n}A^{\primy }\mid \epsilon }}}}}$

좌측 직접적인 재귀가 남아 있지 않을 때까지 이 프로세스를 반복하십시오.

예를 들어 규칙 집합을 고려하십시오.

${\displaystyle {\mathit {Expression}\오른쪽 화살표 {Expression}+{\mathit {Expression}\mid {\mathit {Integer}\mid {\mathit {String}}}}$

이것은 다음과 같이 왼쪽 재귀가 반복되지 않도록 다시 쓰여질 수 있다.

${\displaystyle {\mathit {Expression}\오른쪽 화살표 {\mathit {Integer}\,{\mathit {Expression}}, {\mathit {String}\,{\mathit {Expression}}}}}$

${\displaystyle {\mathit {Expression}'\오른쪽 화살표 {}+{\mathit {Expression}\,{\mathit {Expression}}}\mid \epsilon }}$

모든 좌측 재귀 제거

비터미널에 대한 위상학적 순서를 설정함으로써, 위의 프로세스를 확장하여 간접적인 좌측 재귀도^{[citation needed]} 제거할 수 있다.

입력 문법: ${\displaystyle {비단어\mathrm{}}_{}}$ A $1{\displaystyle {}_{}}$,${\displaystyle \dots ,}$ ${\displaystyle n_{}}${\$displaystyle A_{1},\ldots, A_{n}$ 및 그$$ 제작물 세트

출력 동일한 언어를 생성하지만 반복되지 않는 수정된 문법

1. 각 비터미널 ${\displaystyle A_{}}$ i ${\$에 대해 $:$
   1. 반복해서 문법을 변경하지 않을 때까지 반복하십시오.
      1. 각 규칙 $A{\displaystyle {}_{}}$ ${\displaystyle i_{}}$→ ${\displaystyle {\alpha }_{}}$ i ${\$ 화살표 $\alpha _{i$ $\alpha {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$은(는) 단자 및 비단자 순서:
         1. $\alpha {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$이(가) 비터미널 $A$ j ${\$ 및 < i ${\displaysty$ j<$i$ :
            1. $선행$ $A{\displaystyle {}_{}}$ ${\displaystyle j_{}}$ ${\$ $\beta_{i}$를 사용하지$$ 않고 $\alpha {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$${i}$이 되도록 한다$.$
            2. 규칙 $A{\displaystyle {}_{}}$ ${\displaystyle i_{}}$→ ${\displaystyle {\alpha }_{}}$ i ${\$ 화살표 $\알파 _{i}}$을(를) 제거하십시오$.$
            3. 각 규칙 $A{\displaystyle {}_{}}$ ${\displaystyle j_{}}$→ ${\displaystyle {\alpha j}_{}}$ ${\$오른쪽 $화살표 \알파 _{j}}$:
               1. 규칙 $A{\displaystyle {}_{}}$ ${\displaystyle i_{}}$→ ${\displaystyle {\alpha j}_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle i_{}}$ ${\$ 화살표 $\알파 _{j}\베타 _{i}}$을(를) 추가한다$.$
   2. 위에서 설명한 대로$$ $A{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$에 대한 직접 좌측 재귀는 제거하십시오.

이 알고리즘은 비터미널 순서에 매우 민감하다는 점에 유의하십시오. 최적화는 종종 이 순서를 잘 선택하는 데 초점을 맞춘다.^{[clarification needed]}

함정스

위의 변화들은 문법에 의해 생성된 언어를 보존하지만, 그들은 현악의 인식을 목격하는 파스 트리를 바꿀 수도 있다.적절한 부기를 갖추면 나무 재작성이 원형을 회복할 수 있지만, 이 단계를 생략하면 그 차이가 파스의 의미론을 바꿀 수도 있다.

연관성은 특히 취약하다. 왼쪽 연관 연산자는 일반적으로 새로운 문법에 따라 오른쪽 연관성 같은 배열로 나타난다.예를 들어, 다음 문법부터 시작하십시오.

${\displaystyle {\mathit {Expression}\오른쪽 화살표 {\mathit {Expression}\,-\,{\mathit {Term}\mid {\mathit {Term}}}$

${\displaystyle {\mathit {Term}\오른쪽 화살표 {\mathit {Termat}\,*\,{\mathit {Factor}\mid {\mathit {Factor}}}$

${\displaystyle {\mathit {Factor}\오른쪽 화살표({\mathit {Expression}})\mid {\mathit {Integer}}}$

왼쪽 재귀 제거를 위한 표준 변환은 다음을 산출한다.

${\displaystyle {\mathit {Expression}\오른쪽 화살표 {\mathit {Term}\\mathit {Expression}}}$

${\displaystyle {\mathit {Expression}'\오른쪽 화살표 {}-{\mathit {Term}\\mathit {Expression}}\mid \epsilon }}$

${\displaystyle {\mathit {Term}\오른쪽 화살표 {\mathit {Factor}\ {\mathit {Term}}}$

${\displaystyle {\mathit {Term}\오른쪽 화살표 {}*{\mathit {Factor}\{\mathit {Term}}\mid \엡실론}}$

${\displaystyle {\mathit {Factor}\오른쪽 화살표({\mathit {Expression}})\mid {\mathit {Integer}}}$

LALR 파서의 첫 번째 문법과 함께 "1 - 2 - 3" 문자열을 파싱하면 파스 트리가 생성될 것이다.

이 파스 트리는 왼쪽의 용어를 그룹화하여 정확한 의미론(1 - 2) - 3을 제시한다.

두 번째 문법으로 파싱하면 얻을 수 있다.

적절히 해석하면 1 + (-2 + (-3)도 맞지만 입력에 충실하지 않고 일부 운영자는 구현하기가 훨씬 어렵다.오른쪽의 용어는 오른쪽의 문법이 1 - (2 - 3)로 배열되듯이 나무의 깊숙한 곳에 어떻게 나타나는지 주목하라.

하향식 구문 분석에서 왼쪽 재귀 수용

왼쪽 재귀가 포함된 공식 문법은 약하게 등가되는 오른쪽 재귀 형식으로 변환되지 않는 한 LL(k)-파서 또는 기타 순진한 재귀적 하강 파서(parcer)로 구문 분석할 수 없다.반면 왼쪽 재귀는 오른쪽 재귀보다 스택 사용량이 낮기 때문에 LALR 파서에게는 왼쪽 재귀가 선호된다.그러나 보다 정교한 하향식 파서들은 축소를 사용하여 일반적인 상황 없는 그래머를 구현할 수 있다.2006년에 프로스트와 하피즈는 왼쪽-복귀 직접 생산 규칙을 가진 모호한 문법을 수용하는 알고리즘을 기술했다.^[3]이 알고리즘은 2007년 프로스트, 하피즈, 캘러헌에 의한 매우 모호한 그래머에 대해 간접적인 것은 물론 직접적인 왼쪽 재귀까지 수용하기 위해 완전한 파싱 알고리즘으로 확장되었고 잠재적으로 기하급수적으로 많은 파스 트리의 파스 트리의 수를 콤팩트하게 표현하기 위해 확장되었다.^[4]그 후 저자들은 이 알고리즘을 하스켈 프로그래밍 언어로 작성된 파서 콤비네이터 세트로 구현했다.^[5]

참고 항목

• 꼬리재순환

참조

외부 링크

• LALR(1) 그래머의 실제 고려사항