키르흐호프의 정리

그래프 이론의 수학 분야에서는 구스타프 키르흐호프의 이름을 딴 키르흐호프의 정리나 키르흐호프의 행렬 트리 정리는 그래프에 있는 스패닝 나무의 수에 대한 정리로서, 이 숫자는 그래프의 라플라시안 행렬의 하위트릭스의 결정인자로부터 다항 시간 단위로 계산할 수 있음을 보여준다. 구체적으로는 그 수는 e이다.라플라시안 매트릭스의 모든 공동 인자(co factor)에 적합하다.키르흐호프의 정리는 완전한 그래프로 스패닝 나무의 수를 제공하는 케이리 공식의 일반화다.

Kirchhoff의 정리는 그래프의 도 행렬(대각선상에 정점도가 있는 대각선 행렬)과 정점이 인접해 있고 그렇지 않으면 0이 되는 위치에서 1이 있는 인접 행렬(a (0,1) 매트릭스)의 차이와 동일한 그래프의 라플라크 행렬의 개념에 의존한다.

정점이 n개인 연결된 그래프 G의 경우, λ₁, λ₂, ..., λ은_n−1 라플라시안 행렬의 0이 아닌 고유값이 되도록 한다.그러면 G의 스패닝 나무의 수는

${\displaystyle t(G)={\frac {1}{n}\lambda _{1}\lambda _{2}\cdots \lambda _{n-1}\,}$

매트릭스-트리 정리를 사용한 예

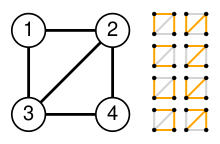
먼저 다이아몬드 그래프 G의 예에 대한 라플라시안 행렬 Q를 생성하십시오(오른쪽 이미지 참조).

${\displaystyle Q=\왼쪽[{\begin{array}{rrr}2&-1&-1&0\\-1&3&-1&-1\\1&1&3-1\\#1&1&1&2\end{array}\right}.}$

다음으로 Q에서 행과 열을 삭제하여 행렬 Q를^* 생성한다.예를 들어, 1행 및 1열 산출물 삭제

${\displaystyle Q^{\ast }=\왼쪽[{\begin{array}{rrr}3&-1&-1\\-1&3&-1\\\-1&1&2\nd{array}\rigin}\rigin}\rigin}\right].}$

마지막으로 Q의^* 결정인자를 취하여 다이아몬드 그래프의 경우 8인 t(G)를 구한다. (이 예에서는 공지 t(G)가 Q의 (1,1)-coactor이다.)

증명 개요

(아래 증명은 카우치-비넷 공식에 근거한다.키르흐호프의 정리를 위한 기본적인 유도 논거는 무어 654페이지(2011년)에서 찾을 수 있다.^[1]

첫 번째 주의: 라플라크 행렬은 모든 행과 열에 걸쳐 입력된 값의 합이 0인 속성을 가지고 있다.따라서 행과 열을 추가하고 전환하며 행이나 열에 -1을 곱하여 모든 부문을 다른 부조로 변환할 수 있다.따라서 공동 작용자는 서명하기 위해 동일하며, 실제로 동일한 기호를 가지고 있음을 확인할 수 있다.

우리는 계속해서 마이너 M의₁₁ 결정인자가 스패닝 나무의 수를 세는 것을 보여준다.n은 그래프의 꼭지점 수로 하고, m은 그래프의 가장자리 수로 한다.발생 행렬 E는 n-by-m 행렬로, 다음과 같이 정의할 수 있다: (i, j)가 그래프의 k번째 에지이고, i < j를 가정한다.그런_ik 다음 E = 1, E = -1_jk 및 k 열의 다른 모든 항목은 0이다(이 수정된 발생 행렬 E를 이해하려면 지향적 발생 행렬 참조).앞의 예(n = 4 및 m = 5):

${\displaystyle E={\begin{bmatrix}1&0&0&0&0&0\\1&0&1&0\\0&0&0&1\\nd{bmatrix}.}$

Laplacian L은 발생 매트릭스와 그 전치(즉, L = EE^T)의 곱에 인수될 수 있다는 점을 상기하십시오.또한 FF^T = M이₁₁ 되도록 F는 첫 번째 행이 삭제된 행렬 E가 되도록 한다.

이제 Cauchy-Binet 공식은 우리가 글을 쓸 수 있게 해준다.

${\displaystyle \reft(M_{11}\right)=\sum \{S}\det \reft(F_{S}\right)\det \left(F_{S}^{S}^{S}}\sum \{S}\det \refteput{{{{{{{S}}}}^2}}$

여기서 S는 크기가 n - 1인 [m]의 하위 집합에 걸쳐 있고, F는_S (n - 1) by by(n - 1) 행렬을 나타내며, 열은 S에 인덱스가 있는 F 행렬이다.그리고 모든 S는 원래 그래프의 n - 1 가장자리를 지정하며, F의_S 결정인자가 +1 또는 -1인 경우에만 그러한 가장자리가 스패닝 트리를 유도하고, 결정인자가 0인 경우에는 스패닝 트리를 유도하지 않는다는 것을 알 수 있다.이것으로 증거가 완성되었다.

특정 사례 및 일반화

케이리 공식

케일리의 공식은 특별한 경우로서 키르흐호프의 정리로부터 따르며, 왜냐하면 한 곳에 1이 있고, 다른 곳에 -1이 있고, 다른 곳에 0이 있는 모든 벡터는 완전한 그래프의 라플라시안 행렬의 고유 벡터로서 해당 고유값은 n이 되기 때문이다.이러한 벡터는 차원 n - 1의 공간에 걸쳐 있으므로 0이 아닌 다른 고유값은 없다.

또는 Cayley의 공식은 완전한 그래프 K의_n 구별되는 라벨링된 나무의 수를 셀 때 우리는 K의_n 라플라크 행렬의 어떤 공동 인자라도 계산해야 한다는 점에 주목하라.이 경우 라플라크 행렬은

$#\displaystyle {\bmatrix}n-1&#1&\cdots &-1\\1\1&n-1&\cdots &\nd{bmatrix}.}$

위의 매트릭스의 모든 공작용자는 n인데ⁿ⁻², 이것은 케이리의 공식이다.

키르흐호프의 다문 정리

Kirchhoff의 정리에는 다중 글씨도 포함되어 있다. 행렬 Q는 다음과 같이 수정된다.

• 항목 q는_i,j -m이며, 여기서 m은 i와 j 사이의 가장자리 수입니다.
• 정점의 정도를 계산할 때 모든 루프는 제외된다.

Cayley의 완전한 다중 글씨를 위한 공식은 m = 1의 다중 글씨를 가진 단순한 그래프이기 때문에 위에서 생산한 동일한 방법으로 m^n-1(n-^n-1(n-1)n이다^n-2.

스패닝 트리의 명시적 열거

키르호프의 정리는 라플라크 행렬의 정의를 변경함으로써 강화될 수 있다.단순히 각 꼭지점에서 발산되는 가장자리를 세거나 한 쌍의 꼭지점을 연결하기 보다는 각 가장자리에 미확정으로 라벨을 붙이며, 수정된 라플라크 행렬의 (i, j)번째 항목이 j가 같지 않을 때 i번째와 j번째 꼭지점 사이의 가장자리에 해당하는 미결정체 위의 합이고, 음의 합은 모든 인디미터에 대한 합이 되도록 한다.i가 j일 때 i번째 꼭지점에서 나오는 가장자리에 해당하는 Minate.

위의 행과 열을 모두 삭제하여 수정된 라플라크 행렬의 결정인자는(원래 라플라크 행렬에서 스패닝 트리 수를 찾는 것과 유사), 그래프의 가장자리에 해당하는 인디테터미네이트에서 균일한 다항식(Kirchhoff 다항식)이다.항을 수집하고 가능한 모든 취소를 수행한 후, 결과 표현식의 각 모노미알은 해당 모노미알에 나타나는 불변수에 해당하는 가장자리로 구성된 스패닝 트리를 나타낸다.이렇게 하면 단순히 결정인자를 계산하는 것만으로 그래프의 모든 신장 트리를 명시적으로 열거할 수 있다.

매트로이드

그래프의 스패닝 트리는 그래픽 매트로이드의 베이스를 형성하므로 키르흐호프의 정리는 그래픽 매트로이드의 베이스 수를 셀 수 있는 공식을 제공한다.또한 그래픽 매트로이드의 일반화(Maurer 1976년)인 일반 매트로이드의 베이스 수를 계산할 때도 동일한 방법을 사용할 수 있다.

지시된 다중 글씨에 대한 키르쇼프의 정리

키르호프의 정리는 지시된 다중 글자에 있는 방향 스패닝 나무의 수를 세도록 수정할 수 있다.행렬 Q는 다음과 같이 구성된다.

• 구별 i와 j에 대한 항목 q는_i,j -m이며, 여기서 m은 i에서 j까지의 에지 수입니다.
• 항목 q는_i,i i의 외설적인 숫자에서 i의 루프 수를 뺀 값이다.

i 정점에 뿌리를 둔 방향 스패닝 트리의 수는 i번째 행과 Q 열을 제거하여 얻은 행렬의 결정 요인이다.

k-구성 요소 포리스트에 걸친 카운트

Kirchhoff의 정리를 일반화하여 비가중 그래프에 k 성분 스패닝 숲을 계수할 수 있다.^[2]k-구성 요소 스패닝 포리스트는 모든 정점을 포함하고 주기가 없는 k-연결 구성요소를 가진 하위 그래픽이다. 즉, 각 정점 쌍 사이에 최대 하나의 경로가 있다.Given such a forest F with connected components ${\textstyle F_{1},\dots ,F_{k}}$, define its weight ${\textstyle w(F)= V(F_{1}) \cdot \dots \cdot V(F_{k}) }$ to be the product of the number of vertices in each component.그러면

${\displaystyle \sum _{F}w(F)=q_{k},}$

여기서 합계는 모든 k-구성 요소 스패닝 포리스트에 걸쳐 있고 $q_{}${\$textstyle q_{k}}}$은 다항식의$$ $x{}^{}$ $k^{}$ ${\$ x$^{k}}$의 계수다.

${\displaystyle(x+\data _{1})\reason(x+\data _{n-1}x.}$

다항식의 마지막 인자는 0 고유값 $\mathrm{\lambda n}{}_{}$= 0 ${\textstyle \lambda _{n}=0}$에 기인한다$.$ 보다 명시적으로 $숫자{}_{}$ $q_{}$ k$${\$textstyle q_{k$}}}를 다음과 같이 계산할 수 있다$$.

${\displaystyle q_{k}=\sum _{{i_{1},\i_{n-k}\}\cHB\{1\i_{n-k}}\cHB \i_{1}}\i_{n-k}}}}$

여기서 합계는$${$1$,$$… , $n\}$ ${\textstyle \{1,\dots,n$의 모든 n–k-element 하위 집합에 걸쳐 있다. 예를 들어,

${\displaystyle{\begin{정렬}q_{n-1}&, =\lambda _{1}+\dots +\lambda _{n-1}=\mathrm{tr}Q=2 E\\q_{n-2}&, =\lambda _{1}\lambda _{2}+\lambda _{1}\lambda _{3}+\dots +\lambda _{n-2}\lambda _{n-1}\\q_{2}&, =\lambda _{1}\dots _{n-3}\lambda _{n-1}+\dots +\lambda _{2}\dots \lambda _{n-1}\\q_{1}& \lambda, =\lambda _{n-2}+\lambda _{1}\dots \lambda._{1}\dots \lambda _{n1}\\end{aigned}}$

n–1 성분이 있는 스패닝 포리스트는 단일 에지에 해당하므로 k = n – 1 사례에 따르면 Q의 고유값 합계가 에지 수의 두 배라고 한다.k = 1 케이스는 모든 신장 트리의 무게가 n이기 때문에 원래의 키르흐호프 정리에 해당한다.

그 증거는 키르흐호프의 정리 증명과 유사하게 행해질 수 있다.발생 매트릭스의 반전성$(n$- $k$) $\times$( n$$- k$$) ${\textstyle (n-k)\times (n-k)}$ 서브트릭스는$$ 각 구성 요소에 대한 꼭지점을 선택할 수 있는 k-구성 요소 스패닝 포리스트에 생물적으로 대응한다.

계수 ${\$는 Q의 특성 다항식 계수에 서명하기 위해 위와$$ 같다.

참고 항목

• 프뤼퍼 수열
• 최소 스패닝 트리
• 나무 관련 주제 목록

참조

• Harris, John M.; Hirst, Jeffry L.; Mossinghoff, Michael J. (2008), Combinatorics and Graph Theory, Undergraduate Texts in Mathematics (2nd ed.), Springer.
• Maurer, Stephen B. (1976), "Matrix generalizations of some theorems on trees, cycles and cocycles in graphs", SIAM Journal on Applied Mathematics, 30 (1): 143–148, doi:10.1137/0130017, MR 0392635.
• Tutte, W. T. (2001), Graph Theory, Cambridge University Press, p. 138, ISBN 978-0-521-79489-3.
• Chaiken, S.; Kleitman, D. (1978), "Matrix Tree Theorems", Journal of Combinatorial Theory, Series A, 24 (3): 377–381, doi:10.1016/0097-3165(78)90067-5, ISSN 0097-3165

외부 링크

• 키르흐호프의 정리 증명