멤브레인 컴퓨팅

멤브레인 컴퓨팅(또는 MC)은 특히 세포막의 생물학적 세포 연구로부터 새로운 연산 모델을 발견하고자 하는 컴퓨터 과학 내의 영역이다.그것은 세포 모델을 만드는 하위 작업이다.null

멤브레인 컴퓨팅은 분산 및 병렬 컴퓨팅 모델을 다루며, 기호 객체의 멀티셋을 현지화 방식으로 처리한다.그러므로 진화 법칙은 진화하는 물체를 막에 의해 정의된 구획으로 캡슐화할 수 있게 한다.구획과 환경과의 통신은 그 과정에서 필수적인 역할을 한다.다양한 형태의 막 시스템은 1998년 이 모형을 처음 구상한 게오르게 푸룬 이후 P계통으로 알려져 있다.^[1]null

P계통의 필수 성분은 세포처럼 세포막의 계층적 배열이나 조직이나 신경망에서처럼 막의 그물(그래프의 노드에 위치)이 될 수 있는 그물막 구조다.P 시스템은 종종 그림과 함께 그래픽으로 묘사된다.null

아홉 지역 막 컴퓨터

막이라는 개념 뒤에 숨겨진 직관은 생물학에서 나온 3차원 방광이다.그러나 개념 자체가 더 일반적이며, 막은 두 지역의 분리막으로 보인다.그 막은 두 지역 사이의 선택적 의사소통을 제공한다.게오르게 푸룬에 따르면, 분리는 유한한 "내부"와 무한의 "외부"로 유클리드 공간을 이룬다.선택적 의사소통은 컴퓨팅이 들어오는 곳이다.null

그래픽 표현은 연구 중인 모델의 변동에 따라 수많은 요소를 가질 수 있다.예를 들어 규칙이 특수 기호 Δ를 생성할 수 있는데, 이 경우 규칙이 포함된 막이 용해되고 모든 내용이 지역 계층 구조에서 위로 이동한다.null

막 기반 멀티셋 처리 장치의 구조와 기능을 정의하는 생물학으로부터의 다양한 제안과 가능성의 범위는 사실상 무궁무진하다.실제로 멤브레인 계산 문헌에는 매우 많은 수의 모델이 포함되어 있다.따라서 MC는 단순히 특정 모델과 관련된 이론이 아니라 구획화된 모델을 고안하기 위한 틀이다.null

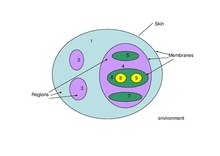
화학 물질은 기호에 의해 또는 기호의 줄에 의해 모델링된다.막에 의해 정의되는 부위는 다른 기호나 끈(집단적으로 물체라고 하는 것)이나 다른 막을 포함할 수 있으므로, P 시스템은 피부막이라고 하는 하나의 외막을 정확히 가지고 있으며, 피부막 아래에 있는 모든 그것의 막을 지배하는 위계적 관계를 가지고 있다.null

만약 물체가 기호라면, 지역 내에서 그 물체의 다중성이 중요하다; 그러나 다중 집합은 일부 문자열 모델에서도 사용된다.지역은 물체가 생성, 소비, 다른 지역으로 전달되는 방법을 정의하는 관련 규칙을 가지고 있다.시스템 전체에 걸쳐 규칙을 최대로 병렬로 적용하는 비결정론적 적용은 시스템 상태간의 전환이며, 일련의 전환을 연산이라고 한다.특정 목표는 정지 상태를 나타내기 위해 정의될 수 있으며, 이 시점에서 계산 결과는 특정 영역에 포함된 물체가 될 것이다.또는 피부막에서 환경으로 보내는 물체로 결과를 구성할 수도 있다.null

많은 변종 모델들이 연구되어 왔으며, 부울 만족도(SAT) 문제, 여행 세일즈맨 문제(TSP)와 같은 NP 완성 문제를 해결하기 위한 목적으로 소수의 막이 있는 시스템에 대한 계산 보편성 입증에 관심이 집중되어 왔다.P 시스템은 공간과 시간의 복잡성을 교환할 수 있으며 살아있는 세포의 자연 과정을 설명하기 위해 모델을 덜 사용하는 경우가 있다.그 연구는 적어도 이론적으로 하드웨어에 구현될 수 있는 모델을 고안한다.현재까지 P계통은 실용계통이 주어지기는 하지만 실천으로 축소된 적이 없는 거의 모든 이론적 모델이다.^[2]null

참고 항목

• 생물학적 시스템 모델링

참조