미쉘 구조

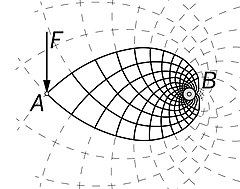
Michell 구조는 A.G.M. Michell이 1904년 ^[1]자주 언급한 논문에서 정의한 기준에 따라 최적의 구조입니다.

Michell은 "프레임(현재는 트러스라고 불린다)은 동일한 힘을 가한 프레임 구조에서 가능한 재료의 경제성의 한계에 도달한다. 프레임이 차지하는 공간이 적절한 작은 변형에 의해 프레임의 모든 바의 변형률이 동일한 길이의 부분만큼 증가할 수 있다면, 공간의 어떤 요소의 길이 부분적 변화보다 작으면 안 된다."

위의 결론은 Maxwell 로드 패스 정리에 기초하고 있습니다.

$\displaystyle \sum _{}l_{p}f_{p}-\sum _{}l_{q}f_{q}=C}$

Where $f_{p}$ is the tension value in any tension element of length $l_{p}$ , $f_{q}$ is the compression value in any compression element of length $l_{q}$ and $C$ is a constant value which is based on exter구조물에 적용되는 nal 하중

Maxwell 로드 패스 정리에 따라 텐션 부재 \ $\textstyle \sum _{}l_{p}f_{p}$ l $\textstyle \sum _{}l_{p}f_{p}$ \ $displaystyle$ \ $textstyle \sum$ _ { $p }$ f _ { p $\textstyle \sum _{}l_{p}f_{p}$ } f _ { p } f _ { p } f _ { p $}$ f _ { p $\textstyle \sum _{}l_{p}f_{p}$ }} 의 부하 패스를 감소시키면 외부 부하 세트에서의 압축 요소 $\textstyle \sum _{}l_{q}f_{q}$ $\textstyle \sum _{}l_{q}f_{q}$ $\textstyle \sum _{}l_{q}f_{q}$ $\textstyle \sum _{}l_{q}f_{q}$ q f q \ $displaystyle$ \ $textstyle$ \ sum $\sum$ \sum \sum \ $sum$ \sum _ { { { { } f _ { { } f } 의 $부하$ 패스와 같은 값만큼 감소합니다.최소 부하 경로를 가진 구조물은 최소한의 컴플라이언스를 갖는 구조이다(이러한 하중의 값에 의해 가중치가 가해지는 하중의 포인트에서 최소 가중치 편향을 갖는 구조).따라서 미쉘 구조는 최소한의 컴플라이언스 트러스입니다.

특수한 경우

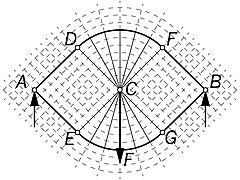
(가) 트러스의 모든 막대는 동일한 부호(장력 또는 압축)의 하중을 받는다.

재료의 필요한 부피는 주어진 하중 세트에 대해 가능한 모든 경우에 동일하다.Michell은 필요한 재료의 최소 부피를 다음과 ${\textstyle V_{m}={\frac {\sum _{}lf}{P}}}$ 정의합니다. ${\textstyle V_{m}={\frac {\sum _{}lf}{P}}}$ m ${\textstyle V_{m}={\frac {\sum _{}lf}{P}}}$ ${\textstyle V_{m}={\frac {\sum _{}lf}{P}}}$ F ${\textstyle V_{m}={\frac {\sum _{}lf}{P}}}$ { $textstyle$ V _ { m } = $fr$ frac { $sum$ _ { { } $lf }$

$P$ 서 P $(\displaystyle$ P $)$ 는 $P$ 재료의 허용 응력입니다.

(이) 장력봉과 압축봉의 혼재

보다 일반적인 경우는 적절한 변형 전후에 직교계의 곡선을 형성하는 막대로 구성된 프레임이다.2차원 직교 시스템은 동일한 계열의 인접한 두 곡선 사이의 기울기가 길이 전체에 걸쳐 일정할 경우에만 하나의 곡선을 늘어뜨리고 동일한 변형률로 다른 것을 압축한 후에도 직교 상태를 유지한다.이 요건은 일련의 수직 곡선이 다음 중 하나가 되도록 합니다.

a) 접선 및 인볼루트 시스템 또는

b) 교차하는 로그 나선계.

직선 또는 원은 로그 완화곡선의 특수한 경우입니다.

예

Michell은 최적의 프레임의 몇 가지 예를 제시했습니다.

a	b	c	d	e

A에 가해지고 선 AB에 직각으로 작용하는 단일 힘 F	A와 B 지점의 지지대 사이에 중심을 맞춘 C에 가해지는 단일 힘 F(전체 공간 솔루션)	A와 B 지점의 지지대 사이에 중심을 맞춘 C에 가해지는 단일 힘 F(반공간 용액)	지지대 사이의 직선으로부터 힘이 떨어진 중앙 부하 빔.사례 b 및 c와 유사한 구조	직선 AB의 점 A, B에 등가 및 역가 커플이 적용됩니다.최소 프레임은 A와 B에 극이 있는 구의 경사에 대해 45도로 기울어진 일련의 마름모꼴 선으로 구성된다.

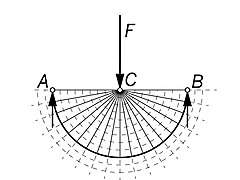
프라거 트러스

최근 몇 년 동안 이산 최적 ^[2]^[3]^[4]트러스에서 많은 연구가 수행되었습니다.미첼 트러스는 연속체(부재의 무한수)에 대해 정의되지만, 미첼 트러스로도 불리기도 합니다.이산 최적 트러스(일반적으로 캔틸레버)의 최적 위상을 얻기 위해 상대 변위 원의 방법을 사용한 William Prager는 이산 최적 트러스 주제에 상당한 기여를 했다.Prager의 공헌을 인식하기 위해 분리된 Michell 트러스를 Prager 트러스라고 부르기도 합니다.이후 캔틸레버 프라거 트러스의 기하학적 형상은 3점 또는 3개의 힘 문제에 대해 최적의 이산 트러스 부재 간의 특정한 기하학적 관계를 발견한 마주렉, 베이커 및 토트에 의해 공식화되었습니다.

레퍼런스

^ 미첼, A. G. M. (1904)골격 구조에서 재료의 경제적 한계, 철학 잡지, 제8권(47), 페이지 589-597.
^ Prager W., 응용 기계 및 엔지니어링의 이산화된 미쉘 구조, 컴퓨터 방법에 관한 메모, 제3권, 349-355페이지, 1974년
^ Prager W. 캔틸레버 트러스 최적 배치, 최적화 이론 및 응용 저널(1989) 23: 111. https://doi.org/10.1007/BF00932301
^ Prager W. 트러스, 컴퓨터 및 구조물의 거의 최적의 설계 ISSN0045-7949, Vol: 8, 발행: 3, 페이지: 451-454, 1978
^ Mazurek, A., Baker W.F. & Tort, C., 구조와 같은 최적의 트러스의 기하학적 측면, 구조 및 다원적 최적화(2011) 43: 231.https://doi.org/10.1007/s00158-010-0559-x
^ Mazurek, A. 3가지 힘 문제를 위한 구조와 같은 최적의 트러스 기하학적 측면, 구조 및 다원적 최적화(2012) 45: 21. https://doi.org/10.1007/s00158-011-0679-y

[1] 미첼, A. G. M. (1904)골격 구조에서 재료의 경제적 한계, 철학 잡지, 제8권(47), 페이지 589-597.

[2] Prager W., 응용 기계 및 엔지니어링의 이산화된 미쉘 구조, 컴퓨터 방법에 관한 메모, 제3권, 349-355페이지, 1974년

[3] Prager W. 캔틸레버 트러스 최적 배치, 최적화 이론 및 응용 저널(1989) 23: 111. https://doi.org/10.1007/BF00932301

[4] Prager W. 트러스, 컴퓨터 및 구조물의 거의 최적의 설계 ISSN0045-7949, Vol: 8, 발행: 3, 페이지: 451-454, 1978

[5] Mazurek, A., Baker W.F. & Tort, C., 구조와 같은 최적의 트러스의 기하학적 측면, 구조 및 다원적 최적화(2011) 43: 231.https://doi.org/10.1007/s00158-010-0559-x

[6] Mazurek, A. 3가지 힘 문제를 위한 구조와 같은 최적의 트러스 기하학적 측면, 구조 및 다원적 최적화(2012) 45: 21. https://doi.org/10.1007/s00158-011-0679-y

[1]

[2]

[3]

[4]

Search

미쉘 구조

네임스페이스

더

목차

특수한 경우

예

프라거 트러스

레퍼런스