미 퍼텐셜

Mie 퍼텐셜은 원자 수준에서 입자들 사이의 상호작용을 설명하는 상호작용 퍼텐셜입니다. 대부분 분자 간 상호 작용을 설명하는 데 사용되지만 때로는 분자 간 상호 작용, 즉 결합을 모델링하는 데도 사용됩니다.

미에 퍼텐셜은 독일의 물리학자 구스타프 미에의^[1] 이름을 따서 지어졌지만 분자간 퍼텐셜의 역사는 더 복잡합니다^[2][3][4]. 미에 포텐셜은 LJ(Lennard-Jones) 포텐셜의 일반화된 경우로, 아마도 가장 널리 사용되는 쌍 포텐셜일 것입니다.^[5][6]

Mie 퍼텐셜 $)$ {\$displaystyle$ V$(r)}$는 두 입자 사이의$$$거리$인$$r {\$displayr}$의 함수이며 다음과^[7] 같이 기록됩니다.

${\displaystyle V(r)=C\,\varepsilon \left[\left ({\frac {\sigma }{r}}\right)^{n}-\left ({\frac {\sigma }{r}}\right)^{m}\right],~~~(1)}$

와 함께

${\displaystyle C}$ = ${\displaystyle n}$ $n$- m (n m ) m n - m {\displaystyl${\displaystyle e}$ C = {\frac {n}{n-m}}\l${\displaystyle \mathrm{ef}}$t ({\frac {n}{m}\right)^{\frac {m}{n-m}}.

Lennard-Jones 전위는 식 (1)에서 $n$= $12 {\$textstyle n = 12$}$이고 m = 6 {\textstyle m = 6}인 특수한 경우에 해당합니다. 식 (1)에서$$ε ${\$displaystyle \varepsilon }는 분산 $에너지$이고$,$ σ${\displaystyle$ \sigma }는 V = 0 ${\displaystyle$ V = 0$}$이 되는 거리를 나타내며, 이를 "collision 반경"이라고도 합니다. 파라미터$$σ {\textstyle$$\sigma}는 일반적으로 충돌에 관련된 입자의 크기를 나타냅니다. $매개$ 변수 $n$ ${\textstyle n}$ 및 m$$ ${\textstyle$ m$}$은 전위의 모양을$$ 특징으로 합니다. $n$ ${\textstyle$ n$}$은 반발의 문자를 설명하고$$ $m$ ${\textstyle$ m$}$은 $끌림$의 문자를 설명합니다$$.

매력적인 지수 m = $6$ $\{\backslash \mathrm{textstyle}$ m = 6}은 런던 분산력에 의해 물리적으로 정당화되지만 반발 지수에 대한 특정 값에 대한 정당성은 알려져 있지 않습니다. 반발 첨도 매개변수 $n$ ${\textstyle n}$은 압축성 및 음속과 같은 열역학적 유도 특성의 모델링에 상당한 영향을 미칩니다$$. 따라서 Mie 전위는 단순한 Lennard-Jones 전위보다 더 유연한 분자간 전위입니다.

Mie 전위는 오늘날 분자 모델링의 많은 힘 분야에서 사용됩니다. 일반적으로 매력 지수는 $m$ = ${\$textstyle m = 6}으로 선택되고 반발 지수는 모델 피팅 동안 조정 가능한 매개 변수로 사용됩니다.

미에 물질의 열물리적 특성

레나드-존스 퍼텐셜에 의해 상호작용하는 입자에 의해 정의되는 이론적 물질이 존재하는 레나드-존스움의 경우, 주어진 미에 퍼텐셜에 의해 상호작용하는 입자로 정의되는 미에 물질의 물질 클래스가 존재합니다. 실질적으로 무한히 많은 미에 퍼텐셜이 존재하기 때문에 (다른 n, m 매개변수를 사용하여) 동일하게 많은 미에 물질이 존재합니다. - 이것은 고유하게 정의된 Lennard-Jonesium과 반대입니다.

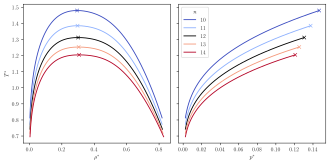
Mie 물질의 열 물리적 특성은 최근 몇 년 동안 바이러스 계수와^[8] 계면^[9] 및^{[10][11][12][13]} 증기-액 평형 특성을 포함한 수많은 논문의 주제가 되었습니다. 이와 같은 연구를 바탕으로 상호작용 포텐셜의 모양(n과 m으로 설명) 사이의 관계가 밝혀졌습니다.

또한 상태 모델의 여러 열역학 방정식과 수송 특성 모델과 같은 Mie 물질의 열 물리적 특성을 설명하기 위한 많은 이론적(해석적) 모델이 개발되었습니다.

서로 다른 많은 조합(${\displaystyle n,}$ m ${\displaystyle n,$ m$\})$이 유사한 위상 동작을^[18] 산출할 수 있는 것으로 관찰되었습니다. 이 문제에 대한 해결책으로 파라미터가 발견되었습니다.

${\displaystyle \alpha = C\left[{\frac {1}{m-3}}-{\frac {1}{n-3}}\right]}$

Mie 유체를 설명하는 데 사용할 수 있으며 $지수$는 다르지만 동일한 α {\displaystyle $\alpha }$ - 매개$$ 변수는 동일한 $위상{\displaystyle }$ 동작을 나타냅니다$.$^[18]

일부 물질에 대한 잠재적 매개변수

유연성 때문에 미에 전위는 실제 유체를 모델링하는 데 인기 있는 선택입니다. 아래 표에는 증기-액체 평형, 표면 장력, 기화 엔탈피 또는 기타 열역학적 특성과 같은 다양한 유체 특성으로 회귀된 문헌의 파라미터가 나와 있습니다. Well-depth 파라미터$($ε ${\$displaystyle$$\varepsilon })는 일반적으로${\displaystyle }$ε ∗ =$$ε$$/ kB {\displaystyle \varepsilon ^{*}=\varepsilon / k_{B}}로${\displaystyle {}^{}}보고$되며, 여기서 kB {\displaystyle k_{B}}는 볼츠만 상수입니다.

종	$σ${\$displaystyle \$sigma} [Å]	$ε {\$displaystyle \varepsilon} [k B - 1 {\displaystyle k_{B}^{-1}}	$n {\displaystyle$ n$}$ $$[ – ]	$m {\displaystyle$ m$}$ $$[ – ]	심판.
${\displaystyle {\ce {Ar}}}$	3.404	117.84	12.085	6.0	[19]
${\displaystyle {\ce {CH_4}}$	3.7412	153.36	12.65	6.0	[20]
${\displaystyle {\ce {H_2}}$	3.2574	17.931	8.0	6.0	[21]
${\displaystyle {\ce {He}}}$	3.3530	4.44	14.84	6.0	[21]
${\displaystyle {\ce {Kr}}}$	3.645	176.10	14.0	6.0	[22]
${\displaystyle {\ce {N_2}}$	3.609	105.79	14.08	6.0	[23]
${\displaystyle {\ce {O_2}}$	3.46	118.0	12.0	6.0	[24]

참고문헌