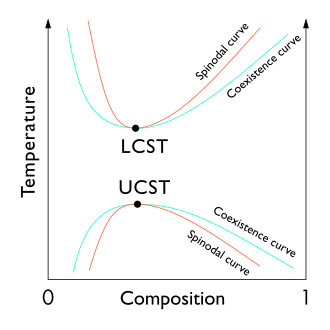임계점(열역학)

아임계 에탄, 액체 및 기체상이 공존합니다.
임계점(32.17°C, 48.72bar), 오팔렌스.
초임계 에탄,^[1] 유체

열역학에서 임계점(또는 임계 상태)은 위상 평형 곡선의 끝점입니다.가장 두드러진 예는 액체와 그 증기가 공존할 수 있는 조건을 나타내는 압력-온도 곡선의 끝점인 액체-증기 임계점이다.고온에서는 압력만으로는 가스를 액화할 수 없습니다.임계 온도_c T와 임계 압력_c p로 정의되는 임계점에서는 위상 경계가 사라진다.다른 예로는 혼합물의 액체-액체 임계점과 외부 자기장이 ^[2]없는 경우의 강자석-파라매그넷 전이 등이 있다.

액체-증기 임계점

개요

압력-온도 상 다이어그램에서 액체-증기 임계점은 액체-기체 상 경계의 고온 극단에 있습니다.녹색 점선은 물의 비정상적인 동작을 나타냅니다.

단순성과 명확성을 위해 임계점에 대한 일반적인 개념은 특정 예인 기액 임계점에 대해 논의함으로써 가장 잘 소개된다.이것은 발견된 첫 번째 임계점이었고, 여전히 가장 잘 알려져 있고 가장 많이 연구되고 있는 지점이다.

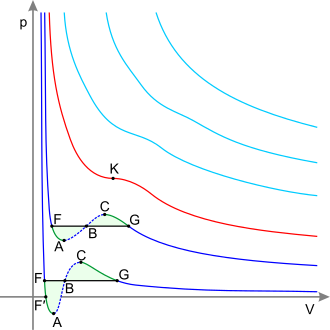
오른쪽 그림은 (아래에서 논의된 추가 상태 변수와 풍부한 위상도를 가진 혼합물이 아닌) 순수 물질의 도식 PT 도표를 보여줍니다.일반적으로 알려진 상은 위상 경계, 즉 압력-온도 조합에 의해 분리되며, 두 상은 공존할 수 있다.트리플 포인트에서는, 3개의 위상이 모두 공존할 수 있습니다.단, 액체-증기 경계는 임계 온도_c T와 임계 압력_c p에서 끝점으로 끝납니다.이것이 중요한 포인트입니다.

물에서 임계점은 647.096K(373.946°C; 705.103°F)와 22.064메가파스칼(3,200.1psi; 217.75atm)^[3]에서 발생한다.

임계점 부근에서는 액체와 증기의 물리적 특성이 극적으로 변화하며 두 상은 더욱 유사해집니다.예를 들어, 정상 조건에서의 액체 물은 거의 압축할 수 없고 열팽창 계수가 낮고 유전율이 높으며 전해질에 뛰어난 용매이다.임계점 근처에서는 이러한 모든 특성이 정반대로 바뀝니다. 즉, 물은 압축성, 팽창성, 유전체 불량, 전해질 불량 용매이며, 비극성 가스 및 유기 ^[4]분자와 혼합하는 것을 선호합니다.

임계점에서는 한 단계만 존재합니다.기화열은 0입니다.PV 다이어그램의 항온선(임계 등온선)에는 정지 변곡점이 있습니다.즉,^[5]^[6]^[7] 임계점에서는 다음과 같습니다.

\displaystyle \left({\frac\partial p}{\partial V}}\right)_{T}=0,}

\displaystyle \left({\frac {partial ^{2}p}{\partial V^{2}}\right)_{T}=0.}

가스의 등온도입니다.빨간색 선은 임계 등온선이며 임계점은 K입니다.파선은 등온선의 일부를 나타내며, 구배가 양수이므로 금지되어 이 영역의 가스가 음의 압축성을 갖게 됩니다.

임계점 위에는 액체 및 기체 상태와 연속적으로 연결된 물질 상태가 있습니다(상전이 없이 변환될 수 있음).그것은 초임계 유체라고 불립니다.액체와 증기의 모든 구별이 임계점을 넘어 사라진다는 일반적인 교과서 지식은 피셔와 ^[8]위돔이 도전했다. 피셔는 서로 다른 점근 통계 특성을 가진 상태를 분리하는 p-T 선을 식별했다(피셔-위돔 선).

임계점은^[ambiguous] 대부분의 열역학적 또는 기계적 특성에서 나타나지 않고 "숨겨져" 탄성 모듈리의 불균일성 시작, 비아핀 물방울의 외관 및 국소적 특성에서의 현저한 변화, 결함 쌍 ^[9]집중도의 갑작스러운 향상으로 나타난다.

역사

초임계 온도에서 임계 온도로 냉각하는 동안 임계 이산화탄소가 안개를 내뿜습니다.

임계점의 존재는 1822년^[10]^[11] Charles Cagniard de la Tour에 의해 처음 발견되었고 1860년^[12]^[13] Dmitri Mendelev와 ^[14]1869년 Thomas Andrews에 의해 명명되었다.Cagniard는 CO가 73atm의 압력에서 31°C에서 액화될 수 있지만 3000atm의 압력에서도 약간 높은 온도에서는 액화되지 않는다는 것을₂ 보여주었다.

이론.

위의 조건 $(\partial p/\partial V)_{T}=0$ p / $v$ V )의 해결 T $(\partial p/\partial V)_{T}=0$ \ $displaystyle (\ displaystyle$ ) $_$ {T $}=0$ 판데르발스 방정식의 임계점은 다음과 같이 계산할 수 있다.

({displaystyle T_{\text{c}}=squalfrac {8a}{27Rb}},\quad V_{\text{c}=3nb,\quad p_{\text{c}=squalfrac {a}{27b^{2}}).}

그러나 평균장 이론에 기초한 판 데르 발스 방정식은 임계점 근처에서는 유지되지 않는다.특히 잘못된 스케일링 법칙을 예측합니다.

임계점 부근의 유체의 특성을 분석하기 위해 임계 특성과^[15] 관련하여 감소 상태 변수를 정의하기도 한다.

T_{\text{r}}=black {T}{T_{\text{c}}},\quad p_{\text{r}}=sqfrac {p}{p_{\text{c}}}},\sq V_{\text{r}}=sqfrac {V}{}}}},\squad p_{\text{r}}}},RT_{\text{c}}/p_{\text{c}}}}.

해당 상태의 원리는 동일한 감소 압력과 온도에서 물질이 동일한 감소 부피를 갖는다는 것을 나타냅니다.이 관계는 많은 물질에 대해 거의 사실이지만 p 값이_r 클수록 부정확해집니다.

일부 기체의 경우, 뉴턴 보정이라고 불리는 추가적인 보정 계수가 이러한 방식으로 계산된 임계 온도와 임계 압력에 추가됩니다.이 값은 경험적으로 도출된 값이며 관심 ^[16]압력 범위에 따라 달라집니다.

선택된 물질의 액체-증기 임계 온도 및 압력 표

물질^[17]^[18]	임계 온도	임계 압력(절대)
아르곤	-122.4°C(150.8K)	48.1 atm (4,870 kPa)
암모니아(NH₃)^[19]	132.4 °C (405.5 K)	111.3 ATM (11,280 kPa)
R-134a	101.06°C(374.21K)	40.06 ATM (4,059 kPa)
R-410A	72.8 °C (345.9 K)	47.08 atm (4,770 kPa)
브롬	310.8°C(584.0K)	102 ATM (10,300 kPa)
세슘	1,664.85°C (1,938.00K)	94 ATM (9,500 kPa)
염소	143.8°C(416.9K)	76.0 atm (7,700 kPa)
에탄(CH₂₆)	31.17 °C (304.32 K)	48.077 atm (4,871.4 kPa)
에탄올(CHOH₂₅)	241 °C (514 K)	62.18 atm (6,300 kPa)
불소	-128.85°C(144.30K)	51.5 ATM (5,220 kPa)
헬륨	−267.96 °C (5.19 K)	2.24 ATM (227 kPa)
수소	-239.95°C(33.20K)	12.8 atm (1,300 kPa)
크립톤	- 63.8 °C (209.3 K)	54.3 ATM (5,500 kPa)
메탄(CH₄)	-82.3°C(190.8K)	45.79 atm (4,640 kPa)
네온	-228.75°C(44.40K)	27.2 ATM (2,760 kPa)
질소	-146.9°C(126.2K)	33.5 atm (3,390 kPa)
산소(O₂)	-118.6°C(154.6K)	49.8 atm (5,050 kPa)
이산화탄소(CO₂)	31.04 °C (304.19 K)	72.8 atm (7,380 kPa)
아산화질소(NO₂)	36.4 °C (309.5 K)	71.5 ATM (7,240 kPa)
황산(HSO₂₄)	654 °C (927 K)	45.4 ATM (4,600 kPa)
제논	16.6 °C (289.8 K)	57.6 ATM (5,840 kPa)
리튬	2,950 °C (3,220 K)	652 ATM (66,100 kPa)
수성.	1,476.9°C(1,750.1K)	1,720 ATM(174,000kPa)
유황	1,040.85°C(1,314.00K)	207 ATM (21,000 kPa)
철	8,227 °C (8,500 K)
골드	6,977 °C (7,250 K)	5,000 ATM (510,000 kPa)
알루미늄	7,577 °C (7,850 K)
물(HO₂)^[3]^[20]	373.946°C(647.096K)	217.7 ATM (22,060 kPa)

혼합물: 액체-액체 임계점

LCST와 UCST의 두 가지 임계점을 포함한 전형적인 고분자 용액의 위상 거동 그림

임계용액 온도에서 발생하는 용액의 액체 임계점은 위상도의 2상 영역의 한계에서 발생한다.다시 말해, 오른쪽의 중합체-용제 위상 다이어그램에서 보듯이, 온도 또는 압력과 같은 일부 열역학 변수의 미세한 변화가 혼합물을 두 개의 뚜렷한 액체상으로 분리하는 지점입니다.두 가지 유형의 액체 임계점은 냉각이 상 분리를 유도하는 가장 뜨거운 지점인 UCST(Unpper Critical Solution Temperature)와 가열이 상 분리를 유도하는 가장 차가운 지점인 LCST(Lower Critical Solution Temperature)입니다.

수학적 정의

이론적인 관점에서 액체 임계점은 스피노달 곡선의 온도 농도 극단을 나타낸다(오른쪽 그림 참조).따라서, 2성분 시스템의 액체-액체 임계점은 두 가지 조건을 만족해야 한다: 스피노달 곡선의 조건(농도에 대한 자유 에너지의 두 번째 도함수)과 극한 조건(농도에 대한 자유 에너지의 세 번째 도함수)은 0 또는 der와 같아야 한다.스피노달 온도의 농도 대비 스피노달 온도 Ivivative.

「」를 참조해 주세요.

등각장론
임계 지수
임계 현상(고급 기사)
요소의 임계점(데이터 페이지)
퀴리점
Joback법, Klincewicz법, Lydersen법(분자구조에서 임계온도, 압력, 부피 추정)
액체 임계점
중요 솔루션의 온도를 낮추다
네엘점
침투 임계값
상전이
러시브룩 부등식
척도 불변성
자기 조직화된 중요도
초임계 유체, 초임계 건조, 초임계 물 산화, 초임계 유체 추출
삼각점
트리플 포인트
임계 솔루션 온도 상한
Widom 스케일링

각주

^ Horstmann, Sven (2000). Theoretische und experimentelle Untersuchungen zum Hochdruckphasengleichgewichtsverhalten fluider Stoffgemische für die Erweiterung der PSRK-Gruppenbeitragszustandsgleichung [Theoretical and experimental investigations of the high-pressure phase equilibrium behavior of fluid mixtures for the expansion of the PSRK group contribution equation of state] (Ph.D.) (in German). Oldenburg, Germany: Carl-von-Ossietzky Universität Oldenburg. ISBN 3-8265-7829-5. OCLC 76176158.
^ Stanley, H. Eugene (1987). Introduction to phase transitions and critical phenomena. New York: Oxford University Press. ISBN 0-19-505316-8. OCLC 15696711.
^ ^a ^b Wagner, W.; Pruß, A. (June 2002). "The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use". Journal of Physical and Chemical Reference Data. 31 (2): 398. doi:10.1063/1.1461829.
^ Anisimov, Sengers, Levelt Sengers (2004) :수계통의 거의 치명적인 동작.상승된 온도 및 압력에서의 수계 제2장 Palmer 등, ed.엘세비어
^ P. Atkins and J. de Paula, 물리화학, 제8판 (W. H. Freeman 2006), 페이지 21.
^ K. J. Laidler와 J. H. Meiser, 물리화학 (Benjamin/Cummings 1982), 페이지 27.
^ P. A. Rock, 화학 열역학 (MacMillan 1969), 페이지 123.
^ Fisher, Widom: 선형 시스템의 상관 관계 붕괴, J. Chem.Phys. 50, 3756(1969년)
^ Das, Tamoghna; Ganguly, Saswati; Sengupta, Surajit; Rao, Madan (3 June 2015). "Pre-Yield Non-Affine Fluctuations and A Hidden Critical Point in Strained Crystals". Scientific Reports. 5 (1): 10644. Bibcode:2015NatSR...510644D. doi:10.1038/srep10644. PMC 4454149. PMID 26039380.
^ Charles Cagniard de la Tour (1822). "Exposé de quelques résultats obtenu par l'action combinée de la chaleur et de la compression sur certains liquides, tels que l'eau, l'alcool, l'éther sulfurique et l'essence de pétrole rectifiée" [Presentation of some results obtained by the combined action of heat and compression on certain liquids, such as water, alcohol, sulfuric ether (i.e., diethyl ether), and distilled petroleum spirit]. Annales de Chimie et de Physique (in French). 21: 127–132.
^ Berche, B., Henkel, M., Kenna, R(2009) 임계 현상: Cagniard de la Tour 이후 150년.물리학 저널 13(3), 3001-1–3001-4페이지.
^
멘델레예프는 임계점을 "절대 끓는 온도"라고 불렀다.
- Менделеев, Д. (1861). "О расширении жидкостей от нагревания выше температуры кипения" [On the expansion of liquids from heating above the temperature of boiling]. Горный Журнал [Mining Journal] (in Russian). 4: 141–152. "비등 절대 온도"는 페이지 151에 정의되어 있습니다.Wikimedia에서 이용 가능
- 독일어 번역:Mendelejeff, D(1861년)."Ueber Ausdehnung 데르 Flüssigkeiten beim Erwärmen über ihren Siedepunkt 죽"[유체의 그들의 비등점 이상 가열 동안 확장에].Annalen하는 Chemie Pharmacie(독일어로)und.119:1–11. doi:10.1002/jlac.18611190102.그" 끓는 절대 온도"페이지의 주 11:``에어로빅(로서"Als 절대 Siedetemperatur müssen wir den Punkt betrachten,beiwelchem 1) 죽Cohäsion 데르 Flüssigkeit=0°ist 운트 a2=0으로,bei welcher 2) 죽latente Verdamfungswärme auch)0ist 운트 bei 의무 불이행자 sich 3) 죽Flüssigkeit Dampf verwandelt에,unabhängig 폰 Druck 운트 Volum."에 정의되어 있다.끓는 용질 온도"는 (1) 액체의 응집력이 0°이고² a = 0인 점을 고려해야 한다. [여기서² a는 모세관 계수, 페이지 6], (2) 기화의 잠열도 0이며 (3) 액체가 압력과 부피와 무관하게 증기로 변환된다.)
- 1870년에, 멘델레 예프, 토머스 앤드루스, 가장 중요한 시점의 정의에 관한 그의 우선 순위에 대해:주장했다.Mendelejeff, D(1870년)."Bemerkungen zu den Untersuchungen 폰 앤드루스 über 다이 Compressibilität 데르 Kohlensäure"[그 압축성으로 이산화 탄소의 앤드류스의 조사를 평].Annalender Physik.2시리즈(독일어로).141(12):618–626.Bibcode:1870AnP...217..618M. doi:10.1002/andp.18702171218.
^ 란다우, 리프시츠, 이론물리학, Vol.통계물리학, 제83장 [독일판 1984]
^ Andrews, Thomas (1869). "The Bakerian lecture: On the continuity of the gaseous and liquid states of matter". Philosophical Transactions of the Royal Society. London. 159: 575–590. doi:10.1098/rstl.1869.0021. 588페이지에 "임계점"이라는 용어가 표시됩니다.
^ Cengel, Yunus A.; Boles, Michael A. (2002). Thermodynamics: an engineering approach. Boston: McGraw-Hill. pp. 91–93. ISBN 978-0-07-121688-3.
^ Maslan, Frank D.; Littman, Theodore M. (1953). "Compressibility Chart for Hydrogen and Inert Gases". Ind. Eng. Chem. 45 (7): 1566–1568. doi:10.1021/ie50523a054.
^ Emsley, John (1991). The Elements (Second ed.). Oxford University Press. ISBN 978-0-19-855818-7.
^ Cengel, Yunus A.; Boles, Michael A. (2002). Thermodynamics: An Engineering Approach (Fourth ed.). McGraw-Hill. pp. 824. ISBN 978-0-07-238332-4.
^ "Ammonia - NH3 - Thermodynamic Properties". www.engineeringtoolbox.com. Retrieved 2017-04-07.
^ "Critical Temperature and Pressure". Purdue University. Retrieved 2006-12-19.

레퍼런스

"Revised Release on the IAPWS Industrial Formulation 1997 for the Thermodynamic Properties of Water and Steam" (PDF). International Association for the Properties of Water and Steam. August 2007. Retrieved 2009-06-09.

외부 링크

"Critical points for some common solvents". ProSciTech. Archived from the original on 2008-01-31.
"Critical Temperature and Pressure". Department of Chemistry. Purdue University. Retrieved 2006-12-03.

[1] Horstmann, Sven (2000). Theoretische und experimentelle Untersuchungen zum Hochdruckphasengleichgewichtsverhalten fluider Stoffgemische für die Erweiterung der PSRK-Gruppenbeitragszustandsgleichung [Theoretical and experimental investigations of the high-pressure phase equilibrium behavior of fluid mixtures for the expansion of the PSRK group contribution equation of state] (Ph.D.) (in German). Oldenburg, Germany: Carl-von-Ossietzky Universität Oldenburg. ISBN 3-8265-7829-5. OCLC 76176158.

[2] Stanley, H. Eugene (1987). Introduction to phase transitions and critical phenomena. New York: Oxford University Press. ISBN 0-19-505316-8. OCLC 15696711.

[IAPWS95-3] Wagner, W.; Pruß, A. (June 2002). "The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use". Journal of Physical and Chemical Reference Data. 31 (2): 398. doi:10.1063/1.1461829.

[4] Anisimov, Sengers, Levelt Sengers (2004) :수계통의 거의 치명적인 동작.상승된 온도 및 압력에서의 수계 제2장 Palmer 등, ed.엘세비어

[Atkins-5] P. Atkins and J. de Paula, 물리화학, 제8판 (W. H. Freeman 2006), 페이지 21.

[6] K. J. Laidler와 J. H. Meiser, 물리화학 (Benjamin/Cummings 1982), 페이지 27.

[7] P. A. Rock, 화학 열역학 (MacMillan 1969), 페이지 123.

[8] Fisher, Widom: 선형 시스템의 상관 관계 붕괴, J. Chem.Phys. 50, 3756(1969년)

[9] Das, Tamoghna; Ganguly, Saswati; Sengupta, Surajit; Rao, Madan (3 June 2015). "Pre-Yield Non-Affine Fluctuations and A Hidden Critical Point in Strained Crystals". Scientific Reports. 5 (1): 10644. Bibcode:2015NatSR...510644D. doi:10.1038/srep10644. PMC 4454149. PMID 26039380.

[10] Charles Cagniard de la Tour (1822). "Exposé de quelques résultats obtenu par l'action combinée de la chaleur et de la compression sur certains liquides, tels que l'eau, l'alcool, l'éther sulfurique et l'essence de pétrole rectifiée" [Presentation of some results obtained by the combined action of heat and compression on certain liquids, such as water, alcohol, sulfuric ether (i.e., diethyl ether), and distilled petroleum spirit]. Annales de Chimie et de Physique (in French). 21: 127–132.

[11] Berche, B., Henkel, M., Kenna, R(2009) 임계 현상: Cagniard de la Tour 이후 150년.물리학 저널 13(3), 3001-1–3001-4페이지.

[12] 멘델레예프는 임계점을 "절대 끓는 온도"라고 불렀다.
Менделеев, Д. (1861). "О расширении жидкостей от нагревания выше температуры кипения" [On the expansion of liquids from heating above the temperature of boiling]. Горный Журнал [Mining Journal] (in Russian). 4: 141–152. "비등 절대 온도"는 페이지 151에 정의되어 있습니다.Wikimedia에서 이용 가능

독일어 번역:Mendelejeff, D(1861년)."Ueber Ausdehnung 데르 Flüssigkeiten beim Erwärmen über ihren Siedepunkt 죽"[유체의 그들의 비등점 이상 가열 동안 확장에].Annalen하는 Chemie Pharmacie(독일어로)und.119:1–11. doi:10.1002/jlac.18611190102.그" 끓는 절대 온도"페이지의 주 11:``에어로빅(로서"Als 절대 Siedetemperatur müssen wir den Punkt betrachten,beiwelchem 1) 죽Cohäsion 데르 Flüssigkeit=0°ist 운트 a2=0으로,bei welcher 2) 죽latente Verdamfungswärme auch)0ist 운트 bei 의무 불이행자 sich 3) 죽Flüssigkeit Dampf verwandelt에,unabhängig 폰 Druck 운트 Volum."에 정의되어 있다.끓는 용질 온도"는 (1) 액체의 응집력이 0°이고² a = 0인 점을 고려해야 한다. [여기서² a는 모세관 계수, 페이지 6], (2) 기화의 잠열도 0이며 (3) 액체가 압력과 부피와 무관하게 증기로 변환된다.)

1870년에, 멘델레 예프, 토머스 앤드루스, 가장 중요한 시점의 정의에 관한 그의 우선 순위에 대해:주장했다.Mendelejeff, D(1870년)."Bemerkungen zu den Untersuchungen 폰 앤드루스 über 다이 Compressibilität 데르 Kohlensäure"[그 압축성으로 이산화 탄소의 앤드류스의 조사를 평].Annalender Physik.2시리즈(독일어로).141(12):618–626.Bibcode:1870AnP...217..618M. doi:10.1002/andp.18702171218.

[13] Менделеев, Д. (1861). "О расширении жидкостей от нагревания выше температуры кипения" [On the expansion of liquids from heating above the temperature of boiling]. Горный Журнал [Mining Journal] (in Russian). 4: 141–152. "비등 절대 온도"는 페이지 151에 정의되어 있습니다.Wikimedia에서 이용 가능

[14] 독일어 번역:Mendelejeff, D(1861년)."Ueber Ausdehnung 데르 Flüssigkeiten beim Erwärmen über ihren Siedepunkt 죽"[유체의 그들의 비등점 이상 가열 동안 확장에].Annalen하는 Chemie Pharmacie(독일어로)und.119:1–11. doi:10.1002/jlac.18611190102.그" 끓는 절대 온도"페이지의 주 11:``에어로빅(로서"Als 절대 Siedetemperatur müssen wir den Punkt betrachten,beiwelchem 1) 죽Cohäsion 데르 Flüssigkeit=0°ist 운트 a2=0으로,bei welcher 2) 죽latente Verdamfungswärme auch)0ist 운트 bei 의무 불이행자 sich 3) 죽Flüssigkeit Dampf verwandelt에,unabhängig 폰 Druck 운트 Volum."에 정의되어 있다.끓는 용질 온도"는 (1) 액체의 응집력이 0°이고² a = 0인 점을 고려해야 한다. [여기서² a는 모세관 계수, 페이지 6], (2) 기화의 잠열도 0이며 (3) 액체가 압력과 부피와 무관하게 증기로 변환된다.)

[15] 1870년에, 멘델레 예프, 토머스 앤드루스, 가장 중요한 시점의 정의에 관한 그의 우선 순위에 대해:주장했다.Mendelejeff, D(1870년)."Bemerkungen zu den Untersuchungen 폰 앤드루스 über 다이 Compressibilität 데르 Kohlensäure"[그 압축성으로 이산화 탄소의 앤드류스의 조사를 평].Annalender Physik.2시리즈(독일어로).141(12):618–626.Bibcode:1870AnP...217..618M. doi:10.1002/andp.18702171218.

[13] 란다우, 리프시츠, 이론물리학, Vol.통계물리학, 제83장 [독일판 1984]

[14] Andrews, Thomas (1869). "The Bakerian lecture: On the continuity of the gaseous and liquid states of matter". Philosophical Transactions of the Royal Society. London. 159: 575–590. doi:10.1098/rstl.1869.0021. 588페이지에 "임계점"이라는 용어가 표시됩니다.

[15] Cengel, Yunus A.; Boles, Michael A. (2002). Thermodynamics: an engineering approach. Boston: McGraw-Hill. pp. 91–93. ISBN 978-0-07-121688-3.

[16] Maslan, Frank D.; Littman, Theodore M. (1953). "Compressibility Chart for Hydrogen and Inert Gases". Ind. Eng. Chem. 45 (7): 1566–1568. doi:10.1021/ie50523a054.

[17] Emsley, John (1991). The Elements (Second ed.). Oxford University Press. ISBN 978-0-19-855818-7.

[18] Cengel, Yunus A.; Boles, Michael A. (2002). Thermodynamics: An Engineering Approach (Fourth ed.). McGraw-Hill. pp. 824. ISBN 978-0-07-238332-4.

[19] "Ammonia - NH3 - Thermodynamic Properties". www.engineeringtoolbox.com. Retrieved 2017-04-07.

[20] "Critical Temperature and Pressure". Purdue University. Retrieved 2006-12-19.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

v t 물질 상태(목록)
주	단단한 액체. 가스/증기 플라즈마
저에너지	보스-아인슈타인 응축수 페르미온 응축수 퇴화 물질 퀀텀 홀 리드버그 물질 리드버그 폴라론 이상한 일 초유체 초솔리드 포토닉 분자
고에너지	QCD 물질 격자 QCD 쿼크-글루온 플라즈마 색유리 응축수 초임계 유체
기타 주	콜로이드 유리 크리스탈 액정 시간 결정 양자 스핀 액체 이색 물질 프로그램 가능 물질 암흑 물질 반물질 자기 순서 반강자석 페리마그넷 강자석 스트링 네트 액체 슈퍼글라스
이행	끓다 비등점 응축 임계선 임계점 결정화 퇴적 증발 플래시 증발 냉동 화학 이온화 이온화 람다점 녹는 녹는점 재결합 레귤레이션 포화 유체 승화 과냉각 트리플 포인트 기화 유리화
수량	융해 엔탈피 승화 엔탈피 기화 엔탈피 잠열 잠재 내부 에너지 트라우톤의 법칙 변동성
개념	바리온 물질 바이노달 압축 유체 냉각 곡선 상태 방정식 라이덴프로스트 효과 거시 양자 현상 음펨바 효과 순서와 무질서(물리학) 스피노달 초전도 과열 증기 과열 열유전 효과

Search

임계점(열역학)

네임스페이스

더

목차

액체-증기 임계점

개요

역사

이론.

선택된 물질의 액체-증기 임계 온도 및 압력 표

혼합물: 액체-액체 임계점

수학적 정의

「」를 참조해 주세요.

각주

레퍼런스

외부 링크

Search

임계점(열역학)

액체-증기 임계점

개요

역사

이론.

선택된 물질의 액체-증기 임계 온도 및 압력 표

혼합물: 액체-액체 임계점

수학적 정의

「 」를 참조해 주세요.

각주

레퍼런스

외부 링크

「」를 참조해 주세요.