모노드로미 정리

복잡한 분석에서, 모노드로미 정리는 더 큰 집합으로 복잡한 분석함수의 분석적 지속에 관한 중요한 결과물이다.함수의 원래 영역에서 시작하여 더 큰 집합으로 끝나는 곡선을 따라 복잡한 분석 함수(여기서부터는 단순 분석 함수라고 함)를 확장할 수 있다는 생각이다.곡선 전략을 따르는 이러한 분석적 연속성의 잠재적인 문제는 더 큰 집합의 동일한 지점에 도달하는 많은 곡선이 있다는 것이다.모노드로미 정리는 거기에 도달하는 데 사용되는 곡선과 상관없이 주어진 지점에서 동일한 값을 부여할 수 있는 충분한 분석적 연속성을 위한 조건을 제공하므로, 결과적으로 확장된 분석 함수가 잘 정의되고 단일 값이 되도록 한다.

이 정리를 말하기 전에 곡선을 따라 분석적 연속성을 정의하고 그 특성을 연구할 필요가 있다.

곡선을 따라 분석 연속성

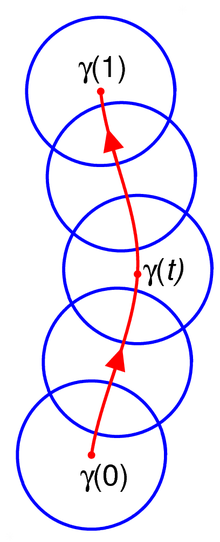
곡선을 따라 분석적 연속성의 정의는 다소 기술적인 것이지만, 기본적인 아이디어는 한 점을 중심으로 정의한 분석함수로 시작하고, 그 곡선을 덮는 작은 겹치는 디스크에 정의된 분석함수를 통해 곡선을 따라 그 기능을 확장한다는 것이다.

형식적으로 곡선(연속 함수)${\displaystyle \gamma \mathbb{}}$ :${\displaystyle }$[ 0${\displaystyle ,}$ ${\displaystyle 1}$ ${\displaystyle ]}$→ C${\displaystyle }$. ${\displaystyle$ $\$$gamma :[0,1]\to \mathb {C}.}$ $f{\displaystyle }$ ${\displaystyle$ f$}$을(를) $\gamma {\displaystyle }$ ${\displaystyle (0}$)를 중심으로$$열린 디스크 $U{\displaystyle }$ ${\$$displaystystyle$ $U$$}$에 정의된 분석 함수로 한다$$$$$.$$}$ ${\displaystyle \gamma}$을(를) 따라 페어$({\displaystyle f}$, ${\displaystyle U}$) ${\displaystyle (f,U)}$의 분석적 연속은 페어$({\displaystyle f_{}}$ , ${\displaystyle {}_{}}$ t${\displaystyle {}_{}}$)${\displaystyle (f_{t$})의$$ 모음입니다$.$$0{\displaystyle \mathrm{}}$ ${\displaystyle \le }$ ${\displaystyle t}$ ${\displaystyle \le }$ ${\displaystyle 1}$ ${\displaystyle 0\leq t\$leq t\$leq 1}$에 대한 $U_{t}:$

• ${\displaystyle f_{}}$ ${\displaystyle {0\mathrm{}}_{}}$= ${\displaystyle f}$ ${\displaystyle f_{0}=f}$ 및$$ $U{\displaystyle {}_{}}$ ${\displaystyle 0{}_{}}$= U${\displaystyle }$. ${\displaystyle U_{0}=U.}$

• 각 $t{\displaystyle }$ ${\displaystyle \in }$[ 0${\displaystyle }$, ${\displaystyle 1}$ ${\displaystyle ]}$, U ${\displaystyle t_{}}$ ${\$에 대해,$U_{t}}$은(는) γ${\displaystyle (}$t $)$ {\$displaystyle \gamma($$t$)} ${\displaystyle {}_{}}$ ${\displaystyle f_{}}$: ${\displaystyle U\mathbb{}}$ t$$→ C {\$displaystyle$f_{$t}:$에 중심을 둔 열린 디스크다$$.$U_{t}\to \mathb {C}은($는) 분석함수다$$.

• {\displaystyle t\in[0,1]}이 ε 을 존재하는 각 t 들어[0,1], 모든 카메라에 0{\displaystyle \varepsilon>0}가′t−하자 상대방과∈[0,1]{\displaystyle t'\in[0,1]}′<>ε{\displaystyle t-t의<>\varepsilon}한 가진 저γ(t′)∈ U에선{\displaystyle \gamma(to의 생략)\in U_{t}}∈. 이렇게 implies that ${\displaystyle U_{t}}$ and ${\displaystyle U_{t'}}$ have a non-empty intersection) and the functions ${\displaystyle f_{t}}$ and ${\displaystyle f_{t'}}$ coincide on the intersection ${\displaystyle U_{t}\cap U_{t'}.$$}$

곡선을 따라 이어지는 분석적 연속성의 특성

곡선을 따라 분석적 연속성은 두 개의 분석적 연속$({\displaystyle {}_{}{t}_{}}$ ,${\displaystyle {}_{}}$U ${\displaystyle t_{}}$ ) ${\displaystyle$ ($f_{$$t})$이 주어진다는 점에서 본질적으로 고유하다.$U_{t})}$ and ${\displaystyle (g_{t},V_{t})}$ ${\displaystyle (0\leq t\leq 1)}$ of ${\displaystyle (f,U)}$ along ${\displaystyle \gamma ,}$ the functions ${\displaystyle f_{1}}$ and ${\displaystyle g_{1}}$ coincide on ${\di$$splaystyle U_{1}\cap V_{1}.}$ 비공식적으로$$ $this{\displaystyle }$ ${\displaystyle$$$$\$$gamma }$을 따라${\displaystyle }$(${\displaystyle f}$ ,${\displaystyle U}$ )$${\$displaystyle$ ($f,U)}$의 모든 두 분석 연속은 $\gamma {\displaystyle }$( 1${\displaystyle }$)$$. {\$displaystysty$ \$gamma($1)의 근방에서 동일한 값으로 끝나게 된다$$$.$$}$

If the curve ${\displaystyle \gamma }$ is closed (that is, ${\displaystyle \gamma (0)=\gamma (1)}$), one need not have ${\displaystyle f_{0}}$ equal ${\displaystyle f_{1}}$ in a neighborhood of ${\displaystyle \gamma (0).}$ For example, if one starts at a point ${\displaystyle (a,0}$는 의와 같이{\displaystyle(a,0)};0{\displaystyle a>0}과 복잡한 로그의 이 점이 이웃에 정의되고 반경 γ{\displaystyle \gamma}이 원을{\displaystyle}원점(시계 반대 방향으로 엄청난 것, 0에서 여행했다){\displaystyle(a,0)}에 중심), 함으로썰 수 있습니다. 는 일화 집이 곡선을 따라 연속되는 리틱은 로그 값을${\displaystyle }$(${\displaystyle }$, ${\displaystyle 0}$) ${\displaystyle (a$$,$$0)}$에 2 $2{\displaystyle \mathrm{}}$ ${\displaystyle i}$ {\$displaystyle 2\pi$ i$}$ + 원래 값을 더한$$ 값으로 끝난다(오른쪽 두 번째 그림 참조).

모노드로미 정리

앞에서 언급한 바와 같이, 동일한 곡선을 따라 두 개의 분석 연속성은 곡선의 끝점에서 동일한 결과를 산출한다.그러나 두 개의 다른 곡선이 분석 함수가 정의되는 동일한 지점에서 분기되고, 곡선이 마지막에 다시 연결되면, 두 곡선을 따라 해당 함수의 분석 연속성이 공통 끝점에서 동일한 값을 산출한다는 것은 일반적으로 사실이 아니다.

실제로 앞 절에서와 같이 점$({\displaystyle }$ ${\displaystyle \mathrm{a}}$, ${\displaystyle 0}$) ${\displaystyle(a,0)}$과 원점 및 $반지름{\displaystyle }$ a${\displaystyle .}${\$displaystyle a.}$의 주변에 정의된 복잡한 로그도 고려할 수 있다.$$ ${\displaystyle \mathrm{그런}}$ 다음${\displaystyle }$( ,${\displaystyle }$0${\displaystyle }$) ${\displaystyle (a,0)}$에서${\displaystyle }$(${\displaystyle }$- ,${\displaystyle 0}$) ${\displaystyle (-a,0)}$까지 이$$ 원의 위쪽 반평면 호와 아래쪽 반평면 호를 시계 반대 방향으로 이동할 수 있다.${\displaystyle 이}$ 두 호를 따라 분석 연속성을 통해 얻은 (${\displaystyle }$- a${\displaystyle }$, 0${\displaystyle }$) ${\displaystyle(-a,0)$에서 로그$$ 값이 2 ${\displaystyle \pi }$ ${\displaystyle i.}$ ${\displaystyle 2\pi$ i$.}$만큼 달라진다.

그러나 시작점과 끝점을 고정된 상태로 곡선을 계속 변형시킬 수 있고 중간 곡선 각각에서 분석적 연속성이 가능하다면, 두 곡선을 따라 분석적 연속은 공통 끝점에서 동일한 결과를 산출할 것이다.이것을 모노드로미 정리라고 하며 그 진술은 아래에서 정밀하게 이루어진다.

${\displaystyle \mathrm{포인트<img\; alt="P"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/b4dc73bf40314945ff376bd363916a738548d40a"\; style="vertical-align:\; -0.338ex;\; width:1.745ex;\; height:2.176ex;"\; papago-attr-id="136">}}$ $P{\displaystyle }$$${\$displaystyle$$P$} 및${\displaystyle }$f : U$$$$→${\displaystyle }$C ${\$$U\to \mathb {C}은($는) 복합 분석 함수다$$.$Q{\displaystyle }$ ${\displaystyle Q}$을(를) 복잡한 평면의 또 다른 지점이 되도록$$ 한다.If there exists a family of curves ${\displaystyle \gamma _{s}:[0,1]\to \mathbb {C} }$ with ${\displaystyle s\in [0,1]}$ such that ${\displaystyle \gamma _{s}(0)=P}$ and ${\displaystyle \gamma _{s}(1)=Q}$ for all ${\displaystyle$$s\in [0,1],}$ the function ${\displaystyle (s,t)\in [0,1]\times [0,1]\to \gamma _{s}(t)\in \mathbb {C} }$ is continuous, and for each ${\displaystyle s\in [0,1]}$ it is possible to do an analytic continuation of ${\displaystyle f}$ along ${\di$$splaystyle \gamma _{s},$ 그러면$$ $\gamma {\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$ 및$$ $\gamma {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$1}을 따라$$$$f {\$displaystyty$ $Q$$.}$에서 동일한 값을 산출한다$$.

모노드로미 정리는 함수의 원래 영역의 한 점을 더 큰 집합의 점으로 연결하는 곡선을 통해 분석 함수를 더 큰 집합으로 확장할 수 있도록 한다.그것을 기술하는 아래의 정리(monodromy organy)라고도 한다.

${\displaystyle \mathrm{포인트<img\; alt="P"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/b4dc73bf40314945ff376bd363916a738548d40a"\; style="vertical-align:\; -0.338ex;\; width:1.745ex;\; height:2.176ex;"\; papago-attr-id="176">}}$ $P{\displaystyle }$$${\$displaystyle$$P$} 및${\displaystyle }$f : U$$$$→${\displaystyle }$C ${\$$U\to \mathb {C}은($는) 복합 분석 함수다$$.$W{\displaystyle }$ ${\displaystyle W}$이(가) $U{\displaystyle }$, ${\displaystyle U}$을(를) 포함하는 개방된 단순 연결 집합이고 $P{\displaystyle }$${\displaystyle }$, ${\displaystyle$ $W}$에서 시작하는 W ${\displaystyle$ W}에 포함된$$ $모든$ 곡선에서 $f{\displaystyle }$ ${\$$displaystystyle$ f$}$의 분석 연속성을 수행할 수 있는 경우$,$ $f$} $W{\displaystyle }$, ${\displaystyle W}$에 이어 복합 분석 함수 $g{\displaystyle }$: ${\displaystyle W\mathbb{}}$→ ${\displaystyle C}$ ${\$$U$ ${\displaystyle U}$에 대한 제한이 $f$ . ${\displaystyle f$인 W$\to \mathb {C$$}.$$}$

참고 항목

• 분석적 연속성
• 모노드로미

참조

• Krantz, Steven G. (1999). Handbook of complex variables. Birkhäuser. ISBN 0-8176-4011-8.
• Jones, Gareth A.; Singerman, David (1987). Complex functions: an algebraic and geometric viewpoint. Cambridge University Press. ISBN 0-521-31366-X.

• Triebel, Hans (1986). Analysis and mathematical physics, English ed. D. Reidel Pub. Co. ISBN 90-277-2077-0.

외부 링크

• 모노드로미 정리
• 플래닛매트릭스의 모노드로미 정리.
• 수학 백과사전 모노드로미 정리