모노드로미

복잡한 로그의 가상 부분.C \ {0}에서 복합 로그를 정의하려고 하면 서로 다른 경로를 따라 다른 답변이 제공된다.이것은 무한 순환 단조 그룹과 헬리코이드에 의한 C \ {0}의 덮개로 이어진다(리만 표면의 예).

수학에서 모노드로미는 수학적 분석, 대수적 위상, 대수적 기하학, 미분 기하학에서 나온 물체가 특이점을 "회전"하면서 어떻게 행동하는지 연구하는 학문이다.이름에서 알 수 있듯이 모노드로미의 근본적 의미는 '단독 돌기'에서 비롯된다.그것은 지도와 지도들의 반향과 밀접한 관련이 있다; 단조로운 현상을 야기하는 측면은 우리가 정의하기를 원하는 어떤 기능들이 우리가 특이점을 둘러싼 경로를 "돌리기" 때문에 단일값이 되지 않을 수도 있다는 것이다.모노드로미의 실패는 모노드로미 그룹 즉, 우리가 한 차원 "회전"할 때 일어나는 일을 암호화하는 데이터에 작용하는 변환 그룹을 정의함으로써 측정할 수 있다.모노드로미 부족을 폴리드로미라고 부르기도 한다.^[1]

정의

Let $X$ be a connected and locally connected based topological space with base point $x$ , and let $p:{\tilde {X}}\to X$ be a covering with fiber $F=p^{-1}(x)$ . For a loop $γ: [0, 1] \to X$ based at $x$ , denote a lift under the covering map, starting at a point ${\tilde {x}}\in F$ ${\tilde {x}}\in F$ , by ${\tilde {\gamma }}$ . Finally, we denote by ${\tilde {x}}\cdot {\tilde {\gamma }}$ the endpoint ${\tilde {\gamma }}(1)$ , which is generally different from ${\displaystyle {\tilde$ ${\tilde {x}}$ .There are theorems which state that this construction gives a well-defined group action of the fundamental group $π 1 (X, x)$ on $F$ , and that the stabilizer of ${\tilde {x}}$ is exactly ${\displaystyle p_{*}\left(\pi _{1}\left({\tilde {X}},{\tilde {x}}\right)\righ$ $t$ 즉, 요소 $[γ]$ 는 ${\tilde {x}}$ ~ ${\$ 에 있는 ${\tilde {X}}$ ${\tilde {X}}$ 이미지로 표현되는 $경우$ 에만 F의 점을 수정한다 ${\tilde {x}}$ 이 작용은 단조 작용이라고 $하며$ F에 있는 자동성 그룹에 해당하는 동형성 $π 1 (X,$ $x)$ → $오토(H * (F x)$ 는 대수적 단조 작용이다.이 동형성의 이미지는 단조로운 집단이다.위상 모노드로미 그룹이라고 하는 다른 지도 $map 1 (X,$ $x)$ → $Diff(F x)/Is(F x)$ 가 있다.

예

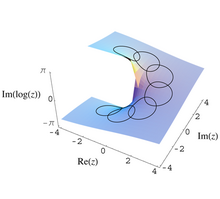
이러한 생각들은 복잡한 분석에서 처음으로 명백하게 만들어졌다.분석적 연속성 과정에서 구멍이 난 복합 평면 $plane$ $\ {0}$ 의 일부 열린 부분집합 $E$ 에서 분석 $함수$ F( $z)$ 인 함수는 $E$ 로 다시 이어질 수 있지만 값이 다를 수 있다.예를 들어, 다음을 수행하십시오.

{\begin}F(z)&=\log(z)\\E&=\{z\in \mathb {C} \mid \operatorname {Re}(z)>0\}\end{arged}}}

그런 다음 시계 반대 방향으로 원을 돌면서 계속 분석

z =1

$F (z)$ 가 아닌 반환으로 귀결될 것이다.

F(z)+2\pi i}

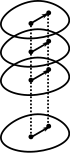
이 경우 모노드로미 그룹은 무한 순환이며 피복 공간은 구멍이 난 복합 평면의 범용 커버가 된다. $이$ 커버는 helic > $0$ 으로 제한되는 헬리코이드(헬로이드 기사에서 정의함)로 시각화할 수 있다.피복 지도는 수직 투영으로, 어떤 의미에서 구멍이 뚫린 평면을 얻기 위한 분명한 방법으로 나선형을 붕괴시키는 것이다.

복합영역의 미분방정식

한 가지 중요한 적용은 미분방정식에 대한 것이다. 여기서 단일 용액은 분석적 연속성에 의해 더 선형적으로 독립된 솔루션을 제공할 수 있다.복합 평면의 개방되고 연결된 집합 S에 정의된 선형 미분 방정식은 단조직을 가지며, 이는 (더 정밀하게) S의 기본 집단을 선형적으로 표현한 것이며, S 내의 모든 분석 연속 원형 루프를 요약한 것이다.(정규적인 특이점들로) 방정식을 구성할 때 나타나는 역 문제를 리만-힐버트 문제라고 한다.

일반 선형 시스템(특히 Fuchsian)의 경우, 일반적으로 단조 그룹의 생성기로서 각 루프에 해당하는 연산자_j M을 선택하며, 이 연산자 M은 시계 반대 방향으로 시스템의 극 중 하나만 우회한다.If the indices j are chosen in such a way that they increase from 1 to p + 1 when one circumvents the base point clockwise, then the only relation between the generators is the equality $M_{1}\cdots M_{p+1}=\operatorname {id}$ . The Deligne–Simpson problem is the following realisation problem:GL(n, C)에 있는 결합 등급의 어떤 튜플이 상기 관계를 만족하는 이들 등급의 매트릭스 M의_j 수정 불가능한 튜플이 존재하는가?이 문제는 피에르 들랭에 의해 공식화되었고 카를로스 심슨은 이 문제를 해결하기 위한 결과를 얻은 첫 번째 사람이었다.Fuchsian 시스템의 잔류물에 관한 문제의 추가 버전은 Vladimir Kostov에 의해 공식화되고 탐구되었다.이 문제는 GL(n, C) 이외의 매트릭스 그룹에 대해서도 다른 저자들에 의해 검토되었다.^[2]

위상학적 및 기하학적 측면

커버 맵의 경우, 특별한 경우로 보고 호모토피 리프팅 특성을 이용하여 커버 C로 들어올릴 때 베이스 공간 X의 경로를 "따라"(단순함을 위해 경로로 연결된 것으로 가정함)한다.x 위의 c에서 시작하기 위해 들어올린 x in X에 기초한 루프를 따라간다면, 우리는 x 위의 c*에서 다시 끝날 것이다; c c c*에서, 그리고 이 루프를 코딩하기 위해 모든 c의 집합에 있는 순열 그룹으로서 $π$ ₁(X, x)의 작용을, 이 맥락에서 단조 그룹으로서 고려한다.

차동 기하학에서 유사한 역할은 병렬 전송에 의해 수행된다.매끄러운 다지관 M 위에 있는 주요 번들 B에서 연결은 M에서 M 위의 섬유로부터 인접한 섬유로 "수평적" 이동을 허용한다.m에 기초하여 루프에 적용할 때 효과는 m에 섬유 변환의 홀노노미 그룹을 정의하는 것이다. B의 구조 그룹이 G인 경우, 제품 번들 M × G에서 B의 편차를 측정하는 것은 G의 하위 그룹이다.

모노드로미 그룹화 및 분파

기지의 한 경로는 그것을 들어올리는 전체 공간에 경로가 있다.이러한 경로를 따라 밀면 기본 그룹형에서 모노드로미 효과를 얻을 수 있다.

기본 groupoid와 유사하게 기준점의 선택을 없애고 단조로운 groupoid를 정의할 수 있다. $p:{\tilde {X}}\to X$ 서는 진동 p $p:{\tilde {X}}\to X$ : $p:{\tilde {X}}\to X$ ~ $p:{\tilde {X}}\to X$ → $p:{\tilde {X}}\to X$ $p:{\tilde{X}\to X$ 의 기본 공간 X 경로의 (호모토피 클래스) 리프트를 고려한다 $p:{\tilde {X}}\to X$ 결과는 기본 공간 X 위에 그룹오이드의 구조를 가진다.장점은 X의 연결 상태를 떨어뜨릴 수 있다는 것이다.

게다가 건설은 다음과 같은 방법으로 일반화될 수 있다. $(M,{\mathcal {F}})$ , $(M,{\mathcal {F}})$ ) $(M,{\mathcal{F})$ a $(M,{\mathcal {F}})$ (단수일 가능성이 있음) M의 구분을 고려하십시오. ${\mathcal {F}}$ 다음 F ${\$ 의 잎에 있는 모든 경로에 대해 ${\mathcal {F}}$ 엔드포인트를 통과하는 국소 횡단 섹션에 유도된 차이점형성을 고려할 수 있다.단순하게 연결된 도표 안에서 이 차이점형성은 엔드포인트 주변의 차이점형성의 생식기로 넘어가면 서로 다른 횡단 부분들 사이에서 독특하고 특히 표준적이 된다.이러한 방식으로 단순하게 연결된 차트 내의 경로(고정된 엔드포인트 사이)에서도 독립적이 되며 따라서 호모토피에서는 불변한다.

갈루아 이론을 통한 정의

F(x)는 다항 링 F[x]의 분수 필드인 F 필드 위에 변수 x의 합리적인 함수 필드를 나타낸다.요소 y = F(x)의 f(x)는 유한 자기장 확장 [F(x) : F(y)]를 결정한다.

이 확장은 일반적으로 갈루아가 아니라 갈루아 폐쇄 L(f)를 가지고 있다.확장자의 관련 갈루아 그룹[L(f) : F(y)]을 f의 모노드로미 그룹이라고 한다.

F = C 리만 표면 이론의 경우, 위에 주어진 기하학적 해석을 허용한다.확장자 [C(x) : C(y)]가 이미 갈루아인 경우, 관련 모노드로미 그룹을 갑판 변형 그룹이라고 부르기도 한다.

이것은 리만 존재 정리로 이어지는 공간을 커버한다는 갈루아 이론과 관련이 있다.

참고 항목

메모들

^ König, Wolfgang; Sprekels, Jürgen (2015). Karl Weierstraß (1815–1897): Aspekte seines Lebens und Werkes – Aspects of his Life and Work (in German). Springer-Verlag. pp. 200–201. ISBN 9783658106195. Retrieved 5 October 2017.
^ V. P. Kostov (2004), "The Deligne–Simpson problem — a survey", J. Algebra, 281 (1): 83–108, arXiv:math/0206298, doi:10.1016/j.jalgebra.2004.07.013, MR 2091962, S2CID 119634752 그리고 그 안에 있는 참고자료들도.

참조

V. I. Danilov (2001) [1994], "Monodromy", Encyclopedia of Mathematics, EMS Press
"그룹-그룹화 및 모노드로미 그룹화", O. Muccuk, B. Kılısarslan, T. ¸Sahan, N. Allemdar, 토폴로지 및 애플리케이션 158(2011) 2034–2042 doi:10.1016/j.topol.12011.06.048
R. Brown Topology 및 Groupoids(2006).
P.J. 히긴스 "카테고리·그룹로이드", 판 노스트랜드(1971) TAC 재인쇄

[König2015-1] König, Wolfgang; Sprekels, Jürgen (2015). Karl Weierstraß (1815–1897): Aspekte seines Lebens und Werkes – Aspects of his Life and Work (in German). Springer-Verlag. pp. 200–201. ISBN 9783658106195. Retrieved 5 October 2017.

[2] V. P. Kostov (2004), "The Deligne–Simpson problem — a survey", J. Algebra, 281 (1): 83–108, arXiv:math/0206298, doi:10.1016/j.jalgebra.2004.07.013, MR 2091962, S2CID 119634752 그리고 그 안에 있는 참고자료들도.

[1]

[2]

Search