무어 기계

계산 이론에서 무어 기계는 현재의 출력 값이 현재의 상태에 의해서만 결정되는 유한 상태 기계입니다.이는 현재 상태와 입력 값에 의해 모두 출력 값이 결정되는 Mailey 기계와는 대조적입니다.다른 유한 상태 기계와 마찬가지로 무어 기계에서도 일반적으로 입력이 다음 상태에 영향을 미칩니다.따라서 입력은 간접적으로 후속 출력에 영향을 줄 수 있지만 현재 또는 즉시 출력에는 영향을 미치지 않습니다.무어 머신의 이름은 Edward F의 이름을 딴 것입니다. 무어는 1956년 "시퀀셜 ^[1]머신에 대한 게단켄 실험"이라는 논문에서 이 개념을 제시했다.

형식적 정의

무어 머신은 다음과 같이 구성된6개의 태플$({\displaystyle {}_{},}$ ${\displaystyle {q\mathrm{}}_{}}$ 0${\displaystyle {}_{}}$ ${\displaystyle \mathrm{\sigma },}$ ${\displaystyle O,}$ $、$ ${\displaystyle G}$ ) { $display$style ($Q,q_{0},\Sigma,O,\delta,G)}$로 정의할 수 있습니다.

• 유한 $상태{\displaystyle }$ Q$(\displaystyle$ Q$)$
• 시작 상태(초기 $상태$라고도 함) ${\displaystyle {q\mathrm{}}_{}}$0({$displaystyle q_{$0$$$})$ Q({$displaystyle$Q})의 $요소{\displaystyle }$
• 입력 알파벳$\delta {\displaystyle \mathrm{}}$(\$displaystyle \Sigma)$라고 하는 유한 집합
• 출력 $알파벳{\displaystyle }$ O$(\displaystyle$ O$)$라고 하는 유한 집합
• ${\displaystyle \mathrm{전이}}$ 함수 ${\displaystyle :}$ :${\displaystyle }$Q × ${\displaystyle \sigma }$ ${\displaystyle \to }$Q \ $displaystyle \$$displays$ :$Q\times$ \$Sigma \right$ 화살표$$Q}가 상태와$$ 입력 알파벳을 다음 상태로 매핑합니다.
• 각 상태를 출력 알파벳에 매핑하는 출력 $함수{\displaystyle }$G : ${\displaystyle Q}$ ${\displaystyle \to }$ {\$displaystyle$ G$:Q$$\right 화살표$ O$}$

무어 머신은 유한 상태 변환기의 제한된 타입으로 간주할 수 있다.

시각적 표현

테이블

상태 전이 $테이블$은 전이 관계 ${\displaystyle :}$ :${\displaystyle Q}$ × →$$ ${\displaystyle Q}$ \ $displaystyle \$$disples$ :$Q\times$ \$Sigma \right 화살표$Q.

도표

무어 머신의 상태 다이어그램 또는 무어 다이어그램은 출력 값을 각 상태와 연관짓는 다이어그램 상태 다이어그램입니다.

Maly 머신과의 관계

Moore 머신과 Mailey 머신은 모두 유한 상태 머신의 유형이기 때문에 표현력이 동등합니다.어느 타입이든 정규 언어를 해석하는데 사용할 수 있습니다.

Moore 머신과 Mailey 머신의 차이점은 후자의 경우 전환의 출력은 현재 상태와 전류 $$의 조합($G$의 $도메인$으로서$$S ${\displaystyle \times }$ \$displaystyle$ S$\times \Sigma)$$$에 의해 결정되며, 현재 상태($$으로서 S$\displaystyle$ S$\$tima$)$에 의해 결정된다는 점이다.$f{\displaystyle }$G \ $displaystyle$ G$$} 。상태 다이어그램으로 나타낼 경우,

• 무어 머신의 경우 각 노드(상태)에 출력값으로 라벨이 부착됩니다.
• Mealy 기계의 경우 각 호(전이)에 출력 값으로 레이블이 지정됩니다.

모든 Moore $머신{\displaystyle }$M(\$displaystyle$M)은$$ 상태 및 전환이 동일한 Maly 머신과 동등하며 출력 $함수{\displaystyle }$G$($ ${\displaystyle )}$ ) ${\displaystyle =}$ ${\displaystyle G_{}}$($m$M ( ${\displaystyle s}$ ,$$ )$= G_{M}(\sigma$ ) （ $delta$_{$M(s$ , ${\displaystyle s}$ ; s )$）$。${\displaystyle G_{}}$M ( ${\displaystyle m{}_{}}$M (${\displaystyle s}$ , ${\displaystyle )}$)$${ $displaystyle G$_ { $M$} ( \ $delta$_ { $M }$ , \ $sigma )$} 。${\displaystyle {여기}_{}}$서 G$$M ( \ $displaystyle$G$_$ {$M$ } )은$$M ( \ $displaystyle$\ $delta _$ {$$M$\})$의 출력 함수이고, ${\displaystyle m_{}}$ M$$( \ displaystyle \ $delta$ _ m $)$는 M )입니다.

단, 모든 Maley 머신이 동등한 Moore 머신으로 변환되는 것은 아닙니다.일부는 거의 동등한 Moore 기계로만 변환할 수 있으며, 출력은 시간 내에 전환됩니다.이는 상태 라벨이 변환 라벨과 쌍을 이루어 입력/출력 쌍을 형성하는 방식 때문입니다.$상태{\displaystyle {}_{}}$({$displaystyle s_{i$})에서$$ $상태{\displaystyle {}_{}}$ $({$j$\})$로 i ${\displaystyle {}_{}}$ ${\displaystyle s_{}}$j(\$displaystyle s_{i}\rightarrow s_{j$})의$$ $전환$을 검토합니다.${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ s ${\displaystyle j_{}}${$displaystyle s_{i}\rightarrow s_{$$j}}$ 의$$ 입력에$$엣지( ${\displaystyle s_{}}$i , ${\displaystyle s_{}}$j $)$의 라벨이 붙어 $있습니다.$이 입력에 대응하는 출력은 $상태{\displaystyle {}_{}}$ ${\displaystyle s_{}}$의 $라벨$입니다$.$^[2]$이것$은 이행의 소스 상태임을 주의해 주십시오$.$따라서 각 입력에 대해 출력은 입력이 수신되기 전에 이미 고정되어 있으며 현재 상태에 따라 달라집니다.이것은 E에 의한 원래의 정의입니다.무어. 전환 ${\displaystyle s_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle s_{}}$j \ $displaystyle$ s _ { $i$} \ $rightarrow$ s$_$ { j$\}$ 의 출력으로서 ${\displaystyle {state}_{}}$ s$${ \ $displaystyle s$_ { $j$$$} 의$$ 라벨을 사용하는 것은 일반적인 실수입니다.

예

입력/출력 수에 따라 유형을 지정합니다.

간단하죠.

심플 무어 머신에는 입력과 출력이 각각1개씩 있습니다.

• XOR을 사용한 에지 검출기
• 이진 가산기
• 클럭된 시퀀셜 시스템(글로벌 클럭 신호가 변경되었을 때만 상태가 바뀌는 무어 머신의 제한된 형식)

대부분의 디지털 전자 시스템은 시계식 순차 시스템으로 설계되어 있습니다.클럭된 시퀀셜 시스템은 무어 머신의 제한된 형태로, 글로벌 클럭 신호가 변경되었을 때만 상태가 변경됩니다.일반적으로 현재 상태는 플립 플랍에 저장되며 글로벌 클럭 신호는 플립 플랍의 "클럭" 입력에 연결됩니다.시계식 순차 시스템은 전이성 문제를 해결하는 한 가지 방법입니다.전형적인 전자 무어 기계는 현재 상태를 출력(lambda)으로 디코딩하는 조합 논리 체인을 포함한다.현재 상태가 변경되는 순간 이러한 변경은 체인을 통해 전파되며 거의 즉시 출력이 업데이트됩니다.변경 내용이 체인을 통과하는 동안 출력에 결함이 발생하지 않도록 하기 위한 설계 기법이 있지만 대부분의 시스템은 짧은 전환 시간 동안 결함이 무시되거나 관련이 없도록 설계되었습니다.그러면 무어 기계의 상태가 다시 바뀔 때까지 출력이 무한정 동일하게 유지됩니다(LED는 밝게 유지되고, 전원은 모터에 연결된 상태로 유지되며, 솔레노이드는 통전 상태로 유지되는 등).

작업 예

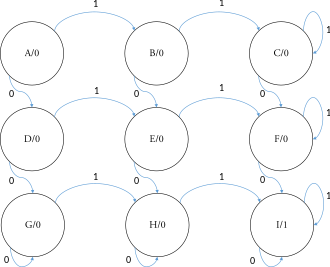
시퀀셜 네트워크는 1개의 입력과 1개의 출력을 가진다.적어도 2개의 0과 2개의 1이 입력으로 발생하면 출력은 1이 되고 그 후에 1을 유지합니다.

위의 설명은 9개 주를 가진 무어 기계 오른쪽에 표시된다.그 초기 상태는 국유 A, 최종 상태가 상태입니다.이 예에 대한 상태 테이블:그를 따릅니다.

현재 상태	입력	다음 주	산출량
A	0	D	0
	1	B
B	0	E	0
	1	C
C	0	F	0
	1	C
D	0	G	0
	1	E
E	0	H	0
	1	F
F	0	I	0
	1	F
G	0	G	0
	1	H
H	0	H	0
	1	I
I	0	I	1
	1	I

복잡한

더 복잡한 무어 기계 다중 입력뿐만 아니라 다중 출력이 있을 수 있다.

게단켄 실험

무어의 1956년 논문에서{S\displaystyle}n{n\displaystyle}주 있다는 것으로 정의되는(n, m안 내려){\displaystyle(n, m안 내려)}오토 머터(이나 기계)S, 치고{m\displaystyle}입력 상징과 동업-{p\displaystyle}출력 기호"순차적 머신에 Gedanken-experiments"[1].9정리 S{S\displaystyle}의 구조에 대해 S을 대상으로 실험을{S\displaystyle}. 나중에"S{\displaystyle S}기계""무어 기계"로 알려지게 된 입증된다.

이 문서의 마지막 섹션 "기타 문제"에는 다음과 같은 작업이 명시되어 있습니다.

직접적으로 뒤따르는 또 다른 문제는 정리 8과 9에서 주어진 경계의 개선이다.

무어의 정리 8은 다음과 같이 공식화된다.

$임의$의${\displaystyle }$(${\displaystyle n}$${\displaystyle }$;${\displaystyle m}$ ;${\displaystyle p}$) \ $displaystyle ( n$ ; m ;$p$ ) \ $displaystyle S$\$$displaystyle S \ displaystyle S \ $displaystyle$$（$$n$ ; m ; p ） $an$ ( given ( ( ( ( ( ( ( ( ( ( ( ( （ n - ${\displaystyle \frac{1}{}}$）$$ \ $displaystyle$ $2{\displaystyle \frac{}{}}$ $(imentimentiment$ ( ( (imentimentimentiment ( ($n$ - 2 lengthimentimentimentimentimentimentimentimentimentiment2 lengthiment2 $imentimentimentimentimentimentimentiment2$ imentimentimentimentimentimentd. 실험의 d.

1957년, A. A. 카라츠바는 다음과 같은 두 가지 이론을 증명하였고, 이는 무어의 "테오렘 8"의 실험 길이 한계 개선에 대한 문제를 완전히 해결하였다.

정리 A$(\displaystyle$ S$)$가${\displaystyle }$($;m;p)$ 기계이며, 각각의 상태가 서로 구별 가능한 경우$,{\displaystyle \frac{}{}}$ 최대 길이(${\displaystyle \frac{n}{}}$-${\displaystyle \frac{1}{}}$) (${\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \frac{-2}{}}$)${\displaystyle }$2 +$$ ({$displaystyle {n-1)$ ($n-2)$ + 1 (\$displaystyle$ {n-2] (n-2) {$2-1$}) ${+$1} {\displaystyle(으)} {n$$;p$}$ {n;p}}}} {$n$$;$p$}}}}}}}}$의 분기 실험이 존재합니다$.$S$(\displaystyle$ S$)$를 $선택$합니다.

정리 B$)$ (\$displaystyle (n;m;p)$ 기계가$$ 존재하며, 각각의 두 상태는 서로 구별이 가능하여 실험 종료 시 기계 상태를 결정하는 가장 짧은 실험의 길이는 (${\displaystyle \frac{n}{}}$ ${\displaystyle \frac{-1)}{}}$ (${\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \frac{-}{}}$ ${\displaystyle \frac{2}{}}$)${\displaystyle }$2 +$$ (\$displaystyle$ {$tfrac {n-1)$ + 1 ($n-2)${\displaystyle} {n-1$}}$ {\displaystyle (n;m;p}이다.

이론 A와 B는 1958년 모스크바 주립대학 기계학과 수학과 학생 작품 경진대회에서 추천 참고 문헌을 통해 구별된 4학년 A. A. 카라츠바의 "자동화 이론으로부터의 문제에 대하여"의 기초가 되었다.카라츠바의 논문은 Uspekhi Mat 저널에 게재되었다. 1958년 12월 17일에 Nauk가 그곳에서 ^[3]1960년 6월에 출판되었다.

현재(2011년)까지 실험 길이에 대한 카라추바의 결과는 오토마타 이론과 계산 복잡도 이론의 유사한 문제 모두에서 유일한 정확한 비선형 결과이다.

「 」를 참조해 주세요.

• 동기 회로
• 밀리머신
• 알고리즘 상태 기계
• 자율 시스템(수학)

레퍼런스

추가 정보

• Conway, J.H. (1971). Regular algebra and finite machines. London: Chapman and Hall. ISBN 0-412-10620-5. Zbl 0231.94041.
• 무어 E. F. 게단켄-시퀀셜 머신 실험오토마타 연구, 수학 연구 연보, 34, 129–153.프린스턴 대학 출판부, 프린스턴, 뉴저지 주(1956)
• 카라츠바 A.A. 유한 오토마타 이론의 한 가지 문제 해결.Up. Mat. Nauk, 157-3, 157-159(1960).
• 카라츠바 A.A. Experimente mit Automaten(독일) Electron.정보 버전카이버네틱, 11, 611-612(1975).
• 카라츠바 A. A. 연구 작업 목록

무어 앤드 밀리 머신

외부 링크

• Wikimedia Commons의 Moore 머신 관련 미디어