판 시터트-제르니케 정리

이 문서에는 여러 가지 문제가 있습니다.개선을 돕거나 토크 페이지에서 이러한 문제에 대해 논의해 주십시오.(이러한 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다) 이 기사는 독자들에게 혼란스럽거나 불분명할 수 있다. 글의 명확화를 도와주세요. 토크 페이지에 이 건에 대한 논의가 있을 수 있습니다.(2011년 2월) (이 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다) 이 문서에는 일반적인 참조 목록이 포함되어 있지만 대응하는 충분한 인라인 인용이 없습니다. 좀 더 정확한 인용문을 도입하여 이 기사의 개선에 도움을 주십시오. (2011년 2월) (이 템플릿메시지의 삭제 방법 및 삭제 타이밍에 대해 알아보기) (이 템플릿메시지를 삭제하는 방법과 타이밍을 확인합니다)

물리학자 피터 헨드리크 반 시터트와 프리츠 제르니케의 이름을 딴 반 시터트-제르니케 정리는 일정한 조건 하에서 멀리 있는 비일관성 선원의 강도 분포 함수의 푸리에 변환이 그것의 복잡한 가시성과 동일함을 나타내는 일관성 이론의 공식이다.이는 비일관성 소스의 파면이 먼 거리에서 대부분 일관되게 나타날 것임을 의미합니다.직관적으로 이것은 두 개의 일관성이 없는 선원에 의해 생성되는 파동을 고려함으로써 이해할 수 있다.소스 중 하나 바로 앞에서 파면을 측정하면 측정이 인근 소스에 의해 지배됩니다.소스에서 멀리 떨어진 곳에서 동일한 측정을 수행하면 측정값이 더 이상 단일 소스에 의해 좌우되지 않습니다. 두 소스는 모두 장거리 파면에 거의 동일하게 기여합니다.

이 추론은 잔잔한 연못 중앙에 두 개의 돌을 떨어뜨리면 쉽게 이해할 수 있다.연못의 중앙 부근에서는 두 개의 돌에 의해 야기되는 소동은 매우 복잡할 것이다.그러나 이 교란이 연못 가장자리를 향해 확산되면서 파도는 잔잔해지고 거의 원형으로 보일 것이다.

반 시터트-제르니케 정리는 전파 천문학에 중요한 의미를 갖는다.맥동과 매저를 제외한 모든 천문학적 근원은 공간적으로 일관성이 없다.그럼에도 불구하고, 그것들은 반 시터트-제르니케 정리를 만족시킬 만큼 충분히 큰 거리에서 관찰되기 때문에, 이 물체들은 영상 평면의 다른 지점에서 0이 아닌 정도의 일관성을 보인다.전파천문자는 천체영상평면(이른바 '시야함수')의 다른 점에서의 일관성을 측정함으로써 광원의 휘도분포를 재구성하고 광원의 외관을 2차원 맵으로 만들 수 있다.

정리서

둘 다 시선에 수직인 두 개의 매우 먼 평행 평면을 고려하여 소스 평면과 관측 평면이라고 합니다. 만약 ${\displaystyle {\mathrm{\delta }}_{}}$ ${\displaystyle \mathrm{12}}$ ${\displaystyle {}_{}u}$ ,${\displaystyle }$v , ${\displaystyle 0}$) { $displaystyle$ \$Gamma _$ { $12 （ u$ , v , $0$） } 이$$ 관측 평면 내의 두 점 사이의 상호 일관성 함수라면, 그 다음

$\Displaystyle \Gamma _{12}(u,v,0)=\iint I(l,m)e^{-2\pi i(ul+vm)},dl,dm}$

$여기$서$$l {$displaystyle$ l$}$ 및$m{\displaystyle }$ {$displaystyle$ m$}$은 소스 평면에서 먼 소스에 있는 점의 방향 코사인이고, u$${$displaystyle$u} 및$$$$v {$displaystyle$ v$}$는 각각 파장 및 I $단위$로 관측 평면에 있는 두 관측점 사이의 x 거리와 y 거리입니다.${\displaystyle$ I$}$은 ^[1]소스의 강도입니다.이 정리는 1938년 ^[3]Frits Zernike가 제공한 더 간단한 증거와 함께 1934년 Pieter Hendrik van^[2] Cittert에 의해 처음 도출되었다.

이 정리는 통계적 특성과 단순한 상관관계 또는 심지어 공분산 처리 방법과의 차이 때문에 일부 엔지니어나 과학자들에게는 혼란스러운 상태로 남을 것이다.207페이지부터 시작하는 ^[4]Goodman은 좋은 참고 자료(일부 사용자에게는 여전히 문제를 명확하게 설명하지 못할 수 있지만 메서드를 반영할 수 있는 훌륭한 스케치를 가지고 있습니다)입니다.

상호 일관성 함수

관측 평면(이것을 1과 2라고 함)의 두 지점에서 측정된 일부 $전계{\displaystyle }$ E$(t)$에 대한$$ 상호 일관성 함수는 다음과 같이 정의된다.

$\displaystyle \Gamma _{12}(\display)=\lim _{T\to\infty}{\frac {1}{2T}}\int _{-T}^{T}E_{1}(t)E_{2}^*}(t-\tau)dt}$

$여기$서 $§$ {$displaystyle \tau}$은 관측$$ 지점 1과 2에서 E$(t)$ 측정 $사이$의 시간 오프셋입니다.두 지점에서의 필드 상호간 간섭성은 $\displaystyle$$tau$로 시간적으로 분리된 두 지점에서의 전계간 시간평균 교차상관이라고 생각할 수 있습니다.따라서 완전히 일관성이 없는 두 선원을 관찰할 경우 두 지점 사이의 상호 간섭 함수는 상대적으로 작을 것으로 예상해야 합니다.관측 평면의 ndom 점. 소스가 건설적으로뿐만 아니라 파괴적으로 간섭하기 때문입니다.그러나 관측된 필드의 합계는 어느 두 지점에서나 거의 같기 때문에 소스와는 거리가 먼 상호 일관성 함수가 상대적으로 클 것으로 예상해야 한다.

두 전기장의 강도 제곱근 곱에 대한 상호 일관성 함수의 정규화는 복잡한 수준의 (2차) 일관성(상관 계수 함수)을 산출한다.

$\displaystyle \{12}(\displaystyle )=blac {Gamma _{12}(\displayrt {I_{1}}}{\sqrt {I_{2}}}}}}$

정리의 증명

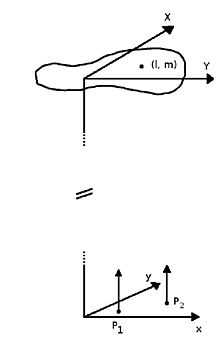
${\displaystyle X}$ Y$(\displaystyle$XY)와 x $(\displaystyle$ xy$)$를 각각 소스 평면과 관찰 평면의 데카르트 좌표로 $합니다{\displaystyle }$.소스 평면의 소스로부터 발생하는 전계가 관찰 평면의 $({$ P_${1})$과 $({$의 두 지점에서 측정된다고 가정합니다.소스 내 점의 위치는 방향 코사인$({\displaystyle l}$ ,${\displaystyle m}$) {$displaystyle ( l$ , $m$)$$。(소스가 멀리 떨어져 있기 때문에 $({$ P_${1})$에서 $({$}})와 방향이 같아야 합니다.$$${\displaystyle {그런\mathrm{}}_{}}$ 다음 P 1$({$ P_${1})$에서 측정된 전계를 페이저를 사용하여 기록할 수 있습니다.

${\displaystyle E_{1}(l,m,t)=A\left(l,m,t-{\frac {R_{1}}{c}}\right}{\frac {e^{-i\Omega\left(t-{\frac {R_{1}}}}\frac {R_{1}}}}}}}\right}}$

${\displaystyle {여기}_{}}$서 R 1$({$은 소스로부터 ${\displaystyle {P\mathrm{}}_{}}$1({$displaystyle P_{1$까지의 거리이고$,$ $\delta {\displaystyle }$({$displaystyle \obe})$는 빛의 각 $주파수$이며$,$ A({$displaystyle$ A$})$는 전계의 복소 진폭입니다.마찬가지로 $({$에서 측정된 전계는 다음과 같이 쓸 수 있습니다.

${\displaystyle E_{2}(l,m,t)=A\left(l,m,t-{\frac {R_{2}}{c}}\right}{\frac {e^{-i\Omega\left(t-{\frac {R_{2}}{c}}}}\frac {R_{2}}}}}}}\right}}}$

이제 $({$과 $({$ 사이의 시간 평균 교차 상관 관계를 계산합니다.

${\displaystyle {\big \m,t}E_{2}^{*}(l,m,t){\big \rangle}=(\big \langle }A\left(l,m,t-{\frac {R_1}}{c}\오른쪽)A^{*}\left(l,m,t-{\frac {R_{2}}{c}}\right){\Bigg \rangle } \ times { e ^ { i \ omega { { frac { R _ { { c } } } } { R _ { } } } \ times { frac { e ^ { - i \ omega { r _ { c } } } } } } } { R _ rames }$

각도 괄호 내의 양은 시간 평균화되므로 양쪽 모두에 동일한 오프셋이 추가되는 한 진폭의 시간 기간에 대한 임의의 오프셋을 추가할 수 있습니다.이제 R ${\displaystyle \frac{{}_{}}{}}$c(\${R_{1}}$ {$c})$를 두 진폭의 시간 항에 $추가$합니다.따라서 두 지점에서 전기장의 시간 평균 교차 상관관계는 다음과 같이 단순화됩니다.

${\displaystyle\big\m,t}E_{2}^{*}(l,m,t){\big \rangle}=\bigg \m,t}A(l,m,t)A^{*}\left(l,m,t-{\frac {R_{2}-R_{1}}{c}}\right) {\Bigg \rangle } \ times { frac { e ^ { i \ 메가 \ left （ \ frac { R _ { 1 } - R _ {2} } } } } { R _ { { { 1} R _ { } } } } } { R _ { right } } } }$

단, 소스가 원거리 필드에 있는 경우 ${\displaystyle {R\mathrm{}}_{}}$ 1$(\$과 ${\displaystyle {R\mathrm{}}_{}}$ 2$(\$의 차이는 빛이 시간$t{\displaystyle }$(\$displaystyle$ t$)$로 이동하는 거리에 비해 $.(\displaystyle$t는 역대역폭과 같은 순서입니다).따라서 이 작은 보정은 무시될 수 있으며, ${\displaystyle {P1\mathrm{}}_{}}$$({$ P_${$1$$$})$과 P2$({$displaystyle P_${2$})에서의 전기장 상호 상관 표현은 더욱 단순해집니다.

$\displaystyle E_{1}(l,m,t)E_{2}^{*}(l,m,t)\rangle =\displayle A(l,m,t)A^{*}(l,m,t)\rangle \times \times {e^{i\Omega \left({\frac {R_{1}-R_{2}}{c}}}}}{R_{1}R_{2}}}}}}}}$

${\displaystyle \mathrm{여기}}$서${\displaystyle }$A${\displaystyle }$(${\displaystyle l}$ ,${\displaystyle m}$ ,${\displaystyle t}$ ) ${\displaystyle {}^{}}$(${\displaystyle l}$ ,${\displaystyle m}$ ,${\displaystyle t}$ )${\$ \ $display$ \ $langle$A ($l$ , m ,$$$t$ )$A^{*}(l,m,t)\rangle$}은$$ 단순히 특정 $포인트$에서의 소스 강도${\displaystyle I(l,}$m$)\displaystyle I(l,$m$)\}$입니다.따라서 상호 상관 표현은 다음과 같이 더욱 단순해집니다.

$\displaystyle E_{1}(l,m,t) E_{2}^{*}(l,m,t)\rangle = I(l,m){\frac {e^{i\Omega \leftflac\frac {R_{1}-R_{c}}}{R_1}}{{1}}}}}{{R,{{1}}}}}}}}}}}}{{{{R,}}}}}}}}}},{R,{R,{R,{R,}}}}},{R,$

이 식에서 상호 일관성 함수를 계산하려면 전체 소스에 걸쳐 적분하기만 하면 됩니다.

$\displaystyle \Gamma _{12}(u,v,0)=\int _{\textrm {source}}I(l,m){\frac {e^{i\opega \left({\frac {R_{1}-R_{2}}}{c}}\right}}}{R_{2}},dS}$

${\displaystyle {A\mathrm{}}_{}}{\displaystyle }$1 (${\displaystyle l}$ ,${\displaystyle m}$ ,${\displaystyle t}$ )${\displaystyle {A\mathrm{}}_{}^{}}$ 2${\displaystyle {}_{}{}_{}^{}l}$ ,${\displaystyle m}$ , ${\displaystyle t）⟩}${ $displaystyle \langle A_{1$} ($l$ ,$m$ ,$$$t$ )형식의 크로스텀에 주의해 주세요.$A_{2}^{*}(l,m,t)\rangle}$은 소스가$$ 일관성이 없다고 가정하여 포함되지 않습니다.따라서 소스로부터 다른 두 점 사이의 시간 평균 상관 관계는 0이 됩니다.

그런 다음${\displaystyle u,}$ ${\displaystyle v}$, l$,$ {\$displaystyle u$, $v,$ l$$}$및{\displaystyle }$ m(\$displaystyle$ m$\})$을 ${\displaystyle {사용}_{}}$하여 R${\displaystyle {}_{}{}_{}}$ - ${\displaystyle {R\mathrm{}}_{}}$1(\$displaystyle$ $R_{2}-R_$${$1}-{1}) 용어를$$ 다시 씁니다. 이 $작업$을 ${\displaystyle {수행}_{}}$하려면 P 1${\displaystyle {}_{}}$ (${\displaystyle {}_{}{x\mathrm{}}_{}}$ 1, ${\displaystyle {y\mathrm{}}_{}}$1) (\$displaystyle$ P_${1}$= ($x{\displaystyle {}_{}}$$$1) 및 ${\displaystyle {2\mathrm{}}_{}}$ ) }${\displaystyle }$$=$ (2) ） ${\displaystyle {}_{}}$ (${\displaystyle 2_{}}$ ) ） 。이것으로 알 수 있다.

${\displaystyle R_{1}=sqrt {R^{2}+x_{1}}^{2}+y_{1}^{2}}}\,}$

${\displaystyle R_{2}=sqrt {R^{2}+x_{2}}^{2}+y_{2}^{2}}}\,}$

$여기$서 R$${\$displaystyle$ R$}$은 관측 평면의 중심과 선원의 중심 사이의 거리입니다.${\displaystyle {R\mathrm{}}_{}}$ 1$({$과 ${\displaystyle {R\mathrm{}}_{}}$ 2$({$의 차이는 $다음$과 같습니다.

${\displaystyle R_{2}-R_{1}=R{1+{\frac {x_{2}^{2}}+{\frac {y_{2}^2}}{{2}}}-R{\sqrt {1+\frac {1}^{2}}^{2}}}}-R{{{\sqrt {1}^{2}}}}^{{2}}}}}}{{{{}}}}}}}}}}}}{{{{{{{{{{1}}}}}}}}}}}}}$

${\displaystyle {그러나\mathrm{}}_{}}$ x${\displaystyle {}_{}}$1, ${\displaystyle {}_{}{}_{}{2\mathrm{}}_{}}$, ${\displaystyle {y\mathrm{}}_{}}$ 1$({$}, $x_{2}, y_{1$}) $및$ ${\displaystyle {y\mathrm{}}_{}}$ 2$({$는 모두 R$({displaystyle$ R$\})$보다 훨씬 작기 $때문$에 제곱근은 Taylor expanded일 수 있습니다.

${\displaystyle R_{2}-R_{1}=R\left(1+{\frac {1}{2}}\lefts\frac {x_{2}^{2}+y_{2}}^{2}}{R^{2}\right)-R\left(1+{\frac {1}{2}}\left({\frac {x_{1}^{2}+y_{1)}^{2}}{R^{2}}\right)\right)}$

대수적 조작을 거쳐서, 그 과정을 단순화하면

${\displaystyle R_{2}-R_{1}=flac {1}{2R}\left((x_{2}-x_{1})+(y_{2}-y_{1})(y_{2}+y_{1}\right)$

${\displaystyle {P1\mathrm{}}_{}}$${\displaystyle (}$$디스플레이$ ${\displaystyle {스타일\mathrm{}}_{}{P\_\mathrm{}}_{}}$1$}와 P2(디스플레이$ $스타일$ $P_{2$ $사이$의 $x{\displaystyle {}_{}}$$($$x_$${$1}+{$1})$ $축$을 따라 1,$$${\displaystyle \frac{2\mathrm{}}{}}$$$${\displaystyle \frac{R}{}{}_{}{}_{}}$ $디스플레이)$가 됩니다.$ystyle$ l$\}$ : 방향의 1개, 소스에 코사인 됩니다.$마찬가지$로 m ${\displaystyle =}$ ${\displaystyle \frac{1}{}}$ 2${\displaystyle \frac{}{}{}_{}}$ (${\displaystyle {}_{}{y\mathrm{}}_{}}$ 2 + ${\displaystyle {y\mathrm{}}_{}}$1 ){ $display$ $style$ m =$420$ frac ${ 2R$}($y_{2$} + $y_{1$입니다.또,$$u { $display style$u$}$는$$$P1$과$$$P_style$2 $사이$의 파장수로 정의되어 $있습니다{\displaystyle }$.

${\displaystyle u=snarfrac {2\pi c}}(x_{1}-x_{2})$

마찬가지로 v$${\$displaystyle$ v$}$는$Y축$에 따른 $(\$$displaystyle$ $P_{1})$과 $(\$$$$P_{2})$ $사이$의 파장 수이므로

$({displaystyle v=modecfrac{2\pi c}}(y_{1}-y_{2}))$

이런 이유로

$({displaystyle R_{2}-R_{1}=black {2\pi c}{\opega }}}(ul+vm)}$

${\displaystyle {x\mathrm{}}_{}}$1, ${\displaystyle {x\mathrm{}}_{}}$2, ${\displaystyle {y\mathrm{}}_{}}$1,$${\$displaystyle x_{1$}, $x_{2$}, $y_{1$} $및$ $(\$는 모두 R$(\displaystyle$R$),$ ${\displaystyle {R1\mathrm{}}_{}{}_{}}$ ${\displaystyle {R2\mathrm{}}_{}r}$R(\$displaystyle$ R_1$}\simeq$ R_${2\s$보다 훨씬 작기 $때문$에 차등 영역입니다.R ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle d}$ ${\displaystyle l}$ ${\displaystyle d}$m의 $입체{\displaystyle {}^{}}$ 각도의 요소(\$displaystyle$ R$^{2},dl,dm$ 상호 일관성 함수에 대한 우리의 표현은

$\displaystyle \Gamma _{12}(u,v,0)=\int _{\textrm {source}}I(l,m)e^{-{\frac {i\opha}{c}}{\frac {2\pi c}{\opha }}}(ul+vm)},dl,dm}$

즉,

$\displaystyle \Gamma _{12}(u,v,0)=\int _{\textrm {source}}I(l,m)e^{-2\pi i(ul+vm)}\,dl\,dm}$

하지만 이 두 적분식의 한계 한 소스의 강도 기능 이 지역에 0으로 설정된 소스의 전체 비행기 다루도록 확장할 수 있다.이런 이유로,

$\Displaystyle \Gamma _{12}(u,v,0)=\iint I(l,m)e^{-2\pi i(ul+vm)},dl,dm}$

강도 함수의 2차원 푸리에 변환.이것은 증거를 완성시켰다.

정리의 가정

그 밴 Cittert–Zernike 정리 모든 것은 대략 거의 모든 천체에 대하여 사실입니다 가정에 달려 있다.그 정리와 천체 관련시키기의 가장 중요한 가정 여기에서 논의되고 있다.

소스의 일관성이 없다

한 공간에 일관성 있는 소식통은 반 Cittert–Zernike 정리에 복종하지 않는다.이게 왜, 생각하는지 보려면 우리는 대한 largeenough이다. 우리에게 P1{\displaystyle P_{1}사이의 상호 코히 런스 함수를 계산하}와 P2{\displaystyle P_{2}자}관찰의 비행기에 있는 소스 을 두점,{\displaystyle}로 구성된{\displaystyle b}을 지킨다.중첩, P1{\displaystyle P_{1}에서의 전기장}의 원칙 출신이다.

${\displaystyle E_{1}=E_{a1}+E_{b1}}$

그리고 P2{\displaystyle P_{2}에서}이다.

${\displaystyle E_{2}=E_{a2}+E_{b2}}$

그래서 상호 코히 런스 함수이다.

${\displaystyle\langle E_{1}(t)E_ᆬ^ᆭ(t-\tau)\rangle =\langle(E_{a1}(t)+.E_ᆫ(t))(E_{a2}^{*}(t-\tau)+E_ᆬ^ᆭ(t-\tau))\rangle}$

어느 쪽이 되는가

$\displaystyle E_{1}(t)E_{2}^{*}(t-\tau)\rangle =\rangle E_{a1}(t)^{*}(t-\tau)\rangle +\rangle E_{a1}(t)E_{b2}(tau)^*}(tau)$

$점 a$와$b가$$$일관성이 있는 경우 위의 방정식의 교차항은 사라지지 않습니다.이 경우, 확장된 간섭성 선원에 대한 상호 간섭성 함수를 계산할 때, 우리는 선원의 강도 함수를 통해 간단히 통합할 수 없을 것이다. 즉, 0이 아닌 교차 항이 존재하면 상호 간섭성 함수는 단순한 형태가 아니다.

이 가정은 대부분의 천문학적 근원에 적용된다.맥동과 매이저는 일관성을 보이는 유일한 천문학적 원천이다.

소스까지의 거리

이 정리의 증명에서는 R${\displaystyle {x\mathrm{}}_{}}$x ${\displaystyle {1\mathrm{}}_{}}$ - ${\displaystyle {}_{}}$2 ({$displaystyle$ R$\gg x_{1$} - $x_{2$}}) 및$$ $R{\displaystyle {y\mathrm{}}_{}}$ y${\displaystyle {}_{}}$1 - ${\displaystyle {}_{}}$ ({$displaystyle$ R$\gg y_{1}-y_2$로 가정합니다. 즉, 소스까지의 거리가 관측 영역의 크기보다 훨씬 크다고 가정합니다.더 정확히 말하면, 반 시터트-제르니케 정리는 우리가 소위 원거리 장에서 근원을 관찰할 것을 요구한다.따라서 D$(\displaystyle$ D$)$가 관측 영역의 특성 크기(예: 2접시 전파 망원경의 경우, 두 망원경 사이의 기준선 길이)인 경우,

${\displaystyle R\gg {D^{2}}{\lambda }}$

파장 1cm의 초대형 어레이에 대해 20km의 적당한 기준선을 사용할 경우 원거리 거리는 $4{\displaystyle \mathrm{}}$× $({$ 4$\times$ 10$^{10}}$m$$)입니다.따라서 파섹보다 더 멀리 있는 천문학적 물체는 먼 장에 있습니다.그러나 태양계의 물체는 반드시 먼 곳에 있는 것은 아니기 때문에 반 시터트-제르니케 정리는 그들에게 적용되지 않는다.

소스의 각도 크기

van Cittert-Zernike 정리를 도출할 때 방향 $코사인{\displaystyle }$l {\$displaystyle$ l$}$ $및$ $m{\displaystyle \frac{\mathrm{}}{}}$ {\$displaystyle$ m${\displaystyle \}}$을 1${\displaystyle \frac{2}{}}$ (${\displaystyle {}_{}{}_{}}$+ $x2$ /$$R ($x_$${1}$ + x_{$2}) / 1$(${\displaystyle {x\_1\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {y\mathrm{}}_{}}$2 ) / ${\displaystyle \frac{1}{}}$ (${\displaystyle {}_{}}$ + 2${\displaystyle }$) / $frac$style ${\$ frac style {1} /$$ ($x2$ ) 로 $씁니다{\displaystyle \frac{\mathrm{}}{}}$., R${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{1}{}}$ ${\displaystyle {}_{}}$( ${\displaystyle {x\mathrm{}}_{}}$1 + ${\displaystyle {x\mathrm{}}_{}}$2 $){$ $displaystyle$R \$g$ { $frac${ { } {$2}}($${$$1}$ + ${\displaystyle {x\_\mathrm{}}_{}}$${2})$ $및{\displaystyle }$ R${\displaystyle \frac{1}{}}$ 1 2${\displaystyle }$( y ${\displaystyle {}_{}}$+ ${\displaystyle {}_{}}$ $){$ $displaystyle$ R$\g${ $frac$ {$1}$ {$2$$x_2)이후$ 무시된 세 번째 방향 코사인.그러나 만약 선원이 큰 각도 범위를 가지고 있다면, 우리는 이 세 번째 방향 코사인(cosine)을 무시할 수 없고, 반 시터트-제르니케 정리는 더 이상 유지되지 않는다.

대부분의 천문학적인 원천은 하늘의 매우 작은 각도(일반적으로 1도 미만)에 근접하기 때문에, 이 정리에 대한 가정은 전파 천문학 영역에서 쉽게 충족됩니다.

준단색파

반 시터트-제르니케 정리는 선원이 준단색체라고 가정한다.즉, 소스가 $평균{\displaystyle \mathrm{}}$ $주파수{\displaystyle }$ ${\$ { $displaystyle$\ $Delta$\ $nu$$}$의 범위에서 빛을 방출하는 경우, 그 소스는 다음을 충족해야 합니다.

$(\displaystyle\frac\delta\nu}{\nu}}\lesssim 1}$

또한 대역폭은 다음과 같이 좁혀야 합니다.

$(\displaystyle\frac{Delta\nu}{\nu}}\ll {frac{1}{lu}})$

$여기$서 l$\displaystyle$l은 소스 크기를$$ $나타내는{\displaystyle }$ 방향 코사인이고 u$\displaystyle$u는 조리개 한쪽 끝과$$ 다른 쪽 끝 사이의 파장 수입니다.이 전제조건이 없으면$$t\$displaystyle$와 ${\displaystyle {}_{}}$(${\displaystyle {}_{}}$ -${\displaystyle {}_{}{R\mathrm{}}_{}1}$)$$/ c\$displaystyle (R_{2}-R_{1}/c}$을$({\displaystyle }$를) 무시할 수 없습니다.

이 요건은 전파 천문학자가 대역 통과 필터를 통해 신호를 제한해야 한다는 것을 의미합니다.전파 망원경은 거의 항상 비교적 좁은 대역 통과 필터를 통해 신호를 통과시키기 때문에, 일반적으로 이러한 가정은 실제로 충족됩니다.

2차원 소스

우리는 우리의 근원이 2차원 평면에 있다고 가정한다.사실, 천문학적 근원은 3차원이다.그러나 원거리 필드이기 때문에 각 분포는 거리에 따라 변하지 않습니다.그러므로 우리가 천문원을 측정할 때, 그 3차원 구조는 2차원 평면 위에 투영된다.이것은 반 시터트-제르니케 정리가 천문원의 측정에 적용될 수 있다는 것을 의미하지만, 우리는 그러한 측정으로 시선 방향의 구조를 결정할 수 없다.

배지의 균질성

van Cittert-Zernike 정리는 선원과 영상 평면 사이의 매체가 균질하다고 가정합니다.매체가 균질하지 않으면 매체를 통과하는 빛의 이동시간의 차이로 인해 광원의 한 영역으로부터의 빛이 광원의 다른 영역에 대해 다르게 굴절된다.이종 매질의 경우 홉킨스 공식이라고 불리는 반 시터트-제르니크 정리의 일반화 방법을 사용해야 한다.

파장이 성간(은하간) 매체를 통과하여 지구 대기로 이동할 때 완전히 균일한 매체를 통과하지 않기 때문에, 반 시터트-제르니케 정리는 천문학적인 원천에 대해 정확하게 성립하지 않습니다.그러나 실제로는 성간 및 은하간 매체와 지구 대기의 굴절률의 변화는 이 정리가 합리적인 실험 오차 내에서 거의 진실일 정도로 충분히 작습니다.매체의 굴절률의 이러한 변화는 균질 매체를 통과하는 파면의 경우 약간의 섭동을 야기할 뿐이다.

홉킨스 공식

매체가 현재 이질적이라는 점을 제외하고 판 시터트-제르니케 정리가 도출되었을 때와 동일한 상황이 발생했다고 가정합니다.${\displaystyle \mathrm{따라서}}$ 미디어 $K{\displaystyle }$( l${\displaystyle }$,${\displaystyle m}$ ,${\displaystyle P}$ , ${\displaystyle )}$ $){$ $display K ( l$ ,$m$ , $P$, \ $nu$의 전송 함수를 소개합니다.앞과 유사한 파생 결과를 보면,

$\Displaystyle \Gamma _{12}(l,m,0)=\gamda ^{2}\iint I(l,m)K(l,m,P_{1},\nu)K^{*}(l,m,P_{2},\nu),D},S}$

정의하면

$\displaystyle U(l,m,P_{1}\equiv i\lambda K(l,m,P_{1},\nu){\sqrt {I(l,m)}}$

그러면 상호 일관성 함수는

$\displaystyle \Gamma _{12}(l,m,0)=\int U(l,m,P_{1})U^{*}(l,m,P_{2}),dS}$

홉킨스의 반 시터트-제르니케 ^[5]정리 일반화입니다.동종 매체의 특수한 경우, 전송 기능은

${\displaystyle K(l,m,P,\nu)=-{\frac {ie^{ikR}}{\lambda R}}$

이 경우 상호 일관성 함수는 소스의 밝기 분포의 푸리에 변환으로 감소합니다.홉킨스 공식의 주요 장점은 밝기 분포를 측정하여 선원의 상호 일관성 함수를 간접적으로 계산할 수 있다는 것이다.

정리의 응용

조리개 합성

반 시터트-제르니케 정리는 선원의 밝기 분포 측정에 매우 중요합니다.두 개의 망원경을 사용하여 전파 천문학자(또는 적외선 또는 밀리미터 이하의 천문학자)는 소스로부터의 어떤 점 때문에 두 접시에서 전기장 사이의 상관관계를 측정할 수 있습니다.이 상관관계를 선원의 여러 점에 대해 측정함으로써 천문학자들은 선원의 가시성 함수를 재구성할 수 있다.반 시터트-제르니케 정리를 적용함으로써 천문학자들은 가시성 함수의 역 푸리에 변환을 취하여 광원의 밝기 분포를 발견할 수 있다.이 기술은 조리개 합성 또는 합성 이미징으로 알려져 있습니다.

실제로 전파천문학자들은 측정된 가시성 함수의 역 푸리에 변환을 직접 취함으로써 광원의 밝기 분포를 거의 회복하지 못한다.이러한 과정은 나이키스트 표본 추출 정리를 만족시키기 위해 충분한 수의 샘플이 필요합니다. 이는 선원의 밝기 분포를 대략적으로 재구성하는 데 필요한 것보다 훨씬 더 많은 관측치입니다.따라서 천문학자들은 천문원의 밝기 분포에 대한 물리적 제약을 이용하여 관측해야 하는 횟수를 줄입니다.밝기 분포는 어디에서나 실재하고 양의 값이어야 하므로 가시성 함수는 샘플링되지 않은 영역에서 임의의 값을 취할 수 없습니다.따라서 CLEAN 또는 Maximum Entropo와 같은 비선형 디콘볼루션 알고리즘을 사용하여 제한된 수의 ^[6]관측치로부터 선원의 밝기 분포를 대략적으로 재구성할 수 있습니다.

적응광학

반 시터트-제르니케 정리도 적응광학계의 감도에 제약을 가한다.적응광학(AO) 시스템에서는 왜곡된 파면이 제공되므로 왜곡이 없는 파면으로 변환해야 합니다.AO 시스템은 파형 전면에서 왜곡을 제거하기 위해 여러 가지 다른 수정을 수행해야 합니다.이러한 보정 중 하나는 파면을 두 개의 동일한 파면으로 분할하고 파면 평면에서 물리적 $거리{\displaystyle }$ s$(\displaystyle$ s$)$만큼$$ 이동하는 것입니다.그런 다음 두 개의 웨이브프론이 겹쳐져 프린지 패턴을 만듭니다.AO 시스템은 테두리의 크기와 간격을 측정함으로써 ^[7]파면을 따라 위상차를 결정할 수 있습니다.이 기술은 "전단"으로 알려져 있습니다.

이 기술의 감도는 반 시터트-제르니케 ^[8]정리에 의해 제한된다.확장된 선원을 촬상하면 선원의 ^[9]휘도 분포의 푸리에 변환에 비례하는 계수만큼 선단 사이의 콘트라스트가 감소한다.반 시터트-제르니케 정리는 AO 시스템에 의해 촬영된 확장된 선원의 상호 일관성이 밝기 분포의 푸리에 변환이 될 것임을 암시합니다.따라서 확장된 선원은 가장자리들의 상호 일관성을 변화시켜 대비를 감소시킵니다.

자유 전자 레이저

반 시터트-제르니케 정리는 자유 전자 레이저로부터 방사선의 부분 공간적 일관성을 계산하기 위해 사용될 수 있다.

「 」를 참조해 주세요.

• 일관성 정도
• 일관성 이론
• 가시성
• Hanbury Brown and Twiss 효과
• 보스-아인슈타인 상관 관계

레퍼런스

참고 문헌

• M. & Wolf, E. 출생: Pergamon Press, Oxford, 1987, 510 페이지
• Klein, Miles V. & Furtak, Thomas E:광학, John Wiley & Sons(뉴욕), 1986년 제2판, 544-545페이지

외부 링크

• 응용 프로그램을 사용하여 Van Cittert-Zernike-theem에 대해 강의합니다. 버클리 대학입니다, 교수님. 데이비드 T. Attwood on YouTube (AST 210/EE 213 강의 23)]