네트워크 관리 기능

단순한 네트워크 제어

네트워크 제어성은 네트워크의 구조적 제어성에 관한 것입니다.제어성은 입력의 적절한 선택과 함께 모든 초기 상태에서 원하는 최종 상태로 동적 시스템을 안내하는 능력을 나타냅니다.이 정의는 통제에 대한 우리의 직관적인 개념과 잘 일치합니다.일반적인 다이렉트 및 가중 복합 네트워크의 제어 가능성은 최근 전 세계 다양한 네트워크의 많은 그룹에서 집중적으로 연구되고 있습니다.다형 생물학적 네트워크(유전자, miRNA 유전자, 단백질-단백질 상호작용 네트워크)에 대한 샤르마 외 ^[1]연구진의 최근 연구는 종양 미세 환경 유지를 담당하는 유전자와 단백질의 중요한 역할을 보여주는 표현형 특성화된 골육종에서 대조군 대상을 식별했다.

배경

복잡한 ${\dot {\mathbf {X} }}(t)=\mathbf {A} \cdot \mathbf {X} (t)+\mathbf {B} \cdot \mathbf {u} (t)$ 표준 선형 시공간역학 X ${\dot {\mathbf {X} }}(t)=\mathbf {A} \cdot \mathbf {X} (t)+\mathbf {B} \cdot \mathbf {u} (t)$ ( ${\dot {\mathbf {X} }}(t)=\mathbf {A} \cdot \mathbf {X} (t)+\mathbf {B} \cdot \mathbf {u} (t)$ ) ${\dot {\mathbf {X} }}(t)=\mathbf {A} \cdot \mathbf {X} (t)+\mathbf {B} \cdot \mathbf {u} (t)$ ${\dot {\mathbf {X} }}(t)=\mathbf {A} \cdot \mathbf {X} (t)+\mathbf {B} \cdot \mathbf {u} (t)$ X ( ${\dot {\mathbf {X} }}(t)=\mathbf {A} \cdot \mathbf {X} (t)+\mathbf {B} \cdot \mathbf {u} (t)$ ) + ${\dot {\mathbf {X} }}(t)=\mathbf {A} \cdot \mathbf {X} (t)+\mathbf {B} \cdot \mathbf {u} (t)$ ${\dot {\mathbf {X} }}(t)=\mathbf {A} \cdot \mathbf {X} (t)+\mathbf {B} \cdot \mathbf {u} (t)$ ( ${\dot {\mathbf {X} }}(t)=\mathbf {A} \cdot \mathbf {X} (t)+\mathbf {B} \cdot \mathbf {u} (t)$ ){ $display$ { $dot$ \ dot \ $mathbf$ { $X$ } $=$ \ $mathbf$ { $A }$ \ $cdot$ \ $mathbf { X$ } ( $t$ ) = \ mathbf { X } ( t ) \ $cdot$ } \ $mathbf$ { \ $mathbf$ { \ cdot $}$ \ mathbf { \ cdot } \ cdot } \ mathbf { \ cdot } \ m ${X}(t)=(x_{1}(t),\cdots,x_{N}(t))$ $^{\mathrm {T}}:$ N 노드 $\mathbf {X} (t)=(x_{1}(t),\cdots ,x_{N}(t))^{\mathrm {T} }$ $(\displaystyle$ N $t$ 의 $N$ $시스템$ 상태를 $시각$ t ${displaystyle$ t $}$ 에 캡처합니다.N $N\times N$ × $($ 디스플레이 $스타일$ N $\times$ N $)$ $\mathbf {A}$ A $($ 스타일 $\mathbf {A})$ 는 $\mathbf {A}$ 시스템의 배선 다이어그램과 구성 요소 간의 상호 작용 강도를 나타냅니다.N $N\times M$ × $(\displaystyle$ N $\times$ M $)$ $\mathbf {B}$ B(\ $displaystyle \mathbf {B})$ 는 $N\times M$ 외부 컨트롤러에 의해 제어되는 노드를 나타냅니다 $\mathbf {B}$ .시스템은 시간 의존 입력 $\mathbf {u} (t)=(u_{1}(t),\cdots ,u_{M}(t))^{\mathrm {T} }$ u ( $\mathbf {u} (t)=(u_{1}(t),\cdots ,u_{M}(t))^{\mathrm {T} }$ ) $=$ ( $\mathbf {u} (t)=(u_{1}(t),\cdots ,u_{M}(t))^{\mathrm {T} }$ 1 ( $\mathbf {u} (t)=(u_{1}(t),\cdots ,u_{M}(t))^{\mathrm {T} }$ ) , $\mathbf {u} (t)=(u_{1}(t),\cdots ,u_{M}(t))^{\mathrm {T} }$ , $\mathbf {u} (t)=(u_{1}(t),\cdots ,u_{M}(t))^{\mathrm {T} }$ M ( $\mathbf {u} (t)=(u_{1}(t),\cdots ,u_{M}(t))^{\mathrm {T} }$ ) T $\mathbf {u} (t)=(u_{1}(t),\cdots ,u_{M}(t))^{\mathrm {T} }$ { $displaystyle \mathbf$ { $u} ($ t )=( $u_{1}(t),\cdots,u_{M}(t))$ 를 통해 제어됩니다.컨트롤러가 시스템에 $강제하는 ^{\mathrm$ {T $}}}.$ 제어가 시스템의 역학을 완전히 제어하기에 충분한 N $(\$ 로 표시된 드라이버 노드의 최소 수를 식별하기 위해 Liu ^[2]등은 구조 제어 이론, 그래프 이론 및 통계 물리학에서 도구를 결합하려고 시도했습니다.네트워크의^[2] 완전한 제어를 유지하기 위해 필요한 최소 입력 또는 드라이버 노드 수는 네트워크의 '최대 일치' 즉, 시작 노드 또는 끝 노드를 공유하지 않는 링크의 최대 세트에 의해 결정된다는 것을 알 수 있었습니다.이 결과로부터 인아웃 도 분포에 기초한 분석 프레임워크가 개발되었으며, 스케일 프리 및 Erdgs-Rény ^[2]그래프에 대해 n $n_{\mathrm {D} }=N_{\mathrm {D} }/N$ $= N$ D / $n_{\mathrm {D} }=N_{\mathrm {D} }/N$ $(\displaystyle$ n_ ${\mathrm {D} }/N})$ 을 $n_{\mathrm {D} }=N_{\mathrm {D} }/N$ $n_{\mathrm {D} }=N_{\mathrm {D} }/N$ 했다.그러나 최근에는 네트워크 제어성(및 기본 다이내믹스를 단순화하기 위해 그래프의 $\mathbf {A}$ 만을 사용하는 기타 구조 전용 방법 $(\$ 이 모두 언더슈팅과 오버슈트 양쪽에 있으며, 어떤 드라이버 노드가 네트워크 다이내믹스를 가장 잘 제어하는지, 높은 것으로 입증되었습니다.제어 ^[3]결정 시 중복성(예: 운하화) 및 비선형 역학의 중요성을 조명한다.

또한 Liu 등의 공식은^[2] 체인 그래프와 약한 밀도로 연결된 그래프에 대해 $({$ 의 ${n_{\mathrm {D} }}$ ${n_{\mathrm {D} }}$ 한 값을 예측한다는 점도 주목할 만하다.두 그래프 모두 차수 분포와 차수 분포가 매우 다릅니다.최근 ^[4]발표되지 않은 연구에서는 네트워크에서의 순수 로컬 측정치인 정도가 완전히 제어 가능성을 나타내는지 여부 및 약간 떨어진 노드도 네트워크 제어 가능성을 결정하는 데 아무런 역할을 하지 않는지에 대해 의문을 제기하고 있습니다.실제로 많은 실제 단어 네트워크, 즉 먹이 웹, 신경 및 대사 네트워크의 경우 n ${n_{\mathrm {D} }}^{real}$ $e$ { $n_{\mathrm$ { $D}^{$ real ${n_{\mathrm {D} }}^{real}$ }} ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${\$ { $n_{\mathrm$ {D $}}}}$ 의 ${n_{\mathrm {D} }}^{real}$ 의 불일치는 Liu에 의해 계산되었다 ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ $.$ 제어성이 주로 정도에 따라 결정되는 경우 n ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{real}$ 는 ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ l ${n_{\mathrm {D} }}^{real}$ { $n_{\mathrm {D}}{$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ $}}{$ $displaystyle {n_{\mathrm {D}}}{\mathrm {rand\$ a n ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ }}}}{d}}}}}}{ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ a n ${n_{\mathrm {D} }}^{real}$ styledisplaystyle이들은 (arXiv:1203.5161v1) 이것이 정도 상관의 효과 때문일 수 있다고 주장했다.단, 네트워크 제어성은 정도(그래프 이론)나 정도 상관관계를 전혀 사용하지 않고, 사이의 중심성과 근접성 중심성을 사용하는 것만으로 변경할 수 있는 것으로 나타났습니다^[4].

개략도는 다이렉트 네트워크의 제어를 나타내고 있습니다.주어진 다이렉트 네트워크(그림 a)의 경우 최대 일치를 계산한다. 즉, 공통 헤드 또는 테일이 없는 가장 큰 에지 세트이다.최대 매칭은 정점 분리 방향 경로와 방향 주기의 집합으로 구성된다(그림.b의 빨간색 가장자리 참조).노드가 일치하는 에지의 선두일 경우 해당 노드가 일치합니다(그림.b의 녹색 노드).그렇지 않으면 일치하지 않습니다(그림.b의 흰색 노드).이러한 일치하지 않는 노드가 제어해야 하는 노드(드라이버 노드)입니다.이러한 드라이버 노드에 신호를 주입함으로써 시작점을 입력으로 하는 일련의 유도 경로를 얻을 수 있습니다(그림 c 참조).이러한 경로를 "줄기"라고 합니다.이 그래프는 U-root 요인 연결이라고 합니다.지시된 사이클을 이러한 "줄기"에 "기여"함으로써 "버드"를 얻을 수 있습니다.이 그래프는 선인장이라고 불린다(그림 d 참조).구조제어성 ^[5]정리에 따르면 제어된 네트워크를 가로지르는 선인장 구조가 존재하므로(그림 e 참조) 시스템을 제어할 수 있다.제어 네트워크의 기초가 되는 선인장 구조(그림 d)는 제어성을 유지하기 위한 "스켈톤"이다.

구조 제어 기능

구조 특성의 개념은 Lin(1974년)^[5]에 의해 처음 도입되었고, Shields와 Pearson(1976년)^[6]에 의해 확장되었으며, Glover와 Silverman(1976년)^[7]에 의해 대체적으로 도출되었다.주요 질문은 가변 시스템 매개변수와 관련하여 제어 가능성 또는 관측 가능성의 결여가 일반적이냐는 것입니다.구조 제어 프레임워크에서 시스템 매개변수는 독립 자유 변수 또는 고정 0입니다.이는 파라미터 값이 정확하게 알려져 있지 않기 때문에 물리 시스템의 모델에 대해 일관성이 있습니다.단, 상호작용 또는 접속의 부재를 나타내는 제로 값은 예외입니다.

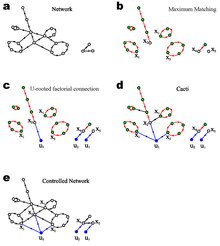
최대 일치

그래프 이론에서 매칭은 공통 정점이 없는 가장자리 집합입니다.류 ^[2]외이 정의를 방향 그래프로 확장했습니다.여기서 매칭은 시작 정점 또는 끝 정점을 공유하지 않는 방향 에지 세트입니다.방향 그래프의 매칭이 정점-분리 단순 경로 및 사이클 집합으로 구성되어 있는지 쉽게 확인할 수 있습니다.다이렉트 네트워크의 최대 매칭은 최악의 경우 O(E'N) 시간으로 실행되는 고전적인 Hopcroft-Karp 알고리즘을 사용하여 초당 표현으로 효율적으로 계산할 수 있습니다.무방향 그래프의 경우,^[8] 통계물리학에서 개발된 캐비티 방법을 사용하여 최대 매칭의 크기와 수에 대한 분석 솔루션을 연구하였다.류 ^[2]외방향 그래프의 계산을 확장했습니다.

Liu ^[2]등은 광범위한 실제 네트워크의 최대 일치를 계산함으로써 드라이버 노드의 수는 주로 $P(k_{\mathrm {in} },k_{\mathrm {out} })$ $P(k_{\mathrm {in} },k_{\mathrm {out} })$ P $P(k_{\mathrm {in} },k_{\mathrm {out} })$ n, k $o$ $P(k_{\mathrm {in} },k_{\mathrm {out} })$ t $)$ ${displaystyle$ P( $k_{\$ mathrm { $in}},k_{\mathrm$ { $out$ 에 의해 결정된다고 주장했다.그들은 또한 캐비티 방법을 사용하여 임의의 정도 분포를 갖는 네트워크 앙상블의 평균 드라이버 노드 수를 계산했다.그것은 체인 그래프와 약한 조밀하게 연결되어 그래프, 둘 다 매우 정도 분포와 안팎에서 달라요;류(알의 공식이 흥미롭다.[2]}}}. 또한, 많은 real-word 네트워크, 즉 먹이 사슬,과 신진 대사인 신경 네트워크에 대한, t. nD{\displaystyle{n_{\mathrm{D}의 동일한 가치를 예측하는 것이다그는 Liu ^[2]등이 계산한 ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ n ${n_{\mathrm {D} }}^{real}$ ${n_{\mathrm {D} }}^{real}$ $({$ 와 ${n_{\mathrm {D} }}^{real}$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ({ $displaystyle {n_{\mathrm {D}}})$ 의 ${n_{\mathrm {D} }}^{real}$ 이 일치하지 않는다.제어성이 순전히 정도에 따라 결정되는 경우 ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{real}$ 는 ${n_{\mathrm {D} }}^{real}$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${\$ ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ $}}{$ $displaystyle {n_{\mathrm {D}}}}}}{\mathrm$ { $\del$ 의 실제 네트워크에서는 왜 ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ${n_{\mathrm {D} }}^{real}$ 가 ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ ?네트워크에서의 제어 견고성이 정도(그래프 이론) 기반의 메트릭을 사용하여 중심성 및 근접성^[4] 중심성에 더 큰 영향을 미치는지는 여전히 정밀하게 조사됩니다.

희소 그래프는 ^[2]^[4]제어하기가 더 어렵지만, 간성 중심과 근접성 중심^[4] 또는 정도 이질성이^[2] 거의 유사한 정도 분포를 가진 희소 그래프의 제어 가능성을 결정하는 데 더 중요한 역할을 하는지 확인하는 것은 분명 흥미로울 것이다.

복합 양자계와 대수 그래프 이론의 제어

네트워크의 제어 이론은 또한 복합 양자 시스템을 위한 범용 제어의 맥락에서 개발되었으며, 여기서 서브시스템과 그 상호작용은 각각 ^[9]노드와 링크와 관련된다.이 프레임워크는 그래프의 최소 순위와 관련 개념을 통해 대수 그래프 이론에서 ^[10]^[11]도구를 사용하여 칼만의 기준을 공식화할 수 있도록 한다.

「」를 참조해 주세요.

제어성 Gramian

레퍼런스

^ Sharma, Ankush; Cinti, Caterina; Capobianco, Enrico (2017). "Multitype Network-Guided Target Controllability in Phenotypically Characterized Osteosarcoma: Role of Tumor Microenvironment". Frontiers in Immunology. 8: 918. doi:10.3389/fimmu.2017.00918. ISSN 1664-3224. PMC 5536125. PMID 28824643.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m Liu, Yang-Yu; Slotine, Jean-Jacques; Barabási, Albert-László (2011). "Controllability of complex networks". Nature. Springer Science and Business Media LLC. 473 (7346): 167–173. Bibcode:2011Natur.473..167L. doi:10.1038/nature10011. ISSN 0028-0836. PMID 21562557. S2CID 4334171.
^ Gates, Alexander J.; Rocha, Luis M. (2016-04-18). "Control of complex networks requires both structure and dynamics". Scientific Reports. Springer Science and Business Media LLC. 6 (1): 24456. arXiv:1509.08409. Bibcode:2016NatSR...624456G. doi:10.1038/srep24456. ISSN 2045-2322. PMC 4834509. PMID 27087469.
^ ^a ^b ^c ^d ^e Banerjee, SJ; Roy, S (2012). "Key to Network Controllability". arXiv:1209.3737 [physics.soc-ph].
^ ^a ^b C.-T. Lin, IEEE 트랜스 Auto. Contr. 19(1974년)
^ R. W. Shields 및 J. B. Pearson, IEEE Trans. 자동. Contr. 21(1976년)
^ K. Glover와 L. M. Silverman, IEEE 트랜스 자동. Contr. 21(1976년)
^ L. 즈데보로바와 M. 메자드, J. Stat. Mech. 05 (2006)
^ Burgarth, Daniel; Giovannetti, Vittorio (2007-09-05). "Full Control by Locally Induced Relaxation". Physical Review Letters. 99 (10): 100501. arXiv:0704.3027. Bibcode:2007PhRvL..99j0501B. doi:10.1103/physrevlett.99.100501. ISSN 0031-9007. PMID 17930379. S2CID 6560929.
^ Burgarth, Daniel; D'Alessandro, Domenico; Hogben, Leslie; Severini, Simone; Young, Michael (2013). "Zero forcing, linear and quantum controllability for systems evolving on networks". IEEE Transactions on Automatic Control. 58 (9): 2349–2354. doi:10.1109/TAC.2013.2250075. MR 3101617. S2CID 6939245.
^ S. O'Rourke, B.투리, https://arxiv.org/abs/1511.05080.

외부 링크

[1] Sharma, Ankush; Cinti, Caterina; Capobianco, Enrico (2017). "Multitype Network-Guided Target Controllability in Phenotypically Characterized Osteosarcoma: Role of Tumor Microenvironment". Frontiers in Immunology. 8: 918. doi:10.3389/fimmu.2017.00918. ISSN 1664-3224. PMC 5536125. PMID 28824643.

[Liu-Nature-11-2] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m Liu, Yang-Yu; Slotine, Jean-Jacques; Barabási, Albert-László (2011). "Controllability of complex networks". Nature. Springer Science and Business Media LLC. 473 (7346): 167–173. Bibcode:2011Natur.473..167L. doi:10.1038/nature10011. ISSN 0028-0836. PMID 21562557. S2CID 4334171.

[gates_rocha_scirep-3] Gates, Alexander J.; Rocha, Luis M. (2016-04-18). "Control of complex networks requires both structure and dynamics". Scientific Reports. Springer Science and Business Media LLC. 6 (1): 24456. arXiv:1509.08409. Bibcode:2016NatSR...624456G. doi:10.1038/srep24456. ISSN 2045-2322. PMC 4834509. PMID 27087469.

[Arxiv_Close_Betw-4] Banerjee, SJ; Roy, S (2012). "Key to Network Controllability". arXiv:1209.3737 [physics.soc-ph].

[Lin-74-5] C.-T. Lin, IEEE 트랜스 Auto. Contr. 19(1974년)

[Shields-76-6] R. W. Shields 및 J. B. Pearson, IEEE Trans. 자동. Contr. 21(1976년)

[Glover-76-7] K. Glover와 L. M. Silverman, IEEE 트랜스 자동. Contr. 21(1976년)

[Zdeborova-06-8] L. 즈데보로바와 M. 메자드, J. Stat. Mech. 05 (2006)

[BG-07-9] Burgarth, Daniel; Giovannetti, Vittorio (2007-09-05). "Full Control by Locally Induced Relaxation". Physical Review Letters. 99 (10): 100501. arXiv:0704.3027. Bibcode:2007PhRvL..99j0501B. doi:10.1103/physrevlett.99.100501. ISSN 0031-9007. PMID 17930379. S2CID 6560929.

[BDHSY-13-10] Burgarth, Daniel; D'Alessandro, Domenico; Hogben, Leslie; Severini, Simone; Young, Michael (2013). "Zero forcing, linear and quantum controllability for systems evolving on networks". IEEE Transactions on Automatic Control. 58 (9): 2349–2354. doi:10.1109/TAC.2013.2250075. MR 3101617. S2CID 6939245.

[OT-15-11] S. O'Rourke, B.투리, https://arxiv.org/abs/1511.05080.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

Search

네트워크 관리 기능

네임스페이스

더

목차

배경

구조 제어 기능

최대 일치

복합 양자계와 대수 그래프 이론의 제어

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

네트워크 관리 기능

배경

구조 제어 기능

최대 일치

복합 양자계와 대수 그래프 이론의 제어

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.