검색 및 최적화 시 무료 점심식사 없음
No free lunch in search and optimization계산 복잡성과 최적화에서 무료 점심식사 없는 정리는 특정 유형의 수학 문제의 경우, 클래스 내 모든 문제에 대해 평균적으로 해결책을 찾는 계산 비용이 어떠한 해결 방법에서도 동일하다는 것을 명시하는 결과물이다. 따라서 어떤 해결책도 "짧은 컷"을 제공하지 않는다. 이는 검색 공간이 확률밀도함수라는 가정 하에 이루어진다. 무작위 검색보다 더 효율적으로 이용할 수 있는 기초 구조(예: 뉴턴의 최적화 방법)나 아예 검색 없이 결정할 수 있는 폐쇄형(예: 2차 다항식의 극치)를 가진 검색 공간에는 적용되지 않는다. 그러한 확률론적 가정에서는 특정 유형의 문제를 해결하는 모든 절차의 산출물이 통계적으로 동일하다. 데이비드[1] 월퍼트와 윌리엄 G. 맥레디가 검색과 최적화의 문제와 관련하여 소개한 그러한 상황을 다채롭게 묘사하는 방법은 공짜 점심은 없다고 말하는 것이다.[2] Wolpert는 이전에 머신러닝(통계학적 추론)[3]을 위한 무료 점심식사 이론을 도출하지 못했다. 월퍼트의 기사가 발표되기 전에 컬렌 샤퍼는 월퍼트의 이론 중 한 가지에 대한 제한된 버전을 독립적으로 증명하여 그것을 유도 문제에 대한 기계 학습 연구의 현재 상태를 비평하는 데 사용했다.[4]
'무료급식' 은유에서 각각의 '레스토랑'(문제해결 절차)은 '런치 플레이트'(문제해결 절차)와 '가격'(문제해결 절차 수행)을 연관시킨 '메뉴'가 있다. 레스토랑의 메뉴는 한 가지 점을 제외하고는 동일하다. 즉, 가격은 한 레스토랑에서 다음 레스토랑으로 옮겨진다. 각 접시를 주문할 가능성이 높은 잡식성 식당의 경우 평균 점심 비용은 식당 선택에 따라 달라지지 않는다. 그러나 경제를 추구하는 육식동물과 함께 정기적으로 점심을 먹으러 가는 채식주의자는 점심에 평균적인 비용을 지불할 수도 있다. 평균 비용을 체계적으로 줄이려면 a) 무엇을 주문할 것인지, b) 여러 식당에서 주문할 것인지에 대한 사전 지식을 활용해야 한다. 즉, 문제 해결의 성능 향상은 절차와 문제를 일치시키기 위해 사전 정보를 사용하는 것에 달려 있다.[2][4]
공식적으로는 문제 해결사가 동일한 결과를 얻을 수 있는 문제 사례에 대한 확률 분포일 때 무료 점심식사는 없다. 검색의 경우 문제 인스턴스는 객관적 함수로서, 결과는 함수 영역의 후보 해법 평가에서 얻은 값의 순서다. 결과의 일반적인 해석의 경우, 검색은 최적화 과정이다. 후보 해법 공간의 순열화 하에서 객관적 기능에 대한 분포가 불변하는 경우에만 검색 시 무료 점심식사가 없다.[5][6][7] 이 조건은 실제로 정확히 유지되지는 않지만 (거의) 무료 점심식사는 없다"는 정리는 대략 유지되고 있음을 시사한다.[6][8]
개요
일부 계산 문제는 후보 해결책의 공간에서 좋은 해결책을 찾음으로써 해결된다. 평가를 위해 후보 솔루션을 반복적으로 선택하는 방법을 검색 알고리즘이라고 한다. 특정 문제에 대해서는 서로 다른 검색 알고리즘이 다른 결과를 얻을 수 있지만, 모든 문제에 대해서는 구별할 수 없다. 알고리즘이 어떤 문제에서 우수한 결과를 얻으면 다른 문제에서 열등감을 가지고 대가를 치러야 한다는 것을 따른다. 이런 의미에서 무상급식은 찾아볼 수 없다.[1] 또는 쉐퍼에 이어 검색 성능이 보존된다.[4] 보통 검색은 최적화로 해석되는데, 이는 최적화에 공짜 점심은 없다는 관측을 낳는다.[2]
월퍼트와 맥프레디 자신이 평이한 언어로 기술한 "월퍼트와 맥프레디의 '무료 점심식사 없음' 정리"는 "어떤 두 개의 알고리즘이라도 가능한 모든 문제에 걸쳐 성능을 평균할 때 동등하다"[9]는 것이다. "무료 점심식사 없음" 결과는 문제에 대한 알고리즘을 일치시키는 것이 모두에게 고정 알고리즘을 적용하는 것보다 더 높은 평균 성능을 제공한다는 것을 나타낸다.[citation needed] Igel과 Toussaint[6], English는[7] 무료 급식이 없다는 일반적인 조건을 확립했다. 신체적으로는 가능하지만 정확하게는 유지되지 않는다.[6] 드로스테, 얀센, 웨게너는 그들이 해석하는 정리를 실전에 (거의) 공짜 점심은 없다는 것을 나타낸다.[8]
문제를 보다 구체적으로 설명하려면 문제에 직면한 최적화 실무자를 고려하십시오. 문제가 어떻게 발생했는지에 대한 어느 정도 지식을 감안할 때, 실무자는 문제를 해결하는 데 잘 수행될 알고리즘의 선택에서 지식을 활용할 수 있을 것이다. 만약 시술자가 지식을 활용하는 방법을 이해하지 못하거나 단순히 지식이 없다면, 어떤 알고리즘이 실제 문제에서 일반적으로 다른 알고리즘을 능가하는지에 대한 문제에 직면하게 된다. (거의) 무료 점심식사 금지' 정리의 저자들은 답은 본질적으로 '아니오'라고 말하지만, 그 정리가 실천을 다루는지 여부에 대해서는 약간의 유보성을 인정한다.[8]
정리
"문제"는 보다 공식적으로 후보 해결책을 선량 가치와 연관시키는 객관적 기능이다. 검색 알고리즘은 객관적 기능을 입력으로 삼고 후보 솔루션을 하나씩 평가한다. 알고리즘의 출력은 관측된 선량 값의 시퀀스다.[10][11]
Wolpert와 Macready는 알고리즘은 결코 후보 솔루션을 재평가하지 않으며 알고리즘 성능이 출력에서 측정된다고 규정한다.[2] 단순성을 위해 알고리즘의 무작위성을 허용하지 않는다. 이러한 조건에서 검색 알고리즘이 가능한 모든 입력에서 실행될 때, 그것은 각각의 가능한 출력을 정확히 한 번 생성한다.[7] 성능을 출력에서 측정하기 때문에 알고리즘은 특정 수준의 성능을 얼마나 자주 달성하는지 구별할 수 없다.
일부 성능 측정은 목표 함수의 최적화에 있어 검색 알고리즘이 얼마나 잘 수행되는지 나타낸다. 실제로, 검토 중인 클래스에는 최적화 문제 외에 흥미로운 검색 알고리즘 적용이 없는 것 같다. 공통 성능 측정치는 출력 시퀀스에서 최소값의 최소 지수다. 객관적 기능을 최소화하는 데 필요한 평가 수입니다. 일부 알고리즘의 경우 최소값을 찾는 데 걸리는 시간은 평가 횟수에 비례한다.[7]
원래의 무료 점심식사 금지(NFL) 이론은 모든 객관적 기능이 동일한 검색 알고리즘에 입력될 가능성이 있다고 가정한다.[2] 느슨하게 말하면, "흔들림" 목적 함수가 그들의 확률에 영향을 미치지 않는 경우에만 NFL이 존재한다는 것이 그 이후 확립되었다.[6][7] NFL에 대한 이러한 조건은 물리적으로 가능하지만, 확실히 정확하게 유지되지는 않는다는 주장이 제기되었다.[6]
'NFL이 아니다'라는 뻔한 해석은 '무료급식'이지만 이는 오해를 불러일으킨다. NFL은 정도 문제지, 전부 또는 아무것도 아닌 제안이 아니다. NFL 조건이 대략적으로 유지된다면, 모든 알고리즘은 모든 목표 기능에 대해 대략 동일한 결과를 산출한다.[7] "NFL이 아님"은 알고리즘이 일부 성과 측정에 의해 전체적으로 불평등하다는 것을 의미한다. 관심 성능 측정의 경우 알고리즘은 거의 동일하게 유지되거나 거의 동일하게 유지될 수 있다.[7]
콜모고로프 무작위성
가능한 모든 기능 집합의 거의 모든 요소들("기능"의 설정-이론적 의미에서)은 Kolmogorov 랜덤이며, 따라서 NFL 이론은 거의 모든 기능 집합에 적용되며, 이 기능 집합은 검색 공간의 각 포인트에 대해 구별되는 (그리고 무작위적인) 엔트리를 포함하는 룩업 테이블보다 더 압축적으로 표현할 수 없다. 좀 더 간결하게 표현할 수 있는 함수(예를 들어, 합리적인 크기의 수학적 표현에 의해)는 정의로 콜모고로프 무작위가 아니다.
또한, 가능한 모든 객관적 기능의 집합 내에서, 선의 수준은 후보 해법들 사이에서 동등하게 표현되기 때문에, 좋은 해법은 후보 영역 전체에 흩어져 있다. 따라서, 검색 알고리즘은 매우 좋은 해결책을 찾기 전에 후보자들의 소수 이상을 평가하는 일은 거의 없을 것이다.[11]
거의 모든 객관적 기능은 Kolmogorov 복잡성이 너무 높아 특정 컴퓨터에 저장할 수 없다.[5][7][11] 더 정확히 말하면, 만약 우리가 현대 컴퓨터의 기억의 순서에 따라 주어진 크기의 메모리를 가진 등록기로서 주어진 물리적 컴퓨터를 모델링한다면, 대부분의 객관적인 기능은 그들의 기억 속에 저장될 수 없다. 세스 로이드가 관측 가능한 우주가 등록할 수 있다고 추정하는 것보다 전형적인 목적 함수나 알고리즘에는 더 많은 정보가 있다.[12] 예를 들어 각 후보 해법이 300 0과 1의 순서로 인코딩되고 선량 값이 0과 1이면 대부분의 객관적 함수는 최소 2비트의300 Kolmogorov 복잡성을 가지며 이는 로이드의 1090㎛ 2비트의299 경계보다 크다.[13] 원래의 "무료 점심식사 없음" 정리가 물리적 컴퓨터에 저장될 수 있는 것에는 적용되지 않고, 그 대신에 "긴축된" 소위 "무료 점심식사" 정리는 적용할 필요가 없다는 것이다. NFL 결과는 불입력 기능에도 적용되는 것으로 나타났다.[14]
형식 시놉시스
Y는 모든 객관적 함수 f:X→Y의 집합이며, 여기서 은 유한한 솔루션 공간이고 Y Y은 포셋이다. The set of all permutations of X is J. A random variable F is distributed on . For all j in J, F o j is a random variable distributed on , with P(F o j = f) = P(F = f o j−1) for all f in .
a(f)가 입력 f의 검색 알고리즘 a의 출력을 나타내도록 한다. 모든 검색 알고리즘 a와 b에 대해 a(F)와 b(F)가 동일하게 분포된 경우, F는 NFL 분포를 가진다. 이 조건은 F와 F o j가 J의 모든 J에 대해 동일하게 분포된 경우에만 유지된다.[6][7] 즉, 솔루션 공간의 순열화 하에서 객관적 기능의 분배가 불변하는 경우에만 검색 알고리즘을 위한 무료 점심식사가 없다는 것이다.[15] 이론적 NFL 이론은 최근 임의 카디널리티 Y 로 일반화되었다[16]
기원
Wolpert와 Macready는 두 가지 주요 NFL 이론, 첫 번째는 검색이 진행되는 동안 변하지 않는 객관적 기능에 관한 것과 두 번째는 바뀔 수 있는 객관적 기능에 관한 것이다.[2]
- 정리 1: 모든 알고리즘 쌍에 대해 a와12 a
where denotes the ordered set of size of the cost values associated to input values , is the function being optimized and , 은 함수 에서 m 회 알고리즘으로부터 주어진 일련의 비용 값을 얻을 조건부 확률이다
본질적으로 이것은 모든 함수 f가 동등할 가능성이 있을 때, 검색 과정에서 m 값의 임의적인 순서를 관찰할 확률은 검색 알고리즘에 따라 달라지지 않는다고 말한다. 정리 1은 시간 변동의 객관적 함수에 대해 "더 미묘한" NFL 결과를 설정한다.
결과 해석
NFL 결과에 대한 전통적인, 그러나 완전히 정확하지는 않은 해석은 "일반적인 목적의 범용 최적화 전략은 이론적으로 불가능하며, 한 전략이 고려 중인 특정 문제에 특화되어야만 다른 전략을 능가할 수 있다"[17]는 것이다. 몇 가지 코멘트가 순서대로 나열되어 있다.
- 범용 거의 보편적 최적기는 이론적으로 존재한다. 각 검색 알고리즘은 거의 모든 객관적 기능에서 좋은 성능을 발휘한다.[11] 따라서 컴퓨터 시간이 저렴하기 때문에 검색 알고리즘 간의 "상대적으로 작은" 차이점에 관심이 없다면, 무료 점심식사가 없다고 걱정하지 말아야 한다.
- 알고리즘은 어느 것도 문제에 특화된 것이 아닌 경우 문제에서 다른 알고리즘을 능가할 수 있다. 실제로 두 알고리즘이 모두 이 문제의 최악에 속할 수도 있다. 보다 일반적으로 Wolpert와 Macready는 알고리즘과 문제에 대한 분포 사이의 "정렬" 정도를 측정했다.[2] 한 알고리즘이 다른 알고리즘보다 분포를 더 잘 일치시킨다고 말하는 것은 둘 중 하나가 의식적으로 분포를 전문화했다고 말하는 것이 아니다; 알고리즘은 단지 운에 의해서만 잘 정렬될 수 있다.
- 실제로 일부 알고리즘은 후보 솔루션을 재평가한다. 한 번도 평가되지 않은 지원자들에게만 성능을 고려하는 이유는 알고리즘을 비교할 때 사과를 사과와 비교하는 것을 확실히 하기 위함이다. 더욱이 특정 문제에 대해 하는 다른 알고리즘에 대해 후보를 재평가하지 않는 알고리즘의 우월성은 문제에 대한 전문화와는 아무런 관련이 없을 수 있다.
- 거의 모든 객관적인 기능에서 전문화는 본질적으로 우연한 것이다. Kolmogorov 랜덤성을 정의하는 데 사용되는 범용 튜링 가공에 관한 한, 압축 불가능한, 또는 Kolmogorov 랜덤, 객관적 함수는 알고리즘에 대한 정규성이 없다. 그러므로 범용 튜링 기계에는 분명히 우월한 선택이 하나 있다고 가정해 보자. 그런 다음 해당 튜링 기계에 대해 압축할 수 없는 객관적 기능을 부여하면, 그 튜링 기계를 사용하여 측정한 바와 같이 둘 다 압축할 수 있는 경우 두 알고리즘 사이에서 선택할 수 있는 근거가 없다. 만약 선택된 알고리즘이 대부분의 알고리즘보다 더 잘 수행된다면, 그 결과는 우연이다.[11] Kolmogorov 랜덤함수는 검색 공간의 각 점에 해당하는 (랜덤) 값을 포함하는 룩업 테이블보다 작은 표현을 가지고 있지 않다. 보다 압축적으로 표현할 수 있는 함수는 정의상 Kolmogorov 랜덤이 아니다.
실제로 컴퓨터의 저장장치에 (임의와는 거리가 먼) 고압축성 객관적 기능만 들어맞고, 각 알고리즘이 거의 모든 압축함수에 대해 좋은 성능을 발휘하는 경우는 아니다. 알고리즘에 문제에 대한 사전 지식을 통합하는 데는 일반적으로 성능상의 이점이 있다. NFL 결과가 엄격한 의미에서 최적화 전문가에 대한 완전한 고용 정리를 구성하지만, 더 큰 맥락을 염두에 두는 것이 중요하다. 우선 첫째로, 인간은 함께 일하기 위한 사전 지식이 거의 없는 경우가 많다. 또 다른 예로, 사전 지식을 통합하는 것은 일부 문제에서 많은 성과를 거두지 못한다. 마지막으로 인간의 시간은 컴퓨터 시간에 비해 매우 비싸다. 회사가 인간 개조 프로그램으로 빠르게 기능 최적화를 선택하는 경우가 많다.
NFL 결과는 특수하지 않은 알고리즘의 문제점에 대해 "포터 샷"을 하는 것이 헛된 것이라는 것을 나타내지 않는다. 알고리즘이 빠른 속도로 좋은 결과를 산출하는 실제 문제의 분율을 아무도 결정하지 못했다. 그리고 이론과 전혀 상충되지 않는 실용적인 무료 점심식사가 있다. 컴퓨터에 알고리즘의 구현을 실행하는 것은 인간의 시간과 좋은 해결책의 이익에 비해 비용이 거의 들지 않는다. 알고리즘이 수용 가능한 시간 내에 만족스러운 해결책을 찾는 데 성공한다면, 적은 투자로 큰 성과를 거두었다. 알고리즘이 실패하면 거의 손실되지 않는다.
공진화
월퍼트와 맥프레디는 공진화 최적화에 무료급식이 있다는 것을 증명했다.[9] 그들의 분석은 '셀프 플레이' 문제와 비교된다. 이런 문제들 속에서 선수 세트가 힘을 합쳐 챔피언을 배출하고, 이후 멀티플레이어 게임에 1명 이상의 적대자를 참여시킨다."[9] 즉, 목표는 좋은 선수를 확보하는 것이지만 객관적인 기능은 갖추지 않는 것이다. 선수 개개인의 선량함(후보 해결책)은 타인에게 얼마나 잘 맞는지 관찰하여 평가한다. 알고리즘은 더 나은 선수들을 얻기 위해 선수들과 그들의 경기 질을 이용하려고 시도한다. 알고리즘이 가장 좋다고 생각하는 선수가 챔피언이다. Wolpert와 Macready는 어떤 공진화 알고리즘이 일반적으로 챔피언의 질에서 다른 알고리즘보다 우수하다는 것을 증명했다. 자기 플레이를 통해 챔피언을 탄생시키는 것은 진화 계산과 게임 이론에 관심이 있다. 그 결과는 챔피언을 낳지 않는 생물종의 공진화에는 적용되지 않는다.[9]
참고 항목
메모들
- ^ a b Wolpert, D. H.; Macready, W. G. (1995). "No Free Lunch Theorems for Search" (PDF). Technical Report SFI-TR-95-02-010. Santa Fe Institute. S2CID 12890367.
- ^ a b c d e f g Wolpert, D. H.; Macready, W. G. (1997). "No Free Lunch Theorems for Optimization" (PDF). IEEE Transactions on Evolutionary Computation. 1: 67–82. doi:10.1109/4235.585893.
- ^ Wolpert, David (1996). "The Lack of A Priori Distinctions between Learning Algorithms" (PDF). Neural Computation. Vol. 8. pp. 1341–1390. doi:10.1162/neco.1996.8.7.1341. S2CID 207609360.
- ^ a b c Schaffer, Cullen (1994). "A conservation law for generalization performance" (PDF). In Willian, H.; Cohen, W. (eds.). International Conference on Machine Learning. San Francisco: Morgan Kaufmann. pp. 259–265.
- ^ a b M. (2003) Streeter, M. (2003) "무료급식 결과가 유지되지 않는 두 가지 광범위한 기능 등급," 유전 및 진화 연산 – GECCO 2003, 페이지 1418–1430.
- ^ a b c d e f g Igel, C, Toussaint, M. (2004) "대상 함수의 불균일한 분포를 위한 무자유 런치 정리", 수학적 모델링 및 알고리즘 저널 3, 페이지 313–322.
- ^ a b c d e f g h i English, T. (2004) No More Hunch: 순차 검색 분석, 2004년 IEEE Congress on Evolutional Computing, 페이지 227–234.
- ^ a b c S. 드로스테, T. 얀센, 그리고 나. 베게너. 2002. "임의의 검색 경험에 의한 최적화: (A)NFL 정리, 현실적인 시나리오 및 어려운 기능," 이론 컴퓨터 과학, 제 287권, 제 1호, 페이지 131–144.
- ^ a b c d W.G. W.G. Worpert, D.H 및 Macready(2005) "진화 무료 점심", IEEE의 진화적 계산 거래, 9(6): 721–735
- ^ 또한 검색 알고리즘은 평가된 후보 솔루션의 순서를 출력하지만, 그 출력은 이 문서에서 사용되지 않는다.
- ^ a b c d e English, T. M. (2000). "Optimization Is Easy and Learning Is Hard in the Typical Function". Proceedings of the 2000 Congress on Evolutionary Computation: CEC00. 2: 924–931. doi:10.1109/CEC.2000.870741. ISBN 0-7803-6375-2. S2CID 11295575.
- ^ Lloyd, S. (2002). "Computational capacity of the universe". Physical Review Letters. 88 (23): 237901–237904. arXiv:quant-ph/0110141. Bibcode:2002PhRvL..88w7901L. doi:10.1103/PhysRevLett.88.237901. PMID 12059399. S2CID 6341263.
- ^ Li, M.; Vitányi, P. (1997). An Introduction to Kolmogorov Complexity and Its Applications (2nd ed.). New York: Springer. ISBN 0-387-94868-6.
- ^ Woodward, John R. (2009). "Computable and incomputable functions and search algorithms". IEEE International Conference on Intelligent Computing and Intelligent Systems, 2009. Vol. 1. IEEE. pp. 871–875. CiteSeerX 10.1.1.158.7782.
- ^ "only if" 부분은 다음에 의해 처음 출판되었다.
- ^ Rowe; Vose; Wright (2009). "Reinterpreting No Free Lunch". Evolutionary Computation. 17 (1): 117–129. doi:10.1162/evco.2009.17.1.117. PMID 19207090. S2CID 6251842.
- ^ Ho, Y. C.; Pepyne, D. L. (2002). "Simple Explanation of the No-Free-Lunch Theorem and Its Implications". Journal of Optimization Theory and Applications. 115 (3): 549–570. doi:10.1023/A:1021251113462. S2CID 123041865.
외부 링크
- http://www.no-free-lunch.org
- Radcliffe와 Surry, 1995년, "검색 알고리즘의 근본적 한계: 원근적인 관점에서의 진화적 컴퓨팅"(NFL에 관한 초창기 간행물, 섀퍼의 ICML 논문 직후 등장)은 월퍼트의 프리프린트를 바탕으로 하고, 다양한 형태로 이용 가능하다.
- 토마스 잉글리쉬의 NFL 출판물
- 크리스티안 이겔과 마크 뚜생에 의한 NFL 출판물
- NFL과 Darrell Whitley의 "무료 점심" 출판물
- 최적화 및 검색에 관한 David Wolpert, William Macready 및 Mario Koeppen의 오래된 출판물 목록
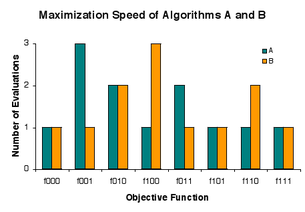
 모든
모든