Microsoft Excel의 숫자 정밀도

다른 스프레드시트와 마찬가지로 마이크로소프트 엑셀은 숫자를 기술할 수 있는 수치(정밀성이 제한됨)를 일정 개수에 불과하기 때문에 제한된 정확도로만 작업한다. 잘못된 값, infinity 및 denormalized 숫자와 관련된 일부 예외를 제외하고 Excel은 IEEE 754 규격에서^[1] 이중 정밀 부동 소수점 형식으로 계산한다(숫자 이외에 Excel은 몇 가지 다른 데이터 유형을^[2] 사용한다). 비록 엑셀 30소수 자릿수를 표시할 수 있지만,을 위해 정밀 15상당한 수치에 및 계산은 오히려 5개 현안:라운드 off,[3]절단, 2진 법 저장, 피연산자의 계산 속의 편차가 누적 및 최악의:차감하 레에서 취소될 예정이다 정확도를 가지고 있다고 누워 있다.sp. 크기가 비슷한 값의 뺄셈에서 'catastriculative discovery'

정확도 및 이진 저장

상단 그림에는 Excel의 분수 1/9000이 표시된다. 이 숫자는 무한대의 문자열인 십진법 표현이지만, 엑셀은 선행 15자리 숫자만 표시한다. 두 번째 줄에서는 1번이 분수에 추가되고, 다시 엑셀은 15개의 숫자만 표시한다. 세 번째 줄에서는 엑셀을 사용하여 합에서 하나를 뺀다. 십진수 이후 합이 11초밖에 되지 않기 때문에 '1'을 빼면 진정한 차이는 3 0초, 그 다음에 11 1의 줄을 잇는다. 그러나 엑셀이 보고한 차이는 3 0, 15자리 문자열은 13 1초, 2자리의 오차가 있다. 따라서 엑셀이 계산한 숫자는 표시된 숫자가 아니다. 더구나 엑셀의 대답에 나오는 오류는 단순히 반올림 오차가 아니라 '취소'라고 하는 부동소수 계산에 영향을 주는 것이다.

엑셀 계산의 부정확성은 중요한 수치 15개의 정밀도로 인해 오류보다 더 복잡하다. 엑셀이 이진 형식으로 숫자를 저장한 것도 정확도에 영향을 미친다.^[4] 예를 들어, 아래 그림은 x의 여러 값에 대한 단순 덧셈 1 + x - 1을 표로 표시한다. x의 모든 값은 15번째 소수점부터 시작되므로 엑셀은 이를 고려해야 한다. 합계 1 + x를 계산하기 전에 엑셀은 이진수로 먼저 x에 근사치를 한다. 이 x의 이진 버전이 2의 단순한 힘이라면, x에 대한 15자리 소수 근사치가 합에 저장되며, 그림의 상위 두 예는 오류 없이 x의 회복을 나타낸다. 세 번째 예제에서 x는 더 복잡한 이진수, x = 1.110111⋯111×2⁻⁴⁹ (모두 15비트)이다. Here the 'IEEE 754 double value' resulting of the 15 bit figure is 3.330560653658221E-15, which is rounded by Excel for the 'user interface' to 15 digits 3.33056065365822E-15, and then displayed with 30 decimals digits gets one 'fake zero' added, thus the 'binary' and 'decimal' values in the sample are identical only in display, the values associa셀이 있는 ted는 서로 다르다(1.110111111111000000000000000000000000000000000000000000000000000000×2⁻⁴⁹ 대 1.110111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111⁻⁴⁹ 다른 스프레드시트에서도 마찬가지로, '더블'의 53비트 맨티사(예: 1에서 8 사이의 16자리, 0.5에서 1에서 8에서 10 사이의 15자리만)에 정확히 저장할 수 있는 다른 소수 자릿수의 처리가 다소 어려워 '최적'을 해결한다. 네 번째 예제에서 x는 단순한 이진수와 같지 않은 십진수 숫자다(세 번째 예제의 이진수와 표시된 정밀도에 동의함). 십진 입력은 이진수로 근사치한 다음 십진수를 사용한다. 그림의 이 두 가지 중간 예는 일부 오류가 발생했음을 보여준다.

마지막 두 예는 x가 다소 작은 숫자일 경우 어떤 일이 발생하는지 예시한다. 마지막 예에서 두 번째 예에서 x = 1.110111⋯111 × 2⁻⁵⁰; 모두 합쳐서 15비트. 이항은 2의 단일 검정력(이 예에서는 2⁻⁴⁹)으로 매우 조잡하게 대체되며, 십진수 등가물이 사용된다. 아래 예에서, 위 2진수와 표시된 정밀도와 동일한 십진수는 그럼에도 불구하고 2진수와 다른 근사치로 추정되며, 15개의 유의한 숫자로 잘라내어 1 + x - 1에 기여하지 않고 x = 0으로 이어진다.^[5]

단순한 2의 힘이 아닌 x의 경우, x가 상당히 큰 경우에도 1 + x - 1의 눈에 띄는 오차가 발생할 수 있다. 예를 들어 x = 1/1000인 경우 1 + x - 1 = 9.9999999999989 × 10인⁻⁴ 13번째 유의 수치의 오류. 이 경우 엑셀이 단순히 십진수를 더하고 빼서 이진수로의 변환을 피하고 다시 십진수로의 변환을 피한다면 반올림 오차는 발생하지 않을 것이고 실제로 정확도가 더 좋을 것이다. 엑셀에는 "표시된 대로 정밀도를 설정"^[6]하는 옵션이 있다. 이 옵션을 사용하면 상황에 따라 정확도가 더 좋아지거나 나빠질 수 있지만, 엑셀이 무엇을 하고 있는지 정확히 알 수 있다.(선택한 정밀도만 유지되며, 이 옵션을 반대로 하여 여분의 자릿수를 복구할 수 없다.) 이 링크에서 몇 가지 유사한 예를 찾아볼 수 있다.^[7]

요컨대, 15번째 유의미한 수치를 넘어 숫자를 자르는 것과 함께 제한된 이진수로 숫자를 나타내는 조합에 의해 다양한 정확도 행동이 도입된다.^[8] Excel의 유의미한 수치 15개를 초과하는 숫자에 대한 처리는 단지 15개의 유의한 수치만으로 직접 작업하는 것보다 더 나은 정확도를 계산의 최종 몇 개의 유의한 수치들에 기여하기도 하며, 때로는 그렇지 않은 경우도 있다.

바이너리 표현으로 변환하고 십진법으로 다시 변환하는 이면에 대한 추론과 엑셀과 VBA의 정확성에 대한 자세한 내용은 이 링크를 참조하십시오.^[9]

1. '= 1 + x - 1' 과제의 단점은 'fp-math 약점'과 '엑셀이 어떻게 처리하느냐'의 조합인데, 특히 엑셀의 라운딩이 그렇다. Excel은 대부분의 결과에 대해 평균적으로 IEEE 이중표현의 마지막 3비트를 자르는 반올림 및/또는 '0으로 스냅'을 한다. 이 동작은 괄호 안의 공식을 '=(1 + 2^-52 - 1)'로 설정하여 전환할 수 있다. 그 작은 가치도 살아남는다는 것을 알게 될 것이다. 이 경우 1.0000000000000000000000000000000000000000000000000000001은 첫 번째, 마지막은 '2^-52'의 경우 작은 값이 사라진다.

2. 그것은 생존하는 두 개의 클린 파워일 뿐만 아니라, 소수 1이 추가되면 53비트 내에 포함되는 비트들로 구성된 값의 조합이다. 대부분의 십진수 값은 2진수에서 깨끗한 유한표현이 없기 때문에 위와 같은 과제에서 '반올림'과 '취소'를 겪게 된다.

예: 소수점 0.1은 IEEE 이중 표현 0(1.100110011001100110011001100110011001100110011001100110011001010 곱하기 2^-4)을 가지며 140737488355328.0(이것은 2^47)에 추가되면 처음 두 개를 제외한 모든 비트가 손실된다. 따라서 '= (140737488355328.0 + 0.1 - 140737488358.0)에서 www.weitz.de/ieee(64비트)과 함께 계산된 0.09375로 계산되고 공식 주위에 괄호가 있는 엑셀에서 돌아온다. 이 효과는 대부분 의미 있는 라운딩으로 관리할 수 있는데 엑셀은 이를 적용하지 않고 사용자에게 달려 있다.

말할 필요도 없이, 다른 스프레드시트에도 유사한 문제가 있는 반면, LibreOffice Calc는 보다 공격적인 라운딩을 사용하는 반면, gumeric은 정밀도를 유지하고 사용자에게 '부족'이 보이도록 하기 위해 노력한다.

정밀도가 정확도를 나타내지 않는 예

이 구간은 확장이 필요하다. 추가하면 도움이 된다.(2010년 4월)

통계함수

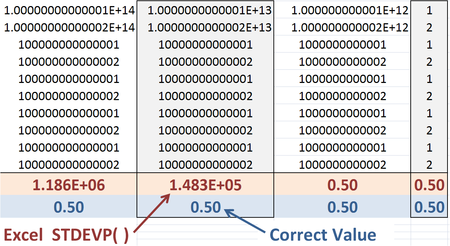
엑셀 제공 기능의 정확도가 문제가 될 수 있다. Micah Altman 등에서는 다음과 같은 예를 제시한다.^[10] 다음이 제공한 모집단 표준 편차:

${\displaystyle{\sqrt{\bar{x}}^{2}}:{n}}}}={\sqrt{n}}}}{\sigma \왼쪽[\Sigma x\오른쪽]^{n}\},}$

수학적으로 다음과 같다:

${\displaystyle {\sqrt {\frac {n\Sigma x^{2}-\왼쪽(\Sigma x\오른쪽)^{2}}:{n^{2}}\ .}$

그러나 첫 번째 형태는 x의 큰 값에 대해 더 나은 수치 정확도를 유지하는데, 그 이유는 x와 x의_av 차이가 훨씬 큰 숫자 numbersx와 (σx)의 차이보다 덜 반올림되기 때문이다.² 그러나 내장된 Excel 함수 STDEVP()는 계산적으로 더 빠르기 때문에 덜 정확한 제형을 사용한다.^[11]

"호환성" 함수 STDEVP와 "정합성" 함수 STDEV 모두.Excel 2010의 P는 주어진 값 집합에 대한 0.5 모집단 표준 편차를 반환한다. 그러나 수치적 부정확성은 Excel 2010이 발견한 잘못된 표준 편차가 0이 되는 10을¹⁵ 포함하도록 기존 수치를 확장함으로써 이 예를 사용하여 여전히 보일 수 있다.

감산 결과의 감산

두 개의 셀이 두 개의 개별 값을 저장하면서 동일한 숫자 값을 표시할 수 있기 때문에 간단한 감산을 수행하면 오류가 발생할 수 있다. 다음의 셀이 다음과 같은 숫자 값으로 설정된 시트에서 이러한 예가 발생한다.

${\displaystyle A1:=28.552}$

${\displaystyle A2:=27.399}$

${\displaystyle A3:=26.246}$

다음 셀은 다음 공식을 포함한다.

${\디스플레이 스타일 B1:=A1-A2}$

${\디스플레이 스타일 B2:=A2-A3}$

Both cells ${\displaystyle B1}$ and ${\displaystyle B2}$ display ${\displaystyle 1.1530}$. However, if cell ${\displaystyle C1}$ contains the formula ${\displaystyle B1-B2}$ then ${\displaystyle C1}$ does not display ${\displaystyle 0}$ as would be expected, but displays $$${\displaystyle -3.55271}$ ${\displaystyle E}$- ${\displaystyle 15}$ ${\displaystyle -3.55271E-15}$ 대신$$

The above is not limited to subtractions, try '=1+1,405*2^-48' in one cell, Excel rounds the display to 1,00000000000000000000, and '=0,9+225179982494413*2^-51' in another, same display (in the range above 1 / below 1 the rounding is different, which hits most decimal or binary magnitude changes) above, different rounding for value and display, vio골드버그의 기본 요건 중 하나인 '모든 컴퓨터 과학자가 부동 소수점 산수에 대해 알아야 할 것'(fp-math의 '성서'에 가깝거나 그 이하)에는 '사용자에게 투명하도록 하는 것이 중요하다'고 명시되어 있다. 예를 들어 계산기에서 표시값의 내부표현이 표시장치와 같은 정밀도로 반올림되지 않으면 추가 조작의 결과는 숨겨진 숫자에 따라 달라지며 사용자에게 예측할 수 없는 것으로 나타난다(문제는 Excel에만 국한되지 않는다, 예를 들어 LibreOffice calcal은 유사하게 작용한다).

반올림 오차

사용자 계산은 반올림 오류가 문제가 되지 않도록 세심하게 구성되어야 한다. 2차 방정식을 풀 때 다음과 같은 예가 발생한다.

${\displaystyle ax^{2}+bx+c=0\ .}$

이 방정식의 해법(근)은 정확히 이차 공식에 의해 결정된다.

${\displaystyle x={\frac {-b\pm {\sqrt{b^{2}-4ac}}{2a}}.}$

이들 뿌리 중 하나가 다른 뿌리에 비해 매우 클 때, 즉 제곱근이 값 b에 가까울 때, 반올림(취소?)으로 인해 두 용어의 뺄셈에 해당하는 뿌리의 평가가 매우 부정확해진다.

제곱근에 대한 테일러 시리즈 공식을 사용하여 반올림 오차를 결정할 수 있다.

${\displaystyle {\sqrt{b^{2}-4ac}=b\{1-{\frac}{b^{2}}}}}\sqrt {1-{\frac}{2ac}{b^{2}}+{2a^{}}}}{b^{4}}+cdots.}$

결과적으로,

${\displaystyle b-{\sqrt{b^{2}-4ac}\b\left\frac {2ac}{b^{2}}-{2a^{2}c^{2}}:{b^{4}}}}+\cdots \right)}}$

b가 커질수록 첫 번째 생존 용어는 다음과 같이 말하는 것을 나타낸다.

${\displaystyle \varepsilon ={\frac {2ac}{b}},}$

점점 작아진다. b와 제곱근의 숫자는 거의 같게 되고, 차이는 작아진다.

${\displaystyle b-{\sqrt {b^{2}-4ac}\c}\cHB+\varepsilon .}$

이런 상황에서 모든 중요한 수치는 b를 표현하는 데 들어간다. 예를 들어 정밀도가 15자리 숫자인데, 이 두 자리 숫자 b와 제곱근은 15자리 숫자와 같다면, 차이는 difference 대신 0이 된다.

더 나은 정확도는 아래에 설명된 다른 접근법을 통해 얻을 수 있다.^[13] 만약 우리가 두 뿌리를 r과 r로 나타낸다면, 2차 방정식은 다음과 같이 쓰여질 수 있다.

${\displaystyle \left(x-r_{1}\right)\left(x-r_{2}\right)=x^{2}-\left(r_{1}+r_{2}\right)x+r_{1}\{2}=0.}$

루트 r >> r , , , 두 가지 형태의 합계(r + r ) ≈ r과 비교는 대략 다음과 같이 나타난다.

${\displaystyle r_{1}\대략 -{\frac {b}{a},}$

하는 동안에

${\displaystyle r_{1}\ r_{2}={\frac {c}{a}}}.}$

따라서 대략적인 형태는 다음과 같다.

${\displaystyle r_{2}={\frac {c}{a\r_{1}}\대략 -{\frac {c}{b}}.}$

이러한 결과는 반올림 오차의 대상이 되지 않지만, b가² ac에 비해 크지 않으면 정확하지 않다.

요컨대 엑셀을 이용하여 이 계산을 할 때 뿌리가 값에서 멀어짐에 따라 계산 방법이 2차 공식에 대한 직접 평가에서 다른 방법으로 전환되어 반올림 오차를 제한해야 한다는 것이다. 전환점 방법은 계수 a와 b의 크기에 따라 달라진다.

그림에서 엑셀은 c = 4와 c = 4 × 10의⁵ 경우 2차 방정식 x² + bx + c = 0의 최소 루트를 찾는 데 사용된다. 2차 공식을 사용한 직접 평가와 넓은 간격의 뿌리에 대해 위에서 설명한 근사치와의 차이는 b.와 비교하여 표시된다. 처음에는 넓은 간격의 루트 방법이 더 큰 b-값에서 더 정확해지기 때문에 방법들 간의 차이가 감소한다. 그러나 일부 b-값을 벗어나면 반올림으로 인해 2차 공식(작은 b-값에 좋음)이 악화되는 반면, 넓은 간격의 루트 방법(큰 b-값에 좋음)은 계속 개선되기 때문에 차이가 커진다. 전환점 방법은 큰 점으로 표시되며, 더 큰 c-값의 경우 더 크다. 큰 b 값에서 위쪽으로 기울어진 곡선은 2차 공식에서 엑셀의 반올림 오류로, 이 경우 불규칙한 동작으로 곡선이 구불구불하게 된다.

정확성이 문제가 되는 다른 분야는 통합의 수치 계산 영역과 미분방정식의 해법이다. 심슨의 규칙, 룬게-쿠타 방법, 슈뢰딩거 방정식에 대한 누메로프 알고리즘 등이 그 예다.^[14] 어플리케이션용 Visual Basic을 이용하면 엑셀에서 이러한 방법 중 하나를 구현할 수 있다. 수치적 방법은 기능이 평가되는 그리드를 사용한다. 기능은 그리드 포인트 사이에 보간되거나 인접 그리드 포인트를 찾기 위해 외삽될 수 있다. 이러한 공식은 인접한 값의 비교를 포함한다. 그리드의 간격을 매우 미세하게 맞추면 반올림 오차가 발생하며, 사용하는 정밀도가 낮을수록 반올림 오차가 심해진다. 넓게 간격을 두면 정확성이 떨어진다. 수치적 절차를 피드백 시스템으로 생각한다면, 이 계산 노이즈는 시스템에 적용되는 신호로 볼 수 있으며, 이는 시스템을 주의 깊게 설계하지 않는 한 불안정성으로 이어질 것이다.^[15]

VBA 내 정확성

엑셀은 기본적으로 8바이트 숫자로 작동하지만 VBA는 다양한 데이터 유형을 가지고 있다. 이중 데이터 유형은 8바이트, 정수 데이터 유형은 2바이트, 범용 16바이트 변종 데이터 유형은 VBA 변환 함수 CDec를 사용하여 12바이트 소수 데이터 유형으로 변환할 수 있다.^[16] VBA 계산에서 가변 유형을 선택하려면 스토리지 요구 사항, 정확성 및 속도를 고려해야 한다.

참조