음극 피드백 앰프

음극 피드백 앰프(또는 피드백 앰프)는 음극 피드백이 원래 신호에 반대하도록 입력에서 출력의 일부를 빼는 전자 증폭기다.^[1]적용된 부정적인 피드백은 성능을 향상시킬 수 있고(게인 안정성, 선형성, 주파수 응답, 스텝 응답) 제조나 환경에 따른 파라미터 변동에 대한 민감도를 줄일 수 있다.이러한 장점 때문에 많은 증폭기와 제어 시스템은 부정적인 피드백을 사용한다.^[2]

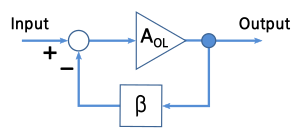
다이어그램에 표시된 것처럼 이상적인 음극 피드백 앰프는 세 가지 요소로 구성된 시스템이다(그림 1 참조).

• 이득 A가_OL 있는 앰프,
• 출력 신호를 감지하고 어떤 식으로든 변환할 수 있는 피드백 네트워크 β(예: 감쇠 또는 필터링
• 입력과 변환된 출력을 결합한 감산기(그림의 원) 역할을 하는 합계 회로

개요

기본적으로 전력 이득을 제공하는 모든 전자 장치(예: 진공관, 양극성 트랜지스터, MOS 트랜지스터)는 비선형이다.부정적인 피드백 트레이드는 더 높은 선형성(왜곡 감소)을 위해 이득을 얻으며 다른 이익을 제공할 수 있다.올바르게 설계되지 않은 경우, 음의 피드백을 가진 증폭기는 피드백이 양성으로 인해 일부 상황에서 불안정해져 진동과 같은 원치 않는 행동을 유발할 수 있다.벨 연구소의 해리 나이키스트가 개발한 나이키스트 안정성 기준은 피드백 증폭기의 안정성을 연구하는데 사용된다.

피드백 증폭기는 다음과 같은 특성을 공유한다.^[3]

찬성:

• 피드백 유형에 따라 입력 임피던스를 증가시키거나 감소시킬 수 있다.
• 피드백 유형에 따라 출력 임피던스를 증가시키거나 감소시킬 수 있다.
• 충분히 도포할 경우 전체 왜곡 감소(선형성 증가)
• 대역폭을 증가시킨다.
• 구성요소 변동에 대한 이득을 약화시킨다.
• 앰프의 스텝 응답을 제어할 수 있다.

반대:

• 주의 깊게 설계하지 않으면 불안정해질 수 있다.
• 증폭기 게인이 감소한다.
• 음극 피드백 앰프(폐쇄 루프 앰프)의 입력 및 출력 임피던스는 피드백(개방 루프 앰프)이 없는 앰프의 이득에 민감하게 되며, 이는 예를 들어, 개방 루프 게인의 매개변수 변화 또는 비선형성으로 인해 개방 루프 게인의 변동에 이러한 임피던스를 노출시킨다.
• 불충분하게 도포될 경우 왜곡의 구성(청각성 증가)을 변경한다.

역사

Paul Voigt는 1924년 1월에 음의 피드백 증폭기를 특허를 냈지만, 그의 이론은 상세하지 않았다.^[4]해롤드 스티븐 블랙은 1927년^[5] 8월 2일(미국 특허 210만2,671, 1937년^[6] 발행) 벨 연구소(뉴저지 대신 맨해튼에 위치)에 근무하던 중 라코완나 페리(호보켄 터미널에서 맨해튼까지)의 승객으로 있을 때 음극 피드백 앰프를 독자적으로 발명했다.블랙은 전화 송신에 사용되는 리피터 증폭기의 왜곡을 줄이는 작업을 하고 있었다.뉴욕타임즈 카피의 빈칸에 그는 그림 1에서 발견된 도표와 아래에 도출된 방정식을 기록했다.^[7][8]1928년 8월 8일, 블랙은 그의 발명품을 미국 특허청에 제출했는데, 이 특허권을 발행하는 데 9년 이상이 걸렸다.블랙은 나중에 "이 개념이 확립된 신념에 반하여 처음에는 특허청이 그것이 효과가 있을 것이라고 믿지 않았기 때문"이라고 썼다.^[9]

클래식 피드백

두 개의 일방적인 블록의 모델을 사용하여 피드백의 몇 가지 결과를 간단하게 도출한다.

이득감소

아래에서 피드백이 있는 앰프의 전압 이득인 폐쇄 루프 게인 A는_FB 피드백이 없는 앰프의 게인 A와 입력에 적용되는_OL 출력 신호의 양을 좌우하는 피드백 계수 β의 측면에서 도출된다(그림 1 참조).일반적으로 개방형 루프 게인 A는_OL 주파수와 전압 모두의 함수일 수 있다. 피드백 파라미터 β는 앰프 주위로 연결된 피드백 네트워크에 의해 결정된다.작동 증폭기의 경우, 피드백 네트워크가 β를 0과 1 사이에 설정하기 위해 전압 분배기를 형성하는 두 개의 저항을 사용할 수 있다.이 네트워크는 (a) 등화/음향 제어 회로 또는 (b) 구성 오실레이터에서와 같이 주파수 의존형 폐쇄 루프 게인(closed-loop gain)을 제공하는 콘덴서 또는 인덕터와 같은 반응 요소를 사용하여 수정할 수 있다.피드백이 있는 앰프의 이득은 전압 피드백이 있는 전압 앰프의 경우 아래에 도출된다.

피드백이 없으면 입력 전압 V′_in이 앰프 입력에 직접 가해진다.출력 전압은

${\displaystyle V_{\text{out}}=A_{\text{OL}\cdot V'_{\text{in}}.}$

이제 감쇠 피드백 루프가 감쇠기 입력에 적용되는 회로 입력 전압 V에서_in 다른 감쇠기 입력에 뺄 수 있도록 출력의 부분$$$\beta {\displaystyle }$ β β ${\displaystyle {}_{}{\text{out}}_{}}${\$displaystyle \beta \cdot V_{\text{out}}}}$을 감쇠기 입력 중 하나에 적용한다고 가정합시다.앰프 입력에 적용된 감산 결과는

${\displaystyle V'_{\text{in}=V_{\text{in}-\beta \cdot V_{\text{out}}.}$

첫 번째 표현에서 V _infor을 대신하여

${\displaystyle V_{\text{out}}=A_{\text{OL}}(V_{\text{in}-\beta \cdot V_{\text{out}).}$

재배열:

${\displaystyle V_{\text{out}(1+\beta \cdot A_{\text}){\text{OL}}}=V_{\text{in}}\cdot A_{\text}OL}}.}$

그런 다음 피드백이 있는 앰프의 이득, 즉 폐쇄 루프 이득이라고 하는 A는_FB 다음과 같이 주어진다.

${\displaystyle A_{\text{FB}}={\frac {V_{\text{out}}}{V_{\text{in}}}}={\frac {A_{\text}}}}}}{\text}}}}}}}}}{\frac {A_{\text}}}}}OL}}{1+\베타 \cdot A_{\text{OL}}}.}$

A_OL ≫ 1, A ≈ 1 / β_FB 및 유효 증폭(또는 폐쇄 루프 이득) A는_FB 피드백 상수 β에 의해 설정되며, 따라서 피드백 네트워크, 일반적으로 단순 재현 가능한 네트워크로 설정되므로 증폭 특성을 단순화 및 안정화한다.β A_OL = -1의 조건이 있는 경우, 앰프는 무한 증폭을 가지고 있다 – 그것은 오실레이터가 되었고, 시스템이 불안정하다.게인 피드백 제품 β A의_OL 안정성 특성은 나이키스트 플롯(주파수의 파라메트릭 함수로 게인/위상 시프트의 극성도)에 표시하여 조사하는 경우가 많다.더 단순하지만 덜 일반적인 기법은 보드 그림을 사용한다.

L = -β A_OL 조합은 피드백 분석에서 공통적으로 나타나며 루프 게인이라고 불린다.조합(1 + β A_OL)도 공통적으로 나타나며, 다양한 명칭을 감응 계수, 반환 차이 또는 개선 계수로 한다.^[10]

용어 요약

• 개방형 루프 게인 = ${\displaystyle {\text{OL}}_{}}$ ${\$$OL}}$
• 폐쇄 루프 게인 = $A{\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{{}_{}}{\mathrm{}}}$ 1${\displaystyle \frac{}{}}$+ ${\displaystyle \frac{\beta }{}}$ ${\displaystyle \frac{\cdot }{}}$ ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{{\text{OL}}_{}}{}}$ ${\$$OL}}{1+\베타 \cdot A_{\text{$$OL}}}$
• 피드백 계수 = $\beta {\displaystyle }$ ${\displaystyle \beta }$
• 노이즈 게인 = $1{\displaystyle \mathrm{}}$/ ${\displaystyle \beta }$ ${\displaystyle$ 1$/\beta }$
• 루프 게인 = -${\displaystyle \beta }$ ${\displaystyle \cdot }$ ${\displaystyle {}_{}}$ ${\displaystyle {\text{OL}}_{}}$ ${\$ -$\beta \cdot A_{\text{$$OL}}$
• 민감도 계수 = $1{\displaystyle \mathrm{}}$+ ${\displaystyle \beta }$ β${\displaystyle {}_{}}$ ${\displaystyle {\text{OL}}_{}}$ ${\$ 1$+\beta \cdot A_{\text{$$OL}}$

대역폭 확장

피드백은 증폭기 게인을 낮추는 비용으로 증폭기의 대역폭을 확장하는데 사용될 수 있다.^[15]그림 2는 그러한 비교를 보여준다.그 수치는 다음과 같이 이해된다.피드백이 없으면 이 예에서 소위 오픈 루프 이득은 다음과 같은 단시간 정합 주파수 응답을 가진다.

${\displaystyle A_{\text{OL}}(f)={\frac {A_{0}}{1+jf/f_{\text{C}},}$

여기서 f는_C 앰프의 컷오프 또는 코너 주파수: 이 예에서_C f = 10Hz⁴, 0 주파수 A = 10V₀⁵/V에서의 게인.이 그림은 이득이 코너 주파수까지 평평하게 나온 다음 떨어지는 것을 보여준다.피드백이 있을 때, 앞 절의 공식에 나타난 바와 같이, 이른바 폐쇄 루프 이득이 된다.

${\displaystyle {\reasoned}A_{\text{FB}}(f)&={\frac {A_{\text{OL}}{1+\베타 A_{\text{OL}}\\&={\frac {A_{0}/(1+jf/f_{\text{C})}{1+\beta A_{0}/(1+jf/f_{\text{C})}\\\\={0}{0}{1+jf/f_{c}}}}}}}}{{{1+jfrac{{{{{{{c}텍스트텍스트ext}}}}}}}}{{{{{{{{{{1+jf}}}}}}}}}}C}+\beta A_{0}\\&={\frac {A_{0}}{{{0}}}}{{1+\beta A_{0}}}}}}\좌측(1+j{frac{f}{1+\beta A_{0}f_{\text}{\cext}}}}C}}}\오른쪽)}}.\end{정렬}}}$

마지막 식을 보면 피드백 증폭기는 여전히 단시간 정속적인 동작을 가지고 있지만, 현재 코너 주파수는 개선 계수(1 + β A₀)에 의해 증가하며, 제로 주파수에서의 이득은 정확히 동일한 계수만큼 감소하였다.이러한 행동을 이득-대역폭 트레이드오프라고 한다.그림 2에서 (1 + β A₀) = 10이므로³ A_FB(0) = 10⁵ / 10³ = 100 V/V, f는_C 10⁴ × 10³ = 10⁷ Hz로 증가한다.

다중극

클로즈루프 이득이 위의 예시의 단일 극이 아닌 여러 극을 갖는 경우 피드백은 복잡한 극(실제 및 가상의 부분)을 초래할 수 있다.2극 케이스의 경우, 그 결과는 피드백 증폭기의 코너 주파수 근처에 있는 주파수 응답에서 정점을 찍고 그 스텝 응답에서 링잉과 오버슈트를 하고 있다.세 개 이상의 극의 경우 피드백 증폭기가 불안정해지고 진동할 수 있다.이득 마진과 단계 마진에 대한 논의를 참조하십시오.자세한 내용은 산센을 참조하십시오.^[16]

신호 흐름 분석

두 자율적으로 도입의 공식 뒤에 있는 교장 이상화는 네트워크의 분단(개별적으로 결정했다 그, 자기는 전송 함수), 자주"회로 분할"[17]이 예로 사단을 언급하는 전방 증폭 불록과 수수료로 불려에 대한 간단한 예이다.dback블록실용적인 증폭기에서 정보 흐름은 여기에 보이는 것처럼 단방향적이지 않다.^[18]종종 이러한 블록은 쌍방의 정보 전송을 포함하기 위해 이중 포트 네트워크로 간주된다.^[19][20]그러나 특히 관련된 피드백이 글로벌하지 않고 로컬(즉, 입력 및/또는 출력 단자와 일치하지 않는 노드를 포함하는 네트워크 내의 피드백)인 경우 앰프를 이 양식에 캐스팅하는 것은 비교가 안 되는 작업이다.^[21][22]

이러한 더 일반적인 경우에서, 대신 반송률 방법이나 점증상 이득 모델과 같은 신호 흐름 분석을 기반으로 한 일부 분석을 사용하여 다이어그램에 있는 블록으로 분할하지 않고 앰프를 더 직접적으로 분석한다.^[24][25][26]초마는 신호 흐름 접근법에 대해 다음과 같이 말한다.^[27]

" 피드백 네트워크 분석 문제에 대한 블록 다이어그램과 2포트 접근 방식과는 대조적으로, 신호 흐름 방법은 개방 루프와 피드백 서브회로의 일방적 또는 양자적 특성에 대한 선험적 가정을 요구하지 않는다.또한 상호 독립된 개방 루프 및 피드백 하위 회로 전송 기능에 근거하지 않으며, 피드백을 전체적으로만 구현하도록 요구하지 않는다.실제로 신호 흐름 기법은 개방 루프와 피드백 서브회로를 명시적으로 식별할 필요도 없다.따라서 신호 흐름은 기존의 피드백 네트워크 분석의 만연한 폐해를 제거하지만 또한 계산적으로 효율적이라는 것을 증명한다."

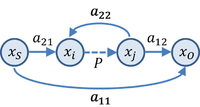
이 제안에 따라 그림에는 음극 피드백 앰프에 대한 신호 흐름 그래프가 표시되며, 이 그래프는 다미코 외 에 의해 1 뒤에 패턴으로 표시된다.^[23]이들 저자에 이어 표기법은 다음과 같다.

"변수 x_S, x는_O 입력 및 출력 신호를 나타내며, 더욱이 제어(또는 임계) 매개변수 P를 통해 함께 연결된 x, x라는_ij 두 개의 다른 일반 변수가 명시적으로 표시된다.변수 a는_ij 중량 분기다.변수 x_i, x_j 및 제어 파라미터 P, 제어 제너레이터 모델 또는 회로의 두 노드에서 전압과 전류 사이의 관계.

컨트롤 매개 변수, P설정[후]는 입력과 출력 사이의 용어 a11는 기능 0으로 했다.;그 출력과 가변 xj의 용어 a12은 전송 함수[후]은 입력 소스로 설정하면 xS, 0으로, 용어 a21 소스 변수와 내부 variable, 사이의 전달 함수를 나타냅니다. 크실 때 t제어 변수 x는_j 0으로 설정된다(즉, 제어 매개변수 P가 0으로 설정된 경우). 용어 a는₂₂ 제어 매개변수를 설정하는 독립 변수와 제어되는 내부 변수 사이의 관계, P와 입력 변수 x를_S 0으로 설정한다."

이 그래프를 사용하여, 이 저자들은 통제된 소스 관계를 정의하는_j 제어 매개변수 P의 관점에서 일반화된 게인식을 도출한다 x = Px_i:

${\displaystyle x_{\text{O}}=a_{11}x_{\text{S}}+a_{12}x_{j}}$

${\displaystyle x_{i}=a_{21}x_{\text{S}}+a_{22}x_{j}}}$

${\displaystyle x_{j}=Px_{i}}$

이러한 결과를 결합하여 이득은 다음과 같이 주어진다.

${\displaystyle {\frac {x_{\text}O}}{x_{\text{S}}}}=a_{11}+{\frac {a_{12}a_{21}P}{1-Pa_{22}}}}.}$

이 공식을 이용하려면 특정 증폭기 회로에 대한 중요한 제어 선원을 식별해야 한다.예를 들어 P는 다미코 외 연구진에서 볼 수 있듯이 2포트 네트워크에서 제어된 소스 중 하나의 제어 매개변수가 될 수 있다.^[23]다른₂₁ 예로 a₁₂ = a = 1, P = A, a₂₂ = –β(음극 피드백) 및₁₁ a = 0(피드포워드 없음)을 취하면 단방향 블록 2개로 단순 결과를 되찾는다.

2포트 피드백 분석

신호 흐름 분석 섹션에서 언급한 바와 같이, 어떤 형태의 신호 흐름 분석은 음극 피드백 앰프를 처리하는 가장 일반적인 방법이지만, 2-포트로서의 표현은 교과서에 가장 자주 제시되며 여기에 제시된다.앰프의 2블록 회로 칸막이를 유지하지만 블록이 양방향일 수 있다.이 방법의 몇 가지 단점은 마지막에 기술되어 있다.

전자 증폭기는 전류나 전압을 입력과 출력으로 사용하기 때문에 4가지 유형의 증폭기(두 가지 출력 중 어느 것이든 가능한 두 가지 입력 중 하나)가 가능하다.증폭기 분류를 참조하십시오.피드백 증폭기의 목적은 네 가지 유형의 증폭기 중 하나일 수 있으며, 그 자체가 이러한 유형의 하나일 수 있는 오픈 루프 증폭기와 반드시 같은 유형은 아니다.그래서 예를 들어, 수술 앰프(전압 증폭기)를 대신하여 전류 증폭기를 만들 수 있다.

모든 유형의 음극 피드백 증폭기는 2포트 네트워크의 조합을 사용하여 구현할 수 있다.2포트 네트워크에는 4가지 유형이 있으며, 원하는 증폭기의 유형은 2포트 선택과 다이어그램에 표시된 4가지 연결 위상 중 하나를 선택하도록 지시한다.이러한 연결은 일반적으로 직렬 또는 션트(병렬) 연결로 불린다.^[29][30]다이어그램에서 왼쪽 열에는 분로 입력이 표시되고 오른쪽 열에는 직렬 입력이 표시된다.맨 위 행에는 직렬 출력이 표시되고 맨 아래 행에는 션트 출력이 표시된다.연결과 두 포트의 다양한 조합은 아래 표에 열거되어 있다.

피드백 증폭기 유형	입력접속	출력 연결	이상적인 피드백	2포트 피드백
현재	분트	시리즈	CCCS	g자형
트랜스저항	분트	분트	CCVS	y-beats
전도성	시리즈	시리즈	VCCS	z-ray
전압	시리즈	분트	VCVS	h-11

예를 들어, 전류-피드백 앰프의 경우, 출력의 전류가 피드백을 위해 샘플링되고 입력 시 전류와 결합된다.따라서 피드백은 (출력) 전류 제어 전류 소스(CCCS)를 사용하여 이상적으로 수행되며, 2포트 네트워크를 사용한 불완전한 실현도 CCCS를 통합해야 한다. 즉, 피드백 네트워크에 대한 적절한 선택은 g-모수 2포트다.여기서는 대부분의 교과서에 사용되는 2포트 방법을 제시하며,^{[31][32][33][34]} 무증상 이득 모델에 관한 기사에서 다룬 회로를 사용한다.

그림 3은 피드백 저항기 R을_f 가진 2-트랜지스터 앰프를 보여준다.목표는 이 회로를 분석하여 게인, 부하에서 앰프를 들여다보는 출력 임피던스, 소스에서 앰프를 들여다보는 입력 임피던스 등 세 가지 항목을 찾는 것이다.

피드백 네트워크를 이중 포트로 교체

첫 번째 단계는 피드백 네트워크를 2포트(two-port)로 대체하는 것이다.투포트 안에 들어가는 구성 요소는?

2포트 입력면에는 R이_f 있다.R의_f 우측에 있는 전압이 변화하면 입력 트랜지스터의 베이스로 들어가는 전류에서 차감되는 R의_f 전류를 변화시킨다.즉, 2포트 입력면은 저항기 R의₂ 상단의 전압에 의해 제어되는 종속 전류원이다.

앰프의 두 번째 단계는 입력 트랜지스터의 수집기에서 전압을 R의₂ 상단으로 전송하는 전압 추종자일 뿐이라고 말할 수 있다.즉, 모니터링되는 출력 신호는 실제로 입력 트랜지스터의 수집기에서의 전압이다.그러한 견해는 합법적이지만, 전압 추종자 단계는 피드백 네트워크의 일부가 된다.그것은 피드백의 분석을 더 복잡하게 만든다.

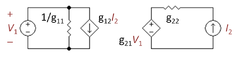
대안적인 견해는 R의₂ 상단의 전압은 출력 트랜지스터의 이미터 전류에 의해 설정된다는 것이다.그러한 견해는 R과₂ R로_f 구성된 완전히 수동적인 피드백 네트워크로 이어진다.피드백을 제어하는 변수는 이미터 전류이므로 피드백은 전류 제어 전류 소스(CCCS)이다.우리는 네 개의 이용 가능한 2포트 네트워크를 통해 검색하고 CCCS가 있는 유일한 것이 그림 4에 나온 g-모수 2포트라는 것을 발견한다.다음 과제는 그림 4의 2-포트(port_f)가 R과₂ R로 구성된 L-섹션과 전기적으로 등가하도록 g-parameter를 선택하는 것이다.이 선택은 두 개의 개별 사례, 즉 두 포트 우측의 VCVS를 단락 회로로 만드는 V₁ = 0의 경우와 왼쪽의 CCCS를 개방 회로로 만드는 I₂ = 0의 경우를 가장 단순하게 살펴서 이루어지는 대수적 절차다.이 두 경우에서의 대수학은 간단하며, 모든 변수를 한 번에 해결하는 것보다 훨씬 쉽다.2-포트 및 L-섹션의 동작을 동일하게 하는 g-parameter의 선택은 아래 표에 나와 있다.

g11	g12	g21	g22
${\displaystyle {\frac {1}{R_{\mathrm {f}}+R_{2}}:$	${\displaystyle -{\frac {R_{2}}:{R_{2}+R_{\mathrm{f}}}}}}}}}}$	${\displaystyle {\frac {R_{2}}:{R_{2}+R_{\mathrm{f}}}}}}}}}}$	${\displaystyle R_{2}/R_{\mathrm {f}\ }$

소신호 회로

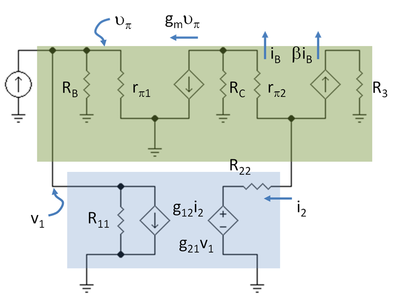
다음 단계는 트랜지스터용 하이브리드 파이 모델을 사용하여 2포트(two-port)를 제자리에 둔 앰프에 대한 작은 신호 도식을 그리는 것이다.그림 5는 표기법₃ R = R_C2 // R_L 및₁₁ R = 1 / g₁₁, R₂₂ = g로₂₂ 도식을 나타낸다.

로드된 오픈 루프 게인

그림 3은 출력 노드를 나타내지만 출력 변수의 선택은 아니다.유용한 선택은 앰프의 단락 전류 출력(단락 전류 이득으로 이어짐)이다.이 변수는 단순히 다른 선택 사항(예: 부하 전압 또는 부하 전류)으로 이어지기 때문에 단락 전류 이득은 아래에서 확인할 수 있다.

먼저 로드된 오픈 루프 게인이 발견된다.피드백은₁₂ g = g = 0을₂₁ 설정하여 꺼진다.피드백이 꺼진 상태에서 스스로 피드백 네트워크의 저항기 때문에 앰프 이득이 얼마나 달라지는지 알아보는 것이다.이₁₁₁ 계산은_B R, R, r_π1 모두 평행이고 v = v_π. 렛₁ R = R₁₁ // R_B // r_π1. 게다가 i₂ = - (β+1) i_B.개방 루프 전류 게인 A의_OL 결과는 다음과 같다.

${\displaystyle A_{\mathrm {OL} }={\frac {\beta i_{\mathrm {B} }}{i_{\mathrm {S} }}}=g_{m}R_{\mathrm {C} }\left({\frac {\beta }{\beta +1}}\right)\left({\frac {R_{1}}{R_{22}+{\frac {r_{\pi 2}+R_{\mathrm {C} }}{\beta +1}}}}\right)\ .}$

피드백으로 이득

피드백에 대한 고전적 접근방식에서 VCVS로 대표되는 피드포워드(g₂₁ v₁)는 무시된다.^[35]이렇게 하면 그림 5의 회로가 그림 1의 블록도를 닮아 피드백이 있는 이득은 다음과 같다.

${\displaystyle A_{\mathrm {FB}}={\frac {A_{\mathrm {OL}}}}{1+{\beta }_{\mathrm {FB}}}}}}}}}}}}}}{\mathrmathrm {OL}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

${\displaystyle A_{\mathrm {FB}}={\frac {A_{\mathrm {OL}}}{1+{{R_{2}}:{R_{2}+R_{\mathrm{f}}}}}}}}},}$

여기서 피드백 계수 β_FB = -g₁₂.트랜지스터 β와 구별하기 위해 피드백 계수에 대해 표기법 β가_FB 도입된다.

입력 및 출력 저항

피드백은 신호원을 부하와 더 잘 일치시키기 위해 사용된다.예를 들어 저항 부하에 전압 소스를 직접 연결하면 전압 분할로 인한 신호 손실이 발생할 수 있지만, 음의 피드백 앰프를 간섭하면 소스가 보이는 겉보기 부하를 증가시킬 수 있고, 부하에 의해 보이는 명백한 드라이버 임피던스를 감소시켜 전압 분할에 의한 신호 감쇠를 피할 수 있다.이 장점은 전압 증폭기로 국한되지 않지만 전류 증폭기, 전도성 증폭기 및 내전성 증폭기에 대해서는 유사하게 매칭 개선이 배치될 수 있다.

임피던스에 대한 피드백의 이러한 효과를 설명하려면 먼저 2포트 이론이 저항 결정에 접근하는 방법에 대한 추론을 한 다음, 그 이론이 가까이에 있는 증폭기에 적용해야 한다.

저항 결정에 대한 배경

그림 6은 피드백 전압 증폭기(왼쪽)의 입력 저항과 피드백 전류 증폭기(오른쪽)의 입력 저항을 찾기 위한 동등한 회로를 보여준다.이러한 배열은 전형적인 밀러 정리 적용이다.

전압 증폭기의 경우, 피드백 네트워크의 출력 전압 βV가_out 직렬로 적용되며, 루프 상으로 이동하는 입력 전압_x V에 반대 극성을 가한다(그러나 지면에 대해서는 극성이 동일하다).그 결과, 증폭기 입력 저항_in R을 통한 유효 전압과 전류가 감소하여 회로 입력 저항이 증가하게 된다(R이_in 분명히 증가한다고 말할 수 있다).그것의 새로운 값은 밀러 정리(전압의 경우)나 기본 회로 법칙을 적용하여 계산할 수 있다.따라서 Kirchhoff의 전압 법칙은 다음을 제공한다.

${\displaystyle V_{x}=I_{x}R_{\mathrm {in}+\beta v_{\mathrm {out}\,}$

여기서 v_out = A_v v_in = A_v I R_xin. 이 결과를 위의 방정식으로 대체하고 피드백 증폭기의 입력 저항성에 대한 해결은 다음과 같다.

${\displaystyle R_{\mathrm {in}}}(fb)={\frac {V_{x}}{{x}}}{{\fracI_{x}}=\왼쪽(1+\베타 A_{v}\오른쪽)R_{\mathrm {in}\ .}$

이 예와 출력 저항 사례에서 나온 일반적인 결론은 다음과 같다: 입력(출력)에서 직렬 피드백 연결은 입력(출력) 저항을 인자(1 + β A )만큼 증가시킨다_OL. 여기서 A_OL = 개방 루프 게인이다.

한편, 전류 증폭기의 경우, 피드백 네트워크의 출력 전류 βI가_out 입력 전류 I과_x 반대 방향으로 병렬로 적용된다.그 결과 회로 입력을 통해 흐르는 총 전류(입력 저항_in R을 통해서만 흐르는 것이 아니라)가 증가하고 그 전체 전압은 감소하여 회로 입력 저항이 감소한다(R은_in 분명히 감소한다).그것의 새로운 값은 이중 밀러 정리(전류용) 또는 기본 키르흐호프의 법칙을 적용하여 계산할 수 있다.

${\displaystyle I_{x}={\frac {V_{\mathrm {in}}}}}{R_{\mathrm {in}}}}}}}}}+\beta i_{\mathrmatrm {out}\ .}$

여기서 i_out = A_i i_in = A_i V_x / R_in. 이 결과를 위의 방정식으로 대체하고 피드백 증폭기의 입력 저항성에 대한 해결은 다음과 같다.

${\displaystyle R_{\mathrm {in}}}(fb)={\frac {V_{x}}{{x}}}{{\fracI_{x}}={\frac {R_{\mathrm{in}}}}}}{{\좌측(1+\beta A_{i}\오른쪽)}}}\.}$

이 예와 출력 저항 사례에 대한 유사한 예에서 일반적인 결론은 다음과 같다: 입력(출력)에서 병렬 피드백 연결이 입력(출력) 저항을 인자(1 + β A_OL )만큼 감소시킨다. 여기서 A_OL = 개방 루프 게인이다.

이러한 결론은 임의 Norton 또는 Thévenin 드라이브, 임의 부하 및 일반 2포트 피드백 네트워크로 사례를 처리하기 위해 일반화할 수 있다.그러나 결과는 2-포트(two-port)로 표현되는 메인 앰프에 따라 달라진다. 즉, 결과는 입력 단자를 드나드는 동일한 전류에 따라 달라지며, 마찬가지로 하나의 출력 단자를 떠나는 동일한 전류도 다른 출력 단자에 들어가야 한다.

정량적 세부사항과 무관하게 더 넓은 결론은 피드백이 입력과 출력 임피던스를 증가시키거나 감소시키는 데 사용될 수 있다는 것이다.

예제 증폭기에 적용

이 저항 결과는 이제 그림 3과 그림 5의 증폭기에 적용된다.게인을 감소시키는 개선계수, 즉 (1 + β_FB A_OL)는 앰프의 입력과 출력 저항성에 대한 피드백의 영향을 직접적으로 결정한다.션트 연결의 경우 입력 임피던스가 이 인자에 의해 감소하고 직렬 연결의 경우 임피던스에 이 인자를 곱한다.그러나 피드백에 의해 수정된 임피던스는 피드백이 꺼진 그림 5의 앰프의 임피던스이며, 피드백 네트워크의 저항기에 의해 발생하는 임피던스에 대한 수정을 포함한다.

따라서 피드백이 꺼진 상태에서 소스가 보는 입력 임피던스는 R_in = R = R₁₁₁ // R_B // r이며_π1, 피드백이 켜진 상태(단, 피드포워드 없음)

${\displaystyle R_{\mathrm {in} }={\frac {R_{1}{1}{1+{\beta }_{\mathrm {FB}{}}{}A_{\mathrmatrm {OL}}}},},}$

여기서 입력 연결이 션트(shunt)이기 때문에 분할이 사용된다. 피드백 2포트는 앰프의 입력 측에 있는 신호 소스와 병렬로 있다.주의사항:A는_OL 피드백 네트워크의 저항기에 의해 수정된, 위에서 발견된 로드된 개방 루프 이득이다.

부하에 의해 보이는 임피던스는 더 많은 논의가 필요하다.그림 5의 부하는 출력 트랜지스터의 수집기와 연결되므로 출력 전류 소스의 무한 임피던스에 의해 증폭기의 본체로부터 분리된다.따라서 피드백은 그림 3의 부하 저항기 R에_L 의해 보이는 것처럼 단순하게 R로_C2 유지되는 출력 임피던스에 영향을 미치지 않는다.^[36][37]

대신에 피드백 네트워크에 연결된 직렬인 출력 트랜지스터(수집기 대신)의 이미터에 표시되는 임피던스를 찾으려면 피드백이 개선 계수(1 + β_FB A_OL)에 의해 이 저항을 증가시킬 것이다.^[38]

부하 전압 및 부하 전류

위에서 도출된 게인은 출력 트랜지스터의 수집기에서 전류 게인이다.전압이 앰프의 출력일 때 이 게인을 게인과 연관시키려면_L 로드 R의 출력 전압이 옴의 법칙에 의해_L v = i_C2(R_C R_L)로 수집기 전류와 관련이 있음을 주목하십시오.결과적으로, 전저항 이득 v_L / i는_S 전류 이득에 R R:를_C2L 곱하여 발견된다.

${\displaystyle {\frac {v_{\mathrm {L}}}}{{\mathrm {FB}}}}}=A_{\mathrm {FB}}}(R_{\mathrm {C2})\parallel R_{\mathrmatrmatrm {L}\}\}\}}.}.}.}.}}.}.}.}.}$

마찬가지로 증폭기의 출력을 부하 저항기 R의_L 전류로 가져간다면 전류 분할은 부하 전류를 결정하고 이득은 다음과 같다.

${\displaystyle {\frac {i_{\mathrm {L} }}{i_{\mathrm {S} }}}=A_{\mathrm {FB} }{\frac {R_{\mathrm {C2} }}{R_{\mathrm {C2} }+R_{\mathrm {L} }}}\ .}$

메인 앰프 블록이 2포트인가?

주의 깊은 독자를 위한 2포트 접근법의 일부 단점이 뒤따른다.

그림 7은 주 증폭기와 피드백 2포트 음영 박스로 된 작은 신호 도식을 보여준다.피드백 2-포트는 포트 조건을 만족시킨다: 입력 포트에서 나는 포트를_in 출입하고, 출력에서와 마찬가지로 출입한다_out.

메인 앰프 블록도 2포트인가?메인 앰프는 상단 음영 박스에 표시된다.접지 연결부에는 라벨이 붙어 있다.그림 7은 그러한 일이 일어나도록 접지 연결을 선택하지 않는 한 주 증폭기가 입력과 출력에서 좌현 조건을 만족시키지 못한다는 흥미로운 사실을 보여준다.예를 들어 입력 측에서 메인 앰프로 들어가는 전류는 I이다_S.이 전류는 피드백 네트워크, 바이어스 저항기_B R 및 입력 트랜지스터 r의_π 베이스 저항의 세 가지 방법으로 나뉜다.주 증폭기의 좌현 조건을 만족시키려면 세 가지 구성 요소 모두를 주 증폭기의 입력 측에 반환해야 하는데, 이는 이미터₁ 리드 G뿐만_E1 아니라 모든 접지 리드가 연결되어야 함을 의미한다. 마찬가지로 출력 측에서도 모든 접지 연결부₂ G와 접지 연결부_E2 G가 연결되어야 한다.그런 다음, 도식도 하단의 피드백 2포트 아래 및 앰프 블록 외부에 있는₁ G를 G에₂ 연결한다.그것은 계획대로 입력면과 출력면 사이를 지류 전류가 갈라지게 한다.이 연결 배열은 입력 트랜지스터의 이미터를 베이스 측 및 컬렉터 측으로 분할한다는 점에 유의하십시오. 이는 물리적으로 불가능하지만 전기적으로 회로는 모든 접지 연결을 하나의 노드로 간주하므로 이 픽션이 허용된다.

물론 그라운드 리드가 연결되는 방식은 앰프(모두 하나의 노드)와 차이가 없지만, 포트 조건과는 차이가 있다.이러한 인공성은 이 접근방식의 약점이다: 방법을 정당화하기 위해 항만 조건이 필요하지만, 회로는 실제로 접지 연결부 사이에서 전류가 거래되는 방식에 영향을 받지 않는다.

그러나 가능한 접지 조건의 배열이 좌현 상태로 이어지지 않으면 회로가 같은 방식으로 동작하지 않을 수 있다.^[39]입력 및 출력 임피던스 결정을 위한 개선 계수(1 + β_FB A_OL)가 작동하지 않을 수 있다.^[40]이 상황은 어색하다. 왜냐하면 투포트를 만들지 못하면 진짜 문제가 반영되거나(그냥 불가능), 상상력의 부족을 반영할 수 있기 때문이다(예를 들어, 이미터 노드를 둘로 분할할 생각은 하지 않았다).결과적으로 포트 조건이 의심될 때 개선 요인이 정확한지 여부를 확인하기 위해 최소 두 가지 접근법이 가능하다. 즉, Spicate를 사용하여 예를 시뮬레이션하고 개선 인자의 사용과 결과를 비교하거나, 시험 선원을 사용하여 임피던스를 계산하고 결과를 비교한다.

보다 현실적인 선택은 2포트 접근방식을 아예 버리고, 로젠스타크 방식, 초마 방식, 블랙먼의 정리 사용 등 신호 흐름 그래프 이론에 근거한 다양한 대안을 사용하는 것이다.^[41]소형 신호 장치 모델이 복잡하거나 사용할 수 없는 경우(예: 장치는 아마도 측정 또는 SPICE 시뮬레이션에서 수치상으로만 알려져 있다) 그러한 선택은 권장될 수 있다.

피드백 증폭기 공식

피드백의 2포트 분석을 요약하면, 이 공식 표를 얻을 수 있다.^[34]

피드백 증폭기	소스 신호	출력 신호	전송 함수	입력 저항	출력 저항
직렬 션트(전압 증폭기)	전압	전압	${\displaystyle A_{vf}={\frac {V_{o}}{V_{i}}}={\frac {A_{v}}}{1+\beta_{v}}}}}}}}}}}}}}}$	${\displaystyle R_{i}(1+\beta _{v}A_{v}}}}$	${\displaystyle {\frac {R_{o}{1+\beta _{v}}}}}$
션트 시리즈(전류 증폭기)	현재	현재	${\displaystyle A_{if}={\frac {I_{o}}}{{}}}{{\fracI_{i}}={\frac {A_{i}}{1+\베타 _{i}A_{i}}}}$	${\displaystyle {\frac {R_{i}}{1+\beta _{i}A_{i}}}}$	${\displaystyle R_{o}(1+\beta _{i})A_{i}}}$
직렬(전송 증폭기)	전압	현재	${\displaystyle A_{gf}={\frac {I_{o}}{V_{i}}}={\frac {A_{g}}{1+\beta_{z}}A_{g}}}}$	${\displaystyle R_{i}(1+\beta _{z})A_{g}}}$	${\displaystyle R_{o}(1+\beta _{z})A_{g}}}$
션트-션트(저항 증폭기)	현재	전압	${\displaystyle A_{zf}={\frac {V_{o}}}{{}}}{{}}}}{{\fracI_{i}}={\frac {A_{z}}{1+\beta _{g}A_{z}}}}}}}}$	${\displaystyle {\frac {R_{i}{1+\beta _{g}A_{z}}}}}}$	${\displaystyle {\frac {R_{o}}{1+\beta _{g}A_{z}}}}}}$

변수와 그 의미는

${\displaystyle A}$ ${\displaystyle A}$- $게인{\displaystyle }$, I ${\displaystyle I}$- 전류, $V{\displaystyle }$ ${\displaystyle V}$- 전압, ${\displaystyle }$ ${\displaystyle \beta }$- 피드백 게인 및 $R{\displaystyle }$ ${\displaysty R}$- 저항.

첨자와 그 의미는

${\displaystyle f}$ ${\displaystyle f}$- 피드백 앰프, ${\displaystyle }$ ${\displaystyle v}$- 전압, g ${\displaystyle g}$- $트랜스듀턴스{\displaystyle }$, Z ${\displaystyle Z}$- 저항, $o{\displaystyle }$ ${\$$displaysty$ $o$$}$- 출력 전류 $및{\displaystyle }$ i$$${\$$displaystystyle$i$\}$ - 저항 입력

예를 들어 $A{\displaystyle {}_{}}$ ${\displaystyle v_{}}$ ${\displaystyle f_{}}$ ${\$는 전압 피드백 증폭기 게인을 의미한다$$.^[34]

왜곡.

공통 이미터 구성과 같은 단순 증폭기는 주로 2차 및 3차 고조파와 같은 저차 왜곡이 있다.오디오 시스템에서는 음악적 신호는 일반적으로 이미 고조파 계열이고, 인간 청각 시스템의 마스킹 효과에 의해 저차 왜곡 제품이 숨겨지기 때문에 이러한 것들은 최소로 들을 수 있다.^[42][43]

음의 피드백(10–15dB)을 적당량 적용한 후 저차 고조파는 줄이지만 고차 고조파가 도입된다.^[44]이것들 또한 가면을 쓰지 않기 때문에, 전체적인 THD가 내려갈 수 있음에도 불구하고 왜곡은 들을 수 없을 정도로 더 심해진다.^[44]이는 오디오 앰프에서 부정적인 피드백이 해롭다는 지속적인 신화로 이어져 ^[45]오디오 애호가 제조사들이 자신의 앰프를 '제로 피드백'(각 단계를 선형화하기 위해 국소 피드백을 사용하는 경우에도)으로 마케팅하도록 이끌고 있다.^[46][47]

그러나 부정적인 피드백의 양이 더욱 증가함에 따라 모든 고조파들이 감소하여 왜곡을 무청각으로 되돌린 다음 원래의 제로피드백 단계 이상으로 개선한다(시스템이 엄격히 안정되어 있다고 가정한다).^[48][45][49]그래서 문제는 부정적인 피드백이 아니라 부족한 양이다.

참고 항목

• 점증상 이득 모형
• 블랙맨 정리
• 복음도
• 버퍼 앰프가 음의 피드백이 있는 기본 작동 앰프 증폭 단계를 고려함
• 공통 컬렉터(이미터 팔로워)는 기본 트랜지스터 증폭 단계 전용이며, 음의 피드백이 있음
• 여분요소정리
• 주파수 보상
• 밀러 정리는 음의 피드백 회로의 입출력 임피던스를 결정하는 강력한 도구다.
• 기본 OP 앰프 및 인버팅 앰프를 제공하는 작동 앰프
• 작동 증폭기 애플리케이션은 음성 피드백이 있는 가장 일반적인 작동 전류 회로를 표시함
• 위상 여유
• 극분할
• 수익률
• 스텝 응답

참조 및 참고 사항