파크스-매클렐런 필터 설계 알고리즘
Parks–McClellan filter design algorithm이 문서는 신호 처리 전문가의 주의가 필요합니다.자세한 내용은 토크 페이지를 참조하십시오.(2014년 7월) |
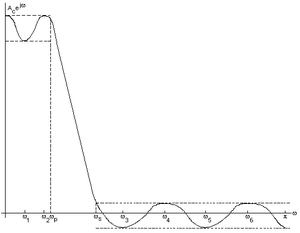
y축은 주파수 응답 H(θ)이고 x축은 다양한 라디안 주파수 θ입니다i.X축에 표시된 2개의 주파수 and와pp ω는s 통과 대역 컷오프 주파수, indicates는s 정지 대역 컷오프 주파수임을 알 수 있습니다.왼쪽 상단의 리플라이크 플롯은 패스 밴드 리플, 오른쪽 하단의 리플은 스톱 밴드 리플입니다.그래프 왼쪽 상단에 있는 두 개의 점선은 and를p 나타내고 오른쪽 하단에 있는 두 개의 점선은 δ을s 나타냅니다.나열된 다른 모든 주파수는 주파수 응답도의 극한 주파수를 나타냅니다.그 결과, 6개의 극단 주파수가 존재하며, 다음으로 통과 대역과 정지 대역 주파수를 추가하여 플롯에 총 8개의 극단 주파수를 부여합니다.
1972년 James McClelan과 Thomas Parks가 발표한 Parks-Mclelan 알고리즘은 최적의 체비셰프 유한 임펄스 응답(FIR) 필터를 찾기 위한 반복 알고리즘이다.Parks – McClelan 알고리즘은 효율적이고 최적의 FIR 필터를 설계 및 구현하기 위해 사용됩니다.또한 최적의 필터 계수를 찾기 위해 간접적인 방법을 사용합니다.
알고리즘의 목적은 체비셰프 근사치를 활용하여 통과 대역과 정지 대역의 오류를 최소화하는 것입니다.Parks-McClelan 알고리즘은 Remez 교환 알고리즘의 변형으로 FIR 필터용으로 특별히 설계되어 있습니다.FIR 필터 설계의 표준 방법이 되었습니다.
최적의 FIR 필터 설계 이력
1960년대에 아날로그 필터 설계 분야의 연구자들은 필터 설계를 위해 체비셰프 근사치를 사용하고 있었다.이 기간 동안, 최선의 필터는 주파수 응답 크기에 등가리플 특성을 포함하며 타원 필터(또는 코어 필터)는 체비셰프 근사치와 관련하여 최적이라는 것이 잘 알려져 있었다.1960년대에 디지털 필터 혁명이 시작되었을 때, 연구원들은 무한 임펄스 응답(IIR) 디지털 타원형 필터를 만들기 위해 쌍선형 변환을 사용했습니다.그들은 또한 동일한 필터링 작업을 수행하기 위한 FIR 필터 설계의 가능성을 인식했고 곧 체비셰프 [1]근사치를 사용하여 최적의 FIR 필터를 검색하기 시작했다.
수학과 공학에서는 최적의 반응이 등치 거동을 나타내며 파문의 수는 체비셰프 근사치를 사용하여 셀 수 있다는 것이 잘 알려져 있었다.최적의 체비셰프 FIR 필터를 위한 설계 프로그램을 제작하기 위한 여러 시도가 1962년과 [1]1971년 사이에 수행되었다.수많은 시도에도 불구하고 대부분은 알고리즘 구현 또는 문제 공식의 문제로 인해 성공하지 못했습니다.예를 들어, Otto Herrmann은 제한된 밴드 [1]가장자리로 등가필터를 설계하는 방법을 제안했다.이 방법은 일련의 비선형 방정식을 풀어서 최대 리플 수로 등가 주파수 응답을 얻었습니다.당시 도입된 또 다른 방법은 최적의 체비셰프 근사치를 구현했지만 알고리즘은 상대적으로 낮은 차수의 [1]필터 설계로 제한되었다.
Herrmann의 방법과 유사하게 Ed Hofstetter는 FIR 필터를 가능한 한 많은 리플로 설계하는 알고리즘을 제시했습니다.이것은 Maximal Riple 알고리즘이라고 불리게 되었습니다.Maximal Ripple 알고리즘은 보간을 통해 교대 오차 조건을 부과하고 교대 솔루션이 만족해야 [1]하는 일련의 방정식을 해결했습니다.Maximal Riple 알고리즘의 한 가지 주목할 만한 제한 사항은 밴드 에지가 설계 절차의 입력으로 지정되지 않았다는 것입니다.오히려 초기 주파수 세트i {θ}와 원하는 함수 Di(θ)가 암묵적으로 통과 및 정지 대역을 정의했습니다.최적의 필터를 설계하려는 이전 시도와 달리 Maximal Riple 알고리즘은 최적의 필터가 [1]있는 주파수 집합 {θi}을(를) 찾으려는 교환 방법을 사용했습니다.따라서 Maximal Ripple 알고리즘은 최적의 필터 설계는 아니었지만 Parks-McClelan 알고리즘이 어떻게 공식화할지에 상당한 영향을 미쳤다.
역사
1970년 8월, 제임스 맥클렐런은, 아날로그 필터 디자인의 수학적 모델에 집중해 라이스 대학의 대학원에 입학해, 필터 [1]디자인에 대한 관심으로 「디지털 필터」라고 불리는 새로운 코스에 등록했습니다.이 과정은 Thomas Parks와 Sid Burrus가 공동으로 가르쳤다.그 당시 DSP는 새로운 분야였고 그 결과 강의는 최근 발표된 연구 논문과 관련된 경우가 많았다.1971년 봄, 다음 학기에 토마스 파크스는 "신호론"이라고 불리는 강좌를 개설했고, 매클렐런도 [1]이 강좌를 들었다.이번 학기 봄 방학 동안 파크스는 회의에 참석하기 위해 휴스턴에서 프린스턴으로 차를 몰고 갔습니다.그 곳에서 Ed Hofstetter는 새로운 FIR 필터 설계 알고리즘(Maximal Ripple 알고리즘)에 대한 프레젠테이션을 들었습니다.Hofstetter, Oppenheim 및 Siegel의 논문을 휴스턴으로 가져와 체비셰프 근사 이론을 사용하여 FIR [1]필터를 설계할 가능성에 대해 생각했습니다.그는 Hofstetter의 알고리즘에 구현된 방법이 Remez 교환 알고리즘과 유사하다는 것을 듣고 Remez 교환 알고리즘을 사용하는 경로를 추구하기로 결정했다."신호가론" 코스의 학생들은 프로젝트를 해야 했고 체비셰프 근사가 코스의 주요 주제였기 때문에 이 새로운 알고리즘의 구현은 제임스 맥클렐런의 코스 프로젝트가 되었습니다.이는 결국 최적의 체비셰프 근사 이론과 효율적인 구현이 포함된 파크-매클렐란 알고리즘으로 이어졌다.봄 학기가 끝날 무렵, McClelan과 Parks는 FIR 필터의 Remez 교환 알고리즘의 변형을 작성하려고 했습니다.개발에는 약 6주가 걸렸고 5월 말까지 최적의 필터가 성공적으로 설계되었다.
알고리즘
Parks – McClelan 알고리즘은 다음 [1]단계를 사용하여 구현됩니다.
- 초기화:최대 주파수i(0) 집합 { of}을(를) 선택하십시오.
- 유한 집합 근사:현재 극단 집합에서 최량 체비셰프 근사치를 계산하여 현재 극단 집합에서 최소-최대 오류 값 θ를(m) 제공합니다.
- 보간:(2)를 사용하여 주파수 δ 세트 전체에 걸쳐 오차 함수 E(ω)를 계산합니다.
- 세트 δ에서 로컬 최대값(m) E())를 찾습니다.
- max(ω∈Ω)(m)(m) E()) > , 、 E())의 로컬 최대값이 있는 새로운 주파수를(m) 선택하여 극단값 세트를 {}}(으i(m+1))로 업데이트합니다.(4) 및 (5)에 설명된 대로 순서가 지정된 주파수 집합에서 오류가 번갈아 발생하는지 확인합니다.스텝 2로 돌아가서 반복합니다.
- max(m) E(')가(m) 「」이면(ω∈Ω), 알고리즘은 완료됩니다.집합 {θi(0)}과(와) 보간식을 사용하여 역 이산 푸리에 변환을 계산하여 필터 계수를 구합니다.
파크스-매클렐런 알고리즘은 다음과 [2]같이 재작성할 수 있다.
- L+2 극단 주파수를 최초로 추측합니다.
- 주어진 방정식을 사용하여 using를 계산합니다.
- 라그랑주 보간법을 사용하여 통과 대역과 정지 대역을 통해 A())의 고밀도 샘플 세트를 계산한다.
- 새로운 L+2 최대 극단값을 확인합니다.
- 교대 정리가 만족되지 않으면 (2)로 돌아가서 교대 정리가 만족될 때까지 반복한다.
- 만약 교대 정리가 만족된다면, 우리는 h(n)를 계산하고 우리는 끝난다.
위의 Parks-Mclelan 알고리즘에 대한 기본적인 이해를 얻으려면 위의 알고리즘을 다음과 같이 간단한 형태로 다시 쓸 수 있습니다.
- 익스트림의 위치는 패스와 스톱 밴드에서 균등하게 간격을 두고 있는 것 같습니다.
- 다항식 보간을 수행하고 국소 극단의 위치를 다시 추정합니다.
- 극단을 새로운 위치로 이동하고 극단의 이동이 멈출 때까지 반복합니다.
설명.
오른쪽 위의 그림은 표시된 플롯의 다양한 극단 주파수를 보여줍니다.극한 주파수는 정지 및 통과 대역의 최대 및 최소 지점입니다.정지 대역 리플은 플롯의 오른쪽 하단에 있는 리플의 아래쪽 부분이고 통과 대역 리플은 플롯의 왼쪽 상단에 있는 리플의 위쪽 부분입니다.그래프를 가로지르는 점선은 or 또는 최대 오차를 나타냅니다.극한 주파수의 위치에 따라 최적 δ 또는 최적 오차에 대한 공식이 있습니다.첫 번째 시도에서는 최적의 θ나 극단의 정확한 위치를 알 수 없기 때문에 반복한다.실제로 처음에 극단의 위치를 가정하여 θ를 계산한다.그런 다음 극단값을 재추정하여 이동하여 ,, 즉 오류를 재계산합니다.「」의 변경이 정지할 때까지, 이 프로세스를 반복합니다.이 알고리즘에 의해 일반적으로 10~12회 반복하여 [3]δ 오류가 수렴됩니다.
기타 주의사항
체비셰프 근사치를 적용하기 전에 일련의 단계가 필요했다.
- 근사치에 대한 기저 함수 집합을 정의한다.
- 대역통과 필터의 통과 대역과 정지 대역은 항상 전이 [1]영역에 의해 분리된다는 사실을 이용하십시오.
FIR 필터는 코사인 케이스의 합계로 줄일 수 있기 때문에 가능한 모든 선형 위상 FIR 필터를 실행하기 위해 동일한 코어 프로그램을 사용할 수 있습니다.Maximum Ripple 접근 방식과 달리 이제 밴드 에지를 미리 지정할 수 있습니다.
Parks-McClelan 알고리즘을 사용하여 최적의 필터 설계를 효율적으로 구현하려면 다음 두 가지 어려움을 극복해야 합니다.
- 유연한 교환 전략의 정의
- 견고한 보간법 [1]구현.
어떤 의미에서 프로그래밍에는 FIR 필터 설계에 사용되는 알려진 알고리즘의 구현과 적응이 수반되었습니다.교환 전략의 두 가지 측면은 프로그램을 보다 효율적으로 만들기 위해 채택되었습니다.
- 통과 대역과 정지 대역 사이의 극한 주파수 할당
- 프로그램이 [1]반복될 때 밴드 간의 극단 이동을 활성화합니다.
초기화 시 통과 대역과 정지 대역의 극단 수는 대역 크기 비율을 사용하여 할당할 수 있습니다.게다가, 통과 및 정지 대역 에지는 항상 극한 세트에 배치되며, 프로그램의 로직은 그러한 에지 주파수를 극한 세트에 유지합니다.대역 간 이동은 모든 후보 극단 주파수에서 오차 크기를 비교하고 가장 큰 값을 취함으로써 제어되었다.알고리즘의 두 번째 요소는 오류 함수를 평가하는 데 필요한 보간 단계입니다.그들은 라그랑주 보간법의 중심적 형태라고 불리는 방법을 사용했는데, 그것은 매우 강력했다.
파크스-매클렐런 알고리즘의 모든 조건은 체비셰프의 교대 정리에 기초한다.교대 정리는 최대 오차를 최소화하는 L차 다항식이 최소 L+2 극단값을 가질 것이라고 말한다.최적의 주파수 응답은 최대 리플 [3]경계에 거의 도달하지 않습니다.극단점은 통과 및 정지 밴드 가장자리와 =0 또는 =0 또는 둘 다에서 발생해야 합니다.차수 L의 다항식의 도함수는 차수 L-1의 다항식으로, 차수 L-1은 [3]최대 0이 될 수 있다.따라서 국소 극단의 최대 수는 L-1 국소 극단에 4개의 띠 가장자리를 더한 것으로, 총 L+3 극단이 됩니다.
레퍼런스
- ^ a b c d e f g h i j k l m McClellan, J.H.; Parks, T.W. (2005). "A personal history of the Parks-Mc Clellan algorithm". IEEE Signal Processing Magazine. 22 (2): 82–86. Bibcode:2005ISPM...22...82M. doi:10.1109/MSP.2005.1406492.
- ^ Jones, Douglas (2007), Parks–McClellan FIR Filter Design, retrieved 2009-03-29
- ^ a b c Lovell, Brian (2003), Parks–McClellan Method (PDF), retrieved 2009-03-30
기타 참고 자료
다음 추가 링크는 Parks-Mclelan 알고리즘과 James McClelan 및 Thomas Parks가 작성한 기타 연구 및 논문에 대한 정보를 제공합니다.
- 선형 위상이 있는 비재귀 디지털 필터에 대한 체비셰프 근사
- MATLAB를 사용한 FIR 로우패스 필터의 파크 – McClelan 설계에 대한 간단한 도움말
- DSP의 개요
- MathWorks MATLAB 문서
- ELEC4600 강의 노트 (원래 링크, 2012년 4월 15일 아카이브)
- C코드 실장 (LGPL 라이선스)– 제이크 야노베츠 지음
- Iowa Hills Software. "Example C Code". Retrieved 3 May 2014.
- 개정 및 확장된 알고리즘 McClelan, Parks, & Rabiner, 1975; Fortran 코드.


