위상장 모형

위상장 모델은 계면 문제를 해결하기 위한 수학적 모델입니다.주로 고체화 역학에 적용되어 왔지만 점성 ^[1]운지,^[2] 파괴 역학,^[3]^[4]^[5]^[6] 수소 취성, ^[7]소포 역학 등 다른 분야에도 적용되어 왔습니다.^[8]^[9]^[10]^[11]

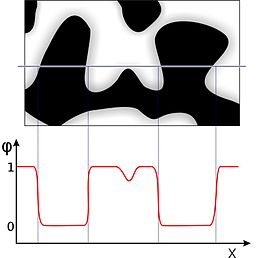
방법은 순서 매개 변수 역할을 하는 보조 필드(위상 필드)의 진화를 위해 계면의 경계 조건을 편미분 방정식으로 대체합니다.이 위상 필드는 각 위상에서 두 개의 서로 다른 값(예: +1 및 -1)을 취하며, 인터페이스 주변의 영역에서 두 값 사이에 매끄러운 변화가 발생한 다음 유한 폭으로 확산됩니다.인터페이스의 이산 위치는 위상 필드가 특정 값(예를 들어, 0)을 취하는 모든 포인트의 집합으로 정의될 수 있습니다.

위상장 모델은 일반적으로 극소의 계면 폭의 한계(이른바 날카로운 계면 한계)에서 정확한 계면 역학이 회복되는 방식으로 구성됩니다.이 접근 방식은 전체 시스템에 대한 편미분 방정식 세트를 통합함으로써 문제를 해결할 수 있으므로 인터페이스에서 경계 조건의 명시적인 처리를 피할 수 있습니다.

위상 필드 모델은 Fix와^[12] Langer에 의해 처음 소개되었으며,^[13] 고체화 및 기타 영역에 대한 관심이 증가하고 있습니다.

위상장 모형의 방정식

위상장 모델은 일반적으로 주어진 계면 역학을 재현하기 위해 구성됩니다.예를 들어, 응고 문제에서 전방 역학은 벌크의 농도 또는 온도와 계면의 일부 경계 조건(국소 평형 조건 및 보존 법칙)에 대한 확산 방정식에 의해 주어지는데,^[14] 이는 날카로운 계면 모델을 구성합니다.

위상 필드 모델의 많은 공식은 순서 매개 변수(위상 필드)와 확산 필드(변화형 공식)에 따라 자유 에너지 함수를 기반으로 합니다.그런 다음 일반적인 통계 물리학 관계를 사용하여 모델의 방정식을 얻습니다.이러한 함수는 물리적 고려 사항으로 구성되지만 인터페이스 너비와 관련된 매개 변수 또는 매개 변수 조합을 포함합니다.그런 다음 이 너비가 0이 되는 모델의 한계를 연구하여 이 한계를 의도된 날카로운 인터페이스 모델로 식별할 수 있는 방법으로 모델의 매개 변수를 선택합니다.

다른 공식은 열역학적 함수식(비변형 공식)을 언급하지 않고 위상장 방정식을 직접 작성하는 것으로 시작합니다.이 경우 위상 필드 모델의 작은 인터페이스 폭 제한을 수행할 때 복구해야 한다는 의미에서 유일한 기준은 날카로운 인터페이스 모델입니다.

위상장 방정식은 문제에서 가장 작은 길이 척도에 비해 인터페이스 폭이 작을 때 원칙적으로 인터페이스 역학을 재현합니다.응고 시 이 눈금은 모세관 $d_{o}$ 가 ${\$ 로 $d_{o}$ 미세 눈금입니다.계산적 관점에서 볼 때, 그러한 작은 규모를 해결하는 편미분 방정식의 통합은 금지됩니다.그러나 카르마와 라펠은 이러한 조건을 완화할 수 있도록 허용하고 위상장 모델을 사용하여 실제적인 정량적 시뮬레이션의 길을 열어준 얇은 인터페이스 한계를 도입했습니다.^[15]컴퓨터의 성능이 향상되고 위상장 모델링의 이론적 발전에 따라 위상장 모델은 인터페이스 문제의 수치 시뮬레이션에 유용한 도구가 되었습니다.

변형 제형

위상 필드에 대한 모델은 시스템의 자유 에너지에 대한 명시적인 표현이 있는 경우 물리적 인수에 의해 구성될 수 있습니다.응고 문제에 대한 간단한 예는 다음과 같습니다.

F[e,\varphi ]=\int d{\mathbf {r}}\left[K {\mathbf {\nabla}}\varphi ^{2}+h_{0}f(\varphi)+e_{0}u(\varphi)^{2}\right]

여기서 φ $\varphi$ 은(는) 위상 필드, $u(\varphi )=e/e_{0}+h(\varphi )/2$ φ $u(\varphi )=e/e_{0}+h(\varphi )/2$ = e $u(\varphi )=e/e_{0}+h(\varphi )/2$ / $u(\varphi )=e/e_{0}+h(\varphi )/2$ $u(\varphi )=e/e_{0}+h(\varphi )/2$ + h $u(\varphi )=e/e_{0}+h(\varphi )/2$ φ $u(\varphi )=e/e_{0}+h(\varphi )/2$ ) $u(\varphi )=e/e_{0}+h(\varphi )/2$ / 2 {\ $displaystyle$ u(\ $varphi$ ) $u(\varphi )=e/e_{0}+h(\varphi )/2$ = $e$ / $e_{0}$ + $h(\varphi$ ) / $e$ $u(\varphi )=e/e_{0}+h(\varphi )/2$ e $e$ 은(는) 단위 볼륨당 로컬 $h$ $,$ h {\ $displaystyle h}$ 은(는) φ {\displaystyle \ $varphi }$ 의 특정 다항식 함수, $\varphi$ $e_{0}={L^{2}}/{T_{M}c_{p}}$ $e_{0}={L^{2}}/{T_{M}c_{p}}$ = $e_{0}={L^{2}}/{T_{M}c_{p}}$ 2 $e_{0}={L^{2}}/{T_{M}c_{p}}$ / $e_{0}={L^{2}}/{T_{M}c_{p}}$ M $e_{0}={L^{2}}/{T_{M}c_{p}}$ ${\displaystyle e_{0$ } = { $L^{2}}/{{$ displaystyle e} $T_{M}c_{p}}($ $L$ 서 L $L$ 은 $L$ 잠열, ${\$ 은 $T_{M}$ 용융온도, ${\$ 는 $c_{{p}}$ 비열)입니다.∇ φ가 $\nabla \varphi$ 인 용어는 계면 에너지에 해당합니다.함수 $f(\varphi )$ ( $f(\varphi )$ φ $f(\varphi )$ ) ${\displaystyle$ f $(\varphi )}$ 는 일반적으로 각 단계의 대량의 자유 에너지 밀도를 설명하는 이중 우물 전위로 간주되며, 함수 $f(\varphi )$ ( $f(\varphi )$ φ $f(\varphi )$ ) $f(\varphi )$ 의 두 최소값에 해당합니다 $f(\varphi )$ 상수 $K$ $K$ 및 $K$ $h_{0}$ ${\$ 은 $h_{0}$ 각각 단위 길이당 에너지 및 단위 부피당 에너지 차원을 갖습니다.그런 다음 인터페이스 너비는 $W={\sqrt {K/h_{0}}}$ = $W={\sqrt {K/h_{0}}}$ / $W={\sqrt {K/h_{0}}}$ $W={\sqrt {K/h_{0}}}$ ${\displaystyle$ W = {\ $sqrt {K/h_{0}}}$ 로 지정됩니다 $W={\sqrt {K/h_{0}}}$ 위상 필드 모델은 다음과 같은 변형 관계로부터 얻을 수 있습니다.^[16]

\partial _{t}\varphi =-{\frac {1}{\tau }}\left ({\frac {\delta F}{\delta \varphi}}\right)+\eta({\mathbf {r}},t)

{\displaystyle \partial _{t}e=De_{0}\nabla^{2}\left ({\frac {\delta F}{\delta e}}\right)-{\mathbf {\nabla}}\cdot {\mathbf {q}_{e}(\mathbf {r},t)

여기서 D는 변수 $e$ $e$ 에 대한 확산 계수이고 $e$ η $\eta$ {\ $displaystyle \eta}$ 와 q $\mathbf {q} _{e}$ {\ $displaystyle \mathbf {q}$ _ ${e}$ 는 열 변동을 설명하는 확률적 항입니다(변동 분산 정리에서 통계적 속성을 얻을 수 있습니다).첫 번째 방정식은 위상장의 진화에 대한 방정식을 제공하는 반면, 두 번째 방정식은 확산 방정식으로 일반적으로 온도 또는 (합금의 경우) 농도에 대해 다시 작성됩니다.다음 방정식은 $l$ $l$ 인 공간과 $l$ $l^{2}/D$ / D $l^{2$ / $D}$ 인 시간의 스케일링 공간입니다 $l^{2}/D$

\alpha \varepsilon ^{2}\partial _{t}\varphi =\varepsilon ^{2}\nabla ^{2}\varphi -f'(\varphi )-{\frac {e_{0}}{h_{0}}h'(\varphi )u+{\tilde {\eta}}({\mathbf {r}},t)

\partial _{t}u=\nabla ^{2}u+{\frac {1}{2}}h'(\varphi )\partial _{t}\varphi -\mathbf {\nabla} \cdot \mathbf {q} _{u}(\mathbf {r},t)

여기서 ε = $\varepsilon =W/l$ / l ${\displaystyle \varepsilon$ = W $/l}$ 은(는) 비차원 인터페이스 폭, $\alpha ={D\tau }/{W^{2}h_{0}}$ = $\alpha ={D\tau }/{W^{2}h_{0}}$ τ $\alpha ={D\tau }/{W^{2}h_{0}}$ / $\alpha ={D\tau }/{W^{2}h_{0}}$ 2 $\alpha ={D\tau }/{W^{2}h_{0}}$ $\alpha ={D\tau }/{W^{2}h_{0}}$ ${\displaystyle \alpha$ = { $D\tau}/{W^{2}h_{0}},$ ${\tilde {\eta }}({\mathbf {r} },t)$ η ${\tilde {\eta }}({\mathbf {r} },t)$ t ${\tilde {\eta }}({\mathbf {r} },t)$ ${\displaystyle {\tilde {\eta}}({\mathbf {r}},$ $\mathbf {q} _{u}(\mathbf {r} ,t)$ ( $\mathbf {q} _{u}(\mathbf {r} ,t)$ $\mathbf {q} _{u}(\mathbf {r} ,t)$ $\mathbf {q} _{u}(\mathbf {r}, t)$ 은(는) 비차원 노이즈입니다.

대체 에너지 밀도 함수

자유 에너지 $f(\varphi )$ 인 f $f(\varphi )$ φ $)$ {\ $displaystyle$ f $(\varphi$ 를 선택하면 인터페이스의 물리적 동작에 상당한 영향을 미칠 수 있으므로 주의하여 선택해야 합니다.이중 우물 함수는 임계점 근처의 반데르발스 상태 방정식의 근사치를 나타내며, 위상 필드 모델이 인터페이스 추적 목적으로만 사용될 때 구현의 단순성을 위해 역사적으로 사용되었습니다.그러나 이것은 종종 관찰되는 자발적인 낙하 수축 현상으로 이어졌으며, 임계점 근처의 상태 방정식에 의해 예측된 높은 위상 혼화성은 위상의 상당한 상호 침투를 허용하고 결국 반경이 일부 임계 값 미만인 물방울의 완전한 소멸로 이어질 수 있습니다.^[17]시뮬레이션 기간 동안 감지된 연속성 손실을 최소화하려면 이동성 매개 변수에 대한 제한이 필요하므로 대류로 인한 계면 번짐, 자유 에너지 최소화로 인한 계면 재구성(즉, 이동성 기반 확산) 및 위상 간 침투 사이에서 섬세한 균형이 필요합니다.인터페이스 추적 응용을 위한 대체 에너지 밀도 함수에 대한 최근의 검토는 자발적인 강하 수축 현상과 이동성의 제한을 피하는 이중 장애물 함수의 수정된 형태를 제안했습니다.^[18]비교 결과를 통해 이중 우물 기능과 fluid 볼륨의 날카로운 인터페이스 기술을 사용한 많은 벤치마크 시뮬레이션을 제공합니다.제안된 구현은 이중 우물 함수보다 계산 복잡도가 약간 더 클 뿐이며, 시뮬레이션된 현상의 지속 시간/성질이 위상 연속성 문제(즉, 작은 물방울, 확장 시뮬레이션, 다중 int)를 가져오는 위상 필드 모델의 인터페이스 추적 응용에 유용함을 입증할 수 있습니다.erfaces 등).

위상장 방정식의 날카로운 계면 한계

위상장 모델은 날카로운 인터페이스 모델로 표현되는 주어진 인터페이스 역학을 의도적으로 재현하도록 구성될 수 있습니다.그러한 경우 제안된 위상장 방정식 세트의 날카로운 인터페이스 한계(즉, 인터페이스 폭이 0으로 갈 때의 한계)가 수행되어야 합니다.이 한계는 일반적으로 인터페이스 폭 ε $\varepsilon$ 의 힘으로 모델의 필드를 점근적으로 확장함으로써 얻어집니다 $\varepsilon$ 이 확장은 계면 영역(내부 확장)과 벌크(외부 확장)에서 모두 수행된 후 순서에 따라 점근적으로 일치합니다.결과는 확산장에 대한 편미분 방정식과 인터페이스의 일련의 경계 조건을 제공하며, 이는 날카로운 인터페이스 모델에 해당해야 하며 이를 비교하면 위상 필드 모델의 매개 변수 값을 제공합니다.

이러한 확장이 초기 위상 필드 모델에서 ε $\varepsilon$ 에서만 하위 순서까지 수행된 반면, 최근 모델에서는 원하지 않는 가짜 효과를 취소하거나 새로운 물리학을 모델에 포함하기 위해 고차 점근법(thin interface limit)을 사용합니다.예를 들어, 이 기술은 운동 효과를 취소하고,^[15] 위상에서 확산성이 동일하지 않은 경우를 처리하고,^[19] 점성 운지법과^[2] 2상 나비에를 모델링할 수 있도록 허용했습니다.–Stokes flow,^[20] 모델에 변동을 포함하는 ^[21]등의 작업을 수행합니다.

다상장 모형

다중 위상 필드 모델에서, 마이크로구조는 각각 특정 위상 또는 결정학적 방향과 관련된 순서 파라미터 세트에 의해 설명됩니다.이 모델은 주로 여러 입자가 진화하는 고체 상태 상 변환(예: 철 합금의 오스테나이트에서 페라이트로의 재결정 또는 1차 변환)에 사용됩니다.다중 위상 필드 모델은 미세 구조에서 다중 입자를 설명할 수 있는 것 외에도 특히 기술 합금 등급에서 발생하는 다중 열역학적 위상을 고려할 수 있습니다.^[22]

그래프의 위상 필드 모형

연속체 위상 필드 모델에 대한 많은 결과는 그래프에 대한 개별 유사체를 가지고 있으며, 그래프의 미적분을 미적분으로 대체합니다.

파괴역학에서의 위상장 모델링

고체의 파괴는 종종 이산 또는 확산 균열 표현을 사용하여 유한 요소 맥락 내에서 수치적으로 분석됩니다.유한 요소 표현을 사용하는 접근 방식은 종종 요소 내 수준에 내장된 강력한 불연속성을 사용하며, 종종 스트레스, 변형 에너지 밀도 또는 에너지 방출 속도 또는 균열 경로를 결정하기 위한 가상 균열 폐쇄 기술 및 리메싱과 같은 기타 특수 처리를 기반으로 한 추가 기준이 필요합니다.반면에, 확산 균열 표현을 사용하는 방법은 연속체 손상 모델 및 위상장 파괴 이론과 같은 변위장의 연속성을 유지합니다.후자는 변형된 형태로 그리피스의 원리를 재구성한 것으로 거슬러 올라가며 기울기 강화 손상형 모델과 유사성이 있습니다.파괴에 대한 위상장 접근법의 가장 매력적인 특징은 탄성 에너지와 파괴 에너지를 결합하는 최소화 문제로부터 균열 개시 및 균열 경로가 자동으로 얻어진다는 점일 것입니다.많은 상황에서 균열 핵생성은 안정성을 잃을 때까지 탄성 용액과 관련된 임계점의 분기를 따르는 것으로 적절히 설명될 수 있습니다.특히, 파괴의 위상장 모델은 탄성 변형률 에너지 밀도가 공간적으로 일정할 때에도 핵생성을 허용할 수 있습니다.^[23]이 접근법의 한계는 핵생성이 응력이 아닌 변형 에너지 밀도에 기반한다는 것입니다.이러한 문제를 해결하고자 하는 것은 핵추진력의 도입에 기초한 대안적 관점입니다.^[24]

집합세포이동을 위한 위상장모형

아데노신 삼인산의 소비로 인해 생물학적 세포 그룹은 복잡한 방식으로 자가 추진할 수 있습니다.응집력이나 여러 화학적 단서와 같은 세포들 사이의 상호작용은 조직화된 방식으로 움직임을 만들어낼 수 있는데, 이 현상을 "집단 세포 이동"이라고 합니다.이러한 현상에 대한 이론적 모델은 위상장 모델이며^[25]^[26], 세포종별 위상장과 화학작용제 농도와 같은 추가적인 필드 변수를 포함합니다.그러한 모델은 암, 상처 치유, 형태형성, 외생체 현상과 같은 현상에 사용될 수 있습니다.

소프트웨어

PACE3D – 3D의 Crystal Evolution을 위한 병렬 알고리즘은 다상 다상 다성분 변환, 대규모 결정립 구조 및 유체 흐름, 탄성, 플라스틱 및 자기 상호 작용과의 결합을 포함한 병렬화된 위상 필드 시뮬레이션 패키지입니다.그것은 칼스루에 응용과학대학과 칼스루에 기술연구소에서 개발되었습니다.
MMSP(Mesoscale Microstructure Simulation Project)는 그리드 기반 미세구조 시뮬레이션을 위한 C++ 클래스 모음입니다.
MICRESS(MICResture Evolution Simulation Software)는 열역학 및 운동 데이터베이스에 결합된 다중 구성 요소, 다중 위상 필드 시뮬레이션 패키지입니다.ACCESS e.V에 의해 개발 및 유지 관리됩니다.
아이다호 국립 연구소에서 개발된 위상장 시뮬레이션을 지원하는 MOOSE 대규모 병렬 오픈 소스 C++ 다중 물리학 유한 요소 프레임워크.
PhasePot은 위상 필드 모델과 몬테카를로 포트 모델을 조합하여 사용하는 Windows 기반 마이크로구조 시뮬레이션 도구입니다.
OpenPhase는 다상장 모델을 기반으로 1차 위상 변환이 진행되는 시스템에서 미세구조 형성 시뮬레이션을 위한 오픈소스 소프트웨어입니다.
mef90/vDef는 에서 개발된 이론을 기반으로 한 오픈 소스 변동 위상장 파괴 시뮬레이터입니다.^[3]^[4]^[5]

참고문헌

^ Boettinger, W. J.; Warren, J. A.; Beckermann, C.; Karma, A. (2002). "Phase-Field Simulation of Solidification". Annual Review of Materials Research. 32: 163–194. doi:10.1146/annurev.matsci.32.101901.155803.
^ ^a ^b Folch, R.; Casademunt, J.; Hernández-Machado, A.; Ramírez-Piscina, L. (1999). "Phase-field model for Hele-Shaw flows with arbitrary viscosity contrast. II. Numerical study". Physical Review E. 60 (2): 1734–40. arXiv:cond-mat/9903173. Bibcode:1999PhRvE..60.1734F. doi:10.1103/PhysRevE.60.1734. PMID 11969955. S2CID 8488585.
^ ^a ^b Bourdin, B.; Francfort, G.A.; Marigo, J-J. (April 2000). "Numerical experiments in revisited brittle fracture". Journal of the Mechanics and Physics of Solids. 48 (4): 797–826. Bibcode:2000JMPSo..48..797B. doi:10.1016/S0022-5096(99)00028-9.
^ ^a ^b Bourdin, Blaise (2007). "Numerical implementation of the variational formulation for quasi-static brittle fracture". Interfaces and Free Boundaries: 411–430. doi:10.4171/IFB/171. ISSN 1463-9963.
^ ^a ^b Bourdin, Blaise; Francfort, Gilles A.; Marigo, Jean-Jacques (April 2008). "The Variational Approach to Fracture". Journal of Elasticity. 91 (1–3): 5–148. doi:10.1007/s10659-007-9107-3. ISSN 0374-3535. S2CID 120498253.
^ Karma, Alain; Kessler, David; Levine, Herbert (2001). "Phase-Field Model of Mode III Dynamic Fracture". Physical Review Letters. 87 (4): 045501. arXiv:cond-mat/0105034. Bibcode:2001PhRvL..87d5501K. doi:10.1103/PhysRevLett.87.045501. PMID 11461627. S2CID 42931658.
^ Martinez-Paneda, Emilio; Golahmar, Alireza; Niordson, Christian (2018). "A phase field formulation for hydrogen assisted cracking". Computer Methods in Applied Mechanics and Engineering. 342: 742–761. arXiv:1808.03264. Bibcode:2018CMAME.342..742M. doi:10.1016/j.cma.2018.07.021. S2CID 52360579.
^ Biben, Thierry; Kassner, Klaus; Misbah, Chaouqi (2005). "Phase-field approach to three-dimensional vesicle dynamics". Physical Review E. 72 (4): 041921. Bibcode:2005PhRvE..72d1921B. doi:10.1103/PhysRevE.72.041921. PMID 16383434.
^ Ashour, Mohammed; Valizadeh, Navid; Rabczuk, Timon (2021). "Isogeometric analysis for a phase-field constrained optimization problem of morphological evolution of vesicles in electrical fields". Computer Methods in Applied Mechanics and Engineering. Elsevier BV. 377: 113669. Bibcode:2021CMAME.377k3669A. doi:10.1016/j.cma.2021.113669. ISSN 0045-7825. S2CID 233580102.
^ Valizadeh, Navid; Rabczuk, Timon (2022). "Isogeometric analysis of hydrodynamics of vesicles using a monolithic phase-field approach". Computer Methods in Applied Mechanics and Engineering. Elsevier BV. 388: 114191. Bibcode:2022CMAME.388k4191V. doi:10.1016/j.cma.2021.114191. ISSN 0045-7825. S2CID 240657318.
^ Valizadeh, Navid; Rabczuk, Timon (2019). "Isogeometric analysis for phase-field models of geometric PDEs and high-order PDEs on stationary and evolving surfaces". Computer Methods in Applied Mechanics and Engineering. Elsevier BV. 351: 599–642. Bibcode:2019CMAME.351..599V. doi:10.1016/j.cma.2019.03.043. ISSN 0045-7825. S2CID 145903238.
^ G.J. Fix, 자유 경계 문제에서:이론과 응용, 에드A. Fasano and M. Primicerio, p. 580, Pitman (보스턴, 1983).
^ Langer, J. S. (1986). "Models of Pattern Formation in First-Order Phase Transitions". Directions in Condensed Matter Physics. pp. 165–186. Bibcode:1986SDCMP...1..165L. doi:10.1142/9789814415309_0005. ISBN 978-9971-978-42-6. {{cite book}}: journal=무시됨(도움말)
^ Langer, J. S. (1980). "Instabilities and pattern formation in crystal growth". Reviews of Modern Physics. 52 (1): 1–28. Bibcode:1980RvMP...52....1L. doi:10.1103/RevModPhys.52.1.
^ ^a ^b Karma, Alain; Rappel, Wouter-Jan (1998). "Quantitative phase-field modeling of dendritic growth in two and three dimensions". Physical Review E. 57 (4): 4323. Bibcode:1998PhRvE..57.4323K. doi:10.1103/PhysRevE.57.4323.
^ Hohenberg, P.; Halperin, B. (1977). "Theory of dynamic critical phenomena". Reviews of Modern Physics. 49 (3): 435. Bibcode:1977RvMP...49..435H. doi:10.1103/RevModPhys.49.435. S2CID 122636335.
^ Yue, Pengtao; Zhou, Chunfeng; Feng, James J. (2007). "Spontaneous shrinkage of drops and mass conservation in phase-field simulations". Journal of Computational Physics. 223 (1): 1–9. Bibcode:2007JCoPh.223....1Y. CiteSeerX 10.1.1.583.2109. doi:10.1016/j.jcp.2006.11.020.
^ Donaldson, A.A.; Kirpalani, D.M.; MacChi, A. (2011). "Diffuse interface tracking of immiscible fluids: Improving phase continuity through free energy density selection". International Journal of Multiphase Flow. 37 (7): 777. doi:10.1016/j.ijmultiphaseflow.2011.02.002.
^ McFadden, G.B.; Wheeler, A.A.; Anderson, D.M. (2000). "Thin interface asymptotics for an energy/entropy approach to phase-field models with unequal conductivities". Physica D: Nonlinear Phenomena. 144 (1–2): 154–168. Bibcode:2000PhyD..144..154M. doi:10.1016/S0167-2789(00)00064-6. hdl:2060/20000014455. S2CID 119641692.
^ Jacqmin, David (1999). "Calculation of Two-Phase Navier–Stokes Flows Using Phase-Field Modeling". Journal of Computational Physics. 155 (1): 96–127. Bibcode:1999JCoPh.155...96J. doi:10.1006/jcph.1999.6332.
^ Benítez, R.; Ramírez-Piscina, L. (2005). "Sharp-interface projection of a fluctuating phase-field model". Physical Review E. 71 (6): 061603. arXiv:cond-mat/0409707. Bibcode:2005PhRvE..71f1603B. doi:10.1103/PhysRevE.71.061603. PMID 16089744. S2CID 28956874.
^ Schmitz, G. J.; Böttger, B.; Eiken, J.; Apel, M.; Viardin, A.; Carré, A.; Laschet, G. (2011). "Phase-field based simulation of microstructure evolution in technical alloy grades". International Journal of Advances in Engineering Sciences and Applied Mathematics. 2 (4): 126. doi:10.1007/s12572-011-0026-y. S2CID 121915897.
^ Tanné, E.; Li, T.; Bourdin, B.; Marigo, J.-J.; Maurini, C. (2018). "Crack nucleation in variational phase-field models of brittle fracture" (PDF). Journal of the Mechanics and Physics of Solids. 110: 80–99. Bibcode:2018JMPSo.110...80T. doi:10.1016/j.jmps.2017.09.006. S2CID 20139734.
^ Kumar, A.; Bourdin, B.; Francfort, G. A.; Lopez-Pamies, O. (2020). "Revisiting nucleation in the phase-field approach to brittle fracture". Journal of the Mechanics and Physics of Solids. 142: 104027. Bibcode:2020JMPSo.14204027K. doi:10.1016/j.jmps.2020.104027.
^ Najem, Sara; Grant, Martin (2016-05-09). "Phase-field model for collective cell migration". Physical Review E. 93 (5): 052405. Bibcode:2016PhRvE..93e2405N. doi:10.1103/PhysRevE.93.052405. PMID 27300922.
^ "Phase-field model for cellular monolayers : a cancer cell migration studyauthors : Benoit Palmieri and Martin Grant Perimeter Institute". www2.perimeterinstitute.ca. Retrieved 2021-11-05.

추가열람

Chen, Long-Qing (2002). "Phase-Field models For microstructure evolution". Annual Review of Materials Research. 32: 113–140. doi:10.1146/annurev.matsci.32.112001.132041.
Moelans, Nele; Blanpain, Bart; Wollants, Patrick (2008). "An introduction to phase-field modeling of microstructure evolution". Calphad. 32 (2): 268. doi:10.1016/j.calphad.2007.11.003.
Steinbach, Ingo (2009). "Phase-field models in materials science". Modelling and Simulation in Materials Science and Engineering. 17 (7): 073001. Bibcode:2009MSMSE..17g3001S. doi:10.1088/0965-0393/17/7/073001. S2CID 3383625.
Fries, Suzana G.; Boettger, Bernd; Eiken, Janin; Steinbach, Ingo (2009). "Upgrading CALPHAD to microstructure simulation: The phase-field method". International Journal of Materials Research. 100 (2): 128. Bibcode:2009IJMR..100..128F. doi:10.3139/146.110013. S2CID 138203262.
Qin, R. S.; Bhadeshia, H. K. (2010). "Phase field method" (PDF). Materials Science and Technology. 26 (7): 803. Bibcode:2010MatST..26..803Q. doi:10.1179/174328409X453190. S2CID 136124682.
Donaldson, A.A.; Kirpalani, D.M.; MacChi, A. (2011). "Diffuse interface tracking of immiscible fluids: Improving phase continuity through free energy density selection". International Journal of Multiphase Flow. 37 (7): 777. doi:10.1016/j.ijmultiphaseflow.2011.02.002.
Gonzalez-Cinca, R.; Folch, R.; Benitez, R.; Ramirez-Piscina, L.; Casademunt, J.; Hernandez-Machado, A. (2003). "Phase-field models in interfacial pattern formation out of equilibrium". In Advances in Condensed Matter and Statistical Mechanics, ed. By E. Korutcheva and R. Cuerno, Nova Science Publishers (New York, ), Pp. 2004: 203–236. arXiv:cond-mat/0305058. Bibcode:2003cond.mat..5058G. 위상장 모형의 재검토
프로바타스, 니콜라스; 엘더, 켄 (2010)재료과학 및 공학에서의 위상장 방법바인하임, 독일:Wiley-VCH Verlag GmbH & Co. KgaA. Doi:10.1002/9783527631520ISBN 9783527631520
슈타인바흐(Steinbach): "양자-위상-장 물질의 개념:역동적 우주의 비상 중력", Zeitschrift für Naturforschung A 721 (2017) Doi:10.1515/zna-2016-0270
Schmitz, G.J: "중력에 대한 결합 엔트로피/위상장 접근법", 엔트로피 2017, 19(4) 151; Doi:10.3390/e19040151

[1] Boettinger, W. J.; Warren, J. A.; Beckermann, C.; Karma, A. (2002). "Phase-Field Simulation of Solidification". Annual Review of Materials Research. 32: 163–194. doi:10.1146/annurev.matsci.32.101901.155803.

[viscous-2] Folch, R.; Casademunt, J.; Hernández-Machado, A.; Ramírez-Piscina, L. (1999). "Phase-field model for Hele-Shaw flows with arbitrary viscosity contrast. II. Numerical study". Physical Review E. 60 (2): 1734–40. arXiv:cond-mat/9903173. Bibcode:1999PhRvE..60.1734F. doi:10.1103/PhysRevE.60.1734. PMID 11969955. S2CID 8488585.

[:0-3] Bourdin, B.; Francfort, G.A.; Marigo, J-J. (April 2000). "Numerical experiments in revisited brittle fracture". Journal of the Mechanics and Physics of Solids. 48 (4): 797–826. Bibcode:2000JMPSo..48..797B. doi:10.1016/S0022-5096(99)00028-9.

[:1-4] Bourdin, Blaise (2007). "Numerical implementation of the variational formulation for quasi-static brittle fracture". Interfaces and Free Boundaries: 411–430. doi:10.4171/IFB/171. ISSN 1463-9963.

[:2-5] Bourdin, Blaise; Francfort, Gilles A.; Marigo, Jean-Jacques (April 2008). "The Variational Approach to Fracture". Journal of Elasticity. 91 (1–3): 5–148. doi:10.1007/s10659-007-9107-3. ISSN 0374-3535. S2CID 120498253.

[6] Karma, Alain; Kessler, David; Levine, Herbert (2001). "Phase-Field Model of Mode III Dynamic Fracture". Physical Review Letters. 87 (4): 045501. arXiv:cond-mat/0105034. Bibcode:2001PhRvL..87d5501K. doi:10.1103/PhysRevLett.87.045501. PMID 11461627. S2CID 42931658.

[7] Martinez-Paneda, Emilio; Golahmar, Alireza; Niordson, Christian (2018). "A phase field formulation for hydrogen assisted cracking". Computer Methods in Applied Mechanics and Engineering. 342: 742–761. arXiv:1808.03264. Bibcode:2018CMAME.342..742M. doi:10.1016/j.cma.2018.07.021. S2CID 52360579.

[8] Biben, Thierry; Kassner, Klaus; Misbah, Chaouqi (2005). "Phase-field approach to three-dimensional vesicle dynamics". Physical Review E. 72 (4): 041921. Bibcode:2005PhRvE..72d1921B. doi:10.1103/PhysRevE.72.041921. PMID 16383434.

[Ashour_Valizadeh_Rabczuk_2021_p=113669-9] Ashour, Mohammed; Valizadeh, Navid; Rabczuk, Timon (2021). "Isogeometric analysis for a phase-field constrained optimization problem of morphological evolution of vesicles in electrical fields". Computer Methods in Applied Mechanics and Engineering. Elsevier BV. 377: 113669. Bibcode:2021CMAME.377k3669A. doi:10.1016/j.cma.2021.113669. ISSN 0045-7825. S2CID 233580102.

[Valizadeh_Rabczuk_2022_p=114191-10] Valizadeh, Navid; Rabczuk, Timon (2022). "Isogeometric analysis of hydrodynamics of vesicles using a monolithic phase-field approach". Computer Methods in Applied Mechanics and Engineering. Elsevier BV. 388: 114191. Bibcode:2022CMAME.388k4191V. doi:10.1016/j.cma.2021.114191. ISSN 0045-7825. S2CID 240657318.

[Valizadeh_Rabczuk_2019_pp._599–642-11] Valizadeh, Navid; Rabczuk, Timon (2019). "Isogeometric analysis for phase-field models of geometric PDEs and high-order PDEs on stationary and evolving surfaces". Computer Methods in Applied Mechanics and Engineering. Elsevier BV. 351: 599–642. Bibcode:2019CMAME.351..599V. doi:10.1016/j.cma.2019.03.043. ISSN 0045-7825. S2CID 145903238.

[12] G.J. Fix, 자유 경계 문제에서:이론과 응용, 에드A. Fasano and M. Primicerio, p. 580, Pitman (보스턴, 1983).

[13] Langer, J. S. (1986). "Models of Pattern Formation in First-Order Phase Transitions". Directions in Condensed Matter Physics. pp. 165–186. Bibcode:1986SDCMP...1..165L. doi:10.1142/9789814415309_0005. ISBN 978-9971-978-42-6. {{cite book}}: journal=무시됨(도움말)

[14] Langer, J. S. (1980). "Instabilities and pattern formation in crystal growth". Reviews of Modern Physics. 52 (1): 1–28. Bibcode:1980RvMP...52....1L. doi:10.1103/RevModPhys.52.1.

[thin-15] Karma, Alain; Rappel, Wouter-Jan (1998). "Quantitative phase-field modeling of dendritic growth in two and three dimensions". Physical Review E. 57 (4): 4323. Bibcode:1998PhRvE..57.4323K. doi:10.1103/PhysRevE.57.4323.

[16] Hohenberg, P.; Halperin, B. (1977). "Theory of dynamic critical phenomena". Reviews of Modern Physics. 49 (3): 435. Bibcode:1977RvMP...49..435H. doi:10.1103/RevModPhys.49.435. S2CID 122636335.

[17] Yue, Pengtao; Zhou, Chunfeng; Feng, James J. (2007). "Spontaneous shrinkage of drops and mass conservation in phase-field simulations". Journal of Computational Physics. 223 (1): 1–9. Bibcode:2007JCoPh.223....1Y. CiteSeerX 10.1.1.583.2109. doi:10.1016/j.jcp.2006.11.020.

[18] Donaldson, A.A.; Kirpalani, D.M.; MacChi, A. (2011). "Diffuse interface tracking of immiscible fluids: Improving phase continuity through free energy density selection". International Journal of Multiphase Flow. 37 (7): 777. doi:10.1016/j.ijmultiphaseflow.2011.02.002.

[19] McFadden, G.B.; Wheeler, A.A.; Anderson, D.M. (2000). "Thin interface asymptotics for an energy/entropy approach to phase-field models with unequal conductivities". Physica D: Nonlinear Phenomena. 144 (1–2): 154–168. Bibcode:2000PhyD..144..154M. doi:10.1016/S0167-2789(00)00064-6. hdl:2060/20000014455. S2CID 119641692.

[20] Jacqmin, David (1999). "Calculation of Two-Phase Navier–Stokes Flows Using Phase-Field Modeling". Journal of Computational Physics. 155 (1): 96–127. Bibcode:1999JCoPh.155...96J. doi:10.1006/jcph.1999.6332.

[21] Benítez, R.; Ramírez-Piscina, L. (2005). "Sharp-interface projection of a fluctuating phase-field model". Physical Review E. 71 (6): 061603. arXiv:cond-mat/0409707. Bibcode:2005PhRvE..71f1603B. doi:10.1103/PhysRevE.71.061603. PMID 16089744. S2CID 28956874.

[technical-22] Schmitz, G. J.; Böttger, B.; Eiken, J.; Apel, M.; Viardin, A.; Carré, A.; Laschet, G. (2011). "Phase-field based simulation of microstructure evolution in technical alloy grades". International Journal of Advances in Engineering Sciences and Applied Mathematics. 2 (4): 126. doi:10.1007/s12572-011-0026-y. S2CID 121915897.

[23] Tanné, E.; Li, T.; Bourdin, B.; Marigo, J.-J.; Maurini, C. (2018). "Crack nucleation in variational phase-field models of brittle fracture" (PDF). Journal of the Mechanics and Physics of Solids. 110: 80–99. Bibcode:2018JMPSo.110...80T. doi:10.1016/j.jmps.2017.09.006. S2CID 20139734.

[24] Kumar, A.; Bourdin, B.; Francfort, G. A.; Lopez-Pamies, O. (2020). "Revisiting nucleation in the phase-field approach to brittle fracture". Journal of the Mechanics and Physics of Solids. 142: 104027. Bibcode:2020JMPSo.14204027K. doi:10.1016/j.jmps.2020.104027.

[25] Najem, Sara; Grant, Martin (2016-05-09). "Phase-field model for collective cell migration". Physical Review E. 93 (5): 052405. Bibcode:2016PhRvE..93e2405N. doi:10.1103/PhysRevE.93.052405. PMID 27300922.

[26] "Phase-field model for cellular monolayers : a cancer cell migration studyauthors : Benoit Palmieri and Martin Grant Perimeter Institute". www2.perimeterinstitute.ca. Retrieved 2021-11-05.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

Search