커넥팅 로드를 통해 회전 크랭크에 연결된 비오프셋 피스톤의 왕복 운동은 운동 방정식으로 나타낼 수 있습니다.이 기사는 이러한 운동 방정식을 각도(각도 영역)와 시간(시간 영역)의 함수로서 미적분을 사용하여 어떻게 도출할 수 있는지를 보여준다.
크랭크축 지오메트리
피스톤, 로드 및 크랭크로 구성된 시스템의 형상은 다음 다이어그램에 나와 있습니다.

피스톤 핀, 크랭크 핀 및 크랭크 중앙의 기하학적 레이아웃을 보여주는 다이어그램 정의들
위 다이어그램에 표시된 지오메트리에서 다음 변수가 정의됩니다.
- {\ l 로드
 길이(피스톤 핀과 크랭크 핀 사이의 거리)
길이(피스톤 핀과 크랭크 핀 사이의 거리)
- {\ r 크랭크
 반지름(크랭크 센터와 크랭크 핀 사이의 거리, 즉 하프 스트로크)
반지름(크랭크 센터와 크랭크 핀 사이의 거리, 즉 하프 스트로크)
- A 크랭크
 각도(TDC의 실린더 중심선에서)
각도(TDC의 실린더 중심선에서)
- {\ x 피스톤
 핀 위치(크랭크 중심에서 실린더 보어 중심선을 따라 위쪽 거리)
핀 위치(크랭크 중심에서 실린더 보어 중심선을 따라 위쪽 거리)
다음 변수도 정의되어 있습니다.
- v 피스톤
 핀 속도(크랭크 중심에서 실린더 보어 중심선을 따라 이동)
핀 속도(크랭크 중심에서 실린더 보어 중심선을 따라 이동)
- a 피스톤
 핀 가속(실린더 보어 중심선을 따라 크랭크 중심에서 분리됨)
핀 가속(실린더 보어 중심선을 따라 크랭크 중심에서 분리됨)
- \omega 크랭크
 각속도( 각도와 동일한 방향/감각
각속도( 각도와 동일한 방향/감각
각속도
크랭크축의 회전 주파수(Hz)는 다음과 같이 엔진 속도(분당 회전수)와 관련이 있습니다.

따라서 크랭크축의 각 속도(라디안/초)는 다음과 같습니다.

삼각 관계
그림과 같이 크랭크 핀, 크랭크 센터 및 피스톤 핀은 삼각형 NOP를 형성합니다.
코사인 법칙에 따르면 다음과 같다.

서 l{\ 및 r {\
및 r {\ 은 하고 x displaystyle x}는
은 하고 x displaystyle x}는 A {\ A의
A {\ A의 변경에 달라집니다.
변경에 달라집니다.
각도 위치에 대한 방정식(각도 영역)
각도 영역 방정식은 각도의 함수로 표현됩니다.
유도 각도 영역 방정식
피스톤 왕복 운동의 각도 영역 방정식은 다음과 같이 시스템의 기하 방정식에서 도출됩니다.
위치
크랭크 각도에 대한 위치(삼각형 관계에서 정사각형 완성, 피타고라스 항등식 활용 및 정렬):

속도
크랭크 각도에 대한 속도(체인 규칙을 사용하여 첫 번째 도함수를 취함):

액셀러레이션
크랭크 각도와 관련된 가속도(체인 규칙 및 몫 규칙을 사용하여 2차 도함수를 취함):

비단순 고조파 운동
위의 각도 영역 방정식은 피스톤(로드 및 크랭크에 연결된)의 움직임이 단순한 고조파 운동이 아니라 크랭크의 회전과 함께 회전하는 로드의 움직임에 의해 수정된다는 것을 보여줍니다.이는 단순한 조화 운동을 직접 만들어내는 스카치 요크와는 대조적이다.
그래프 예시
각도 영역 방정식의 예는 다음과 같습니다.
시간에 관한 방정식(시간 영역)
시간 영역 방정식은 시간의 함수로 표현됩니다.
각속도도함수
각도는 다음과 같이 각 속도(\에 의한 시간과 관련됩니다.
의한 시간과 관련됩니다.

가 일정할 경우:
일정할 경우:

또, 다음과 같이 합니다.

시간 영역 방정식 도출
피스톤 왕복운동의 시간영역 방정식은 다음과 같이 각도영역 방정식으로부터 도출된다.
위치
시간에 대한 위치는 다음과 같습니다.

속도
시간에 대한 속도(체인 규칙 사용):

액셀러레이션
시간에 대한 가속도(체인 규칙 및 곱 규칙, 각 속도 파생물 사용):

각속도에 대한 스케일링
From the foregoing, you can see that the time domain equations are simply scaled forms of the angle domain equations:  is unscaled,
is unscaled,  is scaled by ω, and
is scaled by ω, and  is scaled by ω².
is scaled by ω².
각도 영역 방정식을 시간 영역으로 변환하려면 먼저 A를 t로 바꾼 다음 각 속도에 대해 스케일링합니다. x{\{ x}에 ,을 x { x에
,을 x { x에 ²²를 .
²²를 .
속도 최대값 및 최소값
정의상, 속도 최대값과 최소값은 가속도 0(수평축의 교차)에서 발생합니다.
크랭크 각도가 직각이 아님
속도 최대값 및 최소값(아래 그래프의 가속 제로 교차 참조)은 로드 l l 및 하프 r(\ r에
하프 r(\ r에 따라 달라지며 크랭크 A A가
따라 달라지며 크랭크 A A가 직각일 때는 발생하지 않습니다.
직각일 때는 발생하지 않습니다.
크랭크 로드 각도가 직각이 아님
크랭크가 로드와 직각을 이룰 때 반드시 최대 속도 및 최소 속도가 발생하는 것은 아닙니다."크랭크 로드 각도가 직각인 경우에만 최대 속도 및 최소 속도가 발생한다"는 문구를 반증하는 예가 있습니다.
예
로드 길이 6" 및 크랭크 반지름 2"의 경우(아래 예 그래프에 표시된 바와 같이) 가속 제로 크로싱을 수치적으로 풀면 최대/미니마가 ±73.17615°의 크랭크 각도로 나타납니다.그런 다음 삼각형의 사인 법칙을 사용하여 로드-수직 각도가 18.60647°이고 크랭크-로드 각도가 88.21738°인 것을 알 수 있습니다.분명히 이 예에서는 크랭크와 로드 사이의 각도가 직각이 아닙니다.삼각형 88.21738° + 18.60647° + 73.17615°의 각도를 합하면 180.00000°가 됩니다."크랭크가 로드와 직각을 이룰 때 속도 최대값/미니마가 발생한다"는 문구를 반증할 수 있는 하나의 반대 예시로 충분합니다.
피스톤 운동 예제 그래프
각도 도메인 그래프
아래 그래프는 고정 로드 l(\ l 과 하프 r(\r)
과 하프 r(\r) 의 다양한 값(1.8인치, 2.0인치, 2.2인치)에 대한 각도 영역 방정식을 보여 줍니다.그래프에서 L은 로드 l(\ l이고
의 다양한 값(1.8인치, 2.0인치, 2.2인치)에 대한 각도 영역 방정식을 보여 줍니다.그래프에서 L은 로드 l(\ l이고 R은 하프 스트로크입니다. r
R은 하프 스트로크입니다. r
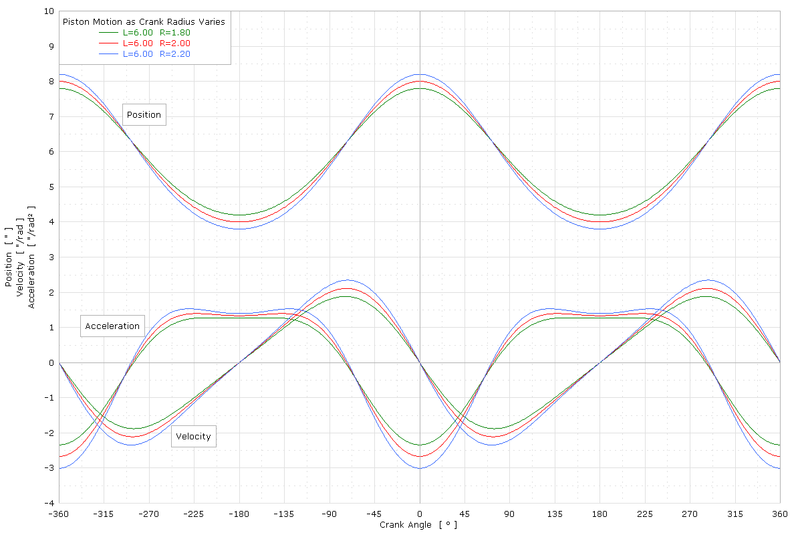
수직 축 단위는 위치의 경우 인치, 속도의 경우 [인치/라드], 가속도의 경우 [인치/라드²]입니다.수평축 단위는 크랭크 각도입니다. 애니매이션
아래는 위의 그래프와 동일한 로드 길이 및 크랭크 반지름 값을 갖는 피스톤 운동 방정식의 애니메이션입니다.
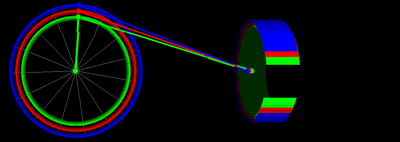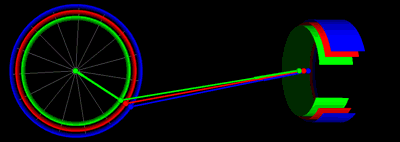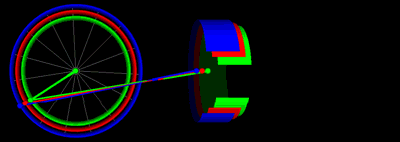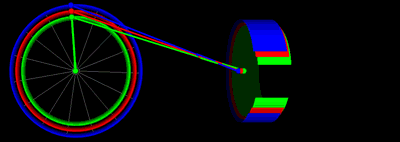
위 그래프에서 다양한 하프 스트로크를 사용한 피스톤 모션 애니메이션(동일한 색상 코드 사용)
편의 단위
자동차/핫로드 사용 사례의 경우 피스톤 로드 크랭크 형상에 가장 편리한 길이 단위는 인치이며, 일반적인 치수는 6인치(인치) 로드 길이와 2인치(인치) 크랭크 반지름입니다.이 문서에서는 위 그래프에 표시된 것처럼 위치, 속도 및 가속에 인치(") 단위를 사용합니다.
참고 항목
레퍼런스
외부 링크
- 애니메이션 엔진 애니메이션 오토 엔진
- 데스모스 인터랙티브 스트로크 대 로드 피스톤 위치 및 파생 모델
- desmos 인터랙티브 크랭크 애니메이션
- 코덱 피스톤 속도 및 가속도
- 유튜브 회전 SBC 350 엔진
- 유튜브 V8 엔진 3D 애니메이션
- 유튜브 내부 V8 엔진