위치 각도

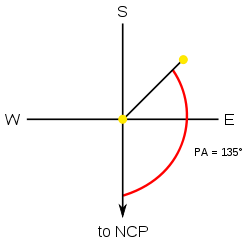
천문학에서 위치각(일반적으로 PA)은 하늘의 각도를 측정하는 규칙이다.국제천문연맹은 이것을 북극에 대해 측정된 각도로 정의하며, 적경의 방향으로 양의 각도로 변한다.표준(플립되지 않음) 이미지에서는 축을 기준으로 시계 반대 방향으로 양의 편각 방향으로 측정한 것입니다.

관측된 시각 쌍성의 경우, 이는 북극에 상대적인 주성으로부터의 보조성의 각도 오프셋으로 정의된다.

예에서 알 수 있듯이 PA가 135°인 가상의 쌍성을 관찰할 경우, 이는 북극에서 1차(P)로 그려진 접안 렌즈에 있는 가상의 선이 2차(S)에서 상쇄되어 각도가 135°가 된다는 것을 의미한다.

시각 바이너리를 그래프로 표시할 때 NCP는 일반적으로 주(Primary)인 중앙점(원점)에서 아래로 그려지며, PA는 시계 반대 방향으로 측정됩니다.또, 예를 들면, 그 위치각에 의해서 고유 운동의 방향을 알 수 있다.

위치 각도의 정의는 은하와 같은 확장된 물체에도 적용되며, 여기서 NCP 선으로 물체의 장축에 의해 만들어진 각도를 나타냅니다.

앵무새

위치각의 개념은 해양 항해에서 계승되며, 여기서 최적 나침반 코스는 알려진 위치에서 최소 노력으로 목표 위치 t까지의 코스이다.바람과 해류의 영향을 차치하고, 최적의 코스는 해수면의 두 위치 사이의 거리가 가장 작은 코스이다.나침반 코스를 계산하는 것은 측지학의 역문제로 알려져 있다.

이 기사에서는 일부 반지름을 가진 구면을 이동하는 s와 t 사이의 거리를 최소화하는 추상화만을 고려합니다. R: 배가 목표 위치에 도달하기 위해 어느 방향으로 방향을 잡아야 합니까?

지구 중심 좌표계

해면을 구면으로 근사하면 최적 방향에 대한 상세한 평가가 가능하다.표준 계산에서는 배가 측지위도 θ와_s 측지경도 θ에_s 위치하는데, 여기서 θ는 적도 북쪽의 경우 양의 것으로 간주되고, θ는 그리니치의 동쪽의 경우 양의 것으로 간주됩니다.구체의 중심에 있는 전역 좌표계에서 데카르트 성분은 다음과 같다.

$\displaystyle \mathbf {s}=R\left({\begin{array}{c}\cos \varphi _{s}\cos \cos \cos \varphi _{s}\sin \sin \varphi _{s}\endarray{s}\right})$

타깃 포지션은

$\displaystyle {\mathbf {t}=R\left({\begin{array}{c}\cos \varphi _{t}\cos \cos \varphi _{t}\sin \sin \varphi _{t}\endarray}}\right).}$

북극은 에 있다.

${\displaystyle {\mathbf {N}=R\left({\begin{array}{c}0\\0\1\end{array}}\right).}$

최소 거리 d는 s와 t를 통과하는 큰 원을 따른 거리입니다.구 중심과 대원을 포함하는 평면에서 계산됩니다.

${\displaystyle d_{s,t}=R\theta _{s,t}}$

여기서 θ는 구체의 중심에서 본 두 지점의 각 거리로 라디안 단위로 측정됩니다.각도의 코사인은 두 벡터의 점곱에 의해 계산됩니다.

$\displaystyle \mathbf {s} \cdot \mathbf {t} = R^{2} (\sin \varphi _{s}\sin \varphi _{t}+\cos \varphi _{t}\cos\{ta}) _sin \varphi _{t} \cos\cos\cos\{t} _t}$

만약 배가 북극으로 직항한다면, 이동 거리는 다음과 같다.

$\displaystyle d_{s,N}=R\theta _{s,N}=R(\pi /2-\varphi _{s})$

만약 배가 t에 출발하여 북극으로 곧장 헤엄쳐 간다면, 이동 거리는 다음과 같다.

$\displaystyle d_{t,N}=R\theta _{t,n}=R(\pi /2-\varphi _{t})}$

간단한 파생

구면^[1] 삼각법의 코사인 공식은 한 손에는 북쪽을 가리키고 다른 손에는 t를 가리키는 s를 통과하는 대원 사이의 각도 p를 산출한다.

$\cos \theta _{t,N}=\cos \theta _{s,t}\cos \theta _{s,N}+\sin \theta _{s,t}\sin \theta _{s,N}\cos 페이지}$

$\displaystyle \sin \varphi _{t}=\cos \theta _{s,t}\sin \theta _{s}+\sin \theta _{s,t}\cos \varphi _{s}\cos 페이지}$

사인식은 산출된다.

${\displaystyle {\frac _{t,N}}=frac {sin(\fracda _{t}-\fracda _{s}}{\sin \theta _{s,t}}}}$

이것을 sin θ에_s,t 대해 풀고 앞의 공식에 삽입하면 위치각의 탄젠트에 대한 식을 얻을 수 있다.

$\displaystyle \sin \varphi _{t}=\cos \theta _{s,t}\sin \varphi _{s}+{\frac {s}}{\sin p}}\cos \varphi _{t}\cos \varphi _{s}\cos \varphi _{s}$

${\displaystyle \tan p=sin(\displayda _{t}-\cos \varphi _{s}){\sin \varphi _{t}-\cos \theta _{s,t}\sin \varphi _{s}}.}$

긴 파생상품

짧은 도출은 부호(북쪽의 서쪽 또는 동쪽?)를 나타내지 않는 0과 θ 사이의 각도를 제공하기 때문에 역접선의 정확한 분기를 사용하여 전체 범위의 각도를 생성할 수 있도록 p의 사인 및 코사인 값을 별도로 산출하는 보다 명시적인 도출이 바람직하다.

계산은 s와 t 사이의 대원 구조에서 시작됩니다.이것은 구 중심, s 및 t를 포함하는 평면에 있으며 축을 중심으로 한 각도 θ에_s,t 의해 s를 회전시킨다.축은 대원 평면에 수직이며 두 위치의 정규화된 벡터 교차곱으로 계산됩니다.

${\displaystyle \mathbf {1}{R^{2}\sin \theta _{s,t}}\mathbf {s}\times \mathbf {t} =sn \sin \theta _{s,t}}}\lef {cosin} \vari} \times\f {s}s \cosda _{s}\cos \varphi _{s}\cos \varphi _{t}\sin(\cosda _{t}-\cosda _{s}\end{array}}\right).}$

구체의 중심에 중심이 있는 우측 경사 좌표계는 축 s, 축의 세 축에 의해 주어진다.

${\displaystyle \mathbf {s} _{\perp } =\mathbf {s} ={\sin \theta _{s,t}} \sin \tarray {c} \cos \varphi _{t}\cos \da {da{\varphi }phi _{t}\sin \varphi _{t}\sin \varphi _{t}\sin \varphi _{s}+\cos ^{2}\varphi _{s}\cos ^{2}\cos ^{s}-\cos \varphi _{s}\cos\cos \varda _{{s}\coss}varphi _{t}\cos(\cosda _{t}-\cosda _{s})]\end {array}\right)}$

그리고 축 ω.대원을 따라 있는 위치는

$\displaystyle \mathbf {s} (\theta )=\cos \theta \mathbf {s} +\sin \theta \mathbf {s} _{\perp},\display 0\leq \leq 2\pi.}$

나침반 방향은 두 벡터 s와_⊥ s를 삽입하고 θ=0에서 θ에 대한 벡터의 구배를 계산함으로써 주어진다.

${\displaystyle {\frac \theta } {\mid \theta = 0} = \mathbf {s} _{\perp } }$

각도 p는 s 지점에서 구에 접하는 평면의 두 직교 방향을 따라 이 방향을 분할하여 구를 구한다.두 방향은 단위 길이로 정규화된 θ 및 θ에 관한 s의 부분 도함수에 의해 주어진다.

$\displaystyle \mathbf {u} _{N}=\left({\begin{array}{c}-\sin \varphi _{s}\sin \varphi _{s}\cos \varaphi _{s}\endarray}\cos \varray\right)}$

${\displaystyle \mathbf {u} _{E}=\left({\begin{array}{c}-\sin \sin \sin \snambda _{s}\cos \s}\0\end{array}}}\right);}$

$\displaystyle \mathbf {u} _{N} \cdot \mathbf {s} = \mathbf {u} _{E} \cdot \mathbf {u} _{N}=0}$

u는_N 북쪽을 가리키고_E u는 동쪽을 가리킵니다.위치 각도 p는 s를 이 두 방향으로 투영합니다_⊥.

${\displaystyle {\mathbf{s}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \cos }$ ${\displaystyle }$ ${\displaystyle p{\mathbf{}}_{}}$ N + ${\displaystyle \sin p}$ ${\displaystyle p{\mathbf{}}_{}}$ p p$$ E \ $displaystyle$\$mathbf { s$ }$=$ \ $cos$ p , \ $mathbf { u$ }$_$ { $N$} + \ $sin$ p , \ $mathbf { u$ ,

여기서 양의 부호는 양의 위치 각도가 북쪽에서 동쪽으로 정의됨을 의미합니다.코사인 및 사인 p 값은 이 방정식에 두 단위 벡터를 곱하여 계산됩니다.

$\displaystyle \cos p=\mathbf {s}_{\perp }\cdot \mathbf {u}_{N}=mathbf {1}{\sin \theta _{s,t}}[\cos \varphi _{t}\sin \varphi _{s}\cos}_cos{\cos}}$

$\displaystyle \sin p=\mathbf {s}_{\perp}\cdot \mathbf {u}_{E}=mathbf {1}{\sin \theta _{s,t}}}[\cos \varphi _{t}\sin(\cosda _{t}-\cda _{t}-\mathda _{s})]}$

s의 복잡한_⊥ 식을 삽입하는 대신, 평가는 인수의 순환 이동 하에서 삼중곱이 불변함을 사용할 수 있다.

$(\displaystyle \cos p=(\mathbf {1}{R}\times\frac {1}{s}\mathbf {s}\times\mathbf {n})\cdot \mathbf {u}_{N})}$

atan2를 사용하여 값을 계산하면 두 식을 모두 cos θ로_t 나눗셈하고 sin θ로_s,t 곱하여 줄일 수 있습니다. 이러한 값은 항상 양의 값이고 연산은 부호를 바꾸지 않기 때문입니다.

${\displaystyle \tan p=syn(\displayda _{t}-\displayda _{s}){\cos \varphi _{t}-\sin \varphi _{s}\cos(\displayda _{t}-\da _{s})}}}}.}$

「 」를 참조해 주세요.

• 시차각
• 각거리

추가 정보

• Birney, D. Scott; Gonzalez, Guillermo; Oesper, David (2007). Observational Astronomy. Cambridge University Press. p. 75. ISBN 978-0-521-85370-5.

레퍼런스

외부 링크

• 시각 쌍성 150개의 궤도, Dibon Smith(2006년 2월 26일 접근)