이익 극대화
Profit maximization경제학에서 이익 극대화는 기업이 가장 높은 이윤으로 이어지는 가격, 입력 및 생산 수준을 결정할 수 있는 단기 또는 장기적 과정이다. 현재 미시경제학에 대한 주류 접근방식인 신고전주의 경제학은 보통 그 회사를 이윤 극대화 모델로 삼는다.
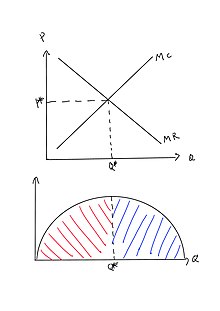
수익 극대화 예제 다이어그램:
수급 그래프에서 Q*의 출력은 MR과 MC의 교차점이다. 회사는 이 생산 수준에서 이윤을 극대화할 수 있다. (MR=MC) 적색 부분이 보여주듯이 평형수량의 산출량(Q*)보다 적게 생산되었을 때, MR은 MC보다 크다. 그 회사는 얻는 수익이 지불하는 비용보다 더 많기 때문에 추가 생산물을 생산한다. 그래서 총이익이 늘어날 것이다. 그러나 출력 레벨이 Q*보다 크면 파란색 부분과 같이 MR<MC. 추가적인 단위 수준이 수익보다 더 큰 비용을 증가시키기 때문에 확정 이익은 감소할 것이다. 따라서 총이익은 감소할 것이다.
이익 극대화에 대해 취할 수 있는 몇 가지 관점이 있다. 첫째, 이익은 수익에서 비용을 뺀 것이므로, 수익과 원가를 각각 그래픽으로 출력 수준의 함수로 표시하고 차이를 최대화하는 출력 수준을 찾을 수 있다(또는 그래프 대신 값표를 사용하여 수행할 수 있다). 둘째, 생산량 측면에서 구체적인 기능적 형태가 수익과 원가로 알려져 있다면, 미적분학을 이용하여 산출 수준에 관한 이익을 극대화할 수 있다. 셋째, 최적화를 위한 첫 번째 순서 조건은 한계 수익과 한계 비용을 동일시하기 때문에 한계 수익(mr)과 한계 비용(mc) 함수를 직접 사용할 수 있다면 방정식이나 그래프를 사용하여 이를 동일시할 수 있다. 넷째, 기업은 각 잠재적 출력수준의 생산원가를 제공하는 기능보다는 각 투입변수의 어떤 양이라도 획득하는 원가를 제공하는 투입원가 함수를 가질 수 있으며, 그 결과 어떤 투입량 조합을 사용함으로써 얼마나 많은 산출물이 발생하는지를 보여주는 생산함수를 가질 수 있다. 이 경우 투입원가 함수와 생산함수에 따라 투입사용수준에 관한 이익을 극대화하기 위해 미적분을 사용할 수 있다. 각 입력에 대한 첫 번째 주문 조건은 입력물의 한계 수익 산출물(사용된 입력물 양에 대한 증분으로 인한 제품 판매로 인한 수익 증가)과 입력물의 한계비용과 동일하다.
완벽하게 경쟁적인 생산량 시장에서 기업의 경우, 수익 기능은 단순히 시장가격에 생산되고 판매된 수량의 곱을 곱한 것과 같을 뿐 아니라 독점자의 경우 그것의 판매가격과 동시에 생산량의 수준을 선택할 것이다. 독점의 경우 여전히 정상적인 수익을 낼 수 있기 때문에 더 많은 제품을 생산할 것이다. 가장 많은 이익을 얻으려면 경쟁력 있는 시장보다 더 높은 가격과 낮은 수량을 책정해야 한다. 그러나, 수익 함수는 높은 수준의 산출물이 팔리기 위해서는 더 낮은 가격을 필요로 한다는 사실을 고려한다. 입력 시장에 대해 유사한 특징이 있다. 완벽한 경쟁적 입력 시장에서 기업의 입력 비용은 단순히 생산 시간에서 사용하기 위해 구매한 금액인 반면에, 단조로운 사람의 단위당 입력 가격은 구매한 입력물 양보다 높다.
단기매매와 장기매매차익 극대화의 주된 차이는 장기적으로는 실물자본을 포함한 모든 투입변수의 수량이 선택변수인 반면 단기적으로는 과거 투자결정에 의해 자본금액이 미리 결정된다는 점이다. 어느 경우든 노동력과 원자재의 투입이 있다.
이익 극대화의 한계 이익 극대화의 개념의 한계는 낮으며, 어떤 행동이라도 일정한 수준의 이익만을 가져오지는 않을 것이다. 반대로 여러 가지 수익수준을 낼 수 있고, 각각의 수익수준이 발생할 수 있다.
기본 정의
기업이 부담하는 원가는 고정원가와 변동원가의 두 그룹으로 분류할 수 있다. 단기적으로만 발생하는 고정비용은 제로 출력을 포함해 어느 수준의 생산물에서나 기업이 부담한다. 여기에는 장비 유지보수, 임대료, 단기적으로 그 수를 늘리거나 줄일 수 없는 직원의 임금, 일반적인 유지보수가 포함될 수 있다. 변동 비용은 생산 수준에 따라 변화하며, 더 많은 제품이 생성될수록 증가한다. 생산 중 소비되는 재료는 종종 이 범주에 가장 큰 영향을 미치는데, 여기에는 고려 중인 단기간의 고용 및 해고 가능 직원의 임금도 포함된다. 고정 비용 및 가변 비용, 조합된 총 비용.
수익은 보통 기업이 정상적인 사업 활동에서 받는 돈의 금액으로, (주식이나 채무발행과 같은 유가증권 판매에서 나오는 돈이 아니라) 재화와 용역의 판매에서 나온다.
5가지 방법은 리드, 대화율, 평균 달러 판매, 평균 판매 수, 평균 제품 이윤을 증가시키는 것이다. 이익은 최대 1000퍼센트까지 증가할 수 있다. 이는 대기업은 말할 것도 없고 유일한 무역업자와 중소기업에게 중요하다. 그러나 마찬가지로 모든 이익 극대화는 각 사업 단계와 이익 분배에 대한 더 큰 이익의 문제여서 임금과 동기부여가 더 높아진다.[1]
한계비용과 한계수익은 미적분 접근법의 취지에 따라 각 추가단위가 생산될 때 원가나 수익의 변화 또는 산출량에 관한 원가나 수익의 파생상품으로 정의된다. 예를 들어 첫 번째 정의를 들어, 기업이 5대를 생산하는 데 400달러, 6대를 생산하는 데 480달러가 든다면, 6호기의 한계비용은 80달러다. 반대로 6단위의 생산으로 인한 한계소득은 6단위의 생산에서 5단위의 생산에서 얻는 소득(후자 항목에서 앞 항목까지 뺀 것)을 뺀 소득이다.
총수익-총원가 관점
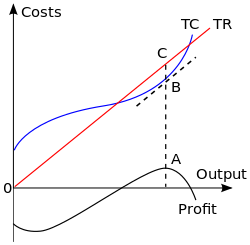
생산량을 극대화하는 이윤을 얻기 위해서는 총수익(TR)에서 총비용(TC)을 뺀 이익과 동일하다는 인식에서 출발한다. 각 수량에서 비용과 수익의 표를 주어진다면 방정식을 계산하거나 그래프에 직접 데이터를 표시할 수 있다. 이윤을 최대화하는 산출물은 이 차이가 최대치에 도달하는 산출물이다.
동봉된 도표에서 선형 총수익 곡선은 기업이 상품 시장에서 완벽한 경쟁자여서 자체 판매가격을 설정할 수 없는 경우를 나타낸다. 이익 극대화 출력 수준은 총수익이 C의 높이, 총원가가 B의 높이인 수준으로 표시되며, 최대 이익은 부문 CB의 길이로 측정된다. 이 생산수준은 또한 총 이익곡선이 최대치에 있는 수준이다.
그래프에서 가정된 것과 달리, 회사가 출력 시장에서 완벽한 경쟁자가 아니라면, 제품을 판매하는 가격은 회사의 최적 생산량에서 수요곡선을 읽어낼 수 있다. 이러한 최적 산출량은 한계수익이 한계원가와 동일한 수량이다.
한계수익-마진비용 관점
동등한 관점은 판매된 각 단위에 대해 한계이익(M³)이 한계수익(MR)에서 한계비용(MC)을 뺀 관계에 의존한다. 그 다음, 어느 정도의 산출물 수준에서 한계수익이 한계원가보다 크면 한계이익이 양성이므로 더 많은 양을 생산해야 하며 한계수익이 한계원가보다 작으면 한계이익이 음이 되고 더 적은 양을 생산해야 한다. 한계수익이 한계원가와 동일한 산출수준에서 한계이익은 0이며 이 수량은 이익을 최대화하는 것이다.[2] 한계이익이 양수일 때 총이익이 증가하고 한계이익이 음수일 때 총이익이 감소하기 때문에 한계이익이 영(0), 한계원가가 한계수익과 같으며, 낮은 생산수준이나 높은 생산수준이 더 낮은 수익수준에 도달해야 한다.[2] 미적분학 용어에서 최적 출력이 인접 출력 수준보다 더 높은 이익을 가져야 한다는 요구사항은 다음과 같다.[2]
MR과 MC의 교차점은 다음 도표에서 점 A로 표시된다. 만약 산업이 완벽하게 경쟁적이라면(도표에서 가정된 바와 같이), 기업은 한계수익곡선(MR)과 동일한 수요곡선(D)에 직면하게 되며, 이는 산업 수급에 의해 결정되는 가격에서의 수평선이다. 평균 총비용은 곡선 ATC로 나타낸다. 총 경제적 이익은 직사각형 PABC 영역으로 나타낸다. 최적 수량(Q)은 첫 번째 다이어그램의 최적 수량(Q)과 동일하다.
회사가 독점자인 경우, 한계 수익 곡선은 아래쪽으로 기울어진 시장 수요 곡선에 기초하기 때문에 다음 그래프와 같이 마이너스 기울기를 가질 것이다. 그래프에m Q로 표시된 최적 출력은 한계 원가가 한계 수익과 동일한 출력 수준이다. 그 산출량을 유도하는 가격은 그 수량(표시가m P)에서 수요곡선의 높이다.
경쟁적이지만 완벽하지는 않은 환경에서, 더 복잡한 이윤 극대화 솔루션은 게임 이론의 사용을 포함한다.
수익 극대화가 동등한 경우
어떤 경우에는 기업의 수요와 비용 조건이 모든 생산 수준의 최대 일정 한도 내에서 한계 이익이 0보다 클 수 있다.[3] 이 경우 한계이익은 최대치에 도달한 직후 0으로 곤두박질친다. 따라서 M³ = 0 규칙은 최대 수준에서 산출되어야 한다는 것을 의미하며, 이는 또한 수익을 최대화하는 수준이 된다.[3] 즉, 양과 가격을 극대화하는 이익은 한계수익을 0으로 설정하여 결정할 수 있으며, 한계수익을 최대 생산수준에서 발생하게 된다. 한계 수익은 총 수익 곡선이 최대값에 도달했을 때 0과 같다. 그 예로는 예정된 항공편을 들 수 있다. 한 명의 승객을 더 비행하는 데 드는 한계비용은 모든 좌석을 채울 때까지 무시할 수 있다. 그 항공사는 모든 좌석을 채움으로써 이익을 극대화할 것이다.
실생활의 이익 극대화
현실에서는 이익 극대화를 이루기가 쉽지 않다. 회사는 MR로 인해 마지막으로 판매된 상품의 한계수입과 한계비용을 정확하게 알아야 한다. 상품 수요의 가격탄력성은 다른 회사의 대응에 달려 있다. 유일하게 가격을 인상할 때 수요는 탄력적일 것이다. 한 가족이 가격을 올리고 다른 가족이 따라올 경우 수요는 비탄력적일 수 있다. 그러나 기업은 추정을 통해 이익 극대화를 도모할 수 있다. 가격 인상이 수요의 소폭 감소로 이어질 때 수요가 탄력받기 전에 가격을 최대한 올릴 수 있다. 일반적으로 가격 외에 다른 요인이 많아 수요가 발생할 수 있기 때문에 수요에 따라 가격의 영향을 바꾸기는 어렵다. 다양하다. 그 회사는 다른 목표와 고려사항도 가지고 있을 수 있다. 예를 들어, 기업들은 더 높은 시장 점유율을 추구하기 위해 최대 이익보다 적은 이익을 얻는 것을 선택할 수 있다. 가격 인상은 단기적으로 이익을 극대화하기 때문에 시장에 진출할 기업을 더 많이 유치할 것이다. 판매된 모든 제품/서비스의 비즈니스 비용을 습관적으로 기록하고 분석하십시오. 각 성공적인 판매의 모든 비용을 알 수 있을 때, 정확한 비용은 수익 분석에 도움이 된다. 그러나 비용에는 인건비, 자재비, 운송비, 광고비, 보관비 등 잡다한 물건들이 많다. 이러한 잡화 아이템은 종종 기업의 작은 비용이 되고 판매되는 상품이나 서비스와 관련이 있다.
모든 재무정보를 통합하여 지출비용 보고서를 기록하기 위해 비즈니스 인텔리전스 툴이 필요할 수 있으며, 이를 통해 기업은 운영과 관련된 모든 비용과 그 정확성을 명확하게 이해할 수 있다. 월별 또는 분기별로 변경사항과 그 이유를 확인하고, 가능한 경우 문제점 및 취약점을 기록하여 개선한다. 이러한 정보는 비즈니스 최적화를 개선하여 수익을 증대시키는 데 도움이 될 수 있다. 매출을 최적화하기 위한 수요를 예측하기 위해 많은 대기업들은 값싼 노동력으로 생산지를 외국으로 이전함으로써 비용을 최소화할 것이다(예: 나이키). 그러나 생산라인을 외국으로 옮기면 불필요한 운송비가 발생할 수 있다. 반면 제품 생산과 판매를 위한 시장 입지는 좁으면 수요 최적화를 개선할 수 있지만, 생산 비용이 훨씬 높을 때는 좋은 선택이 아니다. 특정 제품 시리즈의 생산을 늘리거나 줄이기 위해 운영 관리 예측을 수행하고 판매 데이터를 사용하여 수요 증가, 정체 또는 감소를 예측한다. 표준화된 수요 최적화 기능을 사용하여 수요 계획 프로세스를 강화하여 조직의 이익 극대화를 위한 필요성의 방향을 결정한다. 기획 및 실제 실행, 판매 및 운영 계획 과정에서 도움이 되는 "what if" 솔루션을 구현할 때는 공급망, 재고 관리, 판매 프로세스 등 회사의 운영에 대해 숙지할 필요가 있다. 기업 계획이 실현 불가능해지는 것을 방지하기 위해 제약 조건을 사용한다. 위의 정보를 사용하여 금융 및 공급망 관리 계획에 대한 가능한 해결책을 더 잘 예측하십시오.
총 비용 및 이익 극대화 변화
기업은 한계수익이 한계원가와 동일한 곳에서 영업함으로써 이익을 극대화한다. 단기적으로 고정비의 변화는 생산량이나 가격을 극대화하는 이익에는 영향을 미치지 않는다.[4] 그 회사는 단지 단기 고정 비용을 매몰 비용으로만 처리하고 이전과 같이 계속 운영한다.[5] 이것은 그래픽으로 확인할 수 있다. 총비용-총수익의 관점을 나타낸 도표를 사용하여, 기업은 총비용선과 총수익선의 경사가 같은 지점에서 이익을 극대화한다.[3] 고정비용이 증가하면 총원가곡선이 변경금액에 따라 경직적으로 상승하게 된다.[3] 총수익곡선이나 총원가곡선의 형태에는 영향이 없을 것이다. 따라서 산출량을 최대화하는 이익은 그대로 유지될 것이다. 이 점은 또한 한계 수익-마진 비용 관점에 대한 도표를 사용하여 설명할 수 있다. 고정 비용의 변화는 이러한 곡선의 위치나 형태에 영향을 미치지 않을 것이다.[3] 단순하게 보면 이익은 총비용 = TR-TC와 관련이 있지만 최대 이익(TR-TC의 최대 가치)까지 생산해 이익을 극대화할 수 있다. 그러나 총비용의 증가가 반드시 한계비용을 변화시키는 것은 아니기 때문에 총비용의 증가가 이익의 극대화를 의미하는 것은 아니다. 한계원가가 그대로 유지된다면 기업은 여전히 (MR=MC=Price) 단위로 생산하여 이윤을 극대화할 수 있다.
마크업 가격
기업의 최적의 생산 수준을 결정하는 방법을 사용하는 것 외에도, 완벽하게 경쟁적이지 않은 기업은 이윤을 극대화하기 위해 가격을 동등하게 설정할 수 있다(주어진 수요 곡선을 따라 가격을 설정하는 것은 생산하고 판매하기 위해 선호하는 수량을 선택하는 것과 같기 때문이다). 이익 극대화 조건은 위의 관점이 사용하는 것보다 "더 쉽게 적용할 수 있는" 형태나 경험칙으로 표현할 수 있다.[6] 첫 번째 단계는 한계 수익에 대한 표현을 다음과 같이 다시 쓰는 것이다.
여기서 P와 Q는 각각 가격과 수량의 이전 값과 새로운 값 사이의 중간점을 가리킨다.[6] 증분 생산단위의 한계수익은 두 부분으로 나뉜다. 첫째, 기업이 추가 생산단위를 판매함으로써 얻는 수익 또는 P∆Q라는 용어를 제공하는 수익이다. 추가 단위를 한계 단위라고 한다.[7] 1대를 추가 생산하여 P 가격에 판매하면 P의 수익이 발생한다. 또한, "기업이 더 높은 가격에 판매할 수 있는 유닛에서 손실되는 수익"[7] 즉, 더 많은 유닛을 판매하려는 노력 때문에 모든 유닛의 가격이 인하되지 않았다면 이를 고려해야 한다. 수익 손실이 발생한 이 단위를 영내외 단위라고 한다.[7] 즉, 추가 단위를 판매하면 가격이 소폭 하락하여 판매되는 모든 단위의 수익이 Q(∆P/∆Q)만큼 감소한다. 따라서 MR = P + Q(∆P/∆Q) = P +P(Q/P) = P + P/(PED), 여기서 PED는 기업의 고객의 수요곡선을 특징짓는 수요의 가격탄력성이며, 이는 부정적이다. 그런 다음 MC 설정 = MR은 MC = P + P/PED를 제공하므로 (P - MC)/P = -1/PED, P = MC/[1 + (1/PED)]를 부여한다. 따라서 최적의 마크업 규칙은 다음과 같다.
- (P - MC)/P = 1/(-PED)
- 또는 동등하게
즉, 한계원가에 대한 가격표시의 크기는 상품 수요의 가격탄력성의 절대값과 반비례한다는 규칙이다.[8]
최적의 마크업 규칙은 또한 비경쟁적 기업이 시장 수요곡선의 탄력적인 영역에서 생산한다는 것을 의미한다. 한계비용은 플러스 값이다. PED/(1+PED)라는 용어는 양수적이므로 PED가 -1과 -190 사이일 때만(즉, 수요가 해당 출력 수준에서 탄력적인 경우) P>0이다.[10] 이러한 결과의 이면에 있는 직관은 수요가 Q의1 가치에서 비탄력적인 경우 Q의 감소는 P를 비례적으로 증가시켜 수익 PQ를 증가시킬 것이다. Q의 감소는 또한 총비용의 감소로 이어질 것이기 때문에, 수익 증가와 비용 감소의 결합으로 인해 이익이 증가할 것이다. 따라서 Q는1 가능한 한 가장 높은 이익을 주지 않는다.
노동의 한계 생산물, 노동의 한계 수익 산출물, 이익 극대화
일반적인 규칙은 한계수익이 한계원가와 동일한 곳에서 그 양의 산출물을 생산함으로써 이익을 극대화한다는 것이다. 이익 극대화 문제도 입력측에서 접근할 수 있다. 즉, 변동 투입물의 활용을 극대화하는 이익은 무엇인가? [11] 이윤을 극대화하기 위해 기업은 "투입자의 한계수익 산출물이 한계비용과 동일한 시점까지" 투입변수의 사용을 증가시켜야 한다.[12] 따라서 수학적으로 이윤을 극대화하는 규칙은L MRPL = MC이며 여기서 첨자 L은 일반적으로 가정되는 변수 투입물인 노동력을 가리킨다. 한계수익 산출물은 변동 투입변수에서 단위변동당 총수익의 변화다. 즉, MRPL = trTR/lL이다. MRP는L 한계수입의 산물이며 노동의 한계생산물 또는 MRPL = MR x MP이다L.
차최적 이익 극대화
종종 기업들은 그들의 최적화 전략이 전형적으로 소비자들을 위해 생산되는 상품들의 차선적인 수량으로 이어지지만 그들의 이윤을 최대화하려고 시도할 것이다. 일정한 양을 생산하기로 결정할 때, 기업은 종종 전체 사회적 잉여를 감소시키는 희생을 감수하면서 자신의 생산자 잉여를 극대화하려고 할 것이다. 이 같은 사회잉여금 감소에 따라 자체 생산자잉여금 극대화를 선택하지 않은 것과 비교하면 소비자잉여금도 최소화된다.
정부규정
시장 쿼터는 시장에서 기업의 힘을 반영하고, 시장을 지배하는 기업은 매우 흔하며, 과도한 권력은 비홍 행위의 동기가 되는 경우가 많다. 약탈적 가격 결정, 동점, 가격 조작 및 기타 행위들은 시장에서 독점자의 과도한 힘의 위기를 반영하고 있다. 기업이 자신의 이익을 극대화하기 위해 권력을 남용하는 것을 막기 위한 시도로, 정부는 종종 그들의 트랙에서 그들을 막기 위해 개입한다. 이것의 주요한 예는 대부분의 산업 독점을 효과적으로 불법화하는 반독점 규제를 통해서이다. 이 규제를 통해 소비자들은 비록 회사 자체가 재정적으로 어려움을 겪을 수 있지만, 그들을 위해 봉사하는 회사와 더 나은 관계를 누리게 된다.
참고 항목
메모들
- ^ entrepreneur.com
- ^ Jump up to: a b c 립시(1975) 페이지 245-47.
- ^ Jump up to: a b c d e Samuelson, W and Marks, S(2003). 페이지 47.
- ^ Samuelson, W and Marks, S(2003). 페이지 52.
- ^ 랜드스버그, S(2002년).
- ^ Jump up to: a b 핀디크, R, 루빈펠트, D(2001) 페이지 333.
- ^ Jump up to: a b c Besanko, D.와 Beatigam, R. (2001) 페이지 408.
- ^ Jump up to: a b Samuelson, W and Marks, S(2003). 페이지 103-05.
- ^ 핀디크, R, 루빈펠트, D(2001) 페이지 341.
- ^ Besanko and Braeutigam(2005) 페이지 419.
- ^ Samuelson, W and Marks, S(2003). 230 페이지
- ^ Samuelson, W and Marks, S(2003). 23 페이지
참조
- Landsg, S (2002). Price Theory and Applications (fifth ed.). South-Western.
- Lipsey, Richard G. (1975). An introduction to positive economics (fourth ed.). Weidenfeld and Nicolson. pp. 214–7. ISBN 0-297-76899-9.
- Samuelson, W; Marks, S (2003). Managerial Economics (fourth ed.). Wiley.
외부 링크
- Fiona Maclachlan, Wolfram Demotion Project의 완벽한 경쟁에서의 이익 극대화.
- 이익 극대화: Techfunnel Project Richard Gulle의 포괄적인 가이드.
Tejvan Pettinger의 이익 극대화. Riverlogic의 [https://www.riverlogic.com/blog/three-steps-to-mastering-profit-maximization/ 규범적 이익 극대화를 위한 3단계]