적절한 형태론

대수 기하학에서 체계들 사이의 적절한 형태론은 복잡한 분석적 공간들 사이의 적절한 지도의 아날로그다.

어떤 저자들은 k 분야에 걸친 적절한 다양성을 완전한 다양성이라고 부른다.예를 들어, 필드 k에 대한 모든 투영적 다양성은 k에 대해 적절하다.복합수(예: 다양성)에 대한 유한형식의 체계 X는 고전적(유클리드) 위상이 있는 복합점 X(C)의 공간이 콤팩트하고 하우스도르프일 경우에만 C에 대해 적합하다.

폐쇄적인 몰입은 적절하다.형태론은 그것이 적절하고 준마인일 경우에만 유한하다.

정의

형태론 f: X → Y 체계는 형태론 Z → Y를 가진 모든 체계에 대해 섬유 생산물로부터의 투영인 경우 보편적으로 폐쇄되었다고 불린다.

X\time _{Y}Z\to Z

기초 위상학 공간의 폐쇄된 지도 입니다.계략의 형태론은 분리된 경우 유한한 유형으로, 보편적으로 폐쇄된 경우([EGA] II, 5.4.1 [1])라고 한다.하나는 또한 X가 Y보다 적절하다고 말한다.특히 필드 k에 대한 품종 X는 형태론 X → 스펙(k)이 적절하다면 k에 대해 적절하다고 한다.

예

자연수 n의 경우, 정류 링 R에 대한 투영 공간ⁿ P는 R에 대해 적절하다.투사형 형태는 적절하지만, 모든 적절한 형태들이 투사형인 것은 아니다.예를 들어, C에 대해 투영되지 않는 차원 3의 순탄하고 적절한 복합적인 다양성이 있다.^[1]필드 k에 양차원의 다양한 결합은 k보다 결코 적절하지 않다.좀 더 일반적으로, 계획의 적절한 어핀 형태론은 유한해야 한다.^[2]예를 들어, 형태론 A¹ → 스펙(k)은 보편적으로 닫히지 않기 때문에 필드 k에 대한 아핀 선 A가¹ k에 대해 적절하지 않다고 보는 것은 어렵지 않다.사실, 뒤로 밀리는 형태론

\mathb {A} ^{1}\time _{k}\mathb {A} ^{1}\mathb {A} ^1}에 \mathb {A} ^1}:{1

(x,y) ↦ y로 주어짐) 닫힌 부분집합 xy = 1 in A¹ × A¹ = A² = A가 A¹ - 0이므로 닫히지¹ 않는다.

적절한 형태론의 특성 및 특성

다음에서는 f: X → Y를 계획의 형태론이라고 한다.

두 가지 적절한 형태론의 구성이 적절하다.
적절한 형태론 f: X → Y의 어떤 기저 변화도 적절하다.즉, g: Z → Y가 어떤 형태의 체계라면, 그 결과의 형태론 X ×_Y Z → Z가 적당하다.
적절성은 (Zariski 토폴로지에서) 베이스의 국부적 특성이다.즉, Y가 일부 개방형 하위집합_i Y에 의해 적용되고 모든⁻¹ f(Y_i)에 대한 f의 제한이 적절하다면 F도 해당된다.
보다 강하게 fpqc 토폴로지의 베이스에서 적절성이 국소적이다.예를 들어, X가 필드 k에 대한 체계이고 E가 k의 필드 확장인 경우, X가 베이스 변경 X가_E E에 대해 적절한 경우에만 k에 대해 적합하다.^[3]
폐쇄적인 몰입은 적절하다.
더 일반적으로, 유한한 형태론은 적절하다.이것은 올라가는 정리의 결과물이다.
Deligne에 의해, 체계들의 형태론은 그것이 적절하고 준마인일 경우에만 유한하다.^[4]이는 형태론 f: X → Y가 노메테리아인 경우 다른 가정으로부터 따르는 유한 표시의 국소적이라면 그로텐디크에 의해 보여졌다.^[5]
체계 S에 대한 X 적합성과 S에 대해 Y가 분리된 경우, 형태론 X → S에 대한 Y의 이미지는 Y의 닫힌 부분집합이다.^[6]이는 콤팩트한 공간에서 하우스도르프 공간에 이르는 연속적인 지도의 영상이 닫힌 부분집합이라는 위상의 정리와도 유사하다.
스타인 요인화 정리에서는 국부적인 노메트리안 체계에 대한 어떤 적절한 형태론도 X → Z → Y로 인수될 수 있다고 기술하고 있는데, 여기서 X → Z는 적절하고, 추연적이며, 기하학적으로 연결된 섬유들을 가지고 있으며, Z → Y는 유한하다.^[7]
차우의 보조정리에서는 적절한 형태는 투영적인 형태와 밀접한 관련이 있다고 말한다.한 가지 버전은 다음과 같다: 만약 X가 준 컴팩트 체계 Y에 대해 적절하고 X가 미세하게 많은 (Y noeterian에 대해 자동인) 수정 불가능한 요소만 가지고 있다면, W가 Y에 대해 투영되는 투영적 처절함 형태론 g: W → X가 있다.더욱이 g는 X의 밀도 있는 오픈 서브셋 U에 비해 이형성이며, g⁻¹(U)는 W에 밀도 있다고 정리할 수 있다.X가 일체형이라면 W가 일체형이라고 정리할 수도 있다.^[8]
나가타의 콤팩트화 정리에서는, 델리인이 일반화시킨 바와 같이, 준 컴팩트 계수와 준 분리 계통 요인 사이에 유한 형태의 분리형 형태론이 오픈몰입에 이어 적절한 형태론이 뒤따른다고 말하고 있다.^[9]
국내noetherian 계획 사이의 적절한 morphisms이, 일관성 있는 단 F의 높은 직접적인 이미지 Rif∗(F)(특히 직접적인 이미지 f∗(F))일관성 있는(enhanced3세, 3.2.1)에.(4개인, 복잡한 분석적 공간 사이의 적절한 지도를 들, Grauert과 Remmert이 높은 직접적인 이미지 preserv을 보였다 일관성 있는 볏짚을 단을 보존하고 있다.ec일관성 있는 분석용 피복)매우 특별한 경우로서, 필드 k 위에 있는 적절한 체계 X에 대한 규칙적인 기능의 링은 k-벡터 공간으로서 유한한 치수를 가진다.이와는 대조적으로 k 위에 놓인 아핀 라인의 정규 함수 링은 다항 링 k[x]로, k-벡터 공간으로서 유한 치수를 가지지 않는다.
이것에 대해 약간 더 강한 진술도 있다: (EGA III, 3.2.4) harv error: no target: CITREFEGA_III(도움말) $f\colon X\to S$ : $f\colon X\to S$ → S $f\colon X\to S$ 을(를) 유한 유형의 형태론 $f\colon X\to S$ , S 로컬 노메테리아 $및$ F $F$ ${\mathcal {O}}_{X}$ ${\$ -module ${\mathcal {O}}_{X}$ .S에 대해 F의 지원이 적절한 경우, 각 i $i\geq 0$ 0 ${\displaystyle i\geq$ 0 $}$ 에 $i \ge 0$ 대해 높은 직접 $R^{i}f_{*}F$ $R^{i}f_{*}F$ $R^{i}f_{*}F$ $R^{i}f_{*}F$ $R^{i}f_{*}F$ $R^{i}f_{*}F$ 가 일관성이 $R^{i}f_{*}F$ 있다.
복잡한 숫자에 걸쳐 유한한 유형의 체계 X의 경우, 복잡한 점의 설정 X(C)는 고전적(유클리드) 위상을 사용하는 복합 분석 공간이다.X와 Y가 분리되어 있고 C보다 유한한 유형의 경우, 연속 지도 f: X(C) → Y(C)가 모든 콤팩트 세트의 역영상이 콤팩트하다는 점에서 적절한 경우에만 형태론 f: X(C) → Y(C)가 적절하다.^[10]
만약 f: X→Y와 g: Y→Z가 gf가 적절하고 g가 분리되어 있다면 f가 적절하다.예를 들어 다음과 같은 기준을 사용하여 쉽게 증명할 수 있다.

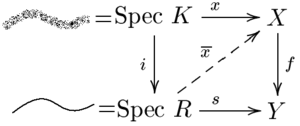
적정성 평가기준

체발리에게 돌아가는 적절성에 대한 매우 직관적인 기준이 있다.그것은 보통 적정성의 가치 기준이라고 불린다.Let f: X → Y는 유한 형태의 노메테리아식 계획의 형태론이다.Then f is proper if and only if for all discrete valuation rings R with fraction field K and for any K-valued point x ∈ X(K) that maps to a point f(x) that is defined over R, there is a unique lift of x to ${\overline {x}}\in X(R)$ . (EGA II, 7.3.8).More generally, a quasi-separated morphism f: X → Y of finite type (note: finite type includes quasi-compact) of *any* schemes X, Y is proper if and only if for all valuation rings R with fraction field K and for any K-valued point x ∈ X(K) that maps to a point f(x) that is defined over R, there is a unique lift of x to ${\d$ $isplaystyle {\overline{x}\in X(R)}$ . (Stacks project Tags 01KF 및 01KY).Spec K가 Spec R의 일반 지점이고 이산 평가 링은 정확히 정규 국부 1차원 링이라는 점에 유의하여, Y에 대한 정규 곡선(모형주의 s: Spec R → Y에 대응)과 X, F에 대한 이 곡선의 일반 포인트를 들어 올리는 것이 한 가지 방법이 정확하게 존재하는 경우에만 적절하다.커브를 완성하기 위해서.

마찬가지로, 모든 다이어그램에 최대 1개의 리프트 ${\overline {x}}\in X(R)$ X ${\overline {x}}\in X(R)$ ( $){\displaystyle {\x}\in$ X $(R)}$ 에 있는 경우에만 f가 분리된다 ${\overline {x}}\in X(R)$

예를 들어, 가치평가 기준을 고려할 때, 투영 공간ⁿ P가 필드(또는 Z 이상)에 걸쳐 적절한지 쉽게 확인할 수 있다.단순히 부분 필드 K가 있는 이산 평가 링 R의 경우, 모든 K 지점[x₀,...,x_n]의 투사 공간이 R 지점으로부터 온다는 것을 관측할 수 있다. 좌표를 스케일링하여 모든 것이 R에 있고 적어도 하나는 R에 있는 단위가 되도록 한다.

디스크를 사용한 기하학적 해석

One of the motivating examples for the valuative criterion of properness is the interpretation of ${\text{Spec}}(\mathbb {C} [[t]])$ as an infinitesimal disk, or complex-analytically, as the disk $\Delta =\{x\in \mathbb {C} : x <1\}$ .이는 모든 파워 시리즈가

$f(t)=\sum _{n=0}^{\nft }a_{n}t^{n}}}}$

원점을 중심으로 $r$ $반경$ r $r$ 의 일부 디스크에 수렴.그런 다음 좌표 변경을 사용하여 단위 디스크에 파워 시리즈로 표시할 수 있다.그런 $다음$ t ${\displaystyle t$ 을(를) 반전시키면, $\mathbb {C} [[t]][t^{-1}]=\mathbb {C} ((t))$ 은 링 C $\mathbb {C} [[t]][t^{-1}]=\mathbb {C} ((t))$ [ $\mathbb {C} [[t]][t^{-1}]=\mathbb {C} ((t))$ [ $\mathbb {C} [[t]][t^{-1}]=\mathbb {C} ((t))$ $\mathbb {C} [[t]][t^{-1}]=\mathbb {C} ((t))$ [ $\mathbb {C} [[t]][t^{-1}]=\mathbb {C} ((t))$ - $\mathbb {C} [[t]][t^{-1}]=\mathbb {C} ((t))$ $\mathbb {C} [[t]][t^{-1}]=\mathbb {C} ((t))$ = C $\mathbb {C} [[t]][t^{-1}]=\mathbb {C} ((t))$ ( $\mathbb {C} [[t]][t^{-1}]=\mathbb {C} ((t))$ ) ${\displaystyle \mathb {C} [[t$ ][t $][t^{-1}]=\mathb {C}($ t)}( $t)}$ 이 되며, 이는 $\mathbb {C} [[t]][t^{-1}]=\mathbb {C} ((t))$ 원점에 극이 있을 수 있는 동력계열이다.이는 $\Delta ^{*}=\{x\in \mathbb {C} :0<|x|<1\}$ 원점을 제거한 \mathb { $\Delta ^{*}=\{x\in \mathbb {C} :0<|x|<1\}$ } : 오픈 디스크 $\Delta ^{*}=\{x\in \mathbb {C} :0<|x|<1\}$ { x $\Delta ^{*}=\{x\in \mathbb {C} :0<|x|<1\}$ C $\Delta ^{*}=\{x\in \mathbb {C} :0<|x|<1\}$ : $\Delta ^{*}=\{x\in \mathbb {C} :0<|x|<1\}$ < x $\Delta ^{*}=\{x\in \mathbb {C} :0<|x|<1\}$ < $\Delta ^{*}=\{x\in \mathbb {C} :0<|x|<1\}$ $\Delta ^{*}=\{x\in \mathbb {C} :0<|x|<1\}$ ${\displaystyle \Delta ^{*}=\{x\in \mathb$ { $C} :0<$ x $<1\}}})$ 로 토폴로지적으로 표현된다. ${\text{Spec}}(\mathbb {C} )$ ) ${\text{Spec}(\mathb {C} )$ 을(를) 통한 체계 형태론의 경우 ${\text{Spec}}(\mathbb {C} )$ 이는 대응 다이어그램에 의해 제시된다.

$디스플레이 스타일 {\displaystyle}\델타 ^{*}&\to &X\\\downarrow \\downarrow \\\delta &\to &Y\end{matrix}}$

그런 다음, 적정성에 대한 가치 평가 $\Delta ^{*}$ 은 Δ $\Delta ^{*}$ Δ Δ $0\in \Delta }$ 의 이미지에서 $0\in \Delta$ 점 $0\in \Delta$ ${\$ 을 채우는 것이 될 것이다 $\Delta ^{*}$

예

적절성의 가치적 기준이 닫힌 컴팩트 다지관과 유사한 공간을 왜 유지해야 하는지를 보기 위해 반례를 보는 것이 유익하다.If we take $X=\mathbb {P} ^{1}-\{x\}$ and $Y={\text{Spec}}(\mathbb {C} )$ , then a morphism ${\text{Spec}}(\mathbb {C} ((t)))\to X$ factors through an affine chart of $X$ , reducing the diagr에게 있다

${\begin{matrix}{\text{Spec})(\mathb {C}((t)))&\to &{\text{Spec}(\mathb {C}[t,t^{-1}])))\\downarrow &&\downarrow \\\{\text{Spec}(\mathb {C}[t]))&\to &{\text}{Spec}(\mathb {C})\end{matrix}}$

여기서 ${\text{Spec}}(\mathbb {C} [t,t^{-1}])=\mathbb {A} ^{1}-\{0\}$ [ t ${\text{Spec}}(\mathbb {C} [t,t^{-1}])=\mathbb {A} ^{1}-\{0\}$ ${\text{Spec}}(\mathbb {C} [t,t^{-1}])=\mathbb {A} ^{1}-\{0\}$ - ${\text{Spec}}(\mathbb {C} [t,t^{-1}])=\mathbb {A} ^{1}-\{0\}$ = ${\text{Spec}}(\mathbb {C} [t,t^{-1}])=\mathbb {A} ^{1}-\{0\}$ - { ${\text{Spec}}(\mathbb {C} [t,t^{-1}])=\mathbb {A} ^{1}-\{0\}$ ${\displaystyle {\text{Spec}(\mathb {C}[t,t^{-1}])$ $=\mathble {A}$ ^{1 $}-\{0\}}$ 은(는 $\{x\}$ $X$ ${\displaystyle$ $\{x\}$ \{x $\}$ 을(를) 중심으로 한 차트로서 ${\text{Spec}}(\mathbb {C} [t,t^{-1}])=\mathbb {A} ^{1}-\{0\}$ , 이 차트는 유사 알제브라의 공통 도표를 제공한다 $X$

${\begin{matrix}\mathb {C}((t)&\leftarrow &\uparrow \\mathb {C}[t]&\좌측 화살표 &\mathb {C} \end{matrix}$

Then, a lifting of the diagram of schemes, ${\text{Spec}}(\mathbb {C} [[t]])\to {\text{Spec}}(\mathbb {C} [t,t^{-1}])$ , would imply there is a morphism $\mathbb {C} [t,t^{-1}]\to \mathbb {C} [[t]]$ sending $t\mapsto t$ $t\mapsto t$ bras t $t\mapsto t$ 은(는) 알헤브라의 정류 도표에서 $t\mapsto t$ 볼 수 있다 $t\mapsto t$ 물론 이런 일은 있을 수 없다.따라서 $X$ $X$ 은(는) $Y$ $Y$ 에 대해 적합하지 $X$ 않다 $Y$

곡선이 있는 기하학적 해석

이 정리가 왜 유지되어야 하는지에 대한 직관의 일부를 포착하는 적절성의 가치평가 기준의 또 다른 유사한 예가 있다. $곡선$ C{\ $displaystyle C}$ 과 $C$ $C-\{p\}$ C $C-\{p\}$ - $C-\{p\}$ { $C-\{p\}$ {\ $displaystyle C-\{p\}$ 의 보완을 고려하십시오 $C-\{p\}$ 그러면 적절성에 대한 가치 기준이 다이어그램으로 읽힐 것이다.

${\begin{p\}&\rightarrow &X\\\downarrow \\c&\rightarrow &Y\end{matrix}}$

$C\to X$ → $C\to X$ ${\displaystyle C\to$ X $}$ 의 리프팅과 함께 $C\to X$ 기하학적으로 이것은 구조 $X$ {\ $displaystyle$ X $}$ 의 모든 곡선이 콤팩트한 곡선으로 완성될 수 있다는 $X$ 것을 의미한다.이 직관은 위상학적 공간의 형태론에 대한 체계적 이론적 해석과 콤팩트한 섬유들 중 하나에 있는 순서가 수렴해야 하는 것과 일치한다.Because this geometric situation is a problem locally, the diagram is replaced by looking at the local ring ${\mathcal {O}}_{C,{\mathfrak {p}}}$ , which is a DVR, and its fraction field ${\text{Frac}}({\mathcal {O}}_{C,{\mathfrak {p}}})$ .그런 다음 리프팅 문제가 정류 도표를 제시한다.

${\begin{matrix}{\text{Spec}({\text{Frac})({\mathcal{O}_{\mathfrak {p}})&\rightarrow &X\\\downarrow &&\downarrow \\\text{Sp}}({\mathcal{O}_{C,{\mathfrak{p}}})&\rightarrow &Y\end{matrix}}}}$

where the scheme ${\text{Spec}}({\text{Frac}}({\mathcal {O}}_{C,{\mathfrak {p}}}))$ represents a local disk around ${\mathfrak {p}}$ with the closed point ${\mathfrak {p}}$ removed.

형식 계획의 적절한 형태론

$f\colon {\mathfrak {X}}\to {\mathfrak {S}}$ f $f\colon {\mathfrak {X}}\to {\mathfrak {S}}$ : $f\colon {\mathfrak {X}}\to {\mathfrak {S}}$ → $f\colon {\mathfrak {X}}\to {\mathfrak {S}}$ ${\$ 은(는) 국소적으로 noetherian 공식 체계 사이의 형태론이다 $f\colon {\mathfrak {X}}\to {\mathfrak {S}}$ .We say f is proper or ${\mathfrak {X}}$ is proper over ${\mathfrak {S}}$ if (i) f is an adic morphism (i.e., maps the ideal of definition to the ideal of definition) and (ii) the induced map $f_{0}\colon X_{0}\to S_{0}$ is proper, where $X_{0}=({\mathfrak {X}},{\mathcal {O}}_{\mathfrak {X}}/I),S_{0}=({\mathfrak {S}},{\mathcal {O}}_{\mathfrak {S}}/K),I=f^{*}(K){\mathcal {O}}_{\mathfrak {X}}$ ${\$ $S_{0}=({\mathfrak {S},{\mathcal {O}_{\mathfrak {S}/K),$ $I=f^{*}{*(K){\mathcal{O}$ _{\ $mathfrak{X}},$ K는 $X_{0}=({\mathfrak {X}},{\mathcal {O}}_{\mathfrak {X}}/I),S_{0}=({\mathfrak {S}},{\mathcal {O}}_{\mathfrak {S}}/K),I=f^{*}(K){\mathcal {O}}_{\mathfrak {X}}$ ${\mathfrak {S}}$ ${\$ ${\mathfrak {S}}$ (EGA III, 3.4.1) harv 오류: no target: CITREFEA_의 정의 이상이다.III (도움말) 이 정의는 K의 선택과 무관하다.

공식적인 s의 예를 들어 Z의 공식적인 성공에 g:Y국내noetherian한 계획들이 → Z은 적절한 사상, Z0는 닫힌 집합 및 Y의 g(Y0)⊂ Z0 다음 사상 g^:Y/Y0→ Z/Z0{\displaystyle{\widehat{g}}\colon Y_{/Y_{0}}\to Z_{/Z_{0}그런 Y0는 닫힌 부분 집합}}은 적절한 사상화학 무기.es

그로텐디크는 이 설정에서 일관성 정리를 증명했다.즉, $f\colon {\mathfrak {X}}\to {\mathfrak {S}}$ : $f\colon {\mathfrak {X}}\to {\mathfrak {S}}$ → $f\colon {\mathfrak {X}}\to {\mathfrak {S}}$ ${\$ 은(는) 현지 노메트리안 공식 체계의 적절한 형태론이다 $f\colon {\mathfrak {X}}\to {\mathfrak {S}}$ .F가 ${\mathfrak {X}}$ ${\$ 의 일관성 있는 피복인 경우, 높은 직접 이미지 $R^{i}f_{*}F$ f $R^{i}f_{*}F$ $R^{i}f_{*}F$ ${\displaystyle$ R $^{i}f_{*}F}$ 가 일치한다 $R^{i}f_{*}F$ .^[11]

참고 항목

참조

^ Hartshorne(1977), 부록 B, 사례 3.4.1.
^ 류(2002년), 레마 3.3.17.
^ Stacks Project, Tag 02YJ.
^ Grotendieck, EGA IV, Part 4, Corollaire 18.12.4; .
^ Grotendieck, EGA IV, Part 3 Théoreme 8.11.1.
^ Stacks Project, Tag 01W0.
^ Stacks Project, Tag 03GX.
^ Grotendieck, EGA II, Corollaire 5.6.2.
^ 콘래드(2007), 정리 4.1.
^ SGA 1, XII 제안 3.2. (도움말)
^ Grotendieck, EGA III, Part 1 Théoreme 3.4.2.

Conrad, Brian (2007), "Deligne's notes on Nagata compactifications" (PDF), Journal of the Ramanujan Mathematical Society, 22: 205–257, MR 2356346
Grothendieck, Alexandre; Dieudonné, Jean (1961). "Éléments de géométrie algébrique: II. Étude globale élémentaire de quelques classes de morphismes". Publications Mathématiques de l'IHÉS. 8: 5–222. doi:10.1007/bf02699291. MR 0217084., 섹션 5.3. (적절함의 정의), 섹션 7.3 (적절함의 결정기준)
Grothendieck, Alexandre; Dieudonné, Jean (1961). "Eléments de géométrie algébrique: III. Étude cohomologique des faisceaux cohérents, Première partie". Publications Mathématiques de l'IHÉS. 11: 5–167. doi:10.1007/bf02684274. MR 0217085.
Grothendieck, Alexandre; Dieudonné, Jean (1966). "Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Troisième partie". Publications Mathématiques de l'IHÉS. 28: 5–255. doi:10.1007/bf02684343. MR 0217086., 제15.7절 (노에테리아식 계획을 반드시 수립할 필요는 없는 것으로 평가 기준을 일반화)
Grothendieck, Alexandre; Dieudonné, Jean (1967). "Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Quatrième partie". Publications Mathématiques de l'IHÉS. 32: 5–361. doi:10.1007/bf02732123. MR 0238860.
Hartshorne, Robin (1977), Algebraic Geometry, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157
Liu, Qing (2002), Algebraic geometry and arithmetic curves, Oxford: Oxford University Press, ISBN 9780191547805, MR 1917232

외부 링크

V.I. Danilov (2001) [1994], "Proper morphism", Encyclopedia of Mathematics, EMS Press
The Stacks Project Authors, The Stacks Project

[1] Hartshorne(1977), 부록 B, 사례 3.4.1.

[2] 류(2002년), 레마 3.3.17.

[3] Stacks Project, Tag 02YJ.

[4] Grotendieck, EGA IV, Part 4, Corollaire 18.12.4; .

[5] Grotendieck, EGA IV, Part 3 Théoreme 8.11.1.

[6] Stacks Project, Tag 01W0.

[7] Stacks Project, Tag 03GX.

[8] Grotendieck, EGA II, Corollaire 5.6.2.

[9] 콘래드(2007), 정리 4.1.

[10] SGA 1, XII 제안 3.2. (도움말)

[11] Grotendieck, EGA III, Part 1 Théoreme 3.4.2.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

Search