펄스 쉐이핑
Pulse shaping전자통신과 통신에서 펄스 쉐이핑은 전송된 펄스의 파형을 바꾸는 과정이다. 그것의 목적은 일반적으로 전송의 유효 대역폭을 제한함으로써 전송 신호를 그것의 목적이나 통신 채널에 더 잘 적합하게 만드는 것이다. 전송된 펄스를 이런 식으로 여과함으로써 채널에 의해 야기되는 심볼간 간섭을 통제할 수 있다. RF 통신에서는 신호를 주파수 대역에 맞추려면 펄스 쉐이핑이 필수적이다.
일반적으로 펄스 쉐이핑은 라인 코딩과 변조 후에 발생한다.
펄스 쉐이핑 필요
대역제한 채널을 통해 높은 변조 속도로 신호를 전송하면 심볼간 간섭이 발생할 수 있다. 그 이유는 푸리에 서신 때문이다(푸리에 변환 참조). 대역 제한 신호는 인접한 펄스가 겹치는 무한 시간 신호에 해당한다. 변조 속도가 증가하면 신호의 대역폭도 증가한다.[1] 신호의 스펙트럼이 예리한 직사각형인 순간, 이는 시간영역의 sinc 형상으로 이어진다. 신호의 대역폭이 채널 대역폭보다 커서 왜곡으로 이어질 경우 이런 현상이 발생한다. 이러한 왜곡은 대개 ISI(Insymbol interference, ISI)로 나타난다. 동기 형태의 펄스에 대해서는 이론적으로, 인접한 펄스가 완벽하게 정렬되어 있으면, 즉, 서로 0으로 교차하는 경우 ISI가 없다. 그러나 이것은 매우 좋은 동기화와 떨림 없이 정밀/안정적인 샘플링을 필요로 한다. ISI를 결정하기 위한 실용적인 도구로서, 채널의 일반적인 효과와 동기화/주파수 안정성을 시각화하는 Eye 패턴을 사용한다.
신호의 스펙트럼은 송신기에서 사용하는 변조 방식과 데이터 속도에 의해 결정되지만 펄스 형상 필터로 수정할 수 있다. 이 펄스 형상은 스펙트럼을 매끄럽게 만들어 다시 시간 제한 신호로 이어질 것이다. 일반적으로 전송된 기호는 기호와 곱한 디락 델타 펄스의 시간 시퀀스로 표현된다. 이것은 디지털에서 아날로그 영역으로의 공식적인 전환이다. 이때 신호의 대역폭은 무제한이다. 그런 다음 이 이론적 신호는 전송된 신호를 생성하면서 펄스 형상 필터로 필터링된다. 펄스 쉐이핑 필터가 시간 영역의 직사각형인 경우(일반적으로 그릴 때 이 작업이 수행되는 것처럼), 이는 무제한 스펙트럼으로 이어질 수 있다.
많은 기본 대역 통신 시스템에서 펄스 형상 필터는 암시적으로 박스카 필터다. 그것의 푸리에 변환은 sin(x)/x 형식이며, 기호 속도보다 높은 주파수에서 상당한 신호 힘을 가진다. 광섬유나 심지어 트위스트 페어 케이블을 통신 채널로 사용할 경우 이는 큰 문제가 되지 않는다. 그러나 RF 통신에서는 대역폭이 낭비되고, 단일 전송에는 엄격히 지정된 주파수 대역만 사용된다. 즉, 신호의 채널은 대역제한이다. 따라서 특정 기호 속도에 필요한 대역폭을 최소화하기 위해 더 나은 필터가 개발되었다.
전자 장치의 다른 영역에서는 상승 시간이 짧아야 하는 펄스의 생성이 한 가지 예로서, 이를 위한 한 가지 방법은 느리게 상승하는 펄스에서 시작하여 상승 시간을 줄이는 것이다(예: 스텝 복구 다이오드 회로).
여기서 이러한 설명은 대부분의 효과를 다루는 실무 지식을 제공하지만, 분석 기능으로 이어질 수 있는 인과관계를 포함하지는 않는다. 이것을 완전히 이해하기 위해서는 힐버트 변환이 필요한데, 이 변환은 Hubiside 단계 함수를 가진 콘볼루션에 의한 인과관계를 포함한다. 이것은 베이스밴드 설명의 실제 부분과 가상 부분을 결합하여 구조를 추가한다. 이는 즉시 실제 부분이나 가상 부분 중 하나가 분석 신호를 설명하기에 충분하다는 것을 암시한다. 소음이 많은 환경에서 두 신호를 모두 측정하면 원래 신호를 더 잘 재구성하는 데 사용할 수 있는 이중화 기능이 있다. 물리적 실현은 분석 신호가 정보를 전달하기 때문에 항상 인과적이다.
펄스 쉐이핑

모든 필터를 펄스형 필터로 사용할 수 있는 것은 아니다. 필터 자체는 심볼 간 간섭을 도입해서는 안 된다. 특정 기준을 충족해야 한다. 나이키스트 ISI 기준은 송신기 신호의 주파수 스펙트럼과 심볼 간 간섭을 연관시키기 때문에 흔히 사용되는 평가 기준이다.
통신 시스템에서 일반적으로 발견되는 펄스 쉐이핑 필터의 예는 다음과 같다.
송신자 측 펄스 쉐이핑은 종종 시스템의 노이즈에 대한 최적의 허용오차를 달성하기 위해 수신자 측 일치 필터와 결합된다. 이 경우 펄스 쉐이핑은 송신기와 수신기 필터 사이에 균등하게 분배된다. 따라서 필터의 진폭 응답은 시스템 필터의 포인트별 제곱근이다.
복잡한 펄스 형성 필터를 제거하는 다른 접근법이 개발되었다. OFDM에서 통신사는 매우 느리게 변조되어 각 통신사는 사실상 채널의 대역폭 제한에 영향을 받지 않는다.
싱크 필터
주파수 영역 등가물이 직사각형 모양이어서 박스카 필터로도 불린다. 이론적으로 최고의 펄스 조절 필터는 sinc 필터일 것이지만 정확하게 구현될 수는 없다. 상대적으로 꼬리가 서서히 부패하는 비침습 필터다. 위상 오류가 발생하면 심볼 간 간섭이 급격히 증가하기 때문에 동기화의 관점에서도 문제가 있다.
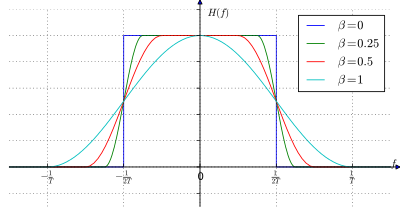
상승 코사인 필터
상승 코사인은 sinc와 유사하며, 약간 더 큰 스펙트럼 폭에 대해 더 작은 측면부의 절충이 있다. 상승 코사인 필터는 구현이 실용적이며 널리 사용되고 있다. 그들은 구성 가능한 초과 대역폭을 가지고 있기 때문에 통신 시스템은 더 단순한 필터와 스펙트럼 효율 사이에서 절충을 선택할 수 있다.
가우스 필터
이것은 가우스 함수처럼 생긴 출력 펄스를 제공한다.
참고 항목
참조
- ^ Lathi, B. P. (2009). Modern digital and analog communication systems (4th ed.). New York: Oxford University Press. ISBN 9780195331455.
- John G. Proakis, "디지털 커뮤니케이션, 제3판" 1995년 맥그로-힐 북 주식회사 9장 ISBN 0-07-113814-5
- IMT-2000 3GPP - 국가 계기 신호 발생기 튜토리얼, 스펙트럼 효율성 향상을 위한 펄스 형성
- National Instruments Measurement 기초 자습서, 통신 시스템의 펄스 형태 필터링
- Erkin Cubuku(ntrs.nasa.gov)의 통신 시스템 내 루트 상승 코사인 필터 및 펄스 형성


