통계함수
통계 에서 Q-함수 는 표준 정규 분포 의 꼬리 분포 함수 다.[1] [2] 즉 Q x {\displaystyle Q(x)} 랜덤 변수 가 x {\displaystyle x} 동등하게 Q x {\displaystyle Q(x)} x {\displaystyle x} .
Y {\displaystyle Y} μ {\displaystyle \ mu } 와 displaystyle ^{2 랜덤 , X μs {\ displaystystyle ={\Y-\ma }{\ }}}}}}}}}}}}} 표준 정상 이며시그마
P ( Y > y ) = P ( X > x ) = Q ( x ) {\displaystyle P(Y)=P(X)=Q(x)} 여기서 x y {\ displaystyle x={\frac {y-\mu }{\ma
Q-함수의 다른 정의들, 모두 정상 누적분포함수 의 단순한 변형인 Q-함수의 정의도 가끔 사용된다.[3]
정규 분포 의 누적분포함수와 관계가 있기 때문에 Q함수는 응용수학과 물리학의 중요한 함수인 오차함수 측면에서도 표현할 수 있다.
정의 및 기본 속성 공식적으로 Q-기능은 다음과 같이 정의된다.
Q ( x ) = 1 2 π ∫ x ∞ 생략하다 ( − u 2 2 ) d u . {\displaystyle Q(x)={\frac {1}{\sqrt {2\pi }\int_{x}^{\inflt }\exp \left(-{\frac {u^{2}}\오른쪽)\,du.} 그러므로,
Q ( x ) = 1 − Q ( − x ) = 1 − Φ ( x ) , {\displaystyle Q(x)=1-Q(-x)=1-\Phi(x)\,\!,} 여기서 φ x {\displaystyle \Phi (x)} 표준 가우스 분포의 누적 분포 함수 다
Q-함수는 다음 과 같이[2] 에러함수 또는 보완 에러함수로 표현할 수 있다.
Q ( x ) = 1 2 ( 2 π ∫ x / 2 ∞ 생략하다 ( − t 2 ) d t ) = 1 2 − 1 2 에프 ( x 2 ) -또는- = 1 2 에르프크 ( x 2 ) . {\displaystyle {\begin}Q(x)&={\frac {1}{1}{1}{1}{2}}: 왼쪽({\frac {2}\pi }}\int _{x/{\sqrt{2}}:}^{\put \left(-t^{2}\rig)\,d\right)\cright)\cright)\cright)\ \&={\frac {1}{2}}-{\frac {1}{1}:{2}}\propername {erf} \left\frac}{x}{\sqrt{2}}\오른쪽) ~~{\text{ -or-}\\&={\frac {1}{1}:{2}}\\frcname {erfc} \left\frac}{x}{\sqrt{2}}}\오른쪽). \end{정렬}}} 크레이그의 공식으로 알려진 Q-함수의 다른 형태는 발견자의 뒤에 다음과 같이 표현된다.[4]
Q ( x ) = 1 π ∫ 0 π 2 생략하다 ( − x 2 2 죄를 짓다 2 θ ) d θ . {\displaystyle Q(x)={\frac {1}{\pi }\int _{0}^{0}{0}^{\pi }}}}}\exp \left(-{\frac {x^{2}}:{2}\sin ^{}\ta }d\ta.}}}} 이 식은 x 의 양의 값에만 유효하지만, Q (x ) = 1 - Q (-x )와 함께 사용하여 음의 값에 대한 Q(x )를 얻을 수 있다. 통합의 범위가 고정적이고 유한하다는 점에서 이 형식이 유리하다.
크레이그의 공식은 이후 베나드(2020)[5]
Q ( x + y ) = 1 π ∫ 0 π 2 생략하다 ( − x 2 2 죄를 짓다 2 θ − y 2 2 cas 2 θ ) d θ , x , y ⩾ 0. {\displaystyle Q(x+y)={\frac {1}{\pi }}\int _{0}^{\frac {\pi }{2}}\exp \left(-{\frac {x^{2}}{2\sin ^{2}\theta }}-{\frac {y^{2}}{2\cos ^{2}\theta }}\right)d\theta ,\quad x,y\geqslant 0.} 한계 및 근사치 Q 기능은 기본 기능이 아니다 . 그러나 where x {\displaystyle \pi (x)} [6] ( x 1 + x 2 ) ϕ ( x ) < Q ( x ) < ϕ ( x ) x , x > 0 , {\displaystyle \left\frac {x}{1+x^{2 }}}\phi(x)\phi(x)<{\frac {\phi(x)}{x}}}},\qquad x>0,} large x 에 대해 점점 더 빡빡해지고 종종 유용하다. 대체 v =u 2 /2를 사용하여 상한은 다음과 같이 도출된다. Q ( x ) = ∫ x ∞ ϕ ( u ) d u < ∫ x ∞ u x ϕ ( u ) d u = ∫ x 2 2 ∞ e − v x 2 π d v = − e − v x 2 π x 2 2 ∞ = ϕ ( x ) x . {\displaystyle Q(x)=\int _{x}^{\infty }\phi (u)\,du<\int _{x}^{\infty }{\frac {u}{x}}\phi (u)\,du=\int _{\frac {x^{2}}{2}}^{\infty }{\frac {e^{-v}}{x{\sqrt {2\pi }}}}\,dv=-{\biggl . }}{\frac{e^{-v}{x{\sqrt{2\pi }}}{{\biggr}}{\biggr}{\frac{x^{2}}:{}}={\frac {\pi(x)}}}}}. } 마찬가지로 ϕu u ϕ ( u {\displaystyle \pi '(u)=-u\pi(u)} quotient rule 을 사용하여 ( 1 + 1 x 2 ) Q ( x ) = ∫ x ∞ ( 1 + 1 x 2 ) ϕ ( u ) d u > ∫ x ∞ ( 1 + 1 u 2 ) ϕ ( u ) d u = − ϕ ( u ) u x ∞ = ϕ ( x ) x . {\displaystyle \left(1+{\frac {1}{x^{2}}}\right)Q(x)=\int _{x}^{\infty }\left(1+{\frac {1}{x^{2}}}\right)\phi (u)\,du>\int _{x}^{\infty }\left(1+{\frac {1}{u^{2}}}\right)\phi (u)\,du=-{\biggl . }}{\frac {\fi(u)}{u}}{{\biggr }_{x}^{\inflt }={\frac {\phi(x)}{x}}}. } Q (x )에 대한 해결은 하한을 제공한다.상한 기하 평균 은 displaystyle Q(x)} . Q ( x ) ≈ ϕ ( x ) 1 + x 2 , x ≥ 0. {\displaystyle Q(x)\약간 {\frac {\phi(x)}{\sqrt {1+x^{2 }}},\qquad x\geq 0.} Q x {\displaystyle Q(x)} Q ~ ( x ) = ϕ ( x ) ( 1 − a ) x + a x 2 + b . {\displaystyle {\tilde{Q}}(x)={\frac {\phi(x)}{{(1-a)x+a{\sqrt{x^{2}+b}}}}}}. } x ≥ 0 {\displaystyle x\geq } , 최대 0.344 {\ displaystyle a=0.344} 5 .334} ) 최적 마찬가지로, 최대 절대 상대 오차 0.27%인 0.339 (\displaystyle a=0.339}) 5 (\displaystyle b=5 ( 마지막으로, 최대 절대 상대 오차가 1.17 % = display displaystyle /\pi } 및 2 display displaystyle 2\pi } Q ( x ) ≤ e − x 2 2 , x > 0 {\displaystyle Q(x)\leq e^{-{\frac {x^{2}}:},\qquad x>0} Q ( x ) ≤ 1 4 e − x 2 + 1 4 e − x 2 2 ≤ 1 2 e − x 2 2 , x > 0 {\displaystyle Q(x)\leq {\tfrac {1}{4}}e^{-x^{2}}+{\tfrac {1}{4}}e^{-{\frac {x^{2}}{2}}}\leq {\tfrac {1}{2}}e^{-{\frac {x^{2}}{2}}},\qquad x>0} Q ( x ) ≈ 1 12 e − x 2 2 + 1 4 e − 2 3 x 2 , x > 0 {\displaystyle Q(x)\cHB {1}{12}e^{-{\frac {x^{2}}:}+{\frac {1}{1}{1}{4}e^{{}{{3}}}{3}x^,\qquad x>0} 위의 내용은 Tanash & Rihonen(2020)에 의해 일반화되었는데,[8] Q x ) {\displaystyle (x)} Q ~ ( x ) = ∑ n = 1 N a n e − b n x 2 . {\displaystyle {\tilde{Q}}(x)=\sum _{n=1}^{{n}a_{n}e^{-b_{n}x^{2}. } In particular, they presented a systematic methodology to solve the numerical coefficients { ( a n , b n ) } n = 1 N {\displaystyle \{(a_{n},b_{n})\}_{n=1}^{N}} minimax approximation or bound: Q ( x ) ≈ Q ~ ( x ) {\displaystyle Q(x)\approx {\tilde {Q}}(x)} Q ( x ) ≤ Q ~ ( x ) {\displayst yle Q(x)\leq {\tilde {Q}}(x)} Q ( x ) ≥ Q ~ ( x ) {\displaystyle Q(x)\geq {\tilde {Q}}(x)} x ≥ 0 {\displaystyle x\geq 0} N = 20 {\displaystyle N=20} 2.831 ⋅ 10 − 6 {\displaystyle 2. 831\cdot 10^{-6}, 1 .416 ⋅ 10 6 {\ displaystyle .416\cdot 10^{-6} . 지수 25 {\displaystyle \{(a_{n},b_{n {n=1}^{ N}}} {( n b ) [9] X [[ 0 ∞ {\displaystyle x\in[0,\infit )} Q x ){\displaystyle Q(x)} A } {\displaystystyle \{A,B\}}} [10] f ( x ; A , B ) = ( 1 − e − A x ) e − x 2 B π x ≈ 에르프크 ( x ) . {\displaystyle f(x;A,B)={\frac {\좌측(1-e^{-Ax}\우측)e^{-x^{-x^{2}}:{B{\\sqrt {\pi }}}}}}}}관련 \erfc(x\우측) } [0 R ] {\displaystyle f(x;A,B)} , erfc x displaystyle operatorname erfc}(x 0,R] { A , B } = 아그 분 { A , B } 1 R ∫ 0 R f ( x ; A , B ) − 에르프크 ( x ) d x . {\displaystyle \{A,B\}={\underset {\A,B\}}{\arg \min }{\frac {1}{R}\int _{0}^}f(x;A,B)-\operatorname {erfc}(x) dx.} Using R = 20 {\displaystyle R=20} { A , B } = { 1.98 , 1.135 } , {\displaystyle \{A,B\}=\{1.98,1.135\},} ∀ x ≥ 0. {\displaystyle \forall x\geq 0.} 이러한 값을 대체하고 위의 Q ( x {\displaystyle Q(x)} erfc ( x {\displaystyle \operatorname {erfc}(x)} Q ( x ) ≈ ( 1 − e − 1.98 x ) e − x 2 2 1.135 2 π x , x ≥ 0. {\displaystyle Q(x)\cHB(약 1-e^{-1.98x}\right)e^{-{-{\frac{x^{2}}:{1.135{\sqrt{2\pi}}}}}}}}{1.135{2\sqrt{2\x\geq 0.} 위의 '카라지안니디스-'에 대해서도 대체 계수를 사용할 수 있다. 특정 용도에 대한 정확도를 맞춤화하거나 엄격한 바운드로 변환하기 위한 Lioumpas 근사치.[11] 로페즈-베니테스 & 카사데발(2011)[12] 인수 [ 0 ) {\displaystyle x\in [0,\infit )} 대한 x ){\displaystyle Q(x)} Q ( x ) ≈ e − a x 2 − b x − c , x ≥ 0. {\displaystyle Q(x)\ 관련 e^{-ax^{2}-bx-c},\qquad x\geq 0.} The fitting coefficients ( a , b , c ) {\displaystyle (a,b,c)} a = 0.3842 {\displaystyle a=0.3842} b = 0.7640 {\displaystyle b=0.7640} c = 0.6964 {\displaystyle c=0.6964} x ∈ [ 0 , 20 ] {\displaystyle x\in [0,20 x ∈ 0 , 20 ] {\displaystyle a=0.4920 0.2887 {\displaystyle b=0.2887 c 1893 {\ displaystystyle c=1. 1893 }) . 이 근사치는 정확성과 분석적 추적성 사이의 양호한 트레이드오프와 같은 일부 이점을 제공한다(예를 들어 x {\displaystyle (x)} 역 Q역 Q-함수는 역오차함수 와 관련될 수 있다.
Q − 1 ( y ) = 2 e r f − 1 ( 1 − 2 y ) = 2 e r f c − 1 ( 2 y ) {\displaystyle Q^{-1(y)={\sqrt{2}}\\mathrm {erf}^{-1}(1-2y)={\sqrt{2}}\\mathrm {erfc}^{-1}(2y)} Q 1 {\displaystyle ^{-1}(y)} 일반적으로 dB 로 표현되며 일반적으로 Q-요인 (Q-factor):
Q - f a c t o r = 20 통나무를 하다 10 ( Q − 1 ( y ) ) d B {\displaystyle \mathrm {Q{\text{-}factor} =20\log _{10}\! \left(Q^{-1}(y)\right)\! ~\mathrm {dB} } 여기서 y 는 분석 중인 디지털 변조 신호의 비트 오류 속도(BER)이다. 예를 들어, 가우스 노이즈가 첨가된 QPSK 의 경우, 위에서 정의한 Q-요인은 y 와 동일한 비트 오류율을 생성하는 신호 대 잡음비 의 dB 값과 일치한다.
가치 Q-함수는 표에 잘 표시되어 있으며, R 과 같은 대부분의 수학 소프트웨어 패키지와 파이썬 , MATLAB , 매티매티카 에서 이용할 수 있는 패키지에서 직접 계산할 수 있다. Q-함수의 일부 값은 참조를 위해 아래에 제시되어 있다.
Q (0.0) 0.500000000 1/2.0000 Q (0.1) 0.460172163 1/2.1731 Q (0.2) 0.420740291 1/2.3768 Q (0.3) 0.382088578 1/2.6172 Q (0.4) 0.344578258 1/2.9021 Q (0.5) 0.308537539 1/3.2411 Q (0.6) 0.274253118 1/3.6463 Q (0.7) 0.241963652 1/4.1329 Q (0.8) 0.211855399 1/4.7202 Q (0.9) 0.184060125 1/5.4330
Q (1.0) 0.158655254 1/6.3030 Q (1.1) 0.135666061 1/7.3710 Q (1.2) 0.115069670 1/8.6904 Q (1.3) 0.096800485 1/10.3305 Q (1.4) 0.080756659 1/12.3829 Q (1.5) 0.066807201 1/14.9684 Q (1.6) 0.054799292 1/18.2484 Q (1.7) 0.044565463 1/22.4389 Q (1.8) 0.035930319 1/27.8316 Q (1.9) 0.028716560 1/34.8231
Q (2.0) 0.022750132 1/43.9558 Q (2.1) 0.017864421 1/55.9772 Q (2.2) 0.013903448 1/71.9246 Q (2.3) 0.010724110 1/93.2478 Q (2.4) 0.008197536 1/121.9879 Q (2.5) 0.006209665 1/161.0393 Q (2.6) 0.004661188 1/214.5376 Q (2.7) 0.003466974 1/288.4360 Q (2.8) 0.002555130 1/391.3695 Q (2.9) 0.001865813 1/535.9593
Q (3.0) 0.001349898 1/740.7967 Q (3.1) 0.000967603 1/1033.4815 Q (3.2) 0.000687138 1/1455.3119 Q (3.3) 0.000483424 1/2068.5769 Q (3.4) 0.000336929 1/2967.9820 Q (3.5) 0.000232629 1/4298.6887 Q (3.6) 0.000159109 1/6285.0158 Q (3.7) 0.000107800 1/9276.4608 Q (3.8) 0.000072348 1/13822.0738 Q (3.9) 0.000048096 1/20791.6011 Q (4.0) 0.000031671 1/31574.3855
높은 차원으로 일반화 Q 기능은 더 높은 차원으로 일반화할 수 있다.[13]
Q ( x ) = P ( X ≥ x ) , {\displaystyle Q(\mathbf {x} )=\mathb {P}(\mathbf {X} \geq \mathbf {x}),} where X ∼ N ( 0 , Σ ) {\displaystyle \mathbf {X} \sim {\mathcal {N}}(\mathbf {0} ,\,\Sigma )} Σ {\displaystyle \Sigma } x = γ Σ l ∗ {\displaystyle \mathbf {x} =\gamma \Sigma \mathbf {l} ^{*}} r l ∗ 0 {\ displaystyle \mathbf {l} ^{*}}\mathbf {0} 0 {\displaystyle \gamma 0 그럼에도 불구하고 Q-함수는 임의적으로 잘 추정 될 수 있으며, as {\displaystyle \gamma ( [14] [15]
참조 ^ Q-기능 , cnx.org ^ a b 2009년 3월 25일 웨이백 머신 에 보관 된 Q 기능의 기본 속성 ^ 정규 분포함수 - Wolfram MathWorld의 분포 ^ Craig, J.W. (1991). "A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations" (PDF) . MILCOM 91 - Conference record . pp. 571–575. doi :10.1109/MILCOM.1991.258319 . ISBN 0-87942-691-8 S2CID 16034807 . ^ Behnad, Aydin (2020). "A Novel Extension to Craig's Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis". IEEE Transactions on Communications . 68 (7): 4117–4125. doi :10.1109/TCOMM.2020.2986209 . S2CID 216500014 . ^ a b Borjesson, P.; Sundberg, C.-E. (1979). "Simple Approximations of the Error Function Q(x) for Communications Applications". IEEE Transactions on Communications . 27 (3): 639–643. doi :10.1109/TCOM.1979.1094433 . ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). "New exponential bounds and approximations for the computation of error probability in fading channels" (PDF) . IEEE Transactions on Wireless Communications . 24 (5): 840–845. doi :10.1109/TWC.2003.814350 . ^ Tanash, I.M.; Riihonen, T. (2020). "Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials". IEEE Transactions on Communications . 68 (10): 6514–6524. arXiv :2007.06939 doi :10.1109/TCOMM.2020.3006902 . S2CID 220514754 . ^ Tanash, I.M.; Riihonen, T. (2020). "Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]" . Zenodo . doi :10.5281/zenodo.4112978 . ^ Karagiannidis, George; Lioumpas, Athanasios (2007). "An Improved Approximation for the Gaussian Q-Function" (PDF) . IEEE Communications Letters . 11 (8): 644–646. doi :10.1109/LCOMM.2007.070470 . S2CID 4043576 . ^ Tanash, I.M.; Riihonen, T. (2021). "Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function". IEEE Communications Letters . 25 (5): 1468–1471. arXiv :2101.07631 doi :10.1109/LCOMM.2021.3052257 . ^ Lopez-Benitez, Miguel; Casadevall, Fernando (2011). "Versatile, Accurate, and Analytically Tractable Approximation for the Gaussian Q-Function" (PDF) . IEEE Transactions on Communications . 59 (4): 917–922. doi :10.1109/TCOMM.2011.012711.100105 . S2CID 1145101 . ^ Savage, I. R. (1962). "Mills ratio for multivariate normal distributions" . Journal of Research of the National Bureau of Standards Section B . 66 (3): 93–96. doi :10.6028/jres.066B.011 Zbl 0105.12601 . ^ Botev, Z. I. (2016). "The normal law under linear restrictions: simulation and estimation via minimax tilting". Journal of the Royal Statistical Society, Series B . 79 : 125–148. arXiv :1603.04166 Bibcode :2016arXiv160304166B . doi :10.1111/rssb.12162 . S2CID 88515228 . ^ Botev, Z. I.; Mackinlay, D.; Chen, Y.-L. (2017). "Logarithmically efficient estimation of the tail of the multivariate normal distribution". 2017 Winter Simulation Conference (WSC) . IEEE. pp. 1903–191. doi :10.1109/WSC.2017.8247926 . ISBN 978-1-5386-3428-8 S2CID 4626481 . 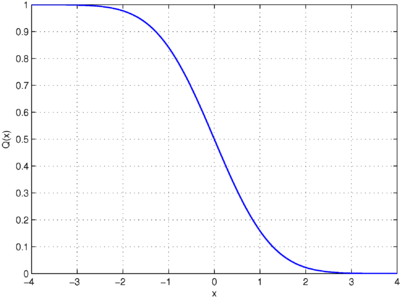


 (가) 평균
(가) 평균  (
(
 ,
, 



 .
. 




























 적절한 선택에 대해 보여준 카라지안니디스 & 리움파스(2007)에 의해 주어진다
적절한 선택에 대해 보여준 카라지안니디스 & 리움파스(2007)에 의해 주어진다

 [0
[0
![{\displaystyle [0,R]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ea1a7293db142452ce72c16d8f7c427fccf434c)










![{\displaystyle x\in [0,20]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/385e4b36c43d3baf83dd06f9430503dc5dbaed18)


 최소화한다
최소화한다












