상호성(전기 네트워크)

전기 네트워크의 상호성은 두 지점에서 전압과 전류를 관련짓는 회로의 특성입니다.상호성 정리는 두 번째 지점의 전압으로 인한 회로의 한 지점의 전류가 첫 번째 지점의 동일한 전압으로 인한 두 번째 지점의 전류와 동일하다는 것을 나타냅니다.상호성 정리는 거의 모든 패시브네트워크에 유효합니다.상호성 정리는 전자기학의 보다 일반적인 상호성 원리의 특징이다.

묘사

$전류$일 경우 $\$ I_${\text{$$A}}}$이$($가) 포트 A에 주입되면 V $(\$가 전압을 생성합니다.$B$ 포트 B $및{\displaystyle {}_{}}$의 {\$displaystyle I_{\text}$$A}}}$을(를) 포트 B에 삽입하면 $B$가 $생성$됩니다.{ \ $text$}$포트$ A에 B$}}$이(가) 있으면 네트워크는 상호적이라고 합니다.마찬가지로 상호성은 전압을 $인가$하는 V $(\$의 이중 상황으로 정의할 수 있습니다.$A$ 포트 A에서 $전류{\displaystyle {}_{}}$를 생성합니다(\$displaystyle I_{\text{$$포트$ B 및$$ ${\displaystyle V_{}}$A의 B$}}$ {\$displaystyle V_{\text${\text$}$$A}})$ 포트$$ B에서 $전류{\displaystyle {}_{}}$를 생성합니다(\$displaystyle I_{\text{$$포트$ ^[1]A에서 B$}}.$일반적으로 패시브 네트워크는 상호적입니다.이상적인 캐패시턴스, 인덕턴스(상호 인덕턴스 포함) 및 저항(즉, 선형 및 쌍방향)으로 구성된 네트워크는 모두 ^[2]상호적입니다.단, 비호환적인 패시브컴포넌트는 존재합니다.강자성 물질을 포함하는 모든 구성 요소는 비호환일 가능성이 높습니다.비호환적으로 의도적으로 설계된 수동 구성 요소의 예로는 순환기 및 ^[3]절연체가 있습니다.

상호 네트워크의 전송 함수는 z-파라미터, y-파라미터 또는 s-파라미터 행렬로 표현될 경우 주 대각선에 대해 대칭이라는 특성이 있습니다.비대칭 매트릭스는 비호환 네트워크를 의미합니다.대칭 행렬은 대칭 네트워크를 ^[4]의미하지 않습니다.

네트워크의 일부 파라미터화에서는 대표 매트릭스가 상호 네트워크에 대해 대칭적이지 않습니다.일반적인 예로는 h-파라미터와 ABCD-파라미터가 있지만 모두 파라미터에서 계산할 수 있는 다른 상호성 조건이 있습니다.h 파라미터의 경우 조건은 $h{\displaystyle {}_{}}$ ${\displaystyle {12}_{}}$ ${\displaystyle =}$ - h $({$}=-$h_{21$$})$이고 ABCD 파라미터의 경우 ${\displaystyle A}$D - ${\displaystyle B}$ ${\displaystyle \mathrm{C}}$ $=$ 1({$displaystyle AD-BC=1$입니다. 이러한 표현은 동일한 열 벡터에 전압과 전류를 혼합하므로 전치된 ^[5]단위도 없습니다.

예

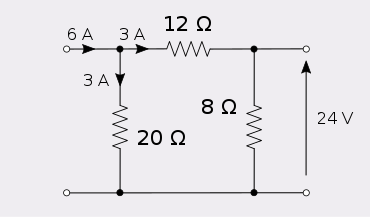
비대칭 저항 감쇠기를 사용하여 상호성의 예를 제시할 수 있다.대칭 네트워크는 상당히 자명하게 상호적이기 때문에 비대칭 네트워크가 그 예로서 선택된다.

이 네트워크의 포트 1에 6A를 주입하면 포트 2에서 24V가 생성됩니다.

포트 2에 6A를 주입하면 포트 1에서 24V가 생성됩니다.

따라서 네트워크는 상호적입니다.이 예에서는 전류를 주입하지 않는 포트는 개방된 상태로 유지됩니다.이는 0 전류를 인가하는 전류 발생기가 개방 회로이기 때문입니다.한편, 전압을 인가해 전류를 측정하려고 하면 전압이 인가되지 않은 포트가 단락됩니다.이는 0V를 인가하는 전압 발생기가 단락 회로이기 때문입니다.

증명

전기 네트워크의 상호성은 로렌츠 상호성의 특별한 경우이지만 네트워크 이론에서 더 직접적으로 증명될 수도 있습니다.이 증명은 어드미턴스 매트릭스의 관점에서 2노드 네트워크에 대한 상호성을 나타내고 유도 인수에 의해 임의의 수의 노드를 가진 네트워크에 대한 상호성을 나타냅니다.선형 네트워크는 노드 분석을 통해 일련의 선형 방정식으로 나타낼 수 있습니다.이 방정식은 어드미턴스 ^[6]행렬의 형태로 표현될 수 있다.

$(\displaystyle \ bmatrix \I_{1}\\I_{2}\\vdots\\I_{n}\end{bmatrix}}=(begin{bmatrix})Y_{11}&Y_{12}&\cdots&Y_{1n}\\Y_{214}&Y_{22}&\cdots&Y_{2n}\vdots&\vdots&Y_{n1}&\cdots&Y_{n}\end{bmatrix}{\begin{matrix}_V}$

어디에

${\displaystyle I_{}}$ k$(\$는 제너레이터에 의해 노드 k에 주입된 전류입니다.

${\displaystyle V_{}}$k({$displaystyle V_{k})$는 노드 k에서의 전압입니다.

${\displaystyle Y_{}}$ ${\displaystyle j_{}}$k(\$displaystyle Y_{jk})($j kk)는 노드 j와 노드 k 사이에 연결된 어드미턴스의 음수입니다.

${\displaystyle Y_{}}$ $(\$는 노드 k에 연결된 어드미턴스의 합계입니다.

네트워크가 수동적인 쌍방향 요소로 구성되어야 하는 경우,

${\displaystyle Y_{jk}=Y_{kj}}$

노드 j와 k 사이에 연결된 어드미턴스는 노드 k와 j 사이에 연결된 어드미턴스와 동일한 요소이기 때문이다.따라서 행렬은 ^[7]대칭입니다.n$$ $2$인 $경우{\displaystyle }$(\$style$ n$=$2) 매트릭스는 다음과 같이 감소합니다.

$]$$I_{1}\\I_{2}\end{bmatrix}=begin{bmatrix}$$Y_{11}&Y_{12}\\$$Y_{212}&Y_{22}\end{bmatrix}{\begin{bmatrix}V_{1}\V_{2}\end{bmatrix$

어느 것에서 그것 that, 볼 수 있다.

Y12)나는 1V 2V1=0{\displaystyle Y_{12}=\left.{\frac{I_{1}}{V_{2}}}\right _{V_{1}=0}}과

${\displaystyle Y_{21}=\left.{\frac{I_{2}}{V_{1}}}\right _{V_{2}=0}년.}$

하지만 Y12일 이후)Y21{\displaystyle Y_{12}=Y_{21}}then,.

${\displaystyle \left.{\frac{I_{1}}{V_{2}}}\right}_{V_{1}=0 =\left.{\frac{I_{2}}{V_{1}}}_{V_{2}=0}\right}$

어느 호혜 주의 상태가 동의어이다.말로, 한 포트의 전류 전압을 다른 술집의 비율은 같은 비율이 항구와 측정 상호 교환할 수 있고 있다.따라서 호혜 n의 경우는 x2{\displaystyle n=2}.[8]입증된다.

임의의 크기의 행렬의 경우 매트릭스의 명령 노드 제거를 통해 줄일 수 있다.그다 노드를 제거하여 끝나고, 새로운 어드미턴스 매트릭스를 form, 것이다.

${\displaystyle{\begin{bmatrix}(Y_{11}Y_{ss}-Y_{s1}Y_{1})&.(Y_{12}Y_{ss}-Y_{s2}Y_{1})&(Y_{13}Y_{ss}-Y_{s 3 언제라도}Y_{1})&\cdots \\(Y_{21}Y_{ss}-Y_{s1}Y_{2초씩})&(Y_{22}Y_{ss}-Y_{s2}Y_{2초씩})&(Y_{23}Y_{ss}-Y_{s 3 언제라도}Y_{2초씩})&\cdots \\(Y_{31일}Y_{ss}-Y_{s1}Y_{3초})&(Y_{32}Y_{ss}-Y_{s2}Y_{3초})&(Y_{33}Y_{ss}-Y_{s 3 언제라도}Y_{3초})&\cdots \\\cdots, \cdots &, \cdots &, \cdots \end{bmatrix}}&}.$

이 새로운 행렬도 대칭임을 알 수 있다.2×2 대칭 매트릭스만 해당 2개의 노드를 포함할 때까지 노드를 계속 제거할 수 있습니다.이 행렬은 대칭이기 때문에 한 노드가 다른 노드에서 측정된 전압 및 전류에 의해 구동될 때 임의의 크기의 행렬에 상호성이 적용된다는 것이 입증되었습니다.메시 분석의 임피던스 행렬을 사용하는 유사한 프로세스는 한 노드가 전류에 의해 구동되고 다른 ^[9]노드에서 전압이 측정되는 상호성을 보여줍니다.

레퍼런스

참고 문헌

• 미국, Bakshi; A.V., Electrical Networks, Technical Publications, 2008 ISBN8184314647.
• Guillemin, Ernst A., 입문회로가론, 뉴욕: John Wiley & Sons, 1953 OCLC 535111
• Kumar, K. S. S. Suresh, 전기회선 및 네트워크, Pearson Education India, 2008 ISBN 8131713903.
• Harris, Vincent G., "마이크로웨이브 페라이트 및 응용 프로그램", 14인치, Mailadil T.장.Sebastian, Rick Ubic, Heli Jantunen, Microw Materials and Applications, John Wiley & Sons, 2017 ISBN 1119208521.
• Zhang, Kequian; Li, Dejie, 전자레인지 및 광일렉트로닉스의 전자기 이론, Springer Science & Business Media, 2013 ISBN 3662035537.