칠거울

원자물리학에서, 박리된 거울(또는 박리된 원자 거울 또는 프레스넬 회절 거울)은 방목 발생각에서 오는 중성 입자(atoms)의 정반사를 위해 설계된 원자 거울의 일종이다.입자의 표면으로의 평균 흡인력을 줄이고 반사율을 높이기 위해 이 표면은 좁은 능선을 가지고 있다.^[1]

비산 원자 거울의 반사율

박리거울의 파동 양자반사의 효율성에 대한 다양한 추정치가 문헌에서 논의되었다.모든 추정치는 반사된 원자의 파동 특성에 관한 드 브로글리 이론을 명시적으로 사용한다.

반 데르 발스 힘의 스케일링

능선은 표면으로부터의 양자반사를 강화하여 원자의 표면으로의 반데르발스 흡인력의 유효$$ 상수 ${\$를 감소시킨다.그러한 해석은 반사율의 추정으로 이어진다.

${\$$\left({\frac {\ell}{L}C,\!$$~K\sin(\theta )\right$

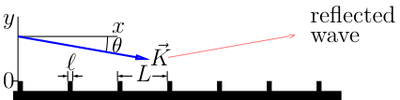
where ${\displaystyle ~\ell ~}$ is width of the ridges, ${\displaystyle ~L~}$ is distance between ridges, ${\displaystyle \displaystyle ~\theta ~}$ is grazing angle, and ${\displaystyle ~K=mV/\hbar ~}$ is wavenumber and ${\displaystyle ~r_{0}(C,k)~}$ is coeffi정상 발생 시 평탄한 표면에서$$ wavenumber ${\displaystyle k}$ ${\$이(가) 있는 원자를 반사하는 cient.이러한 추정치는 ${\displaystyle L}$ ${\$ 기간의 증가 시 반사율의 향상을 예측한다$.$ 이 추정치는 $K{\displaystyle }$ ${\displaystyle L}$ ${\displaystyle \theta {}^{}}$ ${\displaystyle 2}$ ${\displaystyle {}^{}}$ 1 ${\displaystyle KL\!$$~\theta ^{2}\ll 1$ 함수 ${\displaystyle r{}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ $displaystyle ~r_{0}~}$의 근사치(적합치)는 양자 반사를 참조하십시오$.$

제노 효과로 해석

큰 $주기$의 L ${\displaystyle L}$이(가) 있는 좁은 굴곡의 경우, 굴곡은 단지 파형의 일부를 막는다$.$그렇다면 드 브로글리 파동의 프레넬 회절^[2][3], 즉 제노 효과의 관점에서 해석할 수 있는데,^[4] 그러한 해석은 반사율을 추정하게 된다.

$displaystyle ~\displaystyle r\$$~K\!~~L}\\theta \오른쪽$

${\displaystyle {\displaystyle 여기}}$서 방목각 {${\displaystyle$~\$theta$~}은$$(는) 작아야 한다.이 추정치는 ${\displaystyle 주기}$ L ${\$의 감소 시 반사율의 향상을 예측한다$.$ 이 추정치는 ${\displaystyle \ell }$/ ${\displaystyle L}$ ${\displaystyle \ll }$ ${\displaystyle 1}$ ${\$ 1$~}$을 요구한다$.$

기본 한계

효율적인 미러의 경우 위의 두 추정치 모두 높은 반사율을 예측해야 한다.이는 능선과 주기 $L{\displaystyle }$ ${\displaystyle$ $\$$ell$$}$의 둘 $다$의 축소를 의미한다$.$ 능선의 폭은 원자의 크기보다 작을 수 없다. 이는 구불구불한 미러의 성능 한계를 설정한다.^[5]

박리 미러 적용

어떤 업적이 언급될 수 있지만, 구식 거울은 아직 상용화되지 않았다.박리된 원자 거울의 반사율은 평평한 표면의 반사율보다 더 좋은 크기 순서가 될 수 있다.원자 홀로그램으로 옻칠한 거울의 사용이 증명되었다.시미즈나 후지타의 작품에서 원자 홀로그래피는 원자 거울을 통해 SiN₄ 필름에 착상된 전극을 통해, 또는 어쩌면 원자 거울 그 자체로서도 달성된다.^[6]

또한, 거울은 가시광선을 반사할 수 있지만,^[5] 광파의 경우, 평평한 표면보다 성능이 더 좋지 않다.타원형 제거 거울은 서브크로미터 분해능(원자 나노스코프)을 갖는 원자 광학 시스템의 초점 요소로 제안된다.

참고 항목

• 원자 거울
• 양자반사
• 원자 나노스코프
• 제노 효과
• 물질파

참조