로토르디나믹스
Rotordynamics이 기사의 리드 섹션에는 기사에 포함되지 않은 정보가 포함되어 있다. (2022년 1월)(이과 시기 |
로터역학(Rotordynamics)은 회전 구조물의 거동 및 진단과 관련된 응용 역학의 전문 분야다. 제트엔진과 증기터빈에서 자동차엔진, 컴퓨터디스크 저장장치에 이르는 구조물의 거동을 분석하는 데 흔히 사용된다. 가장 기본적인 수준에서 로터 역학은 베어링에 의해 지지되고 단일 축을 중심으로 회전하는 내부 현상의 영향을 받는 하나 이상의 기계적 구조물(로터)과 관련된다. 지지 구조는 스테이터라고 불린다. 회전 속도가 증가함에 따라 진동의 진폭은 임계 속도라고 하는 최대값을 통과하는 경우가 많다. 이 진폭은 일반적으로 회전 구조의 불균형에 의해 흥분된다; 일상적인 예로는 엔진 밸런스와 타이어 밸런스를 포함한다. 이러한 임계 속도에서 진동의 진폭이 과도하면 치명적인 고장이 발생한다. 이 외에도 터보 기계의 내부 구성과 관련된 불안정성이 자주 발생하며, 이를 반드시 교정해야 한다. 대형 로터를 설계하는 기술자들의 주요 관심사다.
회전 기계는 그 과정에 관여하는 메커니즘의 구조에 따라 진동을 발생시킨다. 기계의 어떤 결함도 진동 신호를 증가시키거나 흥분시킬 수 있다. 불균형으로 인한 기계의 진동 거동은 회전하는 기계의 주요 측면 중 하나로서, 설계하는 동안 상세히 연구되고 고려되어야 한다. 회전 기계를 포함한 모든 물체는 물체의 구조에 따라 자연적인 주파수를 나타낸다. 회전 기계의 임계 속도는 회전 속도가 자연 주파수와 일치할 때 발생한다. 자연 주파수가 처음 만나는 가장 낮은 속도를 첫 번째 임계 속도라고 하지만 속도가 증가함에 따라 자연 주파수의 배수인 추가 임계 속도가 보인다. 따라서, 회전 불균형과 불필요한 외부 힘을 최소화하는 것은 공명을 일으키는 전체적인 힘을 줄이는 데 매우 중요하다. 진동이 공명할 때 회전하는 기계를 설계할 때 주된 관심사가 되어야 하는 파괴적인 에너지를 생성한다. 여기서 목표는 임계치에 가까운 작동을 피하고 가속 또는 감속 시 이를 안전하게 통과하는 것이어야 한다. 이러한 측면을 무시하면 장비의 손실, 과도한 기계 마모, 수리할 수 없는 치명적인 파손 또는 심지어 인명 손실로 이어질 수 있다.
그 기계의 실제 역학은 이론적으로 모델링하기 어렵다. 계산은 다양한 구조적 구성요소(펄프 매개변수 모델), 수치로 모델을 풀 때 얻은 방정식(Rayleigh-Ritz 방법) 및 마지막으로 유한요소법(FEM)을 바탕으로 하며, 이는 자연주파수에 대한 기계의 모델링 및 분석을 위한 또 다른 접근방식이다. 분석 및 폐쇄형 자연주파수, 임계속도, 불균형 질량반응을 발생시킬 [1]수 있는 분산전달함수법 등 분석방법도 있다. 기계 프로토타입에서 공명의 정확한 주파수를 확인하기 위해 시험한 후 공명이 발생하지 않도록 재설계한다.
기본 원리
일정한 회전 속도 Ω으로 회전하는 축 대칭 로터에 대한 일반화된 매트릭스 형태의 운동 방정식은 다음과 같다.
여기서:
- M은 대칭 질량 행렬이다.
- C는 대칭 댐핑 매트릭스
- G는 스큐 대칭 자이로스코프 행렬이다.
- K는 대칭 베어링 또는 씰 강성 행렬이다.
- N은 예를 들어 원심원소 포함을 위한 편향의 자이로스코프 행렬이다.
여기서 q는 관성 좌표에서 로터의 일반화된 좌표이며 f는 강제 함수로서 보통 불균형을 포함한다.
자이로스코프 행렬 G는 스핀 속도 Ω에 비례한다. 위의 방정식에 대한 일반적인 해법은 스핀 속도에 따라 달라지는 복잡한 고유 벡터를 포함한다. 이 분야의 공학 전문가들은 캠벨 도표에 의존하여 이러한 해결책을 탐구한다.
방정식의 회전역학 시스템의 흥미로운 특징은 강성, 댐핑 및 질량의 비대각 항이다. 이러한 용어를 교차 결합 강성, 교차 결합 댐핑 및 교차 결합 질량이라고 한다. 양의 교차 결합 강성이 있을 때, 편향은 편향 방향과 반대되는 반작용력을 일으켜 하중을 반응하게 하고, 또한 양의 회전 방향의 반작용력을 발생시킨다. 이 힘이 사용 가능한 직접 댐핑 및 강성에 비해 충분히 크면 로터가 불안정해진다. 로터가 불안정할 경우, 일반적으로 심각한 고장을 방지하기 위해 기계를 즉시 정지시켜야 한다.
캠벨 도표
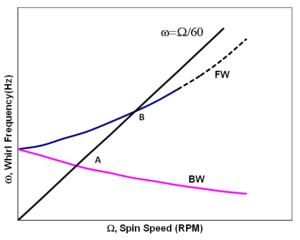
단순 로터 시스템의 "휘돌 속도도" 또는 "주파수 간섭도"라고도 하는 캠벨 도표가 오른쪽에 표시된다. 분홍색과 파란색 곡선은 각각 역회전(BW)과 전진회전(FW) 모드를 보여주는데, 회전 속도가 빨라질수록 분기한다. BW 주파수 또는 FW 주파수가 동기식 스핀 속도 라인과 A와 B 절에 의해 지시되는 스핀 속도 Ω과 같을 때, 로터의 응답은 피크를 나타낼 수 있다. 이것을 임계 속도라고 한다.
제프콧 로터
유럽의 드 라발 로터로도 알려진 제프콧 로터(Henry Homan Jeffcott의 이름을 딴 이름)는 이러한 방정식을 푸는 데 사용되는 단순화된 덩어리 매개변수 모델이다. 제프콧 로터는 실제 로터 역학을 반영하지 않을 수 있는 수학적 이상화다.
역사
로토르디나믹스의 역사는 이론과 실천의 상호작용으로 가득 차 있다. W. J. M. 랭킨은 1869년에 처음으로 회전축에 대한 분석을 수행했지만, 그의 모델은 적절하지 않았고 초임계 속도를 달성할 수 없다고 예측했다. 1895년에 던커리는 초임계 속도를 설명하는 실험 논문을 발표했다. 스웨덴의 엔지니어인 구스타프 드 라발은 1889년 증기 터빈을 초임계 속도로 운행했고, 커는 1916년 제2의 임계 속도에 대한 실험 증거를 보여주는 논문을 발표했다.
헨리 제프콧은 런던 왕립 협회의 의뢰로 이론과 실제의 충돌을 해결했다. 그는 현재 1919년 철학잡지에 고전으로 여겨지는 논문을 발표하여 안정적인 초임계 속도의 존재를 확인하였다. 아우구스트 퓌플은 1895년에 같은 결론을 많이 냈지만 역사는 그의 작품을 대부분 무시했다.
제프코트의 작업과 제2차 세계대전의 시작 사이에는 닐스 오토 미클스타드와[2] M. A. Prol의[3] 작업에서 불안정성과 모델링 기법의 작업이 많아 로터 분석을 위한 전송 매트릭스법(TMM)이 나왔다. 로토르디나믹스 분석에 오늘날 가장 보편적인 방법은 유한요소법이다.
현대의 컴퓨터 모델들은 다라 차일즈에서 인용한 인용문에서 "컴퓨터 코드의 예측의 품질은 기본 모델의 건전성과 분석가의 물리적 통찰력에 더 큰 관계가 있다"고 언급되어 왔다. 우수한 알고리즘이나 컴퓨터 코드는 나쁜 모델이나 공학적인 판단의 부족을 치료하지 못할 것이다."
F. 교수 넬슨은 로토르디나믹스의 역사에 대해 광범위하게 글을 썼으며, 이 부분의 대부분은 그의 작품에 기반을 두고 있다.
소프트웨어
방정식의 로터 다이나믹 시스템을 풀 수 있는 소프트웨어 패키지가 많다. 로터 다이나믹 특정 코드는 설계 목적에 더 유용하다. 이러한 코드는 베어링 계수, 측면 하중 및 로토다이내믹리스트만 필요로 하는 많은 항목들을 쉽게 추가할 수 있게 해준다. 비 회전자 동적 특정 코드는 FEA 해결기가 완전히 특징이며, 해결 기법에서 다년간 개발되었다. 비로터 동적 고유 코드는 로터 역학용으로 설계된 코드를 보정하는 데도 사용할 수 있다.
Rotordynamic 특정 코드:
- 다이나믹스 R4(알파-트란지트 주식회사) Ltd)[4] - 공간 시스템의 설계 및 분석을 위해 개발된 상용 소프트웨어
- AxSTREAM RotorDynamics, (SoftInWay)[5] - 로터 다이내믹스용 통합 소프트웨어 플랫폼으로, 빔 또는 2D 축대칭 요소에 대한 유한요소법을 사용하여 널리 사용되는 모든 로터 유형에 대해 횡방향, 비틀림 및 축방향 로터 다이내믹스가 가능하며, 자동화가 가능하다.
- Rotortest, (LAMAR - Campinas 대학교)[6] - 다양한 유형의 베어링 용액을 포함한 유한 요소 방법 기반 소프트웨어. LAMAR(Rotative of Rotating Machine) - Unicamp(Campinas University of Campinas)에서 개발.
- SAMCEF ROTOR[7] - 로터 시뮬레이션용 소프트웨어 플랫폼(LMS Samtech, A Siemens Business)
- MADIN(컨설팅 엔지니어 Klement)[8] - 다중 로터 및 기어(기판 및 하우징 포함)를 위한 상업용 유한 요소 횡방향, 비틀림, 축방향 및 결합형 솔버.
- MADIN 2000 (DELta JS Inc.)[9] - 다중 로터와 기어, 기초 및 케이싱용 상업용 조합 유한 요소(3D Timoshenko 빔) 횡방향, 비틀림, 축방향 및 결합형 솔버(3D Timoshenko 빔), 다양한 베어링(기름 필름, 스프링 댐퍼, 마그네틱, 롤링 요소)
- iSTRDYN(DynaTech Software LLC)[10] - 상용 2-D 축 대칭 유한 요소 해결사
- FEMRDIN(DynaTech Engineering, Inc.)[11] - 상용 1-D 축 대칭 유한 요소 해결사
- DyRoBeS(Eigen Technologies, Inc.)[12] - 상용 1-D 빔 요소 해결사
- RIMAP(RITEC)[13] - 상용 1-D 빔 요소 용해제
- XLRotor(회전 기계 분석, Inc.)[14] - 자기 베어링 제어 시스템 및 결합된 횡방향 비틀림 분석을 포함한 상용 1-D 빔 요소 용해제 Excel 스프레드시트를 사용한 로터 동적 모델링 및 분석을 위한 강력하고 빠르고 사용하기 쉬운 도구. VBA 매크로와 3D CAD 소프트웨어용 플러그인으로 간편하게 자동화
- ARMD(Rotor Bearing Technology & Software, Inc.)[15] - 전 세계적으로 연구자, OEM 및 최종 사용자가 사용하는 로토르디나믹스, 다중 지점 비틀림 진동, 유체 필름 베어링(유체역학, 정수 및 하이브리드) 설계, 최적화 및 성능 평가를 위한 상용 FEA 기반 소프트웨어.
- XLTRC2(텍사스 A&M)[16] - 학술용 1-D 빔 요소 해결사
- ComboRotor(Virginia University of Virginia)[17] - 산업용으로 광범위하게 검증된 임계 속도, 안정성 및 불균형 반응을 평가하는 다중 로터를 위한 결합된 유한 요소 횡방향, 비틀림, 축솔러
- MESWIR(Fluid-Flow Machine, 폴란드 과학 아카데미)[18] - 선형 및 비선형 범위 내의 로터 베어링 시스템 분석을 위한 학술용 컴퓨터 코드 패키지
- RoDAP(D&M Technology)[19] - 다중 로터, 기어 및 플렉시블 디스크(HDD)용 상업용 횡방향, 비틀림, 축방향 및 결합형 솔버
- 로터인사(ROTORINSA)[20] - 프랑스 공과대학(INSA-Lyon)에서 벤딩 시 로터의 정상 상태 동적 거동 분석을 위해 개발한 상용 유한요소 소프트웨어.
- COMSOL 다중물리학, Rotordynamics Module 추가 기능(Rotordynamics Module)[21]
- RAPPID - (Rotordynamic-Seal Research)[22] 로토다이내믹 계수 해결기를 포함한 상용 유한 요소 기반 소프트웨어 라이브러리(3D 솔리드 및 빔 요소)
참고 항목
참조
- Chen, W. J., Gunter, E. J. (2005). Introduction to Dynamics of Rotor-Bearing Systems. Victoria, BC: Trafford. ISBN 978-1-4120-5190-3.
{{cite book}}: CS1 maint: 여러 이름: 작성자 목록(링크) DyRoBeS 사용 - Childs, D. (1993). Turbomachinery Rotordynamics Phenomena, Modeling, & Analysis. Wiley. ISBN 978-0-471-53840-0.
- Fredric F. Ehrich, ed. (1992). Handbook of Rotordynamics. McGraw-Hill. ISBN 978-0-07-019330-7.
- Genta, G. (2005). Dynamics of Rotating Systems. Springer. ISBN 978-0-387-20936-4.
- Jeffcott, H. H. (1919). "The Lateral Vibration Loaded Shafts in the Neighborhood of a Whirling Speed. - The Effect of Want of Balance". Philosophical Magazine. 6. 37.
- Krämer, E. (1993). Dynamics of Rotors and Foundations. Springer-Verlag. ISBN 978-0-387-55725-0.
- Lalanne, M., Ferraris, G. (1998). Rotordynamics Prediction in Engineering, Second Edition. Wiley. ISBN 978-0-471-97288-4.
{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크) - Muszyńska, Agnieszka (2005). Rotordynamics. CRC Press. ISBN 978-0-8247-2399-6.
- Nelson, F. (June 2003). "A Brief History of Early Rotor Dynamics". Sound and Vibration.
- Nelson, F. (July 2007). "Rotordynamics without Equations". International Journal of COMADEM. 3. 10. ISSN 1363-7681.
- Nelson, F. (2011). An Introduction to Rotordynamics. Vol. SVM-19 [1].
{{cite book}}: 외부 링크 위치volume= - Lalanne, M., Ferraris, G. (1998). Rotordynamics Prediction in Engineering, Second Edition. Wiley. ISBN 978-0-471-97288-4.
{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크) - Vance, John M. (1988). Rotordynamics of Turbomachinery. Wiley. ISBN 978-0-471-80258-7.
- Tiwari, Rajiv (2017). Rotor Systems: Analysis and Identification. CRC Press. ISBN 9781138036284.
- Vance, John M., Murphy, B., Zeidan, F. (2010). Machinery Vibration and Rotordynamics. Wiley. ISBN 978-0-471-46213-2.
{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크) - Vollan, A., Komzsik, L. (2012). Computational Techniques of Rotor Dynamics with the Finite Element Method. CRC Press. ISBN 978-1-4398-4770-1.
{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크) - Yamamoto, T., Ishida, Y. (2001). Linear and Nonlinear Rotordynamics. Wiley. ISBN 978-0-471-18175-0.
{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크) - Ganeriwala, S, Mohsen N(2008). XLRotor를 사용한 Rotordynamic Analysis. SQI03-02800-0811
메모들
- ^ Liu, Shibing; Yang, Bingen (2017-02-22). "Vibrations of Flexible Multistage Rotor Systems Supported by Water-Lubricated Rubber Bearings". Journal of Vibration and Acoustics. 139 (2): 021016–021016–12. doi:10.1115/1.4035136. ISSN 1048-9002.
- ^ Myklestad, Nils (April 1944). "A New Method of Calculating Natural Modes of Uncoupled Bending Vibration of Airplane Wings and Other Types of Beams". Journal of the Aeronautical Sciences (Institute of the Aeronautical Sciences). 11 (2): 153–162. doi:10.2514/8.11116.
- ^ Prohl, M. A. (1945), "A General Method for Calculating Critical Speeds of Flexible Rotors", Trans ASME, 66: A–142
- ^ "ROTORDYNAMICS OF TURBOMACHINERY, Software and Engineering services, Alfa-Tranzit Co". www.alfatran.com. Retrieved 2022-01-11.
- ^ "AxSTREAM - Rotordynamics Turbomachinery Design Software". www.softinway.com. 2016-07-27. Retrieved 2022-01-11.
- ^ "Home". www.fem.unicamp.br. Retrieved 2022-01-11.
{{cite web}}: CS1 maint : url-status (링크) - ^ "Archived copy". Archived from the original on 2012-09-29. Retrieved 2013-06-04.
{{cite web}}: CS1 maint: 타이틀로 보관된 사본(링크) - ^ "Home". www.madyn.de. Retrieved 2022-01-11.
{{cite web}}: CS1 maint : url-status (링크) - ^ "MADYN 2000 for Rotordynamics". www.delta-js.ch. Retrieved 2022-01-11.
- ^ "Archived copy". Archived from the original on 2021-05-07. Retrieved 2022-01-11.
{{cite web}}: CS1 maint: 타이틀로 보관된 사본(링크) - ^ "FEMRDYN". dynatechengr.com. Retrieved 2022-01-11.
- ^ "Dyrobes – A Revolution in Rotor Dynamics Software". Retrieved 2022-01-11.
- ^ "Archived copy". Archived from the original on 2013-10-04. Retrieved 2013-10-01.
{{cite web}}: CS1 maint: 타이틀로 보관된 사본(링크) - ^ "Home". XLRotor. Retrieved 2022-01-11.
- ^ "Archived copy". Archived from the original on 2020-02-21. Retrieved 2022-01-11.
{{cite web}}: CS1 maint: 타이틀로 보관된 사본(링크) - ^ "Turbomachinery Laboratory". turbolab.tamu.edu. Retrieved 2022-01-11.
- ^ "Rotating Machinery and Controls Laboratory".
- ^ "the Szewalski Institute of Fluid-flow Machinery". Archived from the original on 2008-12-15.
- ^ "D&M; Technology Co., Ltd". Archived from the original on 2021-05-06.
- ^ "LaMCoS". lamcos.insa-lyon.fr. Retrieved 2022-01-11.
- ^ "Rotordynamics Software for Predictive Analyses of Rotating Machines". www.comsol.com. Retrieved 2022-01-11.
- ^ "Rotordynamics-Seal Research - RSR". rda.guru. Retrieved 2022-01-11.
{{cite web}}: CS1 maint : url-status (링크)

