지진 간섭계

Seismic interferometry

간섭계는 지표면에 대한 유용한 정보를 얻기 위해 신호 쌍 사이의 일반적인 간섭 현상을 조사한다.[1] 지진 간섭계(SI)는 신호 쌍의 교차 상관관계를 이용하여 주어진 매체의 충격 반응을 재구성한다. 케이이티 아키(1957),[2][3] 게자 쿠네츠, 존 클라르바우트(1968)의 논문들은 지진 응용에 대한 기법을 개발하는 데 도움을 주었으며, 현대 이론의 기초가 되는 틀을 제공했다.

위치 A의 신호는 위치 B의 신호와 교차 상관되어 지진 간섭계를 사용하여 가상 소스-수신기 쌍을 재현할 수 있다. 교차상관은 이 접근법에서 핵심 수학 연산으로 간주되는 경우가 많지만, 유사한 결과를 도출하기 위해 콘볼루션을 사용하는 것도 가능하다. 자유 표면에서 측정한 패시브 노이즈의 교차 상관성은 표면하 반응을 충동적인 포인트 선원에 의해 유도된 것처럼 재현하는데, 이는 정의상 그린의 기능과 동일한 것이다.[4] 이와 같이, 능동 지진원이 필요 없이 지표면에 관한 정보를 얻을 수 있다.[5] 그러나 이 방법은 패시브 소스에 국한되지 않으며 능동 소스와 컴퓨터 생성 파형에 사용할 수 있도록 확장할 수 있다.[1]

지표면 조사를 위한 지진파의 유용성을 보여주는 이미지

2006년 현재 지진 간섭 측정 분야는 지구 물리학자들이 지진 소음을 보는 방식을 바꾸기 시작하고 있었다. 내진 간섭계는 이전에 비점화된 이 배경파장을 사용하여 지표면의 모델을 역문제로 구성하는 데 사용할 수 있는 새로운 정보를 제공한다. 잠재적 적용 범위는 대륙 규모에서부터 훨씬 더 작은 규모의 자연 재해, 산업 및 환경 적용까지 다양하다.[1]

역사와 발전

클라르바우트(1968)는 지진 간섭계가 실제 세계 미디어에 적용될 수 있다는 것이 나중에 증명된 것은 아니지만, 기존의 간섭계 기법을 얕은 지표면 조사에 적용하기 위해 워크플로우를 개발했다.[1][6] 무작위 초음파 장기 평균은 알루미늄 블록의 두 지점 사이의 충격 반응을 재구성할 수 있다. 그러나, 그들은 무작위 확산 소음을 가정하여 실제 세계 조건에서의 간섭계측을 제한했다. 유사한 경우, 상관관계가 없는 소음원에 대한 표현은 두 수신기에서 관측치의 단일 교차 상관으로 감소하는 것으로 나타났다. 지표면의 대기권간 충격 반응은 처음에는 지표면과 직파 도달에 대해서만 배경 잡음의 확장된 기록만을 사용하여 재구성할 수 있다.[7][8]

지표면 또는 지표면의 능동 및 수동 발생원으로부터의 지진 신호의 교차 상관관계를 이용하여 지표면의 유효한 모델을 재구성할 수 있다.[9] 지진 간섭계는 파장 또는 주변 선원의 확산성에 제한 없이 전통적인 방법과 유사한 결과를 산출할 수 있다. 드릴링 애플리케이션에서는 가상 소스를 활용하여 다운홀 위치에 인접한 지표면을 이미지화할 수 있다. 이 애플리케이션은 특히 하위 살트의 환경 탐사에 점점 더 많이 활용되고 있다.[10]

수학적, 물리학적 설명

지진 간섭계는 두 지진 추적의 교차 관계를 이용하여 지표면 아래 반사 반응을 재구성할 수 있는 가능성을 제공한다.[1][5] 최근의 연구는[11] 무손실, 3D 이질적인 매체에서 파장 상호주의 정리를 이용하여 그린의 기능을 재구성하기 위한 교차상관 응용을 수학적으로 입증했다. 추적은 수동적 배경 소음의 확장된 기록이지만 목표에 따라 능동원을 활용할 수도 있다. 지진 간섭계는 기본적으로 인접 수신기 위치 사이의 위상 차이를 이용하여 지표면을 이미지화한다.

상관된 신호에서 그린의 기능을 회수한다는 의미인 방법이 유효하기 위한 조건이 다음과 같이 제시된다.[1][12]

  • 소스는 시간상 상관관계가 없다.
  • 선원은 표면파를 재구성하기 위해 수신기 주위로 위치한다.
  • 파장은 압축파와 전단파로 구성되는 장치다.

마지막 두 가지 조건은 자연에서 직접 만나기가 어렵다. 그러나 파동 산란 덕분에 파동이 변환되어 장비 조건을 만족시킨다. 파도가 사방으로 흩어진다는 사실 덕분에 균등한 공급원 분포가 충족된다.[12]

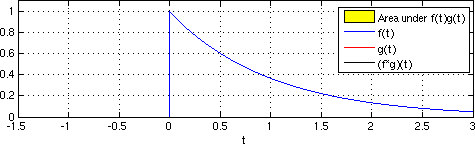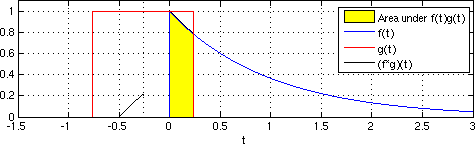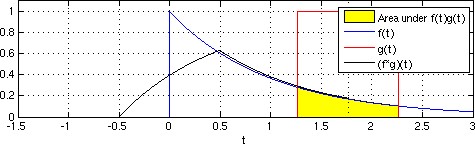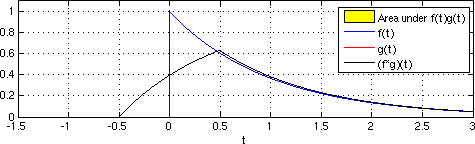
내진 간섭계는 실제 수신자 반응의 단순한 교차 상관과 적층 등으로 구성되어 있어 마치 가상의 선원을 해당 수신자의 위치에 배치한 것처럼 임펄스 반응에 근사하게 된다.[1] 시간영역에서 연속함수의 교차상관성은 방정식 1로 제시한다.

방정식 1

(f 1∗f 2)(t)= ∫ f 1(λ)f 2(λ-t)dλ

함수가 서로 다른 지연 값에서 시간의 함수로 통합되는 경우. 실제로 교차 상관은 두 개의 이산 수신기 위치의 파형과 관련된 이동 시간 지연으로 개념적으로 이해할 수 있다. 교차상관은 첫 번째 기능에 비해 두 번째 기능이 접히는 경련과 비슷하다.[13]

내진 간섭계는 강도가 주로 위상 구성요소에 의존하는 유리 렌즈를 통과하는 직사파 및 반사파의 간섭에 의해 생성된 광학 간섭그램과 근본적으로 유사하다.

콘볼루션의 원리. 교차 상관과 유사함

방정식 2

I = 1+2R2 cos[Ω(λAr+λrB)]+R^4

여기서: 강도는 반사 계수(R)와 위상 성분 Ω((Ar++rB)의 크기와 관련이 있다.[5][11] A가 기준 추적을 나타내는 위치 B에서 기록한 반사와 위치 A의 직파 교차 상관관계를 통해 반사율 분포의 추정을 얻을 수 있다.[9] A에서 추적 스펙트럼의 결합과 B에서 추적 스펙트럼의 곱은 다음을 제공한다.

방정식 3

фAB =Re^iΩ(λAr+λrB) + O.t.

여기서: фAB = 제품 스펙트럼 O.t. = 추가 용어(예: 직접 연결의 상관 관계 등)[clarification needed] 앞의 경우와 같이 제품 스펙트럼은 위상의 함수다.

키: 반사기 형상의 변경은 상관관계 결과의 변경으로 이어지고, 반사기 형상은 마이그레이션 커널의 적용을 통해 복구할 수 있다.[1][9] 원시 인터페로그램의 해석은 일반적으로 시도되지 않는다. 교차 상관관계 결과는 일반적으로 어떤 형태의 마이그레이션을 사용하여 처리된다.[9]

가장 간단한 경우 표면의 지오폰으로 기록된 에너지를 방사하는 깊이에서 회전 드릴 비트를 고려하십시오. 주어진 위치에서의 소스 파장의 위상이 무작위라고 가정할 수 있으며, 위치 B에 유령이 반사된 위치 A에서 직접 파동의 교차 상관관계를 이용하여 소스 위치에 관한 지식 없이 지표면 아래 반사체를 이미지화할 수 있다.[9] 주파수 영역에서 추적 A와 B의 교차 상관관계는 다음과 같이 단순화된다.

방정식 4

ф(A, B) = -(WiΩ)^2 Re^iΩ(λArλrB)+o.t.

위치: Wi(Ω) = 주파수 영역 소스 웨이브릿(ith wavelet)

위치 B에 귀신이 반사된 위치 A에서 직파 교차 상관관계는 다음과 같은 위치의 알려지지 않은 소스 용어를 제거한다.

방정식 5

ф(A,B)≈Re^iΩ(λArλrB)

이 양식은 위치 A에서 가상 소스 구성 위치 B에서 가상의 반사를 이미징하는 것과 동일하다. 이러한 상관 관계 위치의 마이그레이션은 단계 용어를 제거하고 위치 x에서 다음과 같은 위치에 최종 마이그레이션 이미지를 생성한다.

m(x) = σø(A,B,λAx+λxB) 여기서: ø(A,B,t) = 지연 시간이 t인 위치 A와 B 사이의 시간 상관 관계

이 모델은 서텍사스에서 전통적인 매립형 선원과 유사한 결과를 내기 위해 합성(가상) 회전 드릴 비트 선원을 포함한 시뮬레이션 모델을 사용하여 표면하 지오메트리를 시뮬레이션하는 데 적용되었다.[9][14] 유사한 모델은 모의실험된 표면하 기하학의 재구성을 입증했다.[5] 이 경우 재구성된 지표하 응답은 프라이머리와 배수의 상대적 위치를 정확하게 모델링했다. 광범위한 사례에서 신호 기하학적 구조를 재구성하기 위해 추가 방정식을 도출할 수 있다.

적용들

지진 간섭계는 현재 주로 연구와 학문적 환경에 활용되고 있다. 한 예에서는 수동 청취와 긴 소음 트레이스의 교차 상관 관계를 사용하여 캘리포니아 남부의 얕은 지표면 아래 속도 분석에 대한 충격 반응을 대략적으로 추정했다. 지진 간섭 측정은 정교한 반전 기법을 사용하여 표시된 결과와 비교 가능한 결과를 제공했다. 내진 간섭계는 가까운 표면의 검사에 가장 많이 사용되며 표면과 직파를 재구성하는 데만 사용된다. 이와 같이, 지진 간섭계는 일반적으로 그 제거에 도움이 되는 지면 롤을 추정하는 데 사용된다.[1] 내진 간섭계는 입석 건물의 전단파 속도 및 감쇠의 추정치를 단순화한다.[15] 지진계측법은 화산의 지진 산란과 속도 구조를 이미지화하기 위해 적용되었다.

지오폰에 의해 기록된 지진 표시

탐사 및 제작

지진 간섭계는 점점 더 탐험과 생산의 자리를 찾고 있다.[18] SI는 소금 돔에 인접한 침전물을 이미지화할 수 있다.[19] 복잡한 소금 기하학은 전통적인 내진 반사 기법을 사용하여 잘 해결되지 않는다. 대안적인 방법은 표면 아래 염분에 인접한 다운홀 선원과 수신기의 사용을 요구한다. 다운홀 위치에서 이상적인 지진 신호를 생성하기 어려운 경우가 많다.[18][19] 내진 간섭계는 소금 돔의 옆구리에 있는 가파르게 담그는 퇴적물을 더 잘 조명하고 포착하기 위해 사실상 소스를 아래쪽 구멍으로 이동시킬 수 있다. 이 경우 SI 결과는 실제 다운홀 소스를 사용하여 얻은 결과와 매우 유사했다. 내진 간섭계는 미지의 선원의 위치를 찾을 수 있으며 유도 골절의 정도를 매핑하기 위해 종종 하이드로프랙 어플리케이션에 사용된다.[9] 지표면 내 저장장치 성질의 미묘한 변화에 대한 시간 경과 내진 감시에 상호기하 기법을 적용할 수 있다.[1]

제한 사항

내진 간섭계 적용은 현재 여러 요인에 의해 제한되어 있다. 현실 세계 미디어와 소음은 현재의 이론적 발전을 위한 한계를 나타낸다. 예를 들어 간섭계측에서 작동하려면 소음원은 상관관계가 없어야 하며 관심 영역을 완전히 둘러싸야 한다. 또한 감쇠와 기하학적 확산은 크게 방치되고 있으며 보다 강력한 모델에 통합될 필요가 있다.[1] 다른 도전들은 지진 간섭계에 내재되어 있다. 예를 들어 위치 B에 귀신이 반사된 위치 A에서 직접 파동이 교차하는 경우 소스 용어는 제외된다. 다른 파형의 상관관계는 결과적인 인터페로그램에 배수를 도입할 수 있다. 속도 분석 및 필터링은 주어진 데이터 집합에서 배수의 발생을 감소시키지만 제거하지는 못한다.[9]

비록 지진 간섭계 도전에 많은 진전이 있었지만 여전히 남아있다. 남은 가장 큰 과제 중 하나는 이론의 확장을 실제 세계 미디어와 지하의 소음 분포를 설명하도록 하는 것이다. 자연원은 일반적으로 수학적 일반화를 따르지 않으며 실제로 어느 정도의 상관관계를 나타낼 수 있다.[1] 지진 간섭계 적용이 더 널리 확산되기 전에 추가 문제를 해결해야 한다.

메모들

  1. ^ a b c d e f g h i j k l 커티스 외 2006년
  2. ^ Aki, Keiiti (1957). "Space and time spectra of stationary stochastic waves, with special reference to microtremors". Bulletin of the Earthquake Research Institute. 35: 415–457. hdl:2261/11892.
  3. ^ Claerbout, Jon F. (April 1968). "Synthesis of a Layered Medium from ITS Acoustic Transmission Response". Geophysics. 33 (2): 264–269. Bibcode:1968Geop...33..264C. doi:10.1190/1.1439927.
  4. ^ Snieder, Roel; Wapenaar, Kees (2010-09-01). "Imaging with ambient noise". Physics Today. 63 (9): 44–49. Bibcode:2010PhT....63i..44S. doi:10.1063/1.3490500. ISSN 0031-9228.
  5. ^ a b c d 드라고노프, 와페나르 & 토르베케 2006
  6. ^ 위버 & 로비스 2001
  7. ^ 와페나르 2004
  8. ^ 캄필로 & 폴 2003
  9. ^ a b c d e f g h 슈스터 외 2004
  10. ^ Bakulin & Calvert 2004
  11. ^ a b 와페나르 & 포케마 2006
  12. ^ a b Larose, Eric; Carrière, Simon; Voisin, Christophe; Bottelin, Pierre; Baillet, Laurent; Guéguen, Philippe; Walter, Fabian; Jongmans, Denis; Guillier, Bertrand; Garambois, Stéphane; Gimbert, Florent (2015-05-01). "Environmental seismology: What can we learn on earth surface processes with ambient noise?". Journal of Applied Geophysics. 116: 62–74. Bibcode:2015JAG...116...62L. doi:10.1016/j.jappgeo.2015.02.001. ISSN 0926-9851.
  13. ^ 애니메이션
  14. ^ Yu, Followill & Schuster 2003
  15. ^ Sneder & Safak
  16. ^ 채푸트 외, 2012년
  17. ^ 브렌지에 외 2007년
  18. ^ a b 혼비 & 유 2007
  19. ^ a b 루 외 2006년

참조