스트라러 수

수학에서, 스트라러 수(Strahler number) 또는 호튼-스트라 수(Horton-Strahler number)는 분기의 복잡도를 나타내는 수치이다.

이 숫자들은 로버트 E에 의해 수문학에서 처음 개발되었다. Horton(1945년) 및 Arthur Newell Strahler(1952년, 1957년)는 이 응용 프로그램에서는 Strahler 스트림 오더로 불리며 지류의 계층을 기반으로 스트림 크기를 정의하는 데 사용됩니다.또한 L-시스템 및 (생물) 나무, 동물 호흡 및 순환 시스템 등의 계층적 생물학적 구조 분석, 고급 프로그래밍 언어 컴파일을 위한 레지스터 할당 및 소셜 네트워크 분석에서 발생한다.대체 스트림 순서 시스템은 Shreve와^[1][2] Hodgkinson ^[3]등에 의해 개발되었다.스트림/링크 길이 분석과 함께 Strahler 및 Shreve 시스템의 통계적 비교가 ^[4]Smart에 의해 제공됩니다.

정의.

이 컨텍스트의 모든 트리는 루트에서 잎으로 향하는 방향 그래프입니다. 즉, 나무 모양입니다.트리의 노드 정도는 단지 자식 수일 뿐입니다.다음과 같이 트리의 모든 노드에 상향순으로 스트라 번호를 할당할 수 있습니다.

• 노드가 리프(자식이 없음)인 경우 해당 스트라 번호는 1입니다.
• 노드에 스트라 번호 i를 가진 아이가 1명 있고 다른 모든 자녀가 스트라 번호 i보다 작은 스트라 번호를 가진 경우 노드의 스트라 번호는 다시 i가 됩니다.
• 노드에 스트라 번호i의 자녀가 2명 이상 있고 그 수가 더 큰 자녀가 없는 경우 노드의 스트라 번호는 i + 1이 됩니다.

트리의 스트라 번호는 루트 노드의 번호입니다.

알고리즘적으로 이러한 번호는 깊이 우선 검색을 수행하고 각 노드의 번호를 후순으로 할당함으로써 할당될 수 있습니다.또한 동일한 숫자는 일련의 단계에서 트리가 단순화된 프루닝 프로세스를 통해 생성될 수 있으며, 각 단계에서 1개의 리프 노드와 리프(leaf)로 이어지는 모든 도수 1개의 노드 경로를 제거합니다. 노드의 스트라흘러 번호는 이 프로세스에 의해 제거되는 단계이며, 트리 i의 스트라흘러 번호는 스트라 번호입니다.모든 노드를 삭제하는 데 필요한 단계 수입니다.트리의 스트라러 수에 대한 또 다른 동등한 정의는 주어진 트리에 동형적으로 삽입될 수 있는 가장 큰 완전한 이진 트리의 높이입니다. 트리의 노드의 스트라러 수는 마찬가지로 노드 아래에 삽입될 수 있는 가장 큰 완전한 이진 트리의 높이입니다.

스트라흘러 번호가 i인 노드는 스트라흘러 번호가 i - 1인 최소 2개의 하위 항목, 스트라흘러 번호가 i - 2인 최소 4개의 하위 항목 및 최소^{i − 1} 2개의 리프 하위 항목이 있어야 합니다.따라서 n개의 노드를 가진 트리에서 가능한 최대 스트라 수는 log n + ^[5]1입니다₂.그러나 트리가 완전한 이진 트리를 형성하지 않는 한 스트라 수는 이 바인딩보다 작습니다.가능한 모든 이진 트리 중에서 균일하게 랜덤으로 선택되는 n-노드 이진 트리에서, 루트의 예상 지수는 ^[6]로그 n에 매우₄ 가까운 높은 확률로 선택됩니다.

적용들

하천망

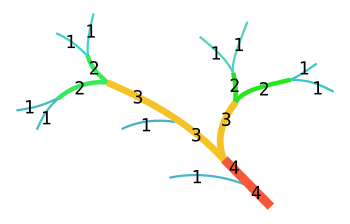
스트라흘러 하천 순서를 수문학에 적용할 때 하천 네트워크 내의 하천 또는 하천의 각 세그먼트는 트리 내의 노드로 취급되고 다음 세그먼트는 부모로 취급된다.2개의 1차 스트림이 결합하면 2차 스트림이 형성됩니다.2차 스트림이 결합되면 3차 스트림이 형성됩니다.상위 스트림에 참여하는 하위 스트림은 상위 스트림의 순서를 변경하지 않습니다.따라서 1차 스트림이 2차 스트림에 가입해도 2차 스트림으로 남습니다.2차 스트림이 다른 2차 스트림과 결합할 때까지 3차 스트림이 되지 않습니다.수학적 트리와 마찬가지로 지수 i를 가진 세그먼트는 지수 1의 적어도^{i − 1} 2개의 다른 지류에 의해 공급되어야 한다.Shreve는 Horton's와 Strahler's의 법칙은 위상적으로 랜덤한 분포에서 예상되어야 한다고 지적했다.그 후의 관계 재검토에 의해, 이 주장이 확인되어, 법이 기술하는 속성으로부터 ^[3][7]스트림 네트워크의 구조나 기원을 설명하는 결론을 도출할 수 없다는 것이 판명되었습니다.

하천의 자격을 얻으려면 수문학적 특징이 반복적이거나 영구적이어야 한다.반복(또는 "간헐적") 스트림은 적어도 1년 중 일부 동안 수로에 물이 있습니다.하천 또는 강의 지수는 1(지류가 없는 하천)에서 12(지구적으로 가장 강력한 강인 아마존 강)까지 다양합니다.오하이오강은 8등급이고 미시시피강은 10등급이다.지구상 하천의 80%가 1~3급 헤드워터 ^[8]스트림인 것으로 추정됩니다.

하천 네트워크의 분기 비율이 낮으면 높은 분기 비율이 나타나듯이 물이 분산되지 않고 하나의 수로에 집중되기 때문에 홍수가 발생할 가능성이 높다.분기율은 배수지의 어떤 부분이 범람할 가능성이 높은지도 개별 비율을 통해 확인할 수 있다.대부분의 영국 강은 3에서 ^[9]5 사이의 분기율을 가지고 있다.

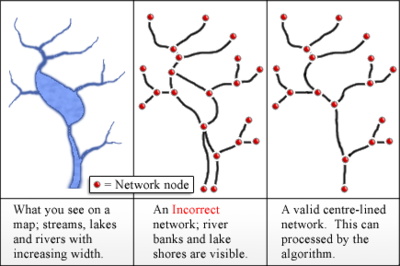
글리저 외 (2004)는 GIS 애플리케이션에서 Strahler 스트림 순서 값을 계산하는 방법을 설명합니다.이 알고리즘은 ESRI ArcGIS 10.7 툴인 RivEX에 의해 구현됩니다.이들의 알고리즘에 대한 입력은 수역의 중심선 네트워크로, 노드에서 결합된 호(또는 가장자리)로 표현된다.호수 경계와 강둑은 일반적으로 잘못된 토폴로지를 가진 비트리 네트워크를 형성하기 때문에 호수로 사용하지 마십시오.

기타 계층 시스템

스트라흘러 번호는 하천뿐만 아니라 모든 계층 시스템의 통계 분석에 적용할 수 있다.

• 아레나스 등 (2004)는 소셜 네트워크 분석에서 Horton-Strahler 지수의 적용을 설명한다.
• Ehrenfeucht, Rozenberg & Vermeir(1981)는 나무 순위라고 부르는 스트라 번호 부여의 변형을 L-시스템 분석에 적용했다.
• 스트라흘러 번호는 나무와^[10] 동물 호흡 ^[11]및 순환 시스템의 분기 구조와 같은 생물학적 계층 구조에도 적용되었다.

레지스터 할당

고급 프로그래밍 언어를 어셈블리 언어로 변환할 때 식 트리를 평가하는 데 필요한 최소 레지스터 수는 스트라 번호입니다.이 문맥에서 스트라 번호는 레지스터 ^[12]번호라고도 불립니다.

사용 가능한 수보다 많은 레지스터를 필요로 하는 표현 트리의 경우, Sethi-Ullman 알고리즘을 사용하여 표현 트리를 가능한 한 효율적으로 레지스터를 사용하는 일련의 기계 명령으로 변환할 수 있으며, 레지스터에서 메인 메모리로 중간 값이 유출되는 횟수와 i의 총 수를 최소화할 수 있습니다.nstructions가 컴파일된 코드에 포함되어 있습니다.

관련 파라미터

분기비

트리의 스트라흘러 숫자와 관련된 것은 분기 비율이며, 이는 트리의 균형에 얼마나 가까운지를 나타내는 수치입니다.계층 내 각 차수 i에 대해 ih 분기율은 다음과 같다.

$({displaystyle {n_{i}}{n_{i+1}}})$

여기서_i n은 순서가 i인 노드의 수를 나타냅니다.

전체 계층의 분기 비율은 서로 다른 순서로 분기 비율을 평균하여 얻을 수 있습니다.완전한 이진 트리에서 분기 비율은 2이지만 다른 트리의 분기 비율은 더 커집니다.차원이 없는 숫자입니다.

패스폭

임의의 무방향 그래프 G의 패스폭은 서브그래프로 G를 포함하는 구간 그래프 H가 존재하도록 최소 수 w로 정의할 수 있으며, H에서 가장 큰 그룹에는 + 1의 정점이 있다.트리의 경우(방향과 루트를 잊어버려 무방향 그래프로 표시됨) 경로 폭은 스트라 번호와는 다르지만 밀접한 관련이 있다. 경로 폭 w와 스트라 번호 s를 가진 트리에서 이 두 숫자는 부등식에^[13] 의해 관련된다.

w 2 2w + 2

트리가 아닌 주기가 있는 그래프를 처리할 수 있으므로 스트라러 숫자에 비해 경로 폭이 더 다양합니다.단, 스트라 숫자와 달리 경로 폭은 그래프 전체에 대해서만 정의되며 그래프 내의 각 노드에 대해서는 별도로 정의되지 않습니다.

「 」를 참조해 주세요.

• 강의 주요 줄기로, 일반적으로 스트라흘러 수가 가장 높은 분지를 따라가면 발견됩니다.
• Pfafstetter 부호화 시스템

메모들

레퍼런스

• 를 클릭합니다Arenas, A.; Danon, L.; Díaz-Guilera, A.; Gleiser, P. M.; Guimerá, R. (2004), "Community analysis in social networks", European Physical Journal B, 38 (2): 373–380, arXiv:cond-mat/0312040, Bibcode:2004EPJB...38..373A, doi:10.1140/epjb/e2004-00130-1, S2CID 9764926.
• 를 클릭합니다Borchert, Rolf; Slade, Norman A. (1981), "Bifurcation ratios and the adaptive geometry of trees", Botanical Gazette, 142 (3): 394–401, doi:10.1086/337238, hdl:1808/9253, JSTOR 2474363, S2CID 84145477.
• 를 클릭합니다Devroye, Luc; Kruszewski, Paul (1995), "A note on the Horton–Strahler number for random trees", Information Processing Letters, 56 (2): 95–99, doi:10.1016/0020-0190(95)00114-R.
• Devroye, L.; Kruszewski, P. (1996), "On the Horton–Strahler number for random tries", RAIRO Informatique Théorique et Applications, 30 (5): 443–456, doi:10.1051/ita/1996300504431, MR 1435732
• 를 클릭합니다Ehrenfeucht, A.; Rozenberg, G.; Vermeir, D. (1981), "On ETOL systems with finite tree-rank", SIAM Journal on Computing, 10 (1): 40–58, doi:10.1137/0210004, MR 0605602.
• 를 클릭합니다Ershov, A. P. (1958), "On programming of arithmetic operations", Communications of the ACM, 1 (8): 3–6, doi:10.1145/368892.368907, S2CID 15986378.
• 를 클릭합니다Flajolet, P.; Raoult, J. C.; Vuillemin, J. (1979), "The number of registers required for evaluating arithmetic expressions", Theoretical Computer Science, 9 (1): 99–125, doi:10.1016/0304-3975(79)90009-4.
• 를 클릭합니다Gleyzer, A.; Denisyuk, M.; Rimmer, A.; Salingar, Y. (2004), "A fast recursive GIS algorithm for computing Strahler stream order in braided and nonbraided networks", Journal of the American Water Resources Association, 40 (4): 937–946, Bibcode:2004JAWRA..40..937G, doi:10.1111/j.1752-1688.2004.tb01057.x.
• 를 클릭합니다Horsfield, Keith (1976), "Some mathematical properties of branching trees with application to the respiratory system", Bulletin of Mathematical Biology, 38 (3): 305–315, doi:10.1007/BF02459562, PMID 1268383, S2CID 189888885.
• 를 클릭합니다Horton, R. E. (1945), "Erosional development of streams and their drainage basins: hydro-physical approach to quantitative morphology", Geological Society of America Bulletin, 56 (3): 275–370, doi:10.1130/0016-7606(1945)56[275:EDOSAT]2.0.CO;2.
• 를 클릭합니다Lanfear, K. J. (1990), "A fast algorithm for automatically computing Strahler stream order", Journal of the American Water Resources Association, 26 (6): 977–981, Bibcode:1990JAWRA..26..977L, doi:10.1111/j.1752-1688.1990.tb01432.x.
• Luttenberger, Michael; Schlund, Maxmilian (2011), An extension of Parikh's theorem beyond idempotence, arXiv:1112.2864, Bibcode:2011arXiv1112.2864L
• 를 클릭합니다Strahler, A. N. (1952), "Hypsometric (area-altitude) analysis of erosional topology", Geological Society of America Bulletin, 63 (11): 1117–1142, doi:10.1130/0016-7606(1952)63[1117:HAAOET]2.0.CO;2.
• 를 클릭합니다Strahler, A. N. (1957), "Quantitative analysis of watershed geomorphology", Transactions of the American Geophysical Union, 38 (6): 913–920, Bibcode:1957TrAGU..38..913S, doi:10.1029/tr038i006p00913.
• 를 클릭합니다Waugh, David (2002), Geography, An Integrated Approach (3rd ed.), Nelson Thornes.