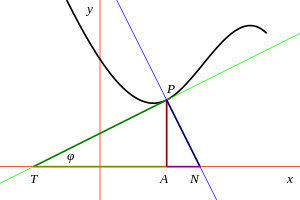
주어진 점 P에서 곡선(검은색)에 대한 하위 및 관련 개념.접선과 정규선은 각각 녹색과 파란색으로 표시된다.표시된 거리는 세로좌표(AP), 접선(TP), 중간(TA), 정규(PN), 하위 정규(AN)이다.각도 φ은 접선선 또는 접선 각도의 경사각이다. 기하학에서, 하위 절 및 관련 항은 주어진 점의 곡선과 좌표 축에 접하는 선을 사용하여 정의된 특정 선 세그먼트다.이 용어는 오늘날 다소 구식이지만 20세기 초반까지 널리 쓰였다.
정의들
P = (x, y)를 주어진 곡선의 점으로 하고 A = (x, 0) X 축에 투영한다.P에서 곡선에 접선을 그리고 이 선이 X축을 교차하는 점이 T가 되게 한다.그런 다음 TA는 P에서 하위 합계로 정의된다.마찬가지로, P에서 곡선과 정규 분포를 이루는 것이 N에서 X축을 교차하는 경우, A를 부정규격이라고 한다.이 맥락에서 PT와 PN의 길이를 접선 및 정규라고 하며, 접선 및 정규선이라고도 하는 정규선과 혼동하지 않는다.
방정식
X축에 대한 접선의 기울기 각도가 되도록 한다. 이것을 접선각이라고도 한다.그러면

그래서 하위 계수는

그리고 그 이하의 보통은

보통은 에 의해 주어진다.

그리고 접선은 다음에 의해 주어진다.

극 정의

주어진 점 P에서 곡선(검은색)에 대한 극소량 및 관련 개념.접선과 정규선은 각각 녹색과 파란색으로 표시된다.표시된 거리는 반경(OP), 극소량(OT), 극소수(ON)이다.각도 θ은 반경 또는 극 접선 각도에 대한 접선의 기울기의 반경 각도 ψ이다. P = (r, θ)를 극좌표에 의해 정의된 주어진 곡선의 점으로 하고 O를 원점을 나타내도록 한다.OP에 수직인 O를 통해 선을 그리고 이제 이 선이 P에서 곡선과 접선을 교차하는 지점이 되도록 한다.마찬가지로, 이제 N은 곡선에 대한 정규 분포가 선과 교차하는 점이 되도록 한다.그 다음 OT와 ON은 각각 P에서 곡선의 극소량 및 극소수 정규라고 한다.
극 방정식
ψ 탄젠트와 레이 OP 사이의 각도로 하자; 이것을 극 탄젠트 각도라고도 한다.그러면

그래서 극소량(polar subangent가

그리고 그 이하의 보통은

참조
- B. Williamson의 미분학(1899) 페이지 215, 223 인터넷 아카이브에 대한 기초 논문에서 "하위 및 하위 정규"와 "극하위 및 극하위 정규"












